【Python学习笔记】类型/运算/变量/注释
前言
人生苦短,追求生产力,做一只时代风口的猪,应该学python
Python语言中,所有的数据都被称之为对象。
1. 对象类型
Python语言中,常用的数据类型有:
-
整数, 比如 3
-
小数(也叫浮点数) ,比如 6.5
-
字符串 , 比如 ‘你好’
-
列表,比如 [1, 2, ‘你好’]
-
元组,比如 (1, 2, ‘你好’)
-
字典,比如 {1:‘mike’, 2:‘jack’}
2. 常见数学运算
-
加法
>>> 5 + 8 13
-
减法
>>> 999 - 111 888
-
乘法
>>> 8 * 9 72
-
除法
>>> 3 / 2 1.5 #注意,计算结果是小数
-
求商
>>> 3 // 2 1
-
求余
>>> 3 % 2 1
-
次方
>>> 10 ** 3 1000
3. type 函数
Python解释器 内置了 type函数,可以用来查看数据对象的类型。比如
>>> type(1)
<class 'int'> # int类型
>>> type(3.4)
<class'float'> # float类型
>>> type("222")
<class 'str'> # 字符串类型
4. 变量及命名规则
没有被引用的对象,解释器会在随后某个时候从内存中清除掉。变量名不是随便取的,有一定的规则。
-
变量名可以包含 字母、数字和下划线。
-
变量名可以以字母或下划线打头,比如 var1 , 或者 _var
-
但不能以数字打头, 像 1var 这样是不行的
-
变量名中不能包含空格
-
变量名中可以包含下划线,像下面这样都是可以的
-
Hello, var1, age2name, age_name
-
变量名 不能 和 关键字 同名
-
变量名 不要 和 内置函数 同名
5. 特别要注意的是,有如下两种变化情况
1) 变量 重新指向了 新的对象
kid = '小明'
student = kid
prettyboy = kid
print(kid)
print(student)
print(prettyboy)
print("\r\n\r\n");
kid = "小周"
print(kid)
print(student)
print(prettyboy)
运行结果
D:\>python main.py 小明 小明 小明小周 小明 小明
说明:这只会改变 kid 一个变量和其指向对象的关系,并不会改变其他的变量名 student 和 prettyboy,先后两次的对应关系如下:
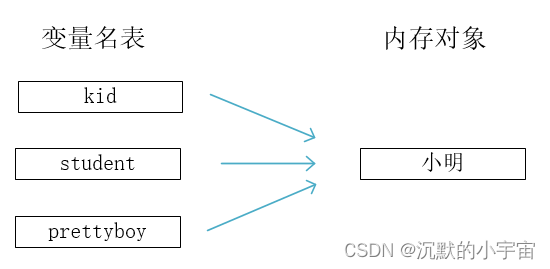
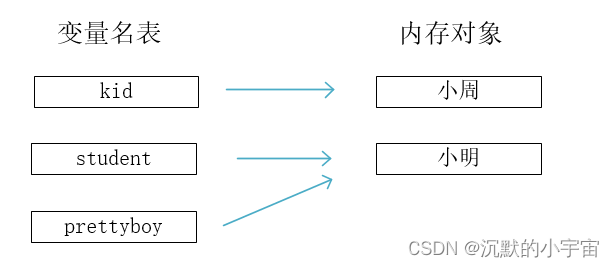
2)变量指向的对象本身发生了变化
这种情况,是当变量指向的对象是可变的数据类型 ,比如:列表、字典,或者自定义的类实例对象。例如:
info = {'name' :'user', 'height':'180cm'}
info['height'] = '175cm'
print(info)
运行结果:
D:\>python main.py
{'name': 'user', 'height': '175cm'}
第二条语句就是让变量对应的字典对象的值发生了变动
6. 注释
单行注释:以 # 开头,后面的内容都是注释
多行注释:("""被注释的内容""")('''被注释的内容''')
By Urien 2023.10.13
相关文章:

【Python学习笔记】类型/运算/变量/注释
前言 人生苦短,追求生产力,做一只时代风口的猪,应该学python Python语言中,所有的数据都被称之为对象。 1. 对象类型 Python语言中,常用的数据类型有: 整数, 比如 3 小数(也叫浮…...
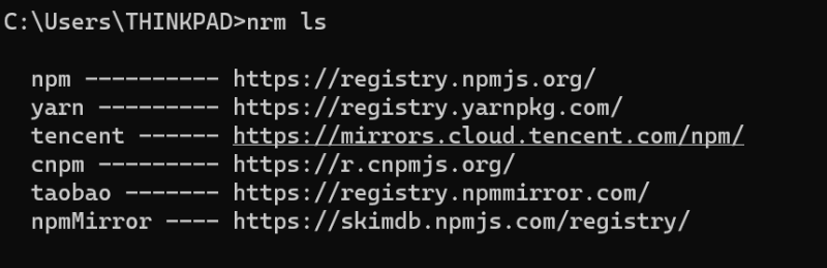
国内常用源开发环境换源(flutter换源,python换源,Linux换源,npm换源)
flutter换源 使用环境变量:PUB_HOSTED_URL FLUTTER_STORAGE_BASE_URL, upgrade出问题时可能会提示设置FLUTTER_GIT_URL变量。 flutter中国 PUB_HOSTED_URLhttps://pub.flutter-io.cn FLUTTER_STORAGE_BASE_URLhttps://storage.flutter-io.cn FLUTTER_GIT_URLhtt…...
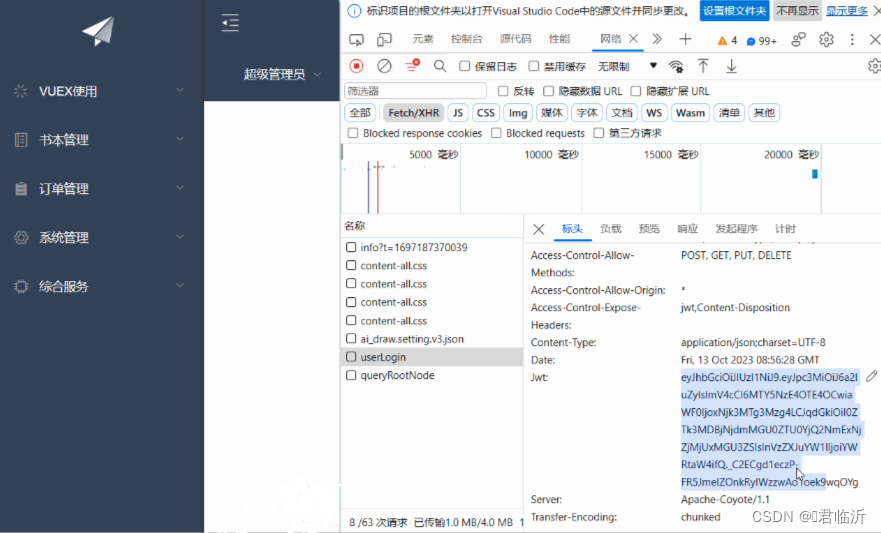
关于一篇什么是JWT的原理与实际应用
目录 一.介绍 1.1.什么是JWT 二.结构 三.Jwt的工具类的使用 3.1. 依赖 3.2.工具类 3.3.过滤器 3.4.控制器 3.5.配置 3.6. 测试类 用于生成JWT 解析Jwt 复制jwt,并延时30分钟 测试JWT的有效时间 测试过期JWT的解析 四.应用 今天就到这了,希…...

【Method】把 arXiv论文 转换为 HTML5 网页
文章目录 MethodReference https://ar5iv.labs.arxiv.org/ Articles from arXiv.org as responsive HTML5 web pages. 可以将来自 arXiv 的 PDF 论文渲染成 HTML5 网页版本。 Method View any arXiv article URL by changing the X to a 5. 将 arXiv 网址中的 x 换成 5 再回…...

每日一题AC
4.小花和小草正在沙滩上玩挖沙洞的游戏。他们划了一条长度为n米的线作为挖沙洞的参考线路,小花和小草分别从两头开始沿着划好的线开始挖洞,小花每隔a米挖一个洞,小草每隔b米挖一个洞,碰到已经挖过洞的就不需要再挖了。那么&#x…...
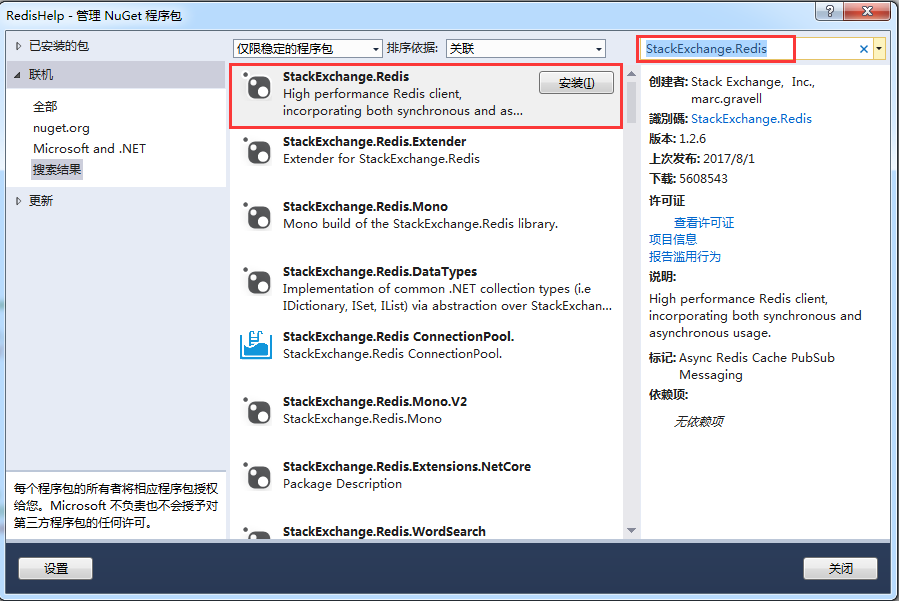
后端:推荐 2 个 .NET 操作的 Redis 客户端类库
目录 Redis特点 Redis场景 1. StackExchange.Redis 2. FreeRedis 🚀 快速入门 🎣 Master-Slave (读写分离) 💻 Pipeline (管道)示例 🌌 Redis Cluster (集群) Redis ,是一个高性能(NOSQL)的key-value数据库,Re…...

华泰证券:京东营收增长或短期承压
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,华泰证券近期发布研报称京东营收增长或短期承压。华泰证券主要观点如下:营收增长或短期承压,聚焦长期内生能力建设 考虑到消费情绪的恢复仍需一定时间,我们预计…...
Java从resources文件下载文档,文档没有后缀名
业务场景:因为公司会对excel文档加密,通过svn或者git上传代码也会对文档进行加密,所以这里将文档后缀去了,这样避免文档加密。 实现思路:将文档去掉后缀,放入resources下,获取输入流࿰…...

【动手学深度学习-Pytorch版】BERT预测系列——BERTModel
本小节主要实现了以下几部分内容: 从一个句子中提取BERT输入序列以及相对的segments段落索引(因为BERT支持输入两个句子)BERT使用的是Transformer的Encoder部分,所以需要需要使用Encoder进行前向传播:输出的特征等于词…...

Python之元组、字典和集合练习
1、餐厅下午茶 (列表与元组 crr66) 某餐厅推出了优惠下午茶套餐活动。顾客可以以优惠的价格从给定的糕点和给定的饮 料中各选一款组成套餐。已知,指定的糕点包括松饼(Muffins)、提拉米苏(Tiramisu)、芝士蛋 糕(Cheese Cake)和三明治(Sandwic…...
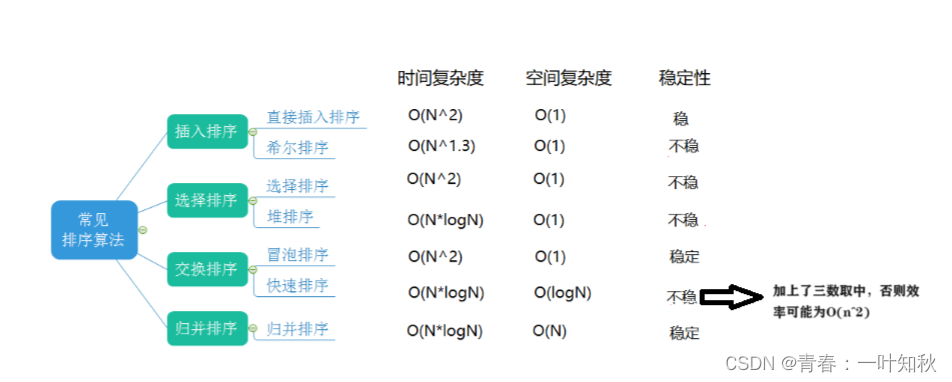
【数据结构】归并排序和计数排序(排序的总结)
目录 一,归并排序的递归 二,归并排序的非递归 三,计数排序 四,排序算法的综合分析 一,归并排序的递归 基本思想: 归并采用的是分治思想,是分治法的一个经典的运用。该算法先将原数据进行拆…...

某医疗机构:建立S-SDLC安全开发流程,保障医疗前沿科技应用高质量发展
某医疗机构是头部资本集团旗下专注大健康领域战略性投资与运营的实业公司,市场规模超300亿。该医疗机构已完成数字赋能,形成了标准化、专业化、数字化的疾病和健康管理体系,将进一步规划战略方向,为人工智能纳米技术、高温超导、生…...

验证二叉搜索树的后序遍历序列
LCR 152. 验证二叉搜索树的后序遍历序列 class VerifyTreeOrder:"""LCR 152. 验证二叉搜索树的后序遍历序列https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/description/"""def solution(self, postorder: Lis…...
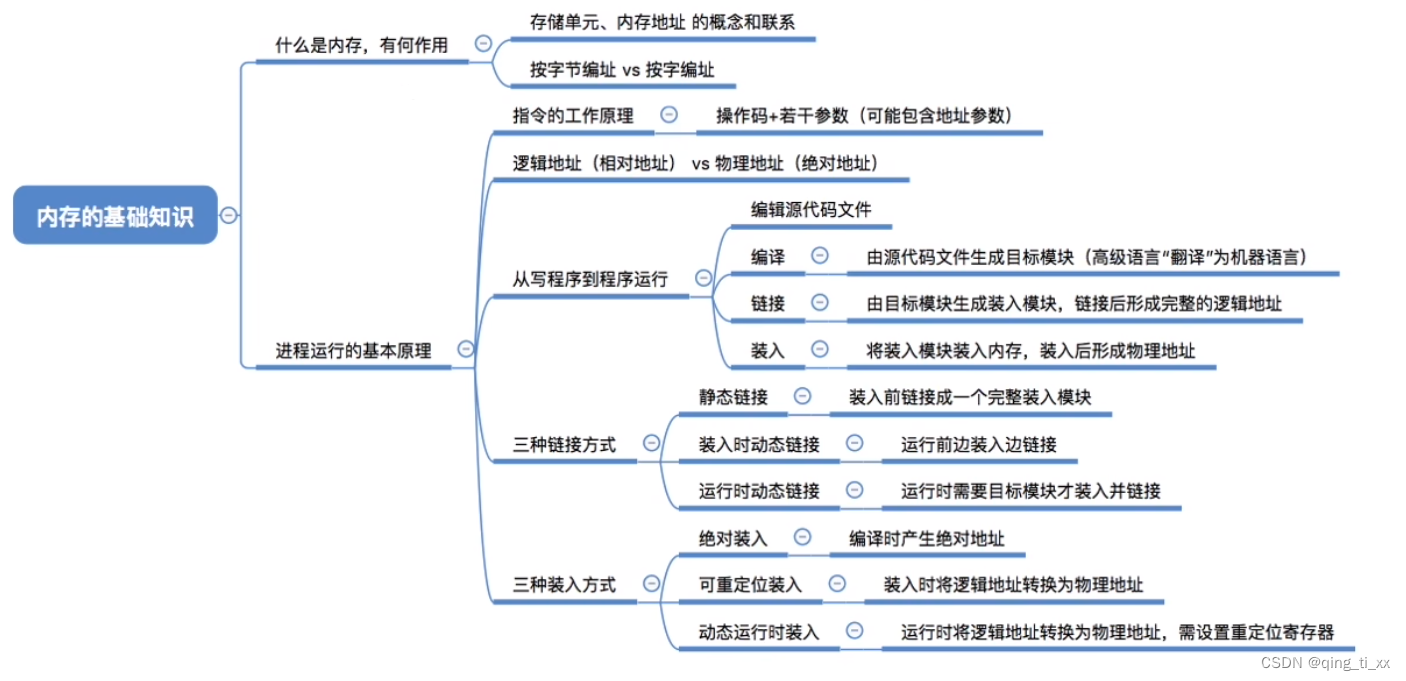
第三章 内存管理 一、内存的基础知识
目录 一、什么是内存 二、有何作用 三、常用数量单位 四、指令的工作原理 五、装入方式 1、绝对装入 2、可重定位装入(静态重定位) 3、动态运行时装入(动态重定位) 六、从写程序到程序运行 七、链接的三种方式 1、静态…...

【Java学习之道】Java常用集合框架
引言 在Java中,集合框架是一个非常重要的概念。它提供了一种方式,让你可以方便地存储和操作数据。Java中的集合框架包括各种集合类和接口,这些类和接口提供了不同的功能和特性。通过学习和掌握Java的集合框架,你可以更好地管理和…...
logicFlow 流程图编辑工具使用及开源地址
一、工具介绍 LogicFlow 是一款流程图编辑框架,提供了一系列流程图交互、编辑所必需的功能和灵活的节点自定义、插件等拓展机制。LogicFlow 支持前端研发自定义开发各种逻辑编排场景,如流程图、ER 图、BPMN 流程等。在工作审批配置、机器人逻辑编排、无…...
/OPTEE之动态代码分析汇总)
ATF(TF-A)/OPTEE之动态代码分析汇总
安全之安全(security)博客目录导读 1、ASAN(AddressSanitizer)地址消毒动态代码分析 2、ATF(TF-A)之UBSAN动态代码分析 3、OPTEE之KASAN地址消毒动态代码分析...

10-11 周三 shell xargs tr curl 做大事情
最近发现,shell的小工具非常的强大,简单记录下 tr命令 -d 删除字符串1中所有输入字符。-s 删除所有重复出现字符序列,只保留第一个;即将重复出现字符串压缩为一个字符串 -d 用于删除查询到的字符串中的空格。 [test3NH-DC-NM1…...

1.1 向量与线性组合
一、向量的基础知识 两个独立的数字 v 1 v_1 v1 和 v 2 v_2 v2,将它们配对可以产生一个二维向量 v \boldsymbol{v} v: 列向量 v v [ v 1 v 2 ] v 1 v 的第一个分量 v 2 v 的第二个分量 \textbf{列向量}\,\boldsymbol v\kern 10pt\boldsymbol …...

django: You may need to add ‘localhost‘ to ALLOWED_HOSTS
参考:https://blog.csdn.net/qq_21744873/article/details/87857279 python manage.py runserver后页面访问失败,提示: DisallowedHost at /admin/ Invalid HTTP_HOST header: ‘localhost:8000’. You may need to add ‘localhost’ to ALLOWED_HOSTS…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
