当前位置： 首页 > news >正文

《进化优化》第4章 遗传算法的数学模型

news 文章来源：https://blog.csdn.net/qq_45823731/article/details/133805278 2025/5/6 19:27:30

文章目录

  • 4.1 图式理论
  • 4.2 马尔可夫链
  • 4.3 进化算法的马尔可夫模型的符号
  • 4.4 遗传算法的马尔可夫模型
    • 4.4.1 选择
    • 4.4.2 变异
    • 4.4.3 交叉
  • 4.5 遗传算法的动态系统模型
    • 4.5.1 选择
    • 4.5.2 变异
    • 4.5.3 交叉

4.1 图式理论

  • 图式是描述一组个体的位模式，其中用*来表示不在乎的位。
  • 长度为l的图式总共有3^l种。
  • 长度为l的位串属于2^l个图式。
  • 在一个图式中有定义的位的个数称为此图式的阶，记为o。
  • 在图式中从最左边的定义位到最右边定义位的位的个数称为定义长度.
  • 属于某个图示的一个位串称为此图式的一个实例。
  • 一般来说，一个图式含有的实例个数等于2^A，这里A是图式中星号的个数。
  • 平均适应度：

在这里插入图片描述

  • 第t+1代实例个数的期望等于适应度总和/平均适应度
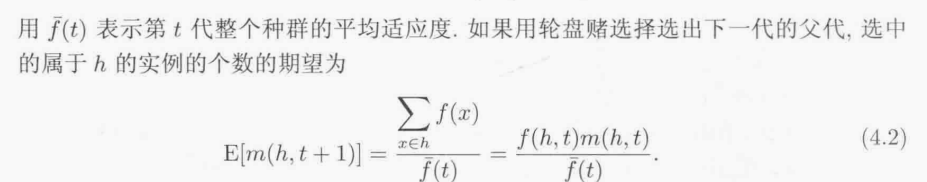
    在这里插入图片描述
    交叉破坏图式的概率：
  • 考虑图式h =1****.交叉不会破环这个图式.如果这个图式的一个实例与另一个位串交叉,至少会有一个子代仍是h的实例.
  • 考虑图式h=11***.如果这个图式的一个实例与位串x交叉,交叉点可以有4个位置.如果交叉点在两个1位之间,图式可能会被破坏,它取决于x的值.如果交叉点在右边(另外三个可能的交叉点),图式就不会被破坏;至少有一个子代会是h的实例.由此可见,图式被破坏的概率小于或等于1/4,它取决于交叉发生的位置.
  • 考虑图式h =1*1**.如果这个图式的一个实例与位串c交叉,则交叉点可以是4个位置中的其中一个.如果交叉点位于两个1位之间(有两个可能的交叉点),则图式可能被破坏,它取决于x的值.但是如果交叉点在最右边的1位的右边(另外两个可能的交叉点),则图式不会被破坏;至少有一个子代会是h的实例.由此可见,图式被破坏的概率小于或等于1/2,它取决于交叉发生的位置.

一般化：
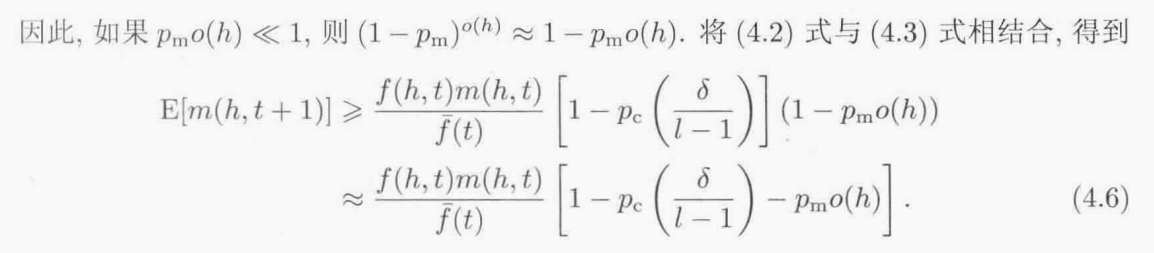
在这里插入图片描述

变异概率：
在这里插入图片描述
泰勒展开：
在这里插入图片描述
类比：
在这里插入图片描述

图式定理：
在这里插入图片描述
在这里插入图片描述

定理4.1 具有高于平均适应度值的短的低阶图式在遗传算法种群中的代表数会呈指数增长.

4.2 马尔可夫链

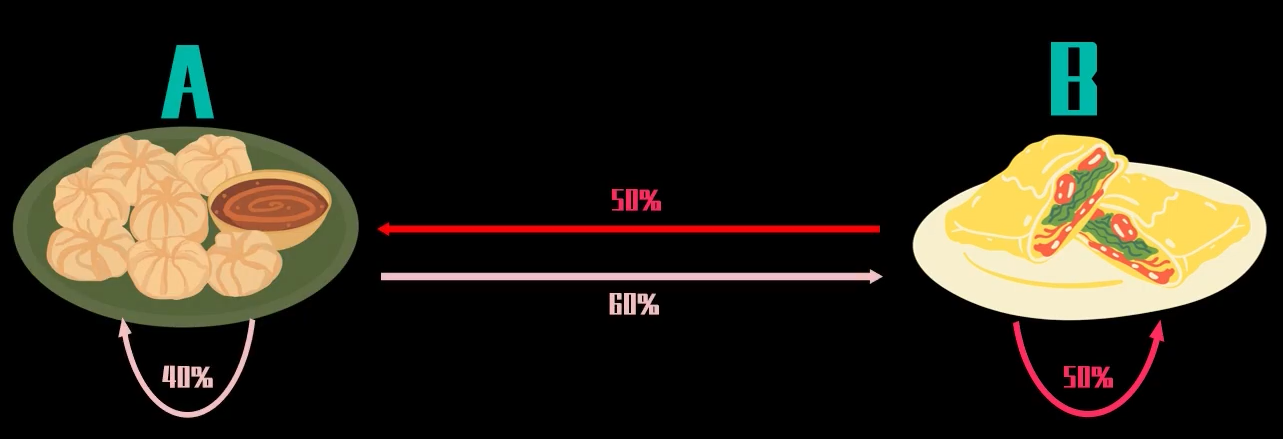
在这里插入图片描述
马尔可夫链的核心三要素：

  • 状态空间
  • 无记忆性
  • 转移矩阵

在这里插入图片描述

在这里插入图片描述

假设在时刻1状态：
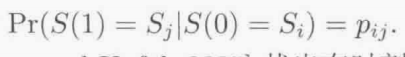
在这里插入图片描述

则在时刻2处于状态1的概率：
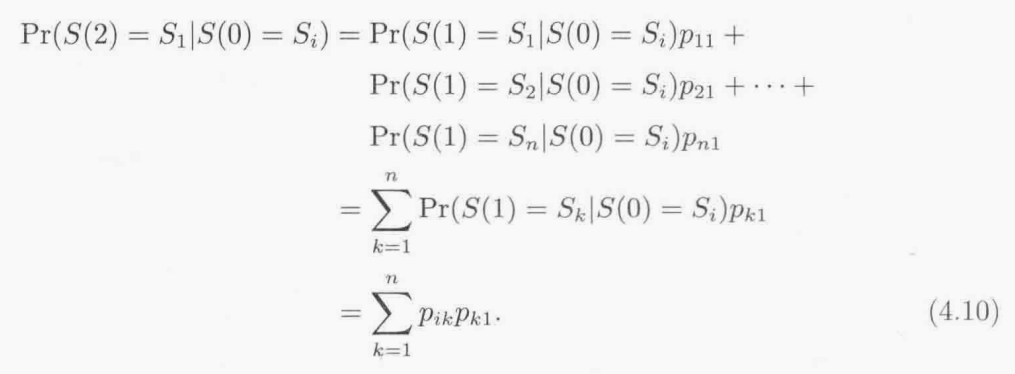
在这里插入图片描述
将上面的推导一般化,我们发现在时刻2过程处于状态j的概率为
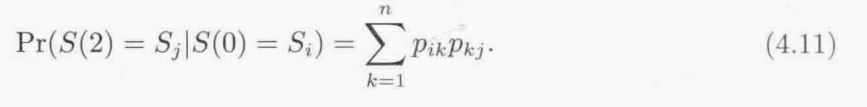
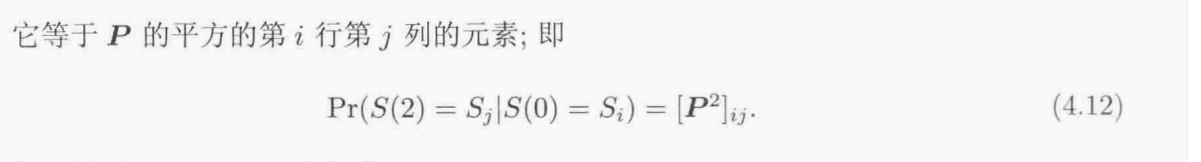
在这里插入图片描述
在这里插入图片描述

继续推理：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

假设不知马尔可夫的初始状态，但是知道每个状态的概率，初始状态S(0)等于Sk的概率为pk(0），利用全概率定理得：
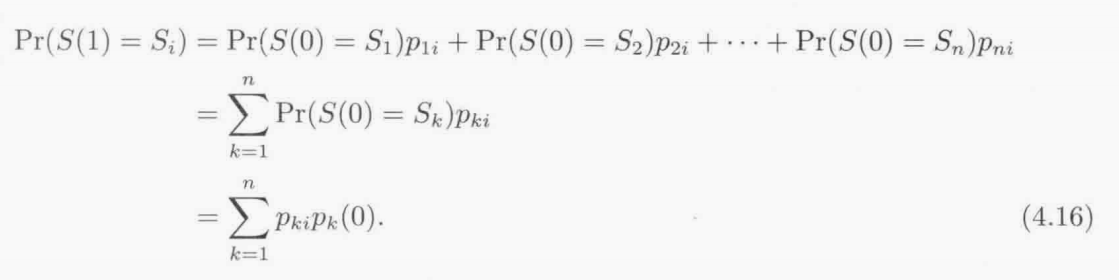
在这里插入图片描述
一般化：
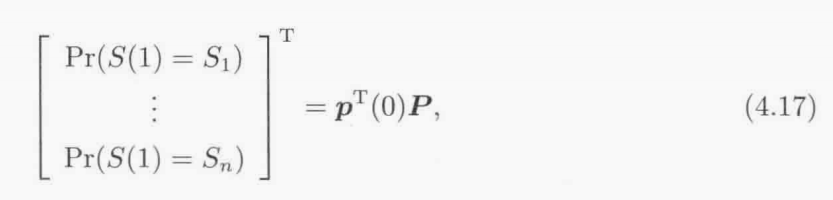
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.3 进化算法的马尔可夫模型的符号

4.4 遗传算法的马尔可夫模型

4.4.1 选择

4.4.2 变异

4.4.3 交叉

4.5 遗传算法的动态系统模型

4.5.1 选择

4.5.2 变异

4.5.3 交叉

相关文章：

《进化优化》第4章 遗传算法的数学模型

文章目录 4.1 图式理论4.2 马尔可夫链4.3 进化算法的马尔可夫模型的符号4.4 遗传算法的马尔可夫模型4.4.1 选择4.4.2 变异4.4.3 交叉 4.5 遗传算法的动态系统模型4.5.1 选择4.5.2 变异4.5.3 交叉 4.1 图式理论 图式是描述一组个体的位模式，其中用*来表示不在乎的位…...

编程日记 2023/10/14 0:34:37

spring：详解spring MVC

spring MVC SpringMVC是一种基于Java的MVC（Model-View-Controller）Web开发框架，通过将业务逻辑、数据和界面分离，使得开发人员能够更高效地管理和维护代码，提高应用的可扩展性和可维护性。 SpringMVC核心概念 Contr…...

编程日记 2023/10/14 0:33:36

【Leetcode】207.课程表

一、题目 1、题目描述 你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 p r e r e q u i s i t e s [ i ] = [ a i , b...

编程日记 2023/10/14 0:32:35

Ubuntu18.04中QT安装下载安装pcl和vtk以及使用过程中踩过的坑

一、先记录一下下载过程中踩过的坑 问题1：QVTKOpenGLNativeWidget和QVTKWidget 之前从来没有接触过QT中显示3D点云方面的知识，了解到可以用pcl，然后在网上各种找pcl下载的相关内容，想要在QT中显示出来，需要用到VTK&a…...

编程日记 2023/10/14 0:31:32

C++学习——对象数组、成员对象与封闭类

以下内容源于C语言中文网的学习与整理，非原创，如有侵权请告知删除。 一、对象数组 对象数组，即数组的每个元素都是某个类的对象。 1、对象数组中的每个元素都需要用构造函数初始化，具体哪些元素用哪些构造函数初始化&#xff0c…...

编程日记 2023/10/14 0:30:31

解锁机器学习-梯度下降：从技术到实战的全面指南

目录 一、简介什么是梯度下降？为什么梯度下降重要？ 二、梯度下降的数学原理代价函数（Cost Function）梯度（Gradient）更新规则代码示例：基础的梯度下降更新规则 三、批量梯度下降（Batc…...

编程日记 2023/10/14 0:29:31

day62:ARMday9,I2c总线通信

作业&#xff1a;按键中断实现LED1、蜂鸣器、风扇 key_in.c: #include "key_in.h"void gpio_init() {//RCC使能//GPIOERCC->MP_AHB4ENSETR | (0x1<<4);//GPIOBRCC->MP_AHB4ENSETR | (0x1<<1);//PE10、PB6、PE9输出模式GPIOE->MODER & ~(0…...

编程日记 2023/10/14 0:28:30

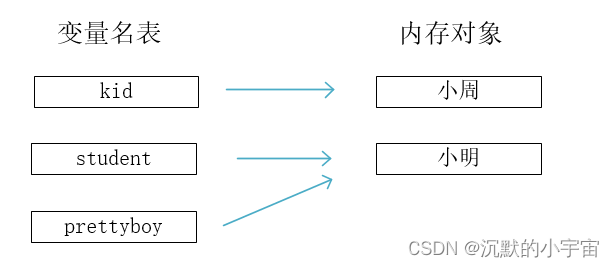
【Python学习笔记】类型/运算/变量/注释

前言 人生苦短&#xff0c;追求生产力&#xff0c;做一只时代风口的猪&#xff0c;应该学python Python语言中&#xff0c;所有的数据都被称之为对象。 1. 对象类型 Python语言中&#xff0c;常用的数据类型有&#xff1a; 整数&#xff0c; 比如 3 小数&#xff08;也叫浮…...

编程日记 2023/10/14 0:27:29

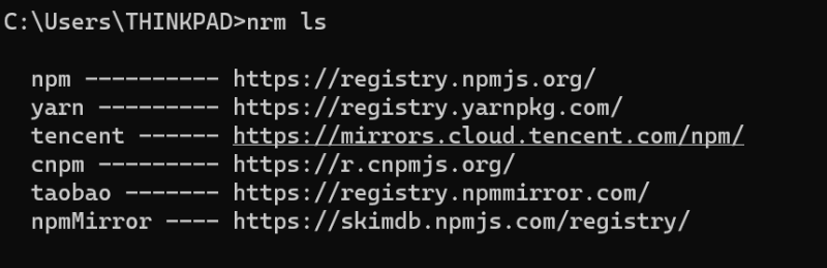
国内常用源开发环境换源(flutter换源，python换源，Linux换源，npm换源)

flutter换源 使用环境变量:PUB_HOSTED_URL FLUTTER_STORAGE_BASE_URL&#xff0c; upgrade出问题时可能会提示设置FLUTTER_GIT_URL变量。 flutter中国 PUB_HOSTED_URLhttps://pub.flutter-io.cn FLUTTER_STORAGE_BASE_URLhttps://storage.flutter-io.cn FLUTTER_GIT_URLhtt…...

编程日记 2023/10/14 0:26:27

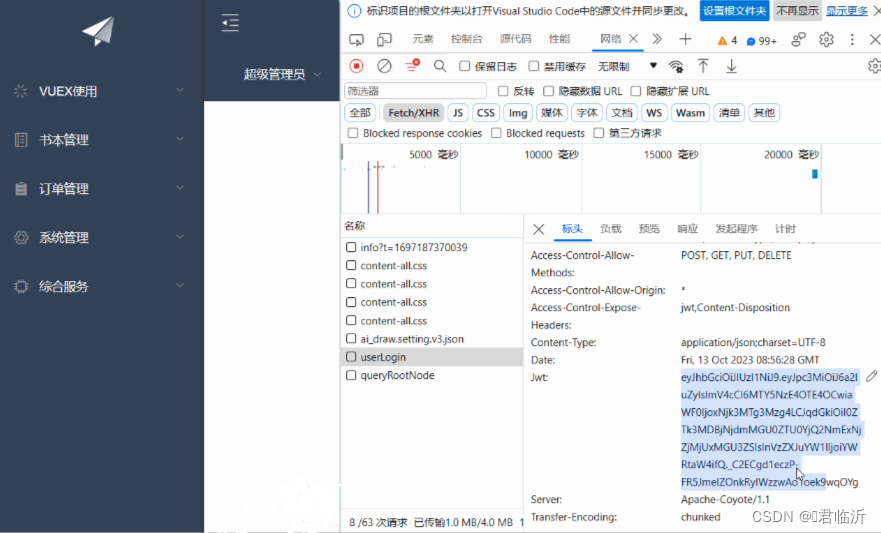
关于一篇什么是JWT的原理与实际应用

目录 一.介绍 1.1.什么是JWT 二.结构 三.Jwt的工具类的使用 3.1. 依赖 3.2.工具类 3.3.过滤器 3.4.控制器 3.5.配置 3.6. 测试类 用于生成JWT 解析Jwt 复制jwt&#xff0c;并延时30分钟 测试JWT的有效时间 测试过期JWT的解析 四.应用 今天就到这了&#xff0c;希…...

编程日记 2023/10/14 0:25:26

【Method】把 arXiv论文 转换为 HTML5 网页

文章目录 MethodReference https://ar5iv.labs.arxiv.org/ Articles from arXiv.org as responsive HTML5 web pages. 可以将来自 arXiv 的 PDF 论文渲染成 HTML5 网页版本。 Method View any arXiv article URL by changing the X to a 5. 将 arXiv 网址中的 x 换成 5 再回…...

编程日记 2023/10/14 0:24:25

每日一题AC

4.小花和小草正在沙滩上玩挖沙洞的游戏。他们划了一条长度为n米的线作为挖沙洞的参考线路&#xff0c;小花和小草分别从两头开始沿着划好的线开始挖洞&#xff0c;小花每隔a米挖一个洞&#xff0c;小草每隔b米挖一个洞&#xff0c;碰到已经挖过洞的就不需要再挖了。那么&#x…...

编程日记 2023/10/14 0:23:24

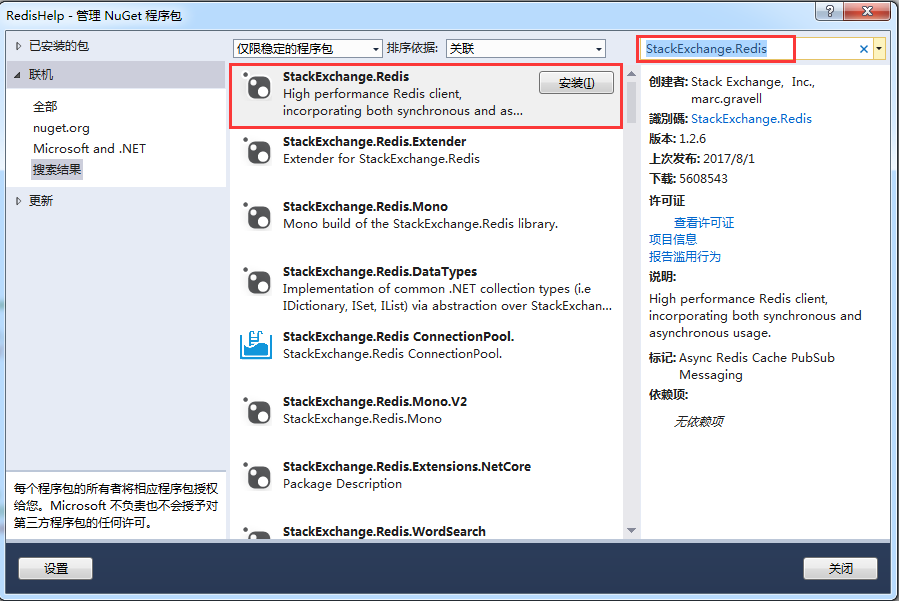
后端：推荐 2 个 .NET 操作的 Redis 客户端类库

目录 Redis特点 Redis场景 1. StackExchange.Redis 2. FreeRedis &#x1f680; 快速入门 &#x1f3a3; Master-Slave (读写分离) &#x1f4bb; Pipeline (管道)示例 &#x1f30c; Redis Cluster (集群) Redis &#xff0c;是一个高性能(NOSQL)的key-value数据库,Re…...

编程日记 2023/10/14 0:22:23

华泰证券：京东营收增长或短期承压

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 猛兽财经获悉&#xff0c;华泰证券近期发布研报称京东营收增长或短期承压。华泰证券主要观点如下&#xff1a;营收增长或短期承压&#xff0c;聚焦长期内生能力建设 考虑到消费情绪的恢复仍需一定时间&#xff0c;我们预计…...

编程日记 2023/10/14 0:21:21

Java从resources文件下载文档,文档没有后缀名

业务场景&#xff1a;因为公司会对excel文档加密&#xff0c;通过svn或者git上传代码也会对文档进行加密&#xff0c;所以这里将文档后缀去了&#xff0c;这样避免文档加密。 实现思路&#xff1a;将文档去掉后缀&#xff0c;放入resources下&#xff0c;获取输入流&#xff0…...

编程日记 2023/10/14 0:20:19

【动手学深度学习-Pytorch版】BERT预测系列——BERTModel

本小节主要实现了以下几部分内容&#xff1a; 从一个句子中提取BERT输入序列以及相对的segments段落索引&#xff08;因为BERT支持输入两个句子&#xff09;BERT使用的是Transformer的Encoder部分&#xff0c;所以需要需要使用Encoder进行前向传播&#xff1a;输出的特征等于词…...

编程日记 2023/10/14 0:19:19

Python之元组、字典和集合练习

1、餐厅下午茶 &#xff08;列表与元组 crr66&#xff09; 某餐厅推出了优惠下午茶套餐活动。顾客可以以优惠的价格从给定的糕点和给定的饮 料中各选一款组成套餐。已知&#xff0c;指定的糕点包括松饼(Muffins)、提拉米苏(Tiramisu)、芝士蛋 糕(Cheese Cake)和三明治(Sandwic…...

编程日记 2023/10/14 0:18:18

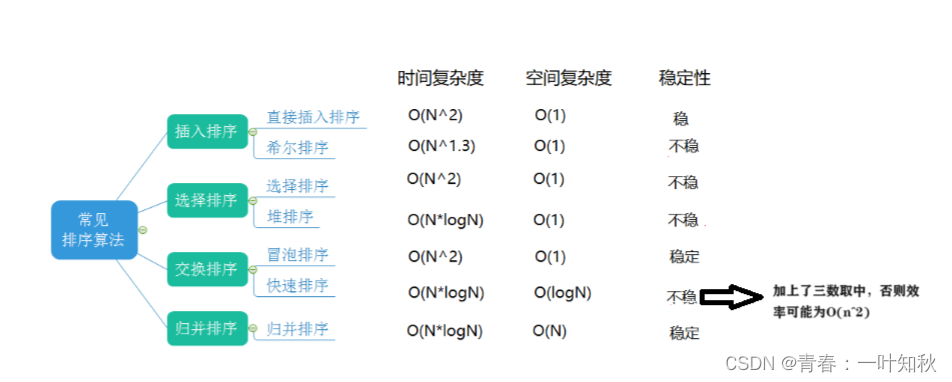
【数据结构】归并排序和计数排序(排序的总结)

目录 一&#xff0c;归并排序的递归 二&#xff0c;归并排序的非递归 三&#xff0c;计数排序 四&#xff0c;排序算法的综合分析 一&#xff0c;归并排序的递归 基本思想&#xff1a; 归并采用的是分治思想&#xff0c;是分治法的一个经典的运用。该算法先将原数据进行拆…...

编程日记 2023/10/14 0:17:16

某医疗机构：建立S-SDLC安全开发流程，保障医疗前沿科技应用高质量发展

某医疗机构是头部资本集团旗下专注大健康领域战略性投资与运营的实业公司&#xff0c;市场规模超300亿。该医疗机构已完成数字赋能&#xff0c;形成了标准化、专业化、数字化的疾病和健康管理体系&#xff0c;将进一步规划战略方向&#xff0c;为人工智能纳米技术、高温超导、生…...

编程日记 2023/10/14 0:16:16

验证二叉搜索树的后序遍历序列

LCR 152. 验证二叉搜索树的后序遍历序列 class VerifyTreeOrder:"""LCR 152. 验证二叉搜索树的后序遍历序列https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/description/"""def solution(self, postorder: Lis…...

编程日记 2023/10/14 0:15:14

第三章 内存管理 一、内存的基础知识

目录 一、什么是内存 二、有何作用 三、常用数量单位 四、指令的工作原理 五、装入方式 1、绝对装入 2、可重定位装入&#xff08;静态重定位&#xff09; 3、动态运行时装入&#xff08;动态重定位&#xff09; 六、从写程序到程序运行 七、链接的三种方式 1、静态…...

编程日记 2023/10/14 0:14:13

【Java学习之道】Java常用集合框架

引言 在Java中&#xff0c;集合框架是一个非常重要的概念。它提供了一种方式&#xff0c;让你可以方便地存储和操作数据。Java中的集合框架包括各种集合类和接口&#xff0c;这些类和接口提供了不同的功能和特性。通过学习和掌握Java的集合框架&#xff0c;你可以更好地管理和…...

编程日记 2023/10/14 0:13:12

logicFlow 流程图编辑工具使用及开源地址

一、工具介绍 LogicFlow 是一款流程图编辑框架&#xff0c;提供了一系列流程图交互、编辑所必需的功能和灵活的节点自定义、插件等拓展机制。LogicFlow 支持前端研发自定义开发各种逻辑编排场景&#xff0c;如流程图、ER 图、BPMN 流程等。在工作审批配置、机器人逻辑编排、无…...

编程日记 2023/10/14 0:12:11

ATF(TF-A)/OPTEE之动态代码分析汇总

安全之安全(security)博客目录导读 1、ASAN(AddressSanitizer)地址消毒动态代码分析 2、ATF(TF-A)之UBSAN动态代码分析 3、OPTEE之KASAN地址消毒动态代码分析...

编程日记 2023/10/14 0:11:10

10-11 周三 shell xargs tr curl 做大事情

最近发现&#xff0c;shell的小工具非常的强大&#xff0c;简单记录下 tr命令 -d 删除字符串1中所有输入字符。-s 删除所有重复出现字符序列&#xff0c;只保留第一个&#xff1b;即将重复出现字符串压缩为一个字符串 -d 用于删除查询到的字符串中的空格。 [test3NH-DC-NM1…...

编程日记 2023/10/14 0:10:09

1.1 向量与线性组合

一、向量的基础知识 两个独立的数字 v 1 v_1 v1​ 和 v 2 v_2 v2​&#xff0c;将它们配对可以产生一个二维向量 v \boldsymbol{v} v&#xff1a; 列向量 v v [ v 1 v 2 ] v 1 v 的第一个分量 v 2 v 的第二个分量 \textbf{列向量}\,\boldsymbol v\kern 10pt\boldsymbol …...

编程日记 2023/10/14 0:08:07

django: You may need to add ‘localhost‘ to ALLOWED_HOSTS

参考:https://blog.csdn.net/qq_21744873/article/details/87857279 python manage.py runserver后页面访问失败&#xff0c;提示&#xff1a; DisallowedHost at /admin/ Invalid HTTP_HOST header: ‘localhost:8000’. You may need to add ‘localhost’ to ALLOWED_HOSTS…...

编程日记 2023/10/14 0:07:06

网络安全（黑客技术）—自学手册

1.网络安全是什么 网络安全可以基于攻击和防御视角来分类&#xff0c;我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术&#xff0c;而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高&#xff1b; 二、则是发展相对成熟…...

编程日记 2023/10/14 0:06:05

【Vue】之Vuex的入门使用，取值，修改值，同异步请求处理---保姆级别教学

一&#xff0c;Vuex入门 1.1 什么是Vuex Vuex是一个专门为Vue.js应用程序开发的状态管理库。它用于管理应用程序中的共享状态&#xff0c;它采用集中式存储管理应用的所有组件的状态&#xff0c;使得状态的管理变得简单和可预测 官方解释&#xff1a;Vuex 是一个专为 Vue.js 应…...

编程日记 2023/10/14 0:05:04

ubuntu20.04 nerf Instant-ngp (下) 复现，自建数据集，导出mesh

参考链接 Ubuntu20.04复现instant-ngp&#xff0c;自建数据集&#xff0c;导出mesh_XINYU W的博客-CSDN博客 GitHub - NVlabs/instant-ngp: Instant neural graphics primitives: lightning fast NeRF and more youtube上的一个博主自建数据集 https://www.youtube.com/watch…...

编程日记 2023/10/14 0:04:02