解锁机器学习-梯度下降:从技术到实战的全面指南
目录
- 一、简介
- 什么是梯度下降?
- 为什么梯度下降重要?
- 二、梯度下降的数学原理
- 代价函数(Cost Function)
- 梯度(Gradient)
- 更新规则
- 代码示例:基础的梯度下降更新规则
- 三、批量梯度下降(Batch Gradient Descent)
- 基础算法
- 代码示例
- 四、随机梯度下降(Stochastic Gradient Descent)
- 基础算法
- 代码示例
- 优缺点
- 五、小批量梯度下降(Mini-batch Gradient Descent)
- 基础算法
- 代码示例
- 优缺点
本文全面深入地探讨了梯度下降及其变体——批量梯度下降、随机梯度下降和小批量梯度下降的原理和应用。通过数学表达式和基于PyTorch的代码示例,本文旨在为读者提供一种直观且实用的视角,以理解这些优化算法的工作原理和应用场景。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。
一、简介
梯度下降(Gradient Descent)是一种在机器学习和深度学习中广泛应用的优化算法。该算法的核心思想非常直观:找到一个函数的局部最小值(或最大值)通过不断地沿着该函数的梯度(gradient)方向更新参数。
什么是梯度下降?
简单地说,梯度下降是一个用于找到函数最小值的迭代算法。在机器学习中,这个“函数”通常是损失函数(Loss Function),该函数衡量模型预测与实际标签之间的误差。通过最小化这个损失函数,模型可以“学习”到从输入数据到输出标签之间的映射关系。
为什么梯度下降重要?
-
广泛应用:从简单的线性回归到复杂的深度神经网络,梯度下降都发挥着至关重要的作用。
-
解决不可解析问题:对于很多复杂的问题,我们往往无法找到解析解(analytical solution),而梯度下降提供了一种有效的数值方法。
-
扩展性:梯度下降算法可以很好地适应大规模数据集和高维参数空间。
-
灵活性与多样性:梯度下降有多种变体,如批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-batch Gradient Descent),各自有其优点和适用场景。
二、梯度下降的数学原理
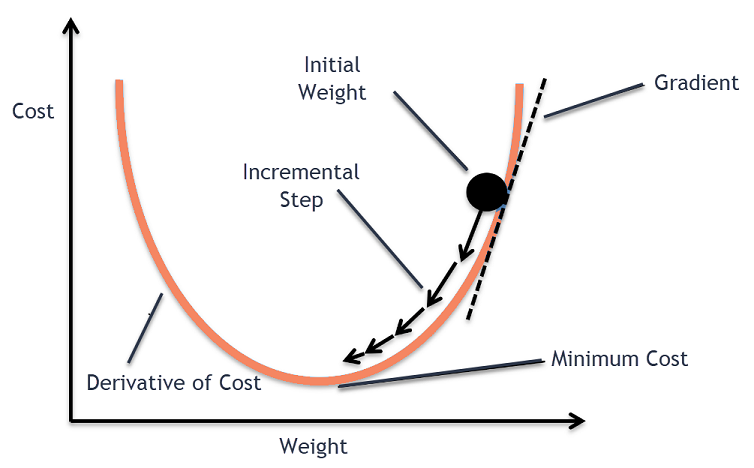
在深入研究梯度下降的各种实现之前,了解其数学背景是非常有用的。这有助于更全面地理解算法的工作原理和如何选择合适的算法变体。
代价函数(Cost Function)
在机器学习中,代价函数(也称为损失函数,Loss Function)是一个用于衡量模型预测与实际标签(或目标)之间差异的函数。通常用 ( J(\theta) ) 来表示,其中 ( \theta ) 是模型的参数。

梯度(Gradient)

更新规则

代码示例:基础的梯度下降更新规则
import numpy as npdef gradient_descent_update(theta, grad, alpha):"""Perform a single gradient descent update.Parameters:theta (ndarray): Current parameter values.grad (ndarray): Gradient of the cost function at current parameters.alpha (float): Learning rate.Returns:ndarray: Updated parameter values."""return theta - alpha * grad# Initialize parameters
theta = np.array([1.0, 2.0])
# Hypothetical gradient (for demonstration)
grad = np.array([0.5, 1.0])
# Learning rate
alpha = 0.01# Perform a single update
theta_new = gradient_descent_update(theta, grad, alpha)
print("Updated theta:", theta_new)
输出:
Updated theta: [0.995 1.99 ]
在接下来的部分,我们将探讨梯度下降的几种不同变体,包括批量梯度下降、随机梯度下降和小批量梯度下降,以及一些高级的优化技巧。通过这些内容,你将能更全面地理解梯度下降的应用和局限性。
三、批量梯度下降(Batch Gradient Descent)
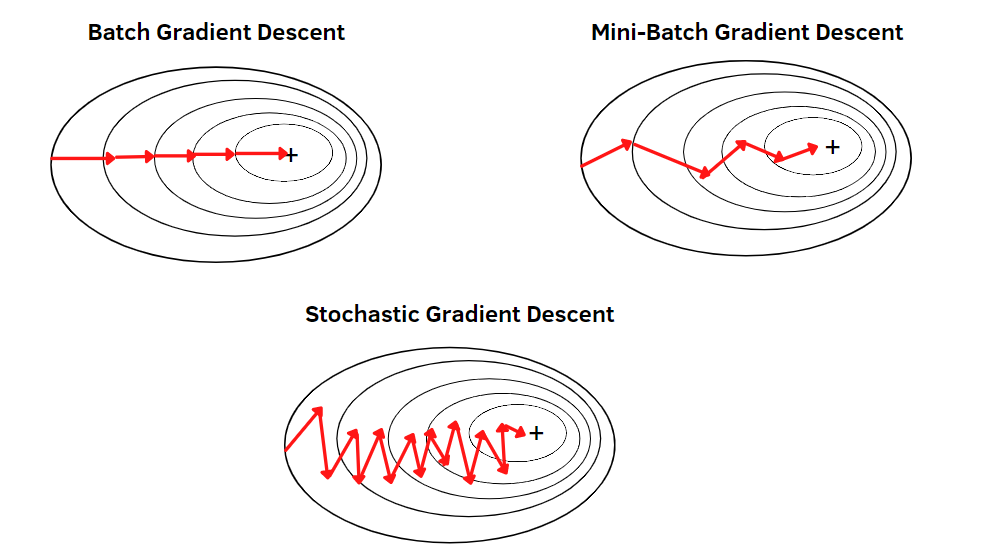
批量梯度下降(Batch Gradient Descent)是梯度下降算法的一种基础形式。在这种方法中,我们使用整个数据集来计算梯度,并更新模型参数。
基础算法
批量梯度下降的基础算法可以概括为以下几个步骤:

代码示例
下面的Python代码使用PyTorch库演示了批量梯度下降的基础实现。
import torch# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0]])# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)# Learning rate
alpha = 0.01# Number of iterations
n_iter = 1000# Cost function: Mean Squared Error
def cost_function(X, y, theta):m = len(y)predictions = X @ thetareturn (1 / (2 * m)) * torch.sum((predictions - y) ** 2)# Gradient Descent
for i in range(n_iter):J = cost_function(X, y, theta)J.backward()with torch.no_grad():theta -= alpha * theta.gradtheta.grad.zero_()print("Optimized theta:", theta)
输出:
Optimized theta: tensor([[0.5780],[0.7721]], requires_grad=True)
批量梯度下降的主要优点是它的稳定性和准确性,但缺点是当数据集非常大时,计算整体梯度可能非常耗时。接下来的章节中,我们将探索一些用于解决这一问题的变体和优化方法。
四、随机梯度下降(Stochastic Gradient Descent)
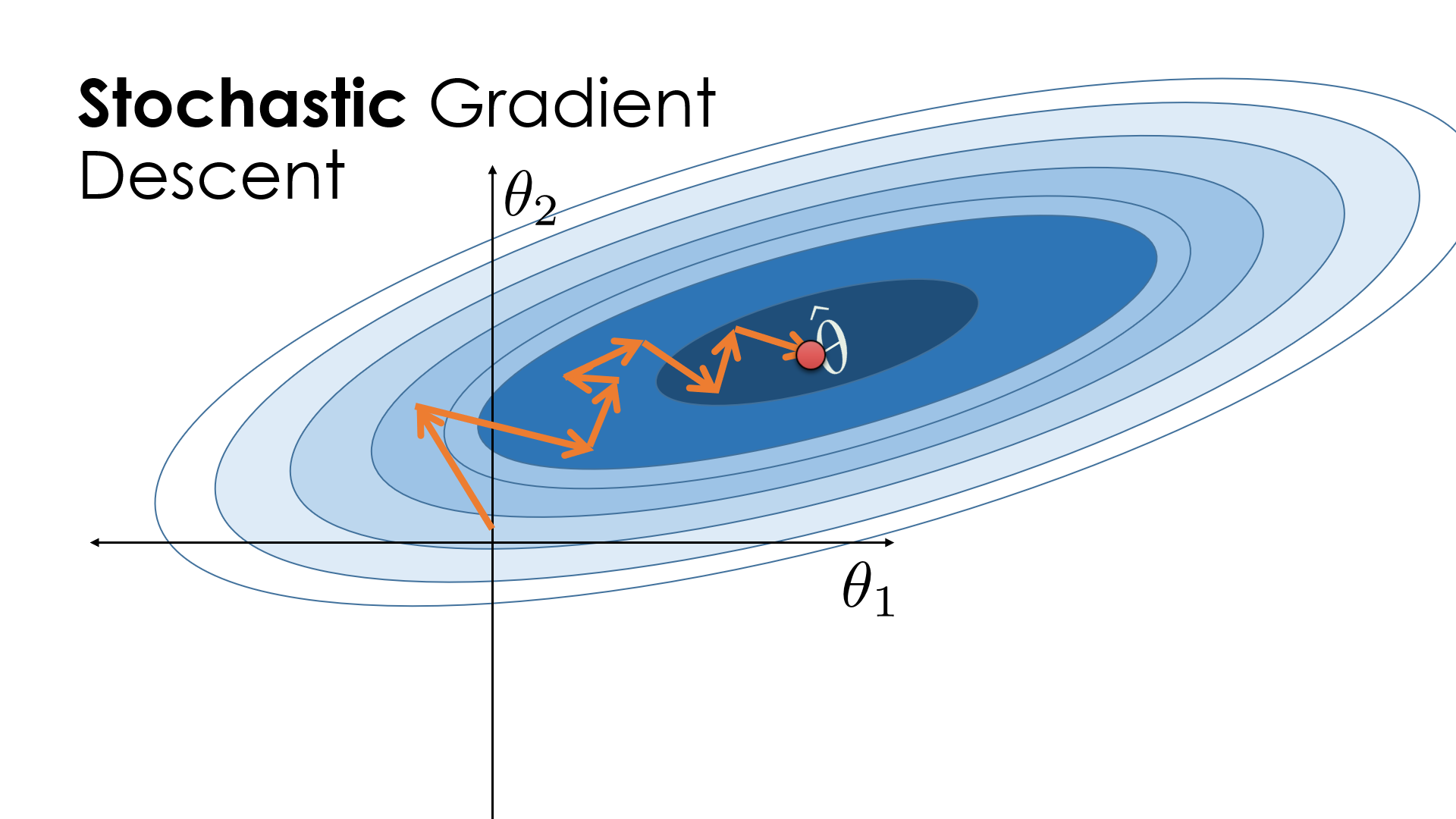
随机梯度下降(Stochastic Gradient Descent,简称SGD)是梯度下降的一种变体,主要用于解决批量梯度下降在大数据集上的计算瓶颈问题。与批量梯度下降使用整个数据集计算梯度不同,SGD每次只使用一个随机选择的样本来进行梯度计算和参数更新。
基础算法
随机梯度下降的基本步骤如下:

代码示例
下面的Python代码使用PyTorch库演示了SGD的基础实现。
import torch
import random# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0]])# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)# Learning rate
alpha = 0.01# Number of iterations
n_iter = 1000# Stochastic Gradient Descent
for i in range(n_iter):# Randomly sample a data pointidx = random.randint(0, len(y) - 1)x_i = X[idx]y_i = y[idx]# Compute cost for the sampled pointJ = (1 / 2) * torch.sum((x_i @ theta - y_i) ** 2)# Compute gradientJ.backward()# Update parameterswith torch.no_grad():theta -= alpha * theta.grad# Reset gradientstheta.grad.zero_()print("Optimized theta:", theta)
输出:
Optimized theta: tensor([[0.5931],[0.7819]], requires_grad=True)
优缺点
SGD虽然解决了批量梯度下降在大数据集上的计算问题,但因为每次只使用一个样本来更新模型,所以其路径通常比较“嘈杂”或“不稳定”。这既是优点也是缺点:不稳定性可能帮助算法跳出局部最优解,但也可能使得收敛速度减慢。
在接下来的部分,我们将介绍一种折衷方案——小批量梯度下降,它试图结合批量梯度下降和随机梯度下降的优点。
五、小批量梯度下降(Mini-batch Gradient Descent)
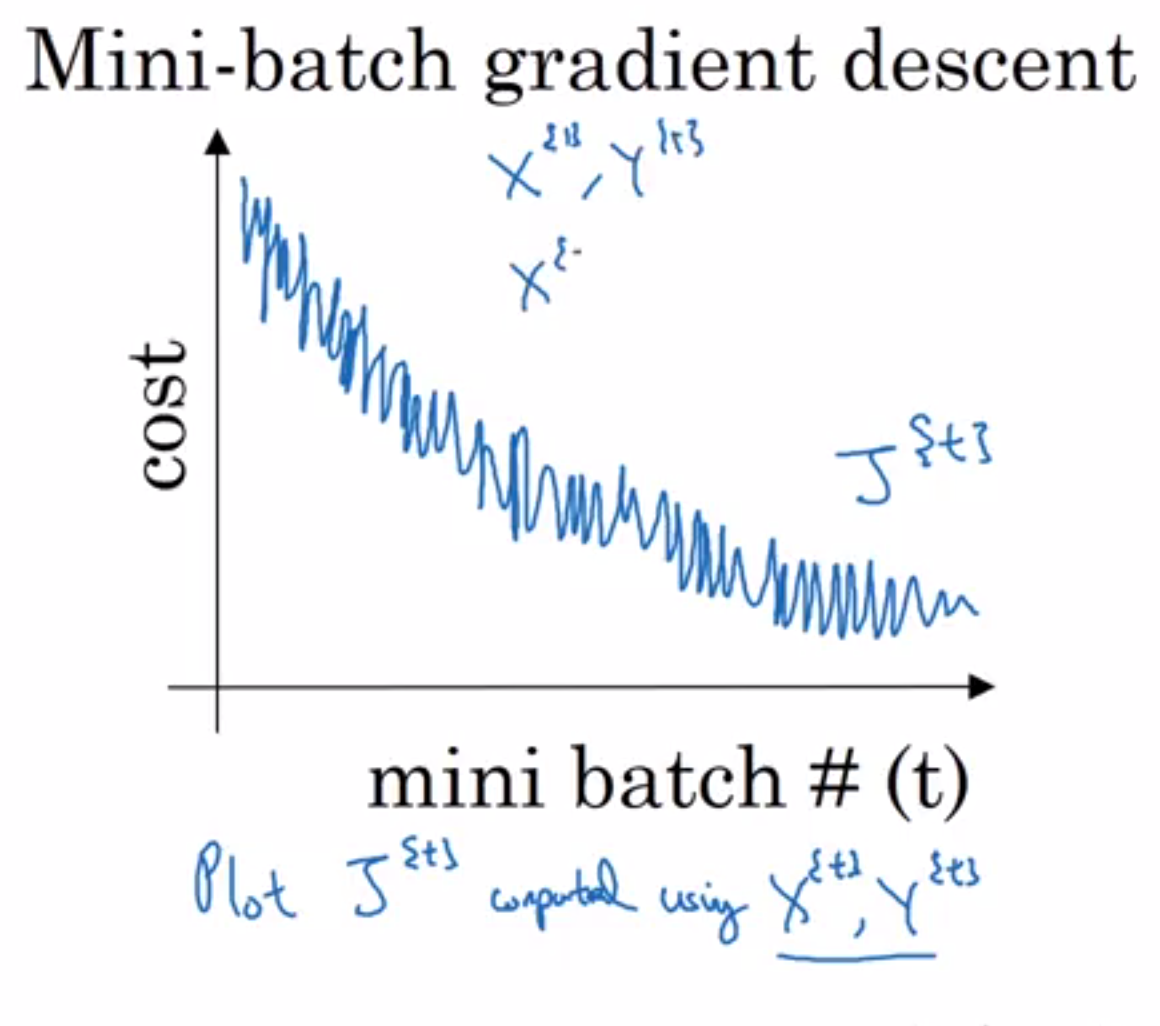
小批量梯度下降(Mini-batch Gradient Descent)是批量梯度下降和随机梯度下降(SGD)之间的一种折衷方法。在这种方法中,我们不是使用整个数据集,也不是使用单个样本,而是使用一个小批量(mini-batch)的样本来进行梯度的计算和参数更新。
基础算法
小批量梯度下降的基本算法步骤如下:

代码示例
下面的Python代码使用PyTorch库演示了小批量梯度下降的基础实现。
import torch
from torch.utils.data import DataLoader, TensorDataset# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0], [4.0, 5.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0], [4.0]])# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)# Learning rate and batch size
alpha = 0.01
batch_size = 2# Prepare DataLoader
dataset = TensorDataset(X, y)
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)# Mini-batch Gradient Descent
for epoch in range(100):for X_batch, y_batch in data_loader:J = (1 / (2 * batch_size)) * torch.sum((X_batch @ theta - y_batch) ** 2)J.backward()with torch.no_grad():theta -= alpha * theta.gradtheta.grad.zero_()print("Optimized theta:", theta)
输出:
Optimized theta: tensor([[0.6101],[0.7929]], requires_grad=True)
优缺点
小批量梯度下降结合了批量梯度下降和SGD的优点:它比SGD更稳定,同时比批量梯度下降更快。这种方法广泛应用于深度学习和其他机器学习算法中。
小批量梯度下降不是没有缺点的。选择合适的批量大小可能是一个挑战,而且有时需要通过实验来确定。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。
相关文章:

解锁机器学习-梯度下降:从技术到实战的全面指南
目录 一、简介什么是梯度下降?为什么梯度下降重要? 二、梯度下降的数学原理代价函数(Cost Function)梯度(Gradient)更新规则代码示例:基础的梯度下降更新规则 三、批量梯度下降(Batc…...

day62:ARMday9,I2c总线通信
作业:按键中断实现LED1、蜂鸣器、风扇 key_in.c: #include "key_in.h"void gpio_init() {//RCC使能//GPIOERCC->MP_AHB4ENSETR | (0x1<<4);//GPIOBRCC->MP_AHB4ENSETR | (0x1<<1);//PE10、PB6、PE9输出模式GPIOE->MODER & ~(0…...
【Python学习笔记】类型/运算/变量/注释
前言 人生苦短,追求生产力,做一只时代风口的猪,应该学python Python语言中,所有的数据都被称之为对象。 1. 对象类型 Python语言中,常用的数据类型有: 整数, 比如 3 小数(也叫浮…...
国内常用源开发环境换源(flutter换源,python换源,Linux换源,npm换源)
flutter换源 使用环境变量:PUB_HOSTED_URL FLUTTER_STORAGE_BASE_URL, upgrade出问题时可能会提示设置FLUTTER_GIT_URL变量。 flutter中国 PUB_HOSTED_URLhttps://pub.flutter-io.cn FLUTTER_STORAGE_BASE_URLhttps://storage.flutter-io.cn FLUTTER_GIT_URLhtt…...
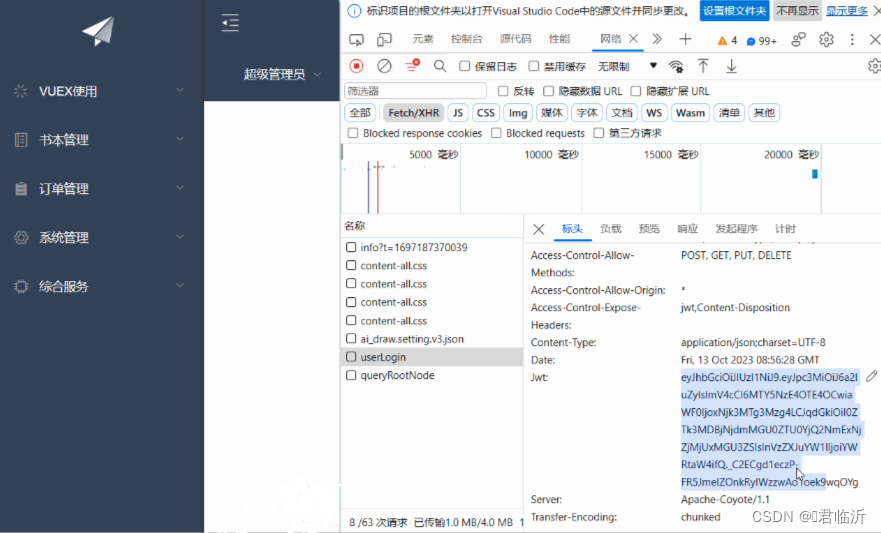
关于一篇什么是JWT的原理与实际应用
目录 一.介绍 1.1.什么是JWT 二.结构 三.Jwt的工具类的使用 3.1. 依赖 3.2.工具类 3.3.过滤器 3.4.控制器 3.5.配置 3.6. 测试类 用于生成JWT 解析Jwt 复制jwt,并延时30分钟 测试JWT的有效时间 测试过期JWT的解析 四.应用 今天就到这了,希…...

【Method】把 arXiv论文 转换为 HTML5 网页
文章目录 MethodReference https://ar5iv.labs.arxiv.org/ Articles from arXiv.org as responsive HTML5 web pages. 可以将来自 arXiv 的 PDF 论文渲染成 HTML5 网页版本。 Method View any arXiv article URL by changing the X to a 5. 将 arXiv 网址中的 x 换成 5 再回…...

每日一题AC
4.小花和小草正在沙滩上玩挖沙洞的游戏。他们划了一条长度为n米的线作为挖沙洞的参考线路,小花和小草分别从两头开始沿着划好的线开始挖洞,小花每隔a米挖一个洞,小草每隔b米挖一个洞,碰到已经挖过洞的就不需要再挖了。那么&#x…...
后端:推荐 2 个 .NET 操作的 Redis 客户端类库
目录 Redis特点 Redis场景 1. StackExchange.Redis 2. FreeRedis 🚀 快速入门 🎣 Master-Slave (读写分离) 💻 Pipeline (管道)示例 🌌 Redis Cluster (集群) Redis ,是一个高性能(NOSQL)的key-value数据库,Re…...

华泰证券:京东营收增长或短期承压
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,华泰证券近期发布研报称京东营收增长或短期承压。华泰证券主要观点如下:营收增长或短期承压,聚焦长期内生能力建设 考虑到消费情绪的恢复仍需一定时间,我们预计…...
Java从resources文件下载文档,文档没有后缀名
业务场景:因为公司会对excel文档加密,通过svn或者git上传代码也会对文档进行加密,所以这里将文档后缀去了,这样避免文档加密。 实现思路:将文档去掉后缀,放入resources下,获取输入流࿰…...

【动手学深度学习-Pytorch版】BERT预测系列——BERTModel
本小节主要实现了以下几部分内容: 从一个句子中提取BERT输入序列以及相对的segments段落索引(因为BERT支持输入两个句子)BERT使用的是Transformer的Encoder部分,所以需要需要使用Encoder进行前向传播:输出的特征等于词…...

Python之元组、字典和集合练习
1、餐厅下午茶 (列表与元组 crr66) 某餐厅推出了优惠下午茶套餐活动。顾客可以以优惠的价格从给定的糕点和给定的饮 料中各选一款组成套餐。已知,指定的糕点包括松饼(Muffins)、提拉米苏(Tiramisu)、芝士蛋 糕(Cheese Cake)和三明治(Sandwic…...
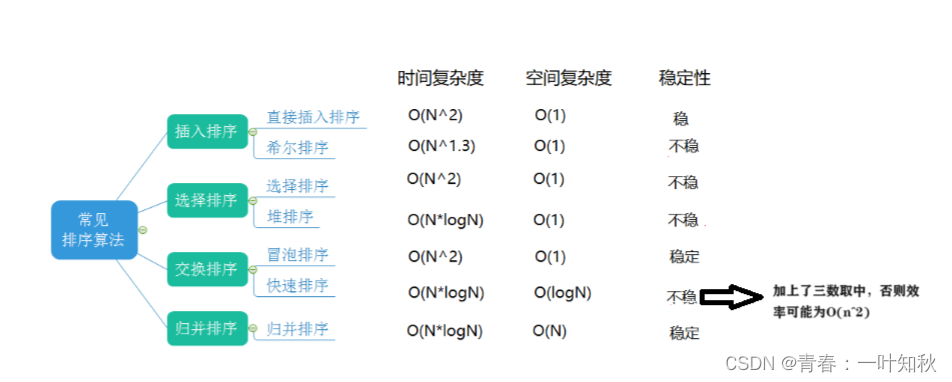
【数据结构】归并排序和计数排序(排序的总结)
目录 一,归并排序的递归 二,归并排序的非递归 三,计数排序 四,排序算法的综合分析 一,归并排序的递归 基本思想: 归并采用的是分治思想,是分治法的一个经典的运用。该算法先将原数据进行拆…...

某医疗机构:建立S-SDLC安全开发流程,保障医疗前沿科技应用高质量发展
某医疗机构是头部资本集团旗下专注大健康领域战略性投资与运营的实业公司,市场规模超300亿。该医疗机构已完成数字赋能,形成了标准化、专业化、数字化的疾病和健康管理体系,将进一步规划战略方向,为人工智能纳米技术、高温超导、生…...

验证二叉搜索树的后序遍历序列
LCR 152. 验证二叉搜索树的后序遍历序列 class VerifyTreeOrder:"""LCR 152. 验证二叉搜索树的后序遍历序列https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/description/"""def solution(self, postorder: Lis…...
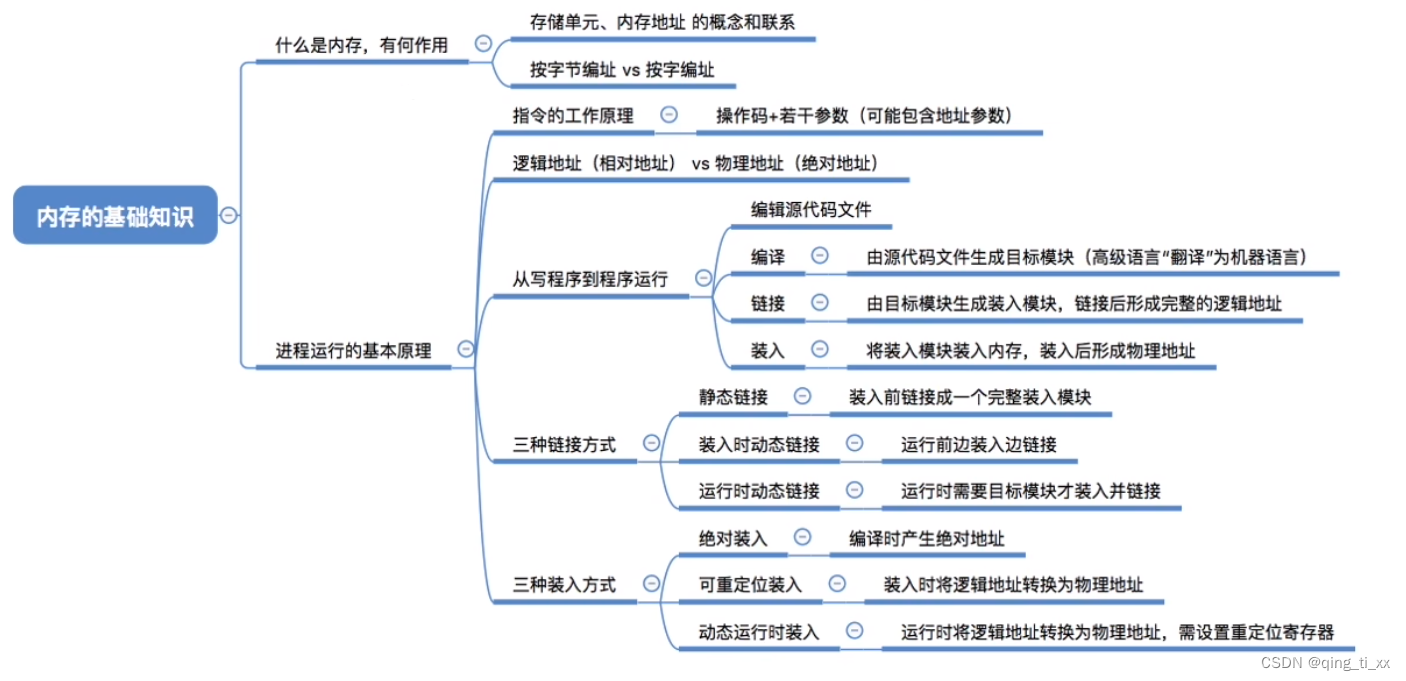
第三章 内存管理 一、内存的基础知识
目录 一、什么是内存 二、有何作用 三、常用数量单位 四、指令的工作原理 五、装入方式 1、绝对装入 2、可重定位装入(静态重定位) 3、动态运行时装入(动态重定位) 六、从写程序到程序运行 七、链接的三种方式 1、静态…...

【Java学习之道】Java常用集合框架
引言 在Java中,集合框架是一个非常重要的概念。它提供了一种方式,让你可以方便地存储和操作数据。Java中的集合框架包括各种集合类和接口,这些类和接口提供了不同的功能和特性。通过学习和掌握Java的集合框架,你可以更好地管理和…...
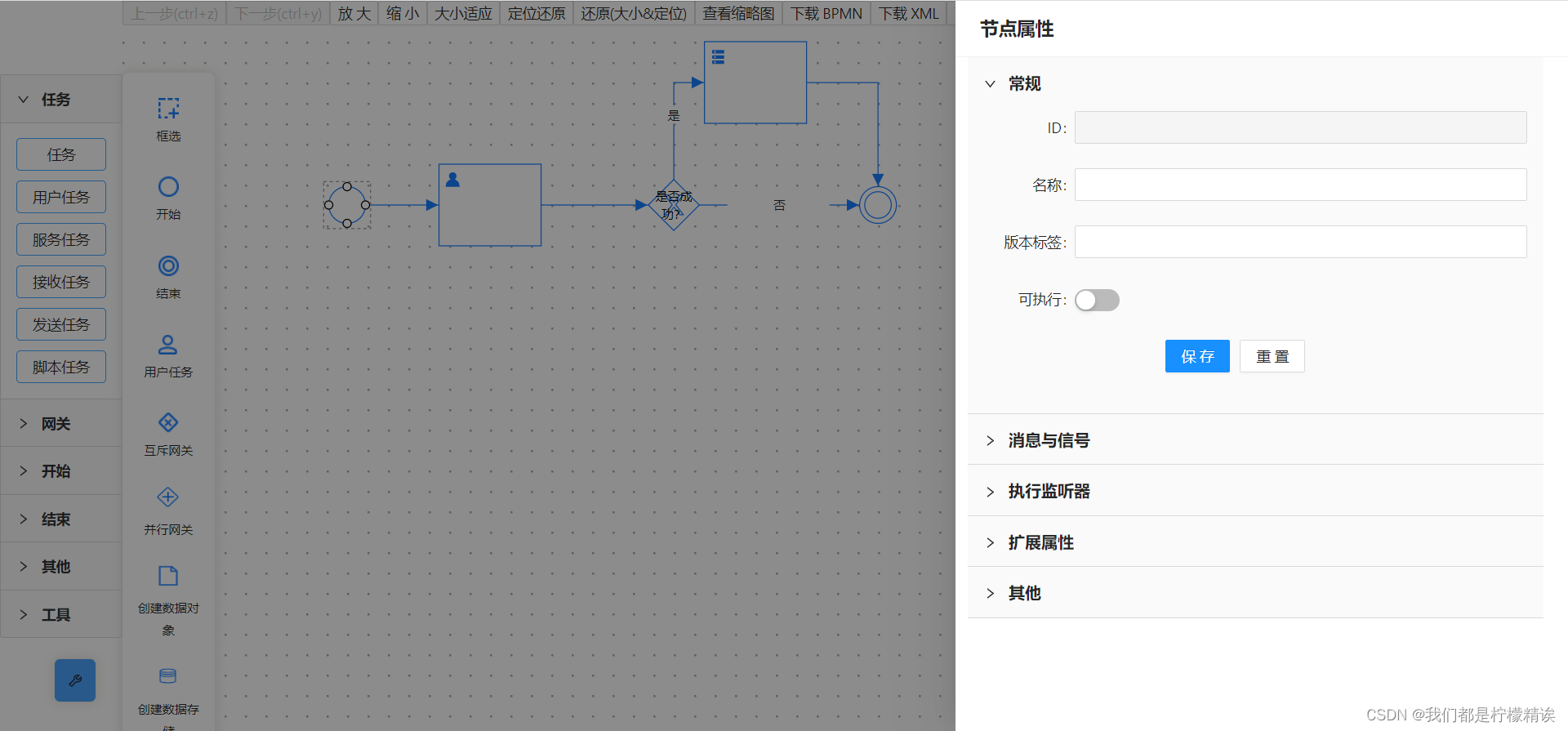
logicFlow 流程图编辑工具使用及开源地址
一、工具介绍 LogicFlow 是一款流程图编辑框架,提供了一系列流程图交互、编辑所必需的功能和灵活的节点自定义、插件等拓展机制。LogicFlow 支持前端研发自定义开发各种逻辑编排场景,如流程图、ER 图、BPMN 流程等。在工作审批配置、机器人逻辑编排、无…...
/OPTEE之动态代码分析汇总)
ATF(TF-A)/OPTEE之动态代码分析汇总
安全之安全(security)博客目录导读 1、ASAN(AddressSanitizer)地址消毒动态代码分析 2、ATF(TF-A)之UBSAN动态代码分析 3、OPTEE之KASAN地址消毒动态代码分析...

10-11 周三 shell xargs tr curl 做大事情
最近发现,shell的小工具非常的强大,简单记录下 tr命令 -d 删除字符串1中所有输入字符。-s 删除所有重复出现字符序列,只保留第一个;即将重复出现字符串压缩为一个字符串 -d 用于删除查询到的字符串中的空格。 [test3NH-DC-NM1…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
