动态规划 -背包问题-详解
问题
注:大佬对此类问题的解法:动态规划背包问题总结
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 1000
nums 中的所有元素 互不相同
1 <= target <= 1000
程序
#include <stdio.h>// 定义一个函数来计算总和为目标整数的元素组合的个数
int combinationSum4(int* nums, int numsSize, int target) {// 创建一个动态规划数组 dp,长度为 target + 1int dp[target + 1];// 初始化 dp 数组,将所有元素初始化为0for (int i = 0; i <= target; i++) {dp[i] = 0;}// 初始状态:总和为0时,只有一种组合方式,即什么都不选dp[0] = 1;// 开始填充 dp 数组for (int i = 1; i <= target; i++) {for (int j = 0; j < numsSize; j++) {// 如果当前的目标总和减去数组元素可达if (i - nums[j] >= 0) {// 则将 dp[i] 增加 dp[i - nums[j]],表示加上当前元素后的组合数dp[i] += dp[i - nums[j]];}}}// 返回 dp 数组中最终目标总和的组合数return dp[target];
}int main() {int nums[] = {1, 2, 3};int target = 4;int numsSize = sizeof(nums) / sizeof(nums[0]);// 调用 combinationSum4 函数,计算组合数int result = combinationSum4(nums, numsSize, target);// 打印结果printf("输出:%d\n", result);return 0;
}解释
在动态规划中,dp[i - nums[j]] 表示以目标值 i 减去数组中的某个元素 nums[j] 后的状态。这通常用于动态规划问题中,特别是在处理组合问题时,来记录前一步的状态。
在上述程序中,dp[i] 表示总和为 i 的组合数。当计算 dp[i] 时,我们遍历数组 nums 中的元素,对于每个元素 nums[j],我们考虑将其加入总和为 i 的组合中。为了计算 dp[i],我们需要考虑两种情况:
- 如果 i 大于等于 nums[j],那么我们可以将 nums[j] 加入到总和为 i 的组合中。此时,我们需要考虑的是将 nums[j] 加入后,剩余的总和为 i - nums[j] 的组合数,这就是 dp[i - nums[j]]。
- 如果 i 小于 nums[j],则 nums[j] 不能被加入到总和为 i 的组合中,因为它会导致总和超过
i。因此,在这种情况下,dp[i - nums[j]] 为0。
所以,dp[i - nums[j]] 表示以目标值 i 减去数组中的某个元素 nums[j] 后的状态,即剩余的部分。通过考虑所有可能的 nums[j],我们可以累加所有这些情况,以计算总和为 i 的组合数 dp[i]。这就是动态规划的思想:将较大问题分解成较小问题,并使用较小问题的解来构建较大问题的解。
假设数组 nums 为 [1, 2, 3],目标值 target 为 4。
初始时,dp 数组如下:
dp[0] = 1
dp[1] = 0
dp[2] = 0
dp[3] = 0
dp[4] = 0开始计算 dp[1]:
- i 等于 1,nums[j] 等于 1,因此 i >= nums[j]。
- 我们考虑将 1 加入到总和为 1 的组合中,剩余的总和是 1 - 1 = 0。
- 此时,dp[0] 为1,因为只有一种组合方式,即什么都不选。
- 所以,dp[1] = dp[1 - 1] = dp[0] = 1。
继续计算 dp[2] 和 dp[3]: - dp[2] 的计算和 dp[1] 类似,因为我们可以将 2 加入到总和为 2 的组合中,dp[2] = dp[2 - 2] = dp[0] = 1。
- dp[3] 的计算也类似,因为我们可以将 3 加入到总和为 3 的组合中,dp[3] = dp[3 - 3] = dp[0] = 1。
最后,计算 dp[4]: - 对于 dp[4],我们可以考虑将 1 加入到总和为 4 的组合中,这就是 dp[4 - 1] = dp[3] = 1。
- 我们还可以考虑将 2 加入到总和为 4 的组合中,这就是 dp[4 - 2] = dp[2] = 1。
- 同样,我们可以考虑将 3 加入到总和为 4 的组合中,这就是 dp[4 - 3] = dp[1] = 1。
- 然后,将这些情况的组合数累加起来,即 dp[4] = 1 + 1 + 1 = 3。
最终,dp[4] 的值为 3,表示总和为 4 的组合数为 3 种,即 [1, 1, 1, 1]、[1, 1, 2] 和 [2, 2]。
相关文章:

动态规划 -背包问题-详解
问题 注:大佬对此类问题的解法:动态规划背包问题总结 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围。 示例 1ÿ…...
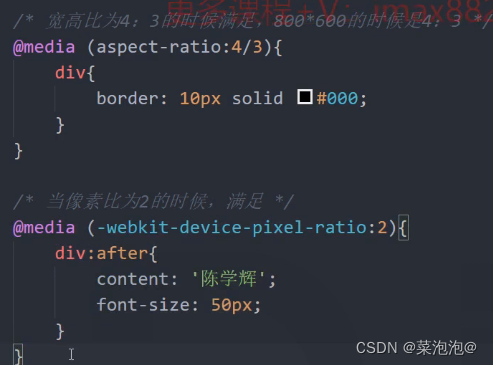
Bootstrap-- 媒体特性
最大、最小宽度例子: 横屏与竖屏例子: 宽度比与像素比例子:...

c# 用非递归的写法实现递归
最近写代码碰到了一个bug,就是递归次数太多爆堆栈了,然后就写了一个递归工具来解决这个问题。 using System; using System.Collections.Generic;/// <summary> /// 递归工具 /// </summary> public static class RecursionTool {//递归方式…...
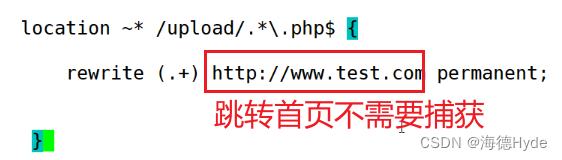
nginx之location的优先级和nginx的重定向
一、nginx之location的优先级和匹配方式(重点) (一)nginx的正则表达式 nginx的正则表达式 符号 含义 ^ 字符串的起始位置(以什么开头) $ 字符串的结束位置(以什么结尾) * 匹…...

【计算机网络】——前言计算机网络发展的历程概述
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法:算法专栏 C头…...

eventfd
1. #include <sys/eventfd.h> int eventfd(unsigned int initval, int flags); //创建eventfd 参数含义: initval:创建eventfd时它所对应的64位计数器的初始值; flags:eventfd文件描述符的标志,可由三种选项组…...

BES耳机空间音频技术实现
BES耳机空间音频技术实现 是否需要申请加入数字音频系统研究开发交流答疑群(课题组)?加我微信hezkz17, 本群提供音频技术答疑服务 音响和耳机在空间音频技术上实现方式是不同的 虚拟现实可谓是空间音频技术最具代表性的应 用领域。虽然虚拟现实的起源可以追溯到1 9 6 8年, …...
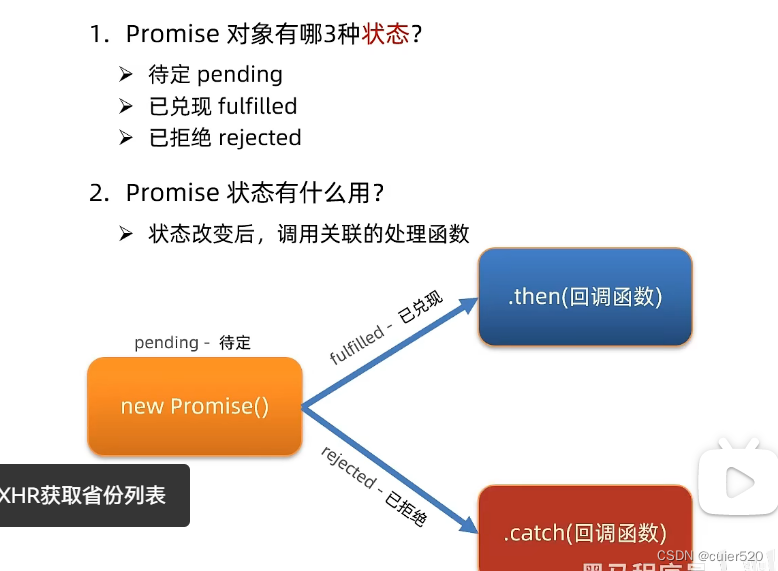
day27--AJAX(bootstrap之modal,toast;接口文档的一些用法;AJAX原理)
目录 Bootstrap之Modal: 显示和隐藏方法 通过自定义属性: 使用JS来控制弹框: Bootstrap之Toast: 接口文档一些用法: 删除图书: 图片上传: 图片上传步骤: 修改头像…...
:杂七杂八的记录)
【ArcGIS Pro二次开发】(70):杂七杂八的记录
本文用于记录一些使用频率较高但归类繁杂,非系统性的一些代码。 主要方便自己使用和查阅,随时更新。 1、从GDB数据库中打开【FeatureDataset\FeatureClass\Table】 using Geodatabase gdb new Geodatabase(new FileGeodatabaseConnectionPath(new Uri…...
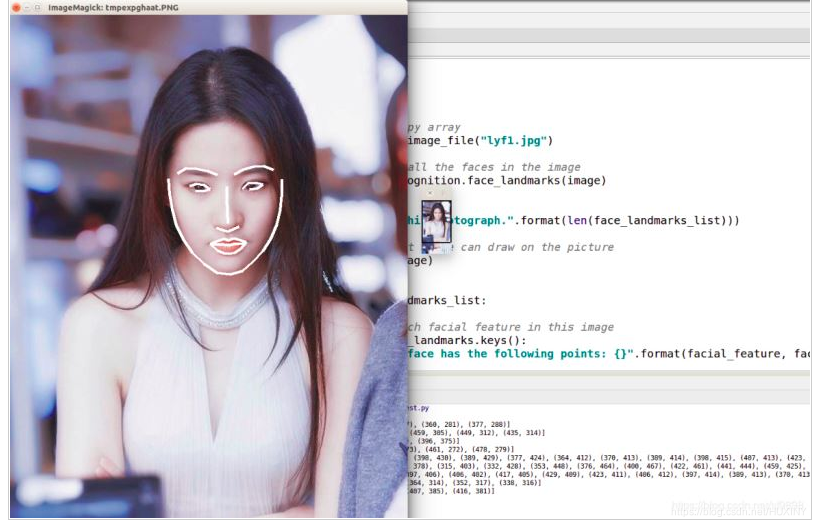
竞赛选题 深度学习 机器视觉 人脸识别系统 - opencv python
文章目录 0 前言1 机器学习-人脸识别过程人脸检测人脸对其人脸特征向量化人脸识别 2 深度学习-人脸识别过程人脸检测人脸识别Metric Larning 3 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习 机器视觉 人脸识别系统 该项目…...
【工具】SSH端口转发管理器,专门管理SSH Port Forwarding
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 开源代码看这里:http://xfxuezhang.cn/index.php/archives/1151/ 背景介绍 有时候需要用到ssh的端口转发功能。目前来说,要么是cmd里手敲指令,但每次敲也太麻烦了;或…...

opencv-phase 函数
计算梯度强度和方向 梯度的方向与边缘的方向总是垂直的。图像中的边缘可以指向各个方向,通常会取水平(左、右)、垂直(上、下)、对角线(左上、右上、左下、右下)等八个不同的方向计算梯度。 角度…...
44.ES
一、ES。 (1)es概念。 (1.1)什么是es。 (1.2)es的发展。 es是基于lucene写的。 (1.3)总结。 es是基于lucene写的。 (2)倒排索引。 (3…...

分权分域有啥内容?
目前的系统有什么问题? 现在我们的系统越来越庞大,可是每一个人进来的查看到的内容完全一样,没有办法灵活的根据不同用户展示不同的数据 例如我们有一个系统,期望不同权限的用户可以看到不同类型的页面,同一个页面不…...
6.Docker搭建RabbitMQ
1、端口开放 如果在云服务上部署需在安全组开通一下端口:15672、5672、25672、61613、1883。 15672(UI页面通信口)、5672(client端通信口)、25672(server间内部通信口)、61613(stomp 消息传输)、1883(MQTT消息队列遥测传输)。 2、安装镜像 docker pull rabbitmq 3、…...
用 docker 创建 jmeter 容器, 实现性能测试,该如何下手?
用 docker 创建 jmeter 容器, 实现性能测试 我们都知道,jmeter可以做接口测试,也可以用于性能测试,现在企业中性能测试也大多使用jmeter。docker是最近这些年流行起来的容器部署工具,可以创建一个容器,然后把项目放到…...

4年软件测试,突破不了20K,太卷了。。。
先说一个插曲:上个月我有同学在深圳被裁员了,和我一样都是软件测试,不过他是平安外包,所以整个组都撤了,他工资和我差不多都是14K。 现在IT互联网已经比较寒冬,特别是软件测试,裁员先裁测试&am…...
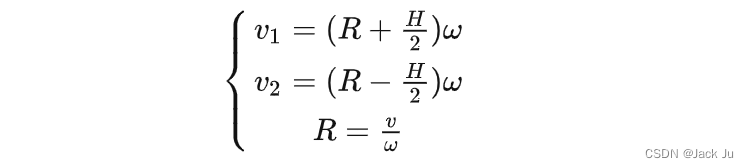
机器人控制算法——两轮差速驱动运动模型
1.Introduction 本文主要介绍针对于两轮差速模型的逆运动学数学推导。因为在机器人控制领域,决策规划控制层给执行器输出的控制指令v(车辆前进速度)和w(角速度),因此,我们比较关心,当底层两个驱动电机接收到此信息,如何…...

Queue简介
概念: 队列(Queue)是一种常见的线性数据结构,在Java中用于存储和操作元素序列。它基于先进先出(First-In-First-Out, FIFO)原则,即最早入队的元素首先出队。只能在队尾添加元素,在队…...

被面试官问到分布式ID,别再傻乎乎只会答雪花算法了...
文章目录 1. 分布式ID2. 数据库主键自增3. 数据库号段模式4. Redis自增5. UUID6. Snowflake (雪花算法)7. Leaf (美团分布式ID生成系统)7.1 Leaf-segment 号段方案7.1.2 双buffer优化 7.2 Leaf-snowflake方案7.3 Leaf-snowflake Demo 1. 分布式ID 在分布式系统中,通…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
