Intellij 安装配置 lombok
Intellij 安装配置 lombok
用 lombok 能够减少 setter/getter/noArgsConstructor 这样的 boilerplate 代码,所以用起来还是比较方便的。
刚开始以为直接安装到 maven 里面就能用了,运行的时候发现 @Getter, @Data 这些 annotation 根本找不到,一查才发现原来配置没弄好,这里记一下配置的东西,以防之后换电脑还得继续找……
lombok 的官方网站为 https://projectlombok.org/,不过里面相对而言没什么内容
-
更新 POM
<dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><scope>provided</scope></dependency>如果要部署的话还是要注意一下这个
scope,provided 代表代表着在部署时,JDK 或者容器在运行时会提供该依赖,所以在 compile classpath 可以找到这个依赖,但是 runtime classpath 中不会所以如果打包的时候没有提供 lombok 插件,部署完的项目应该是没办法正常运行的
-
下载 lombok 插件
intellij 和 eclipse 中插件不一样,这里说 intellij,我用的插件是这个:
-
配置使用 annotation
这个需要到
> Settings > Build, Execution, Deployment > Compiler > Annotation Processors下面去开启: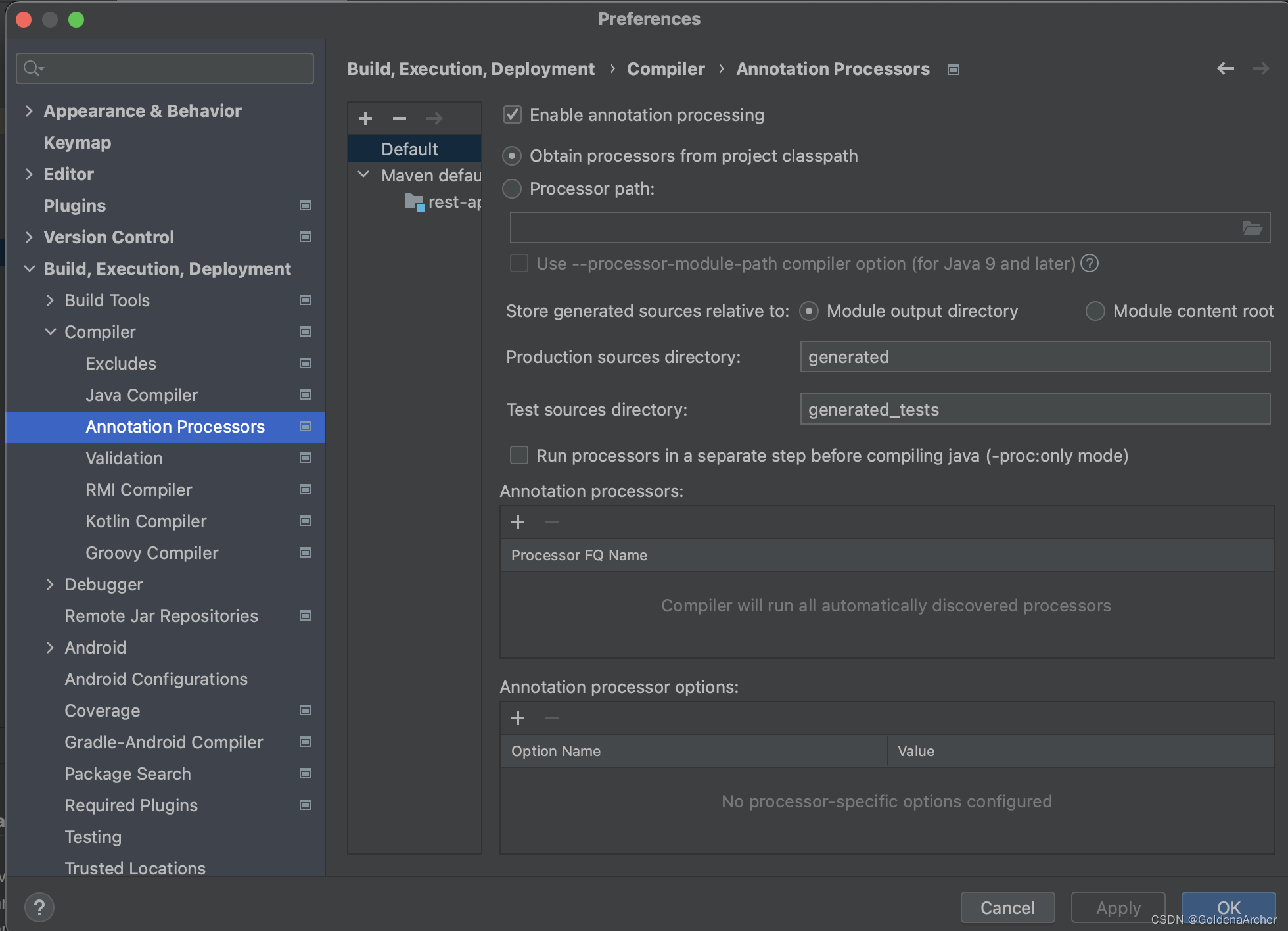
-
重新 build 一下
Intellij 上应该是会自动提示,说要将 lombok 添加到本地的 classpath 里面,如果失败的话也可以到终端使用
-U的 flag 强制更新一下
-
使用 lombok
package com.example.restapi.entity;import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;@Data @NoArgsConstructor @AllArgsConstructor public class Student {private String firstName;private String lastName; }需要注意的是,如果这里的 annotation 和实际的实现有冲突的话,intellij 就会报错:
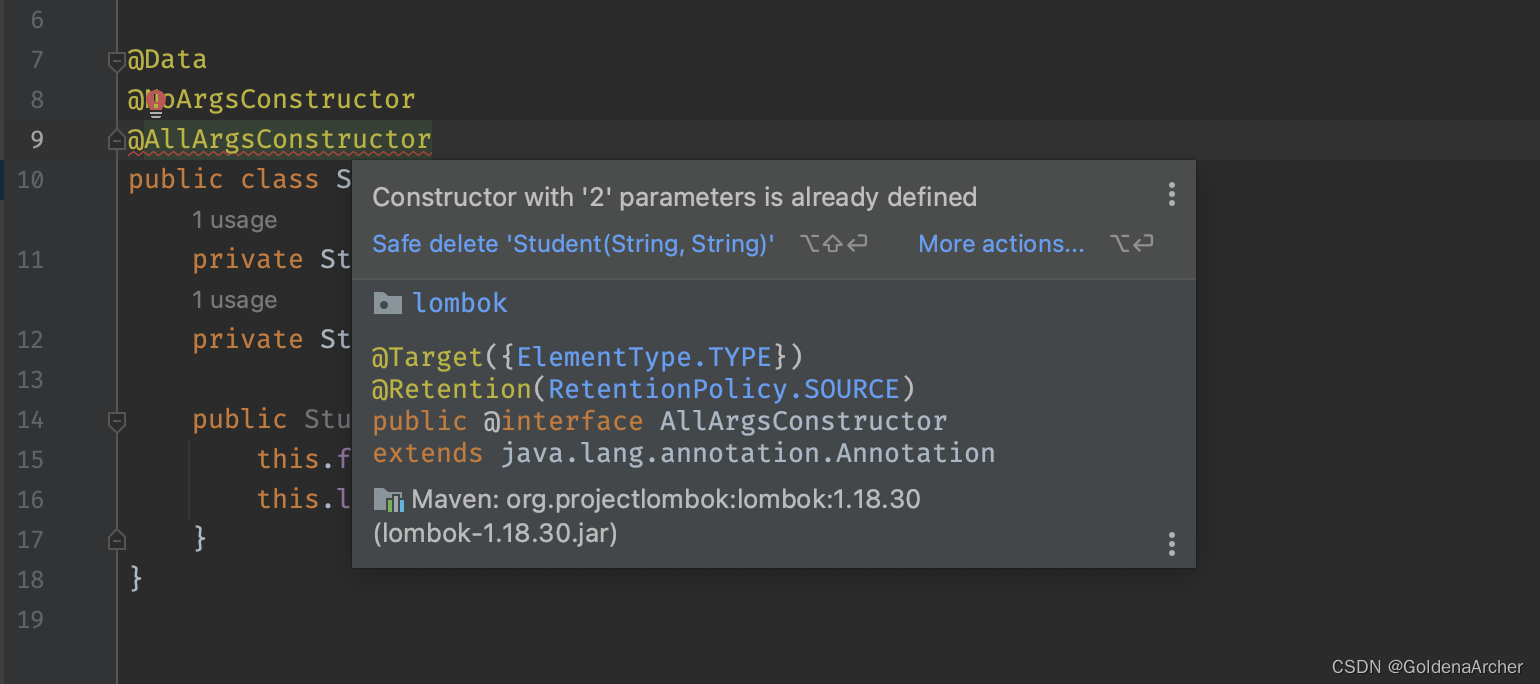
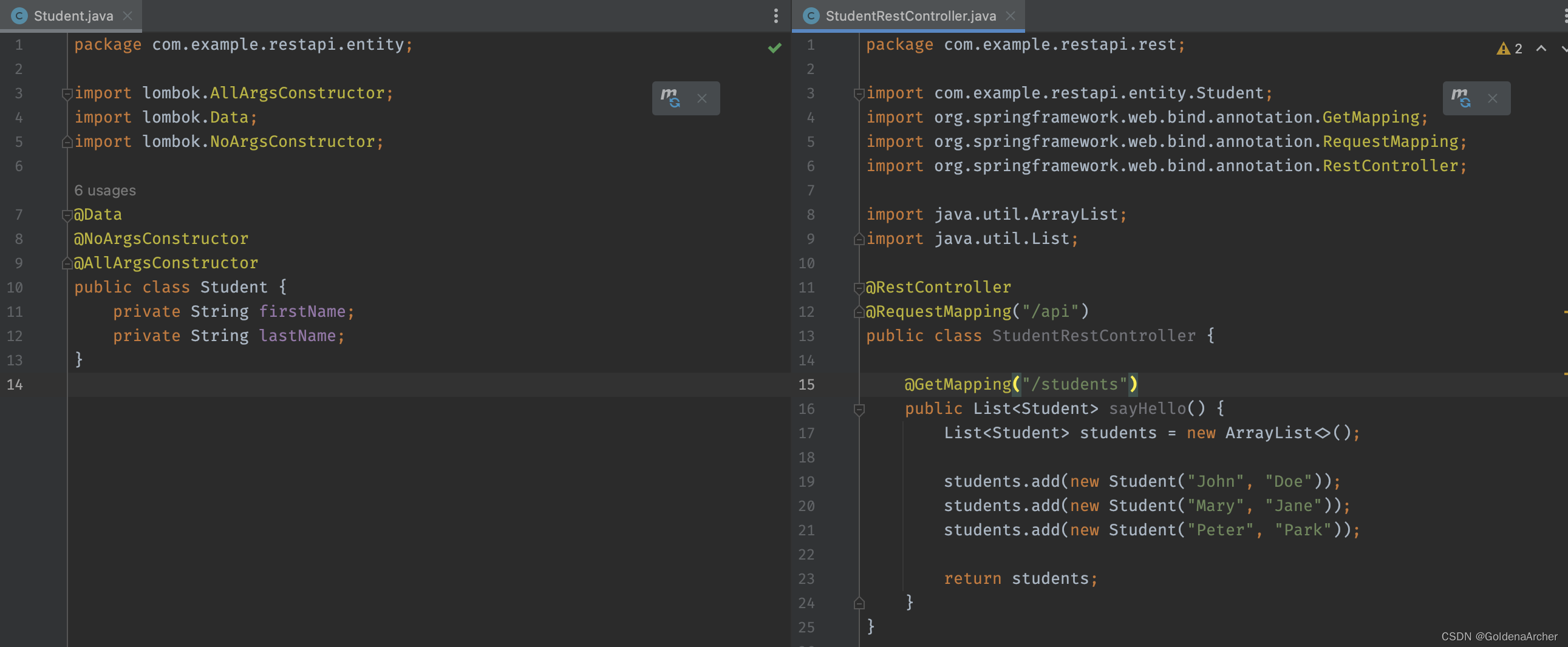
到这里 lombok 的配置就完成了,项目中也可以正常使用了:
参考
-
Adding Lombok plugin to IntelliJ project [duplicate]
-
lombok maven setup
这里有一些额外的资料,有需要的话可以参考一下
相关文章:

Intellij 安装配置 lombok
Intellij 安装配置 lombok 用 lombok 能够减少 setter/getter/noArgsConstructor 这样的 boilerplate 代码,所以用起来还是比较方便的。 刚开始以为直接安装到 maven 里面就能用了,运行的时候发现 Getter, Data 这些 annotation 根本找不到,…...

Chrome插件精选 — 暗色主题插件
Chrome实现同一功能的插件往往有多款产品,逐一去安装试用耗时又费力,在此为某一类型插件记录下比较好用的一款或几款,便于节省尝试的时间和精力。 Dark Reader 下载地址 (访问密码: 8276) Dark Reader是一款浏览器扩展程序,用于…...
PXE解决uefi安装centos6黑屏问题
解决pxe安装centos6黑屏 author: 铁乐与猫 date:2021.12.10 背景 主板:supermicr SBI-4129P-T3N System InformationManufacturer: SupermicroProduct Name: SBI-4129P-T3NVersion: 123456789Serial Number: S264322X9905439UUID: 00000000-0000-0000-0000-AC1…...

Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持?
Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持? 1.1 问题背景1.2 原因分析1.3 修复方案1.3.1 修复方案一 切换使用GET方法,可以试用多个SpringQueryMap注解 (测试实际不行)1.3.2 修复方案…...
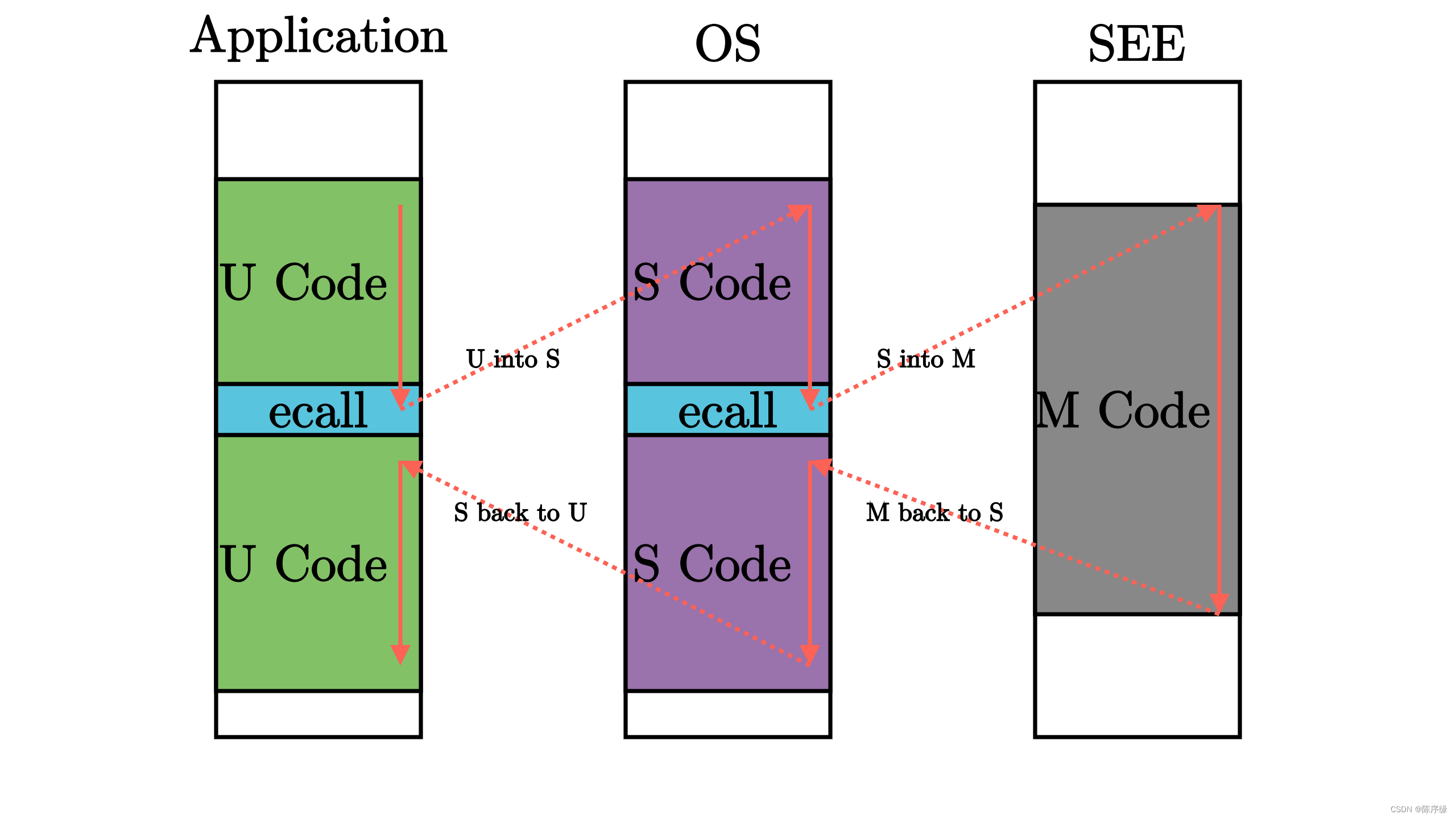
RISC-V 特权级架构
特权级别 级别的数值越大,特权级越高,掌控硬件的能力越强,在CPU硬件层面,M模式必须存在,其它模式可以不存在 执行环境调用 ecall ,这是一种很特殊的陷入类的指令, 相邻两特权级软件之间的接口正…...

目录启示:PHP 与命名空间的声明
文章目录 参考环境命名空间概念版本支持影响范围 全局命名空间概念魔术常量 \_\_NAMESPACE\_\_声明全局命名空间 声明命名空间为空间命名命名规则核心命名空间 子命名空间的声明在同一文件中定义多个命名空间无括号命名空间声明有括号命名空间声明禁止混合使用推荐使用有括号命…...
)
D. Divide and Equalize--Codeforces Round 903 (Div. 3)
D. Divide and Equalize 题意:让一组数中的一个数除以一个因子,一个数除以一个因子,假如经过若干次操作后能够使数组所有数相等,那么输出YES,否则输出NO。 分析:乘除因子,那么实际上就是因子的…...

保姆式教程:MAC安装Android studio(包括安装JDK,Android SDK),解决gradle下载慢的问题
文章目录 参考文章安装JDK并配置环境变量安装JDK配置JDK相关的环境变量 Android studio 安装下载Android studiogradle下载慢解决方法 安装Android SDK选择jdk版本安装SDK并配置环境变量 参考文章 原文链接 原文链接 安装JDK并配置环境变量 安装JDK 下载地址 下载后双击安装…...

Ps:选区的布尔运算
选区的布尔 Boolean运算指的是选区之间的相加(并集)、相减(差集)以及相交(交集),从而形成一个新的选区。 ◆ ◆ ◆ 使用工具选项栏 在 Ps 中,几乎所有的选区工具的工具选项栏上都有…...
PyTorch 深度学习之卷积神经网络(基础篇)Basic CNN(九)
0. Revision: Fully connected Neural Network 全连接 1. Convolution Neural Network 保留空间信息 1.1 Convolution Convolution-Single Input Channel 单通道 数乘 3 input Channels 3通道 N input Channels N input Channels and M output channel M 个卷积核 1.2 conv…...
torch实现Gated PixelCNN
文章目录 PixelCNNGated PixelCNN PixelCNN import torch import torch.nn as nn import torch.nn.functional as F# Pixel CNNclass MaskConv2d(nn.Module):def __init__(self, conv_type, *args, **kwags):super().__init__()assert conv_type in (A, B)self.conv nn.Conv2…...

破局「二次创业」:合思的新解法
在新的水温下,寻找更为良性的发展正在成为企业的必答题。对此,合思给出的不仅是一份更“省”的答题方法。也更是从认知层到行动层,最后到工具层的一张授人以渔的“渔网”。 作者|思杭 编辑|皮爷 出品|产业家 今年4月初,广州…...
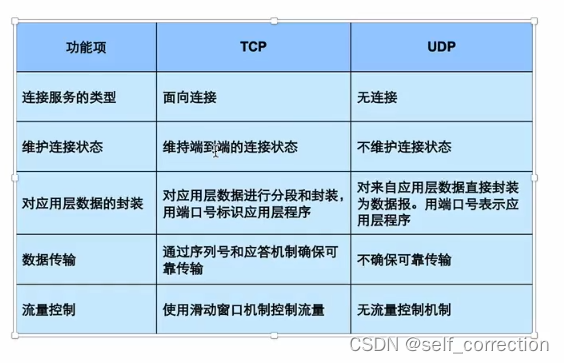
第五章:TCP和UDP基本原理
TCP和UDP基本原理 一、TCP/IP传输层的作用二、 端口1.范围2. 服务端3. 客户端4. 常见知名端口号4.1 TCP 80 HTTP4.2 TCP 20 21 FTP4.3 TCP 23 TELNET4.4 TCP 25 SMTP4.5 UDP 53 DNS4.6 TCP 443 HTTPS 三、 TCP原理1. TCP头部封装格式1.1 Source Port 源端口1.2 Destination Por…...

算法:动态规划的入门理解
文章目录 算法原理题目解析第n个泰波那契数列三步问题使用最小花费爬楼梯 从本篇开始总结的是动态规划的一些内容,动态规划是算法中非常重要的一个版块,因此也是学习算法中的一个重点,在学习动态规划前应当要把动态规划的基础知识学习一下 算…...

最新版nacos 2.2.3服务注册与发现版本依赖问题
最新版nacos的注册服务时配置文件写的是对的,但就是在nacos web页面无法看见服务,此时你需要注意你的依赖是否正确 spring: application:name: orderservicecloud:nacos:discovery:server-addr: 122.51.115.127:8848父工程依赖:现在最新的s…...
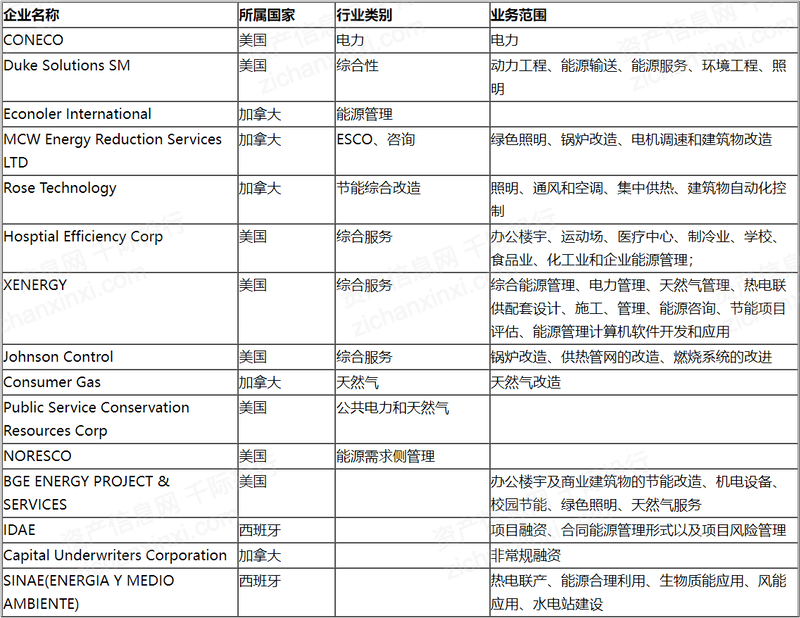
2023年中国合同能源管理行业研究报告
第一章 行业概况 1.1 定义及分类 合同能源管理 (Energy Performance Contracting, EPC) 是当前能源行业中一个重要的概念,它构建了一个桥梁,将节能服务公司 (Energy Management Company, EMCo) 与用能单位紧密联系在一起。通过特定的契约形式ÿ…...

php以半小时为单位,输出指定的时间范围
//可预订小时范围$hour [];for ($i$startHour*3600;$i<$endHour*3600;$i1800){//以半小时为单位输出$startHourItem date(H:i,strtotime(date(Y-m-d))$i);//小时开始$endHourItem date(H:i,strtotime(date(Y-m-d))$i1800);//当前时间再加半小时$hourItemStr $startHourI…...

Electron应用的 asar 打包 解压
前言: .asar文件是一种归档文件格式,通常用于封装Electron应用程序的资源。Electron是一个使得开发者能够使用Web技术构建跨平台桌面应用程序的框架。为了提高性能和简化部署,Electron应用程序的资源通常会被打包到一个.asar文件中。 安装 as…...

蓝桥等考Python组别十七级003
第一部分:选择题 1、Python L17 (15分) 运行下面程序,输出的结果是( )。 def func(x, y): return (x + y) // 3 print(func(7, 5)) 2468正确答案:B 2、Python L17 (15</...

Redis概述和与SpringBoot的整合
Redis是一种高性能的键值对存储数据库,它支持多种数据结构,包括字符串、哈希、列表、集合和有序集合等。Redis具有快速、可靠、灵活和可扩展等特点,也被广泛应用于缓存、队列和排行榜等场景。 SpringBoot是一种基于Spring框架的快速开发脚手…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
