linux中使用ps查看进程的所有线程
在 Linux 系统中,可以使用 ps 命令和 ps H 命令结合来查看进程的线程信息。ps 命令用于显示系统中当前运行的进程信息,而 ps H 命令则可以显示进程中的所有线程。
使用以下命令可以查看指定进程的所有线程信息:
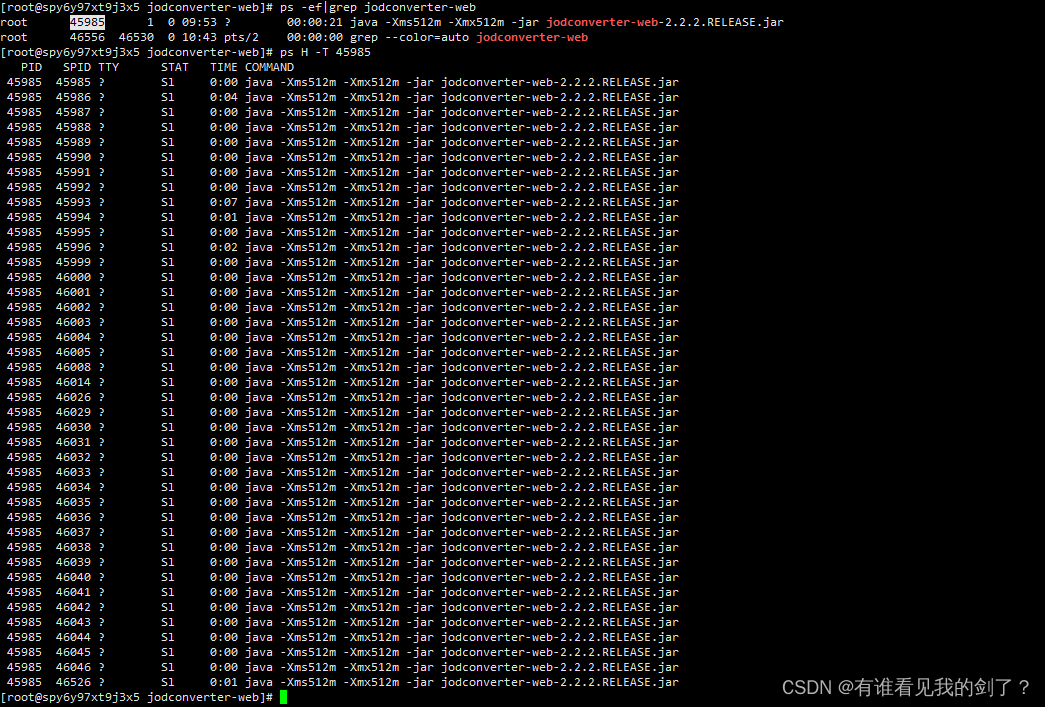
ps H -T <PID>
将 替换为要查看的进程的实际进程ID。
上述命令中,-T 选项用于显示进程的所有线程信息,而 -H 选项则用于列出线程信息时包含线程名(通常为进程名的缩写)。
该命令会输出进程的所有线程信息,包括线程ID、线程状态、CPU 使用率、内存占用等。这些信息可以用于诊断进程中的性能问题或其他故障。
需要注意的是,查看进程的所有线程信息可能需要以足够的权限运行 ps 命令,例如需要通过 sudo 或以超级用户身份运行该命令。另外,查看进程的线程信息可能会影响系统性能,因此在生产环境中应该谨慎使用,并根据需要进行过滤或筛选。
示例:
相关文章:

linux中使用ps查看进程的所有线程
在 Linux 系统中,可以使用 ps 命令和 ps H 命令结合来查看进程的线程信息。ps 命令用于显示系统中当前运行的进程信息,而 ps H 命令则可以显示进程中的所有线程。 使用以下命令可以查看指定进程的所有线程信息: ps H -T <PID>将 替换…...

本、硕、博区别真的辣么大吗?
61: 发际线已经说明了一切…… Super Mario: 小学,老师告诉学生:“森林里有只老虎,已经被我关在笼子里,我会带你去那个地方,然后给你一把猎枪,告诉你猎枪怎么用,并开枪…...

[Spring] SpringMVC 简介(一)
目录 一、SpringMVC 简介 1、什么是 MVC 2、什么是 SpringMVC 3、SpringMVC 实现原理 4、SpringMVC 的特点 二、简单案例 1、引入依赖 2、在 web.xml 中配置前端控制器 DispatcherServlet 3、创建 SpringMVC 的配置文件 4、创建请求控制器 5、测试页面 6、访问不到 …...
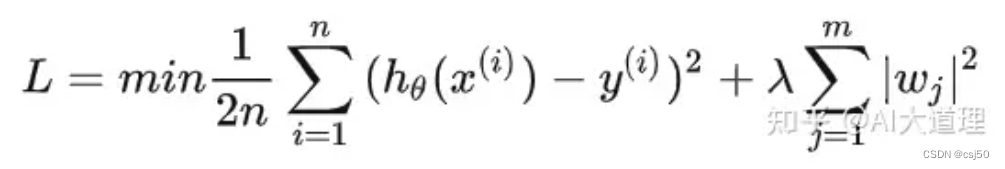
机器学习基础之《回归与聚类算法(2)—欠拟合与过拟合》
一、背景 1、上一篇说正规方程的时候,实际情况中使用很少,主要原因它不能解决过拟合。 2、训练集上表现的好,测试集上表现不好—过拟合 二、欠拟合和过拟合 1、欠拟合 训练集:有3个训练集,告诉机器都是天鹅 机器学…...
)
flutter dio 请求封装(空安全)
一、添加依赖 dio: ^5.3.2二、请求封装 class HttpHelper {static Dio? mDio;static BaseOptions? options;static HttpHelper? httpHelper;CancelToken cancelToken CancelToken();static const String GET get;static const String POST post;static const String PU…...

chatgpt GPT-4V是如何实现语音对话的
直接上代码 https://chat.openai.com/voice/get_token 1. 请求内容 Request:GET /voice/get_token HTTP/1.1 Host: ios.chat.openai.com Content-Type: application/json Cookie: _puiduser***Fc9T:16962276****Nph%2Fb**SU%3D; _uasid"Z0FBQUF***nPT0"; __cf_bmBUg…...

C++项目-求水仙花数
求水仙花数 #include <iostream> using namespace std;int main() {int n 100;do {int a 0;int b 0;int c 0;a n % 10; //个位b n / 10 % 10; //十位c n / 100 % 10; //百位if (a * a * a b * b * b c * c * c n) {cout << n << endl;}…...

从零开始基于LLM构建智能问答系统的方案
本文首发于博客 LLM应用开发实践 一个完整的基于 LLM 的端到端问答系统,应该包括用户输入检验、问题分流、模型响应、回答质量评估、Prompt 迭代、回归测试,随着规模增大,围绕 Prompt 的版本管理、自动化测试和安全防护也是重要的话题&#x…...

Android---Synchronized 和 ReentrantLock
Synchronized 基本使用 1. 修饰实例方法 public class SynchronizedMethods{private int sum 0;public synchronized void calculate(){sum sum 1;} } 这种情况下的锁对象是当前实例对象,因此只有同一个实例对象调用此方法才会产生互斥效果;不同的…...

【解题报告】牛客挑战赛70 maimai
题目链接 这个挑战赛的 F F F是我出的,最后 zhoukangyang 爆标了。。。orzorz 记所有有颜色的边的属性集合 S S S 。 首先在外层容斥,枚举 S ∈ [ 0 , 2 w ) S\in [0,2^w) S∈[0,2w),计算被覆盖的的边中不包含 S S S 中属性,…...

算启新程 智享未来 | 紫光展锐携手中国移动共创数智未来
10月11日-13日,2023年中国移动全球合作伙伴大会在广州举行,此次大会以“算启新程 智享未来”为主题,与合作伙伴一起共商融合创新,共创数智未来。作为中国移动每年规模最大、最具影响力的盛会,吸引了数百家世界500强企业…...
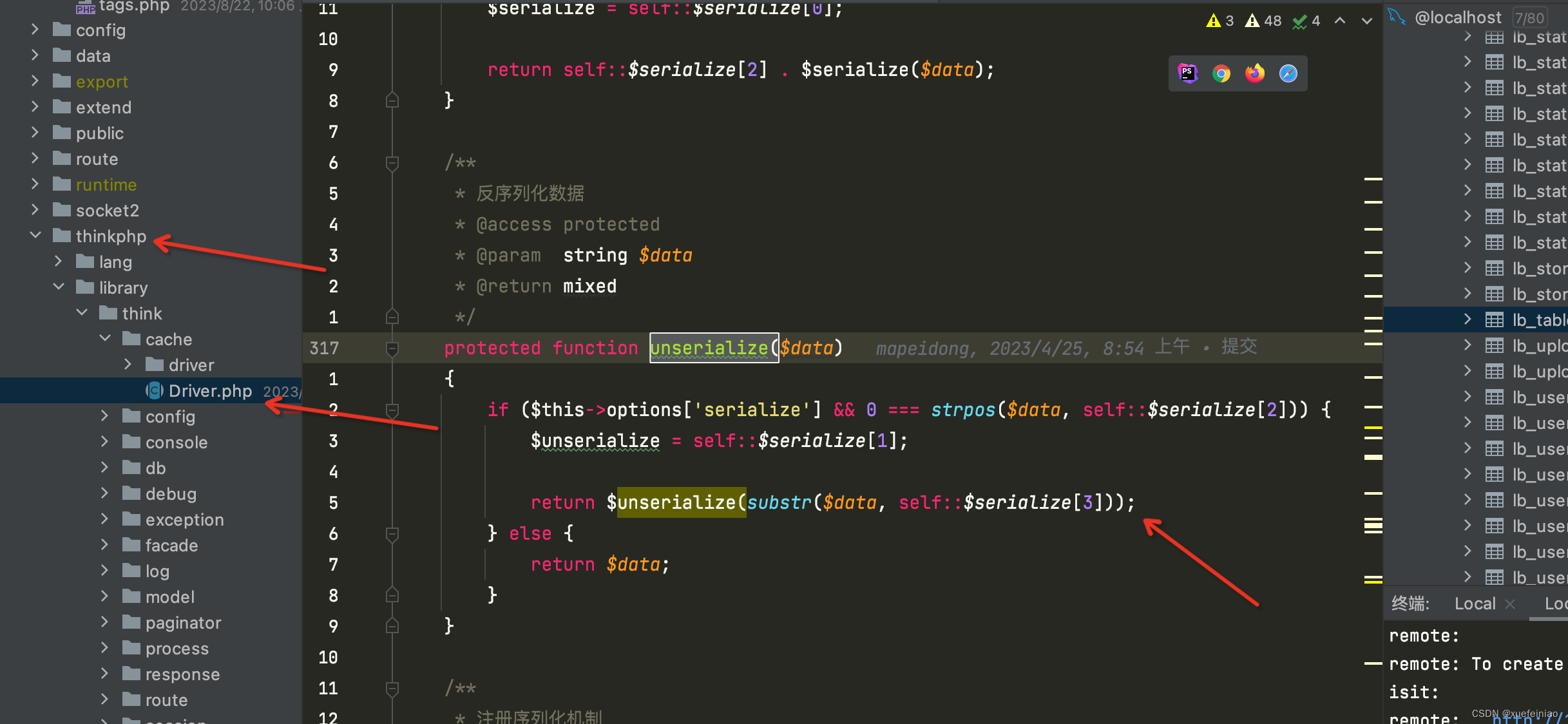
thinkphp5.1 获取缓存cache(‘cache_name‘)特别慢,php 7.0 unserialize 特别慢
thinkphp5.1 获取缓存cache(‘cache_name’)特别慢,php 7.0 unserialize 特别慢 场景: 项目中大量使用了缓存,本地运行非常快,二三百毫秒,部署到服务器后 一个表格请求就七八秒,最初猜想是数据库查询慢&am…...

【Linux】UNIX 术语中,换页与交换的区别和Linux 术语中,换页与交换的区别?
UNIX换页和交换的区别 在UNIX中,换页(Paging)是一种内存管理技术,用于在程序运行时动态地将其代码和数据从磁盘加载到内存中。当程序需要访问的页面不在内存中时,就会发生页错误(page error)&a…...

零基础学python之集合
文章目录 集合1、创建集合2、集合常见操作方法2、1 增加数据2、2 删除数据2、3 查找数据 3、总结 集合 目标 创建集合集合数据的特点集合的常见操作 1、创建集合 创建集合使用{}或set(), 但是如果要创建空集合只能使用set(),因为{}用来创建空字典。 …...

PromptScript:轻量级 DSL 脚本,加速多样化的 LLM 测试与验证
TL;DR 版本 PromptScript 是一个轻量级的 Prompt 调试用的 DSL (Yaml)脚本,以用于快速使用、构建 Prompt。 PromptScript 文档:https://framework.unitmesh.cc/prompt-script Why PromptScript ? 几个月前&…...

强化学习(Reinforcement Learning)与策略梯度(Policy Gradient)
写在前面:本篇博文的内容来自李宏毅机器学习课程与自己的理解,同时还参考了一些其他博客(懒得放链接)。博文的内容主要用于自己学习与记录。 1 强化学习的基本框架 强化学习(Reinforcement Learning, RL)主要由智能体(Agent/Actor)、环境(Environment)、…...

JUC之ForkJoin并行处理框架
ForkJoin并行处理框架 Fork/Join 它可以将一个大的任务拆分成多个子任务进行并行处理,最后将子任务结果合并成最后的计算结果,并进行输出。 类似于mapreduce 其实,在Java 8中引入的并行流计算,内部就是采用的ForkJoinPool来实现…...

【牛客面试必刷TOP101】Day8.BM33 二叉树的镜像和BM36 判断是不是平衡二叉树
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:牛客面试必刷TOP101 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&…...
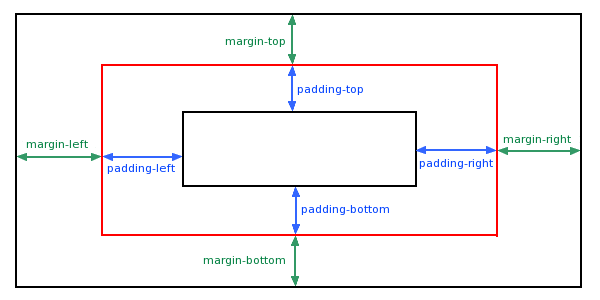
CSS padding(填充)
CSS padding(填充)是一个简写属性,定义元素边框与元素内容之间的空间,即上下左右的内边距。 padding(填充) 当元素的 padding(填充)内边距被清除时,所释放的区域将会受到…...
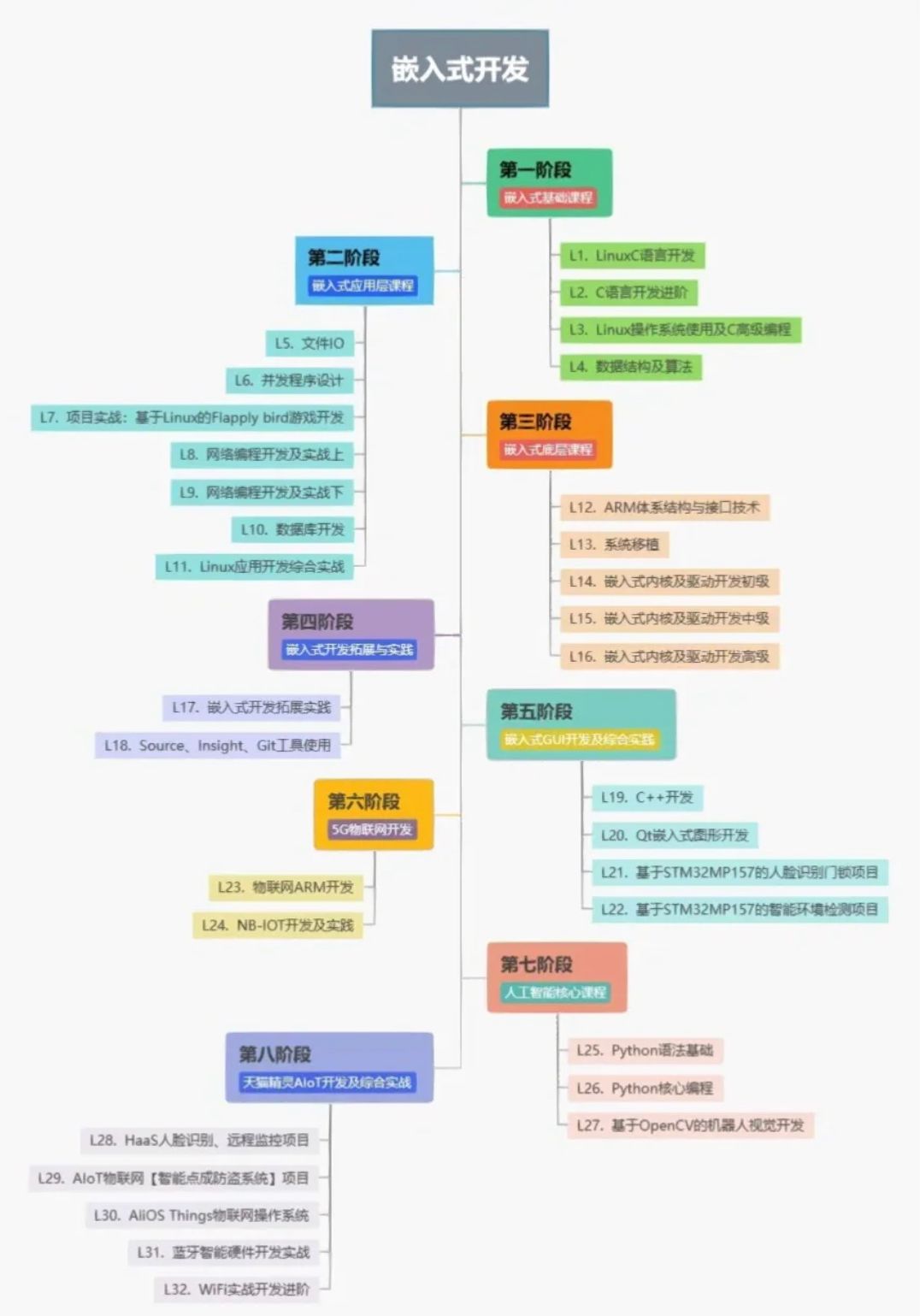
C语言达到什么水平才能从事单片机工作
C语言达到什么水平才能从事单片机工作 从事单片机工作需要具备一定的C语言编程水平。以下是几个关键要点:基本C语言知识: 掌握C语言的基本语法、数据类型、运算符、流控制语句和函数等基本概念。最近很多小伙伴找我,说想要一些C语言学习资料&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
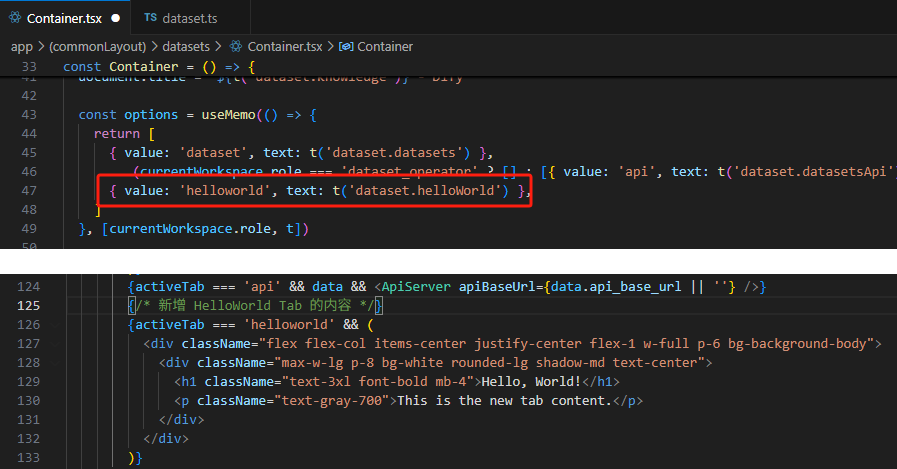
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...

JS面试常见问题——数据类型篇
这几周在进行系统的复习,这一篇来说一下自己复习的JS数据结构的常见面试题中比较重要的一部分 文章目录 一、JavaScript有哪些数据类型二、数据类型检测的方法1. typeof2. instanceof3. constructor4. Object.prototype.toString.call()5. type null会被判断为Obje…...

Java多线程从入门到精通
一、基础概念 1.1 进程与线程 进程是指运行中的程序。 比如我们使用浏览器,需要启动这个程序,操作系统会给这个程序分配一定的资源(占用内存资源)。 线程是CPU调度的基本单位,每个线程执行的都是某一个进程的代码的某…...
