强化学习(Reinforcement Learning)与策略梯度(Policy Gradient)
写在前面:本篇博文的内容来自李宏毅机器学习课程与自己的理解,同时还参考了一些其他博客(懒得放链接)。博文的内容主要用于自己学习与记录。
1 强化学习的基本框架
强化学习(Reinforcement Learning, RL)主要由智能体(Agent/Actor)、环境(Environment)、状态(State)、动作(Action)、奖励(Reward)组成。在这些成员中,需要训练的是智能体,他会根据不同的状态产生动作。具体过程见下图,智能体由环境得到Observation(状态),再根据Observation得到一个动作作用于环境产生一个新的环境,再根据之前的状态和动作会给出奖励(正奖励或者负奖励)。随后,智能体根据新的状态和奖励,按照一定的策略执行新的动作。智能体通过强化学习,可以知道自己在什么状态下,应该采取什么样的动作使得自身获得最大奖励。

2 强化学习基本步骤
2.1 步骤1:构建决策框架
对于智能体(后文都用Actor)模块,很容易想到构建一个用于分类任务的Neural Network,根据例如图像一类的输入,通过Neural Network的计算得到每个动作的概率,选最大概率的动作作为最终的动作。再根据最终的Reward进行反向传播更新权重,从而达到训练的效果。这是典型的Deep Learning(DL)做法。当然,在RL中确实是这么做的。

有了可训练的网络模型,就需要定义"Loss Function"用于训练。不同的是DL是为了使结果更加精准,需要尽可能的减小Loss,是一个“下山”的过程,而RL是为了尽可能的增大奖励,是一个“上山”的过程。奖励可以根据动作和状态计算,例如下图中击杀怪物后会获得一定量的分数。

让模型不断产生动作直到游戏结束,这就是一轮次(episode)(类似于DL中的epoch),那么我们可以把所有的奖励累加起来。一个简单的思路是可以利用奖励和去更新Neural Network的权重。

定义:一次episode的奖励总和为 R = ∑ t = 1 T r t R=\sum_{t=1}^{T}{r_t} R=∑t=1Trt ,总共进行 T T T 次动作, r t r_t rt 为第 t t t 次动作 a T a_T aT 产生的奖励。现在需要训练Neural Network使 R R R 最大化,这就需要一个优化策略。
2.2 Policy Gradient详解
怎么知道这个动作好还是不好呢?可以让Actor实际的去“玩”一下游戏。假设动作 π θ ( s ) \pi_\theta(s) πθ(s) 的参数是 θ \theta θ ,就让Actor π θ ( s ) \pi_\theta(s) πθ(s) 反复去玩这个游戏。那么经过不断“玩”,可以得到总得分为 R θ R_\theta Rθ 。就算是在同一个环境下采取相同的Action,得到的 R θ R_\theta Rθ 也会不相同,这是因为Actor具有一定的随机性。那么我们需要尽可能大的去增加总奖励的期望 R ˉ θ \bar R_\theta Rˉθ ,而不是某一次的结果增大。

定义:一次episode的所有状态、动作、奖励组成的向量叫 τ \tau τ ,其代表一次episode的过程,相关公式如下:
τ = { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . , s T , a T , r T } \tau = \{s1, a1, r1, s2, a2, r2, ..., s_T, a_T, r_T\} τ={s1,a1,r1,s2,a2,r2,...,sT,aT,rT}
R ( τ ) = ∑ n = 1 N r n R(\tau)=\sum_{n=1}^{N}r_n R(τ)=n=1∑Nrn
假设对于一个Actor,每一种过程 τ \tau τ 都可能被列举到,每一种 τ \tau τ 出现的概率取决于Actor的参数 θ \theta θ ,定义为 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 。那么 R ˉ θ \bar R_\theta Rˉθ 就等于每一次episode中的得分 R θ R_\theta Rθ 与该过程 τ \tau τ 出现的几率的乘积之和,见如下公式:
R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) \bar R_\theta=\sum_{\tau}{R(\tau)P(\tau|\theta)}\approx\frac{1}{N}\sum_{n=1}^N{R(\tau^n)} Rˉθ=τ∑R(τ)P(τ∣θ)≈N1n=1∑NR(τn)
但 τ \tau τ 的情况太复杂了,难以枚举所有情况,可以让 π θ \pi_\theta πθ sample N N N 次,得到 { τ 1 , τ 2 , . . . , τ N } \{\tau^1, \tau^2, ..., \tau^N\} {τ1,τ2,...,τN} 与所有的出现概率 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 。那么问题就变成了如下表达式:
θ ∗ = arg max θ R ˉ θ , R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) \theta^{*}=\arg \max _{\theta} \bar{R}_{\theta}, \bar{R}_{\theta}=\sum_{\tau}R(\tau)P(\tau|\theta) θ∗=argθmaxRˉθ,Rˉθ=τ∑R(τ)P(τ∣θ)
由前文中提到RL的训练过程是一个“上山”的过程,所以可以用Gradient Ascent。
2.2.1 Gradient Ascent
需要更新的权重为 θ \theta θ ,梯度的方向为 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ 。

根据 R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) \bar{R}_{\theta}=\sum_{\tau}R(\tau)P(\tau|\theta) Rˉθ=∑τR(τ)P(τ∣θ) ,其中 R ( τ ) R(\tau) R(τ) 由于其有一定的随机性,只需要把 τ \tau τ 放进去根据 R ( ⋅ ) R(·) R(⋅) 得到结果,可以把其看成一个完全的“黑盒子”,不用考虑其可微性质。这样考虑的具体原因是 R ( τ ) R(\tau) R(τ) 本身是由环境打分得到的,环境是一个“黑盒子”。那么 ∇ R θ \nabla R_{\theta} ∇Rθ 为:
∇ R θ = ∑ τ R ( τ ) ∇ P ( τ ∣ θ ) = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ P ( τ ∣ θ ) P ( τ ∣ θ ) \nabla R_\theta = \sum_{\tau}{R(\tau)\nabla P(\tau|\theta)} = \sum_{\tau}{R(\tau)P(\tau|\theta)\frac{\nabla P(\tau|\theta)}{P(\tau|\theta)}} ∇Rθ=τ∑R(τ)∇P(τ∣θ)=τ∑R(τ)P(τ∣θ)P(τ∣θ)∇P(τ∣θ)
又由于:
d l o g ( f ( x ) ) d x = 1 f ( x ) d f ( x ) d x \frac{dlog(f(x))}{dx}=\frac{1}{f(x)} \frac{df(x)}{dx} dxdlog(f(x))=f(x)1dxdf(x)
∇ l o g ( f ( x ) ) = ∇ f ( x ) f ( x ) \nabla log(f(x))=\frac{\nabla f(x)}{f(x)} ∇log(f(x))=f(x)∇f(x)
那么 ∇ R θ \nabla R_\theta ∇Rθ 可以变为:
∇ R θ = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ l o g P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ l o g P ( τ n ∣ θ ) \nabla R_\theta = \sum_{\tau}{R(\tau)P(\tau|\theta)\nabla log P(\tau|\theta)} \approx \frac{1}{N}\sum^{N}_{n=1}{R(\tau^n)\nabla log P(\tau^n|\theta)} ∇Rθ=τ∑R(τ)P(τ∣θ)∇logP(τ∣θ)≈N1n=1∑NR(τn)∇logP(τn∣θ)
其中 “玩” N N N 次游戏得到 { τ 1 , τ 2 , . . . , τ N } \{\tau^1, \tau^2, ..., \tau^N\} {τ1,τ2,...,τN} ,假设 N N N 足够大,表示概率的部分 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 就可以直接利用平均数去掉。现在的问题变成了如何计算 ∇ l o g P ( τ ∣ θ ) \nabla log P(\tau|\theta) ∇logP(τ∣θ) 。
我们可以把 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 展开:
P ( τ ∣ θ ) = p ( s 1 ) p ( a 1 ∣ s 1 , θ ) p ( r 1 , s 2 ∣ s 1 , a 1 ) p ( a 2 ∣ s 2 , θ ) p ( r 2 , s 3 ∣ s 2 , a 2 ) ⋯ = p ( s 1 ) ∏ t = 1 T p ( a t ∣ s t , θ ) p ( r t , s t + 1 ∣ s t , a t ) P(\tau|\theta)= p\left(s_{1}\right) p\left(a_{1} \mid s_{1}, \theta\right) p\left(r_{1}, s_{2} \mid s_{1}, a_{1}\right) p\left(a_{2} \mid s_{2}, \theta\right) p\left(r_{2}, s_{3} \mid s_{2}, a_{2}\right) \cdots =p(s_1)\prod^{T}_{t=1}{p(a_t|s_t, \theta)p(r_t, s_{t+1}|s_t, a_t)} P(τ∣θ)=p(s1)p(a1∣s1,θ)p(r1,s2∣s1,a1)p(a2∣s2,θ)p(r2,s3∣s2,a2)⋯=p(s1)t=1∏Tp(at∣st,θ)p(rt,st+1∣st,at)
其实这是一个用于描述马尔科夫决策过程的公式,其中每个状态和行动都有相应的概率分布。其中 p ( s 1 ) p(s_1) p(s1) 与 p ( r t , s t + 1 ∣ s t , a t ) p(r_t, s_{t+1}|s_t, a_t) p(rt,st+1∣st,at) 跟 π θ \pi_\theta πθ 是没关系的, p ( a t ∣ s t , θ ) p(a_t|s_t, \theta) p(at∣st,θ) 受 π θ \pi_\theta πθ 控制,后者的解释可以见下图。

那么 l o g P ( τ ∣ θ ) logP(\tau|\theta) logP(τ∣θ) 可以变成如下:
l o g P ( τ ∣ θ ) = l o g p ( s 1 ) + ∑ t = 1 T l o g p ( a t ∣ s t , θ ) + l o g p ( r t , s t + 1 ∣ s t , a t ) logP(\tau|\theta) = logp(s_1)+\sum_{t=1}^{T}logp(a_t|s_t, \theta) + logp(r_t, s_{t+1}|s_t, a_t) logP(τ∣θ)=logp(s1)+t=1∑Tlogp(at∣st,θ)+logp(rt,st+1∣st,at)
则 ∇ l o g P ( τ ∣ θ ) \nabla log P(\tau|\theta) ∇logP(τ∣θ) 跟 π θ \pi_\theta πθ 不相干的项直接可以去掉了,变成如下式子:
∇ l o g P ( τ ∣ θ ) = ∑ t = 1 T ∇ l o g p ( a t ∣ s t , θ ) \nabla logP(\tau|\theta)=\sum_{t=1}^{T}\nabla logp(a_t|s_t, \theta) ∇logP(τ∣θ)=t=1∑T∇logp(at∣st,θ)
那么可以把这个式子往回带,就可以得到 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ (注意这里的 T T T 变成了 T n T_n Tn ,这是因为对于不同的 τ \tau τ 产生动作序列的次数不一样,所以需要添加下标 n n n 与 不同轮次的 τ \tau τ 对应):
∇ R ˉ θ ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ l o g P ( τ n ∣ θ ) = 1 N ∑ n = 1 N R ( τ θ ) ∑ t = 1 T n ∇ l o g p ( a t n ∣ s t n , θ ) = 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ θ ) ∇ l o g p ( a t n ∣ s t n , θ ) \nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^{N}{R(\tau^n) \nabla log P(\tau^n|\theta)} = \frac{1}{N} \sum_{n=1}^{N}{R(\tau^\theta) \sum_{t=1}^{T_n}{\nabla log p(a_t^n|s_t^n, \theta)}} = \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n}{R(\tau^\theta){\nabla log p(a_t^n|s_t^n, \theta)}} ∇Rˉθ≈N1n=1∑NR(τn)∇logP(τn∣θ)=N1n=1∑NR(τθ)t=1∑Tn∇logp(atn∣stn,θ)=N1n=1∑Nt=1∑TnR(τθ)∇logp(atn∣stn,θ)
这个式子的含义是,假设在sample的一个 θ \theta θ 里面, s t n s_t^n stn 这个State下采取了 a t n a_t^n atn 这个动作的概率,取log再计算梯度,与那一次 τ \tau τ 的总奖励相乘。进一步理解,如果在某一次 τ n \tau^n τn 时,机器在看到状态 s t n s_t^n stn 时,采取了一个动作 a t n a_t^n atn ,然后总的奖励是正的,那么机器就会自己去增加看到这个场景下做出该行动的概率。

值得注意的是,如果把梯度里的 R ( τ n ) R(\tau^n) R(τn) 替换成 r t n r_t^n rtn 后,也就是将第 n n n 次 τ n \tau^n τn 的总奖励换成第 n n n 次 τ n \tau^n τn 在 t t t 时刻在状态 s t n s_t^n stn 下采取动作 a t n a_t^n atn 得到的奖励,那么就会丢失其他动作的期望贡献,最后训练出来的模型只会在原地开火。这里还能这么理解(个人理解),如果换成 r t n r_t^n rtn ,由于sample的随机性,可以不用考虑 1 N ∑ n = 1 N \frac{1}{N}\sum_{n=1}^{N} N1∑n=1N 这一层。那么 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ 可以写成:
∇ R ˉ θ = g ( ∑ t = 1 T r t ∇ l o g p ( a t ∣ s t , θ ) ) \nabla \bar R_\theta = g(\sum_{t=1}^{T}r_t \nabla log p(a_t|s_t, \theta)) ∇Rˉθ=g(t=1∑Trt∇logp(at∣st,θ))
此时的 r t r_t rt 与 a t , s t a_t, s_t at,st 唯一对应,那么梯度在每个时刻只关注了一个动作的奖励与概率~~,很容易陷入局部最优~~,导致训练出来的模型在某一特定环境下只会侧重一个动作。由Actor在不同连续的 s t s_t st 下产生的一系列动作是有一定的关联性的~~,类似于NLP上下文特征或者音频里的时域特征~~,所以不能只考虑某一 a t , s t a_t, s_t at,st 下单独的 r t r_t rt。这就有点类似于分类任务的损失函数。
有了梯度,就可以根据Gradient Ascent更新Actor网络的权重,公式如下:
θ n e w ← θ o l d + η ∇ R ˉ θ o l d \theta^{new} ← \theta^{old} + \eta \nabla \bar R_{\theta^{old}} θnew←θold+η∇Rˉθold
下面我们再看看更新模型的过程,如下图,即生成一组训练数据,更新一次 θ \theta θ ,值得注意的是每一组训练数据只能用一次。

2.2.2 如何损失函数进一步优化
假设所有的 R ( τ n ) R(\tau^n) R(τn) 都是正值。假设在某一个状态下,采取 a , b , c a, b, c a,b,c 三个动作的概率如下,但 a , c a, c a,c 的奖励更高,那么理想状态下经过训练 a , c a, c a,c 出现的概率会增高, b b b 出现的概率会降低。但实际上我们是sample的,假设没有采集到 a a a 动作这种情况,那么经过训练后 a a a 出现的概率会降低。这时,我们需要引入一个baseline,即可以对 R ( τ n ) R(\tau^n) R(τn) 减去一个 b b b ,从而使奖励有好有坏,不然都是正值无法区分,通常可以将 b b b 值设置为与 R ( τ n ) R(\tau^n) R(τn) 的期望接近的值,即 E [ R ( τ n ) ] E[R(\tau^n)] E[R(τn)]。

还有很多方法能缓解这一问题,例如为不同的动作分配不同的权重,即好的动作给正分,差的动作给负分,再将 R ( τ n ) R(\tau^n) R(τn) 替换成所有动作的权重和,这种做法的本质就是改变了原本奖励的计算。

随着时间的推移,状态-动作的组合会越来越多,那么前面的组合对距离过远的组合的影响就会越来越小,可以用添加一个衰减因子 γ \gamma γ ,这种方法叫Advantage function,见下图。

相关文章:

强化学习(Reinforcement Learning)与策略梯度(Policy Gradient)
写在前面:本篇博文的内容来自李宏毅机器学习课程与自己的理解,同时还参考了一些其他博客(懒得放链接)。博文的内容主要用于自己学习与记录。 1 强化学习的基本框架 强化学习(Reinforcement Learning, RL)主要由智能体(Agent/Actor)、环境(Environment)、…...

JUC之ForkJoin并行处理框架
ForkJoin并行处理框架 Fork/Join 它可以将一个大的任务拆分成多个子任务进行并行处理,最后将子任务结果合并成最后的计算结果,并进行输出。 类似于mapreduce 其实,在Java 8中引入的并行流计算,内部就是采用的ForkJoinPool来实现…...

【牛客面试必刷TOP101】Day8.BM33 二叉树的镜像和BM36 判断是不是平衡二叉树
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:牛客面试必刷TOP101 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&…...
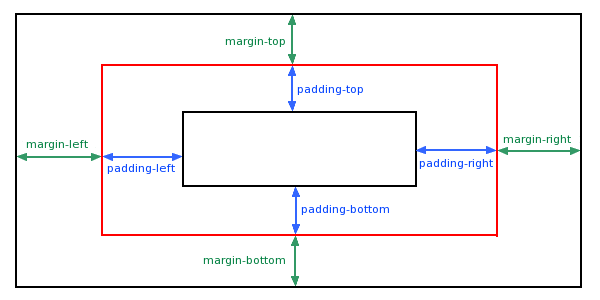
CSS padding(填充)
CSS padding(填充)是一个简写属性,定义元素边框与元素内容之间的空间,即上下左右的内边距。 padding(填充) 当元素的 padding(填充)内边距被清除时,所释放的区域将会受到…...
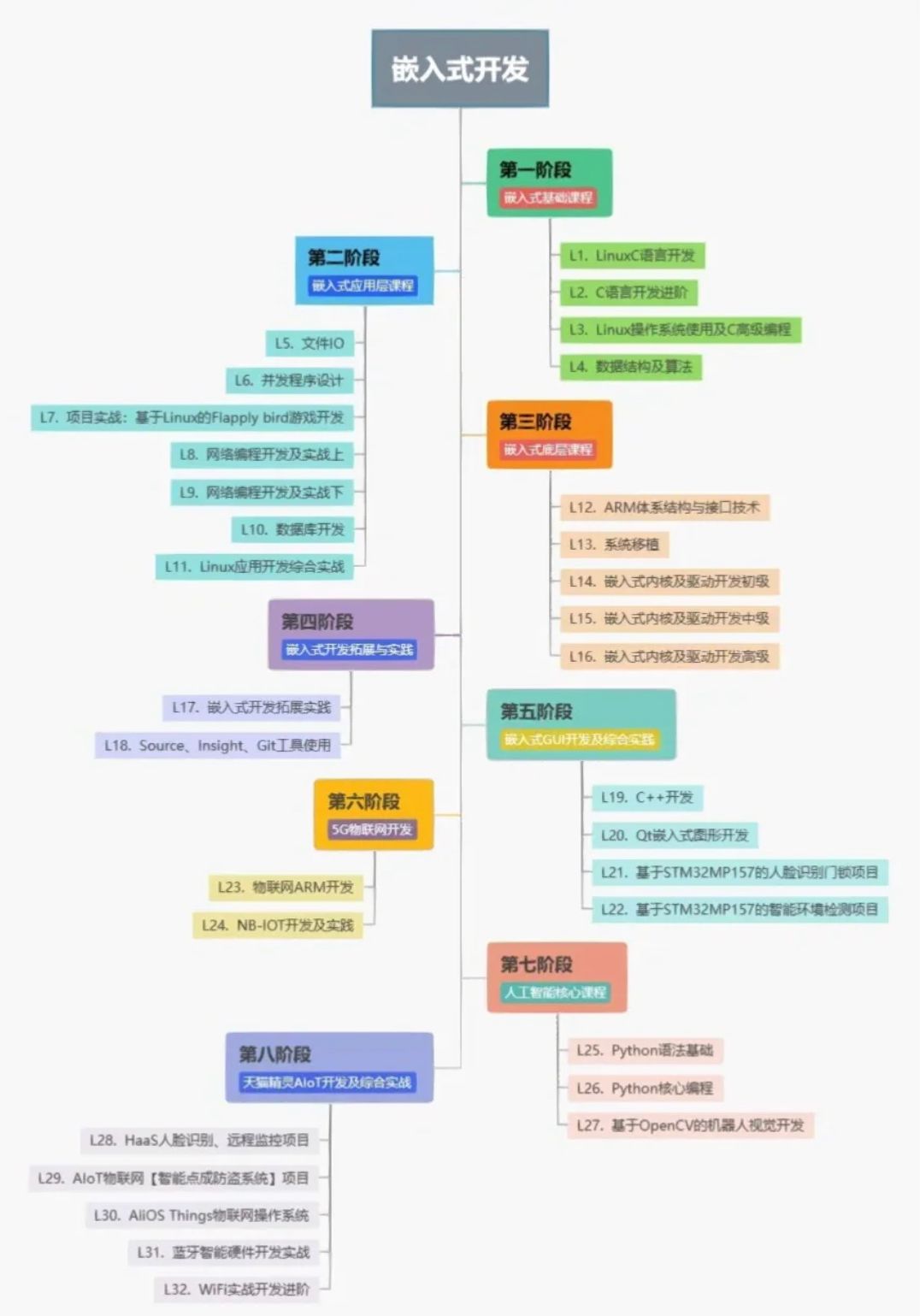
C语言达到什么水平才能从事单片机工作
C语言达到什么水平才能从事单片机工作 从事单片机工作需要具备一定的C语言编程水平。以下是几个关键要点:基本C语言知识: 掌握C语言的基本语法、数据类型、运算符、流控制语句和函数等基本概念。最近很多小伙伴找我,说想要一些C语言学习资料&…...

Java架构师理解SAAS和多租户
目录 1 云服务的三种模式1.1 IaaS(基础设施即服务)1.2 PaaS(平台即服务)1.3 SaaS(软件即服务)1.4 区别与联系2 SaaS的概述2.1 Saas详解2.2 应用领域与行业前景2.3 Saas与传统软件对比3 多租户SaaS平台的数据库方案3.1 多租户是什么3.2 需求分析3.3 多租户的数据库方案分析…...
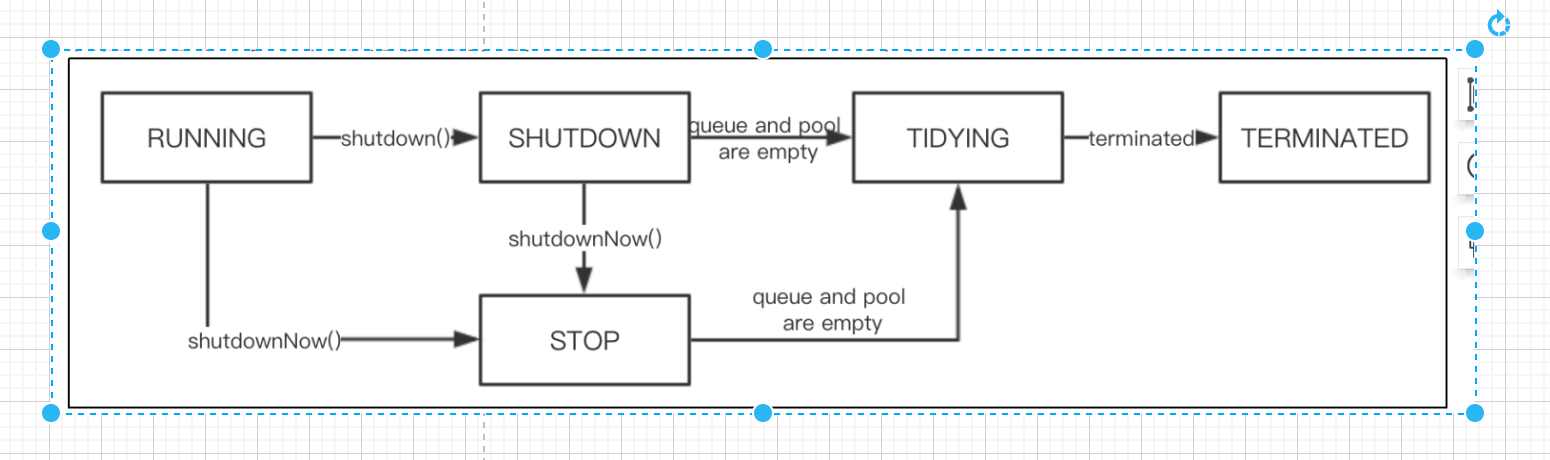
关于Java线程池相关面试题
【更多面试资料请加微信号:suns45】 https://flowus.cn/share/f6cd2cbe-627a-435f-a6e5-1395333f92e8 【FlowUs 息流】📣suns-Java资料 访问密码:【请加微信号:suns45】 ————线程相关的面试题———— 0:创建线…...
ExcelBDD Python指南
在Python里面支持BDD Excel BDD Tool Specification By ExcelBDD Method This tool is to get BDD test data from an excel file, its requirement specification is below The Essential of this approach is obtaining multiple sets of test data, so when combined with…...

基于深度学习的驾驶员疲劳监测系统的设计与实现
点击以下链接获取源码: https://download.csdn.net/download/qq_64505944/88421622?spm1001.2014.3001.5503 基于深度学习的驾驶员疲劳监测系统的设计与实现 1 绪论 在21世纪,各国的经济飞速发展,人民越来越富裕,道路上的汽车也逐…...
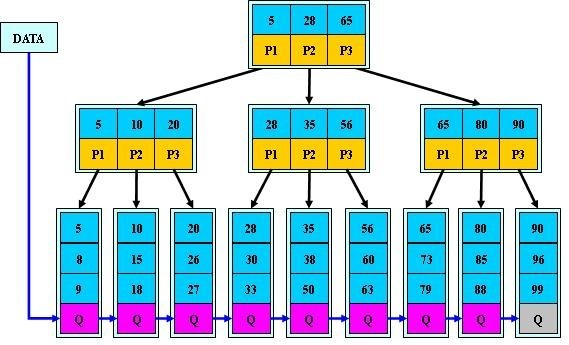
B树、B+树详解
B树 前言 首先,为什么要总结B树、B树的知识呢?最近在学习数据库索引调优相关知识,数据库系统普遍采用B-/Tree作为索引结构(例如mysql的InnoDB引擎使用的B树),理解不透彻B树,则无法理解数据…...
使用hugging face开源库accelerate进行多GPU(单机多卡)训练卡死问题
目录 问题描述及配置网上资料查找1.tqdm问题2.dataloader问题3.model(input)写法问题4.环境变量问题 我的卡死问题解决方法 问题描述及配置 在使用hugging face开源库accelerate进行多GPU训练(单机多卡)的时候,经常出现如下报错 [E Process…...
IDEA 修改插件安装位置
不说假话,一定要看到最后,不然你以为我为什么要自己总结!!! IDEA 修改插件安装位置 前言步骤 前言 IDEA 默认的配置文件均安装在C盘,使用时间长会生成很多文件,这些文件会占用挤兑C盘空间&…...

牛客网SQL160
国庆期间每类视频点赞量和转发量_牛客题霸_牛客网 select * from ( select tag,dt, sum(单日点赞量)over(partition by tag order by dt rows between 6 preceding and 0 following), max(单日转发量)over(partition by tag order by dt rows between 6 preceding and 0 follo…...
HDFS Java API 操作
文章目录 HDFS Java API操作零、启动hadoop一、HDFS常见类接口与方法1、hdfs 常见类与接口2、FileSystem 的常用方法 二、Java 创建Hadoop项目1、创建文件夹2、打开Java IDEA1) 新建项目2) 选择Maven 三、配置环境1、添加相关依赖2、创建日志属性文件 四、Java API操作1、在HDF…...
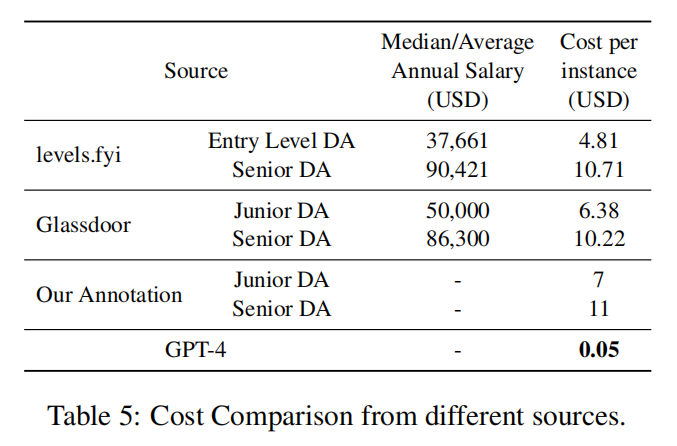
论文阅读之【Is GPT-4 a Good Data Analyst?(GPT-4是否是一位好的数据分析师)】
文章目录 论文阅读之【Is GPT-4 a Good Data Analyst?(GPT-4是否是一位好的数据分析师)】背景:数据分析师工作范围基于GPT-4的端到端数据分析框架将GPT-4作为数据分析师的框架的流程图 实验分析评估指标表1:GPT-4性能表现表2&…...
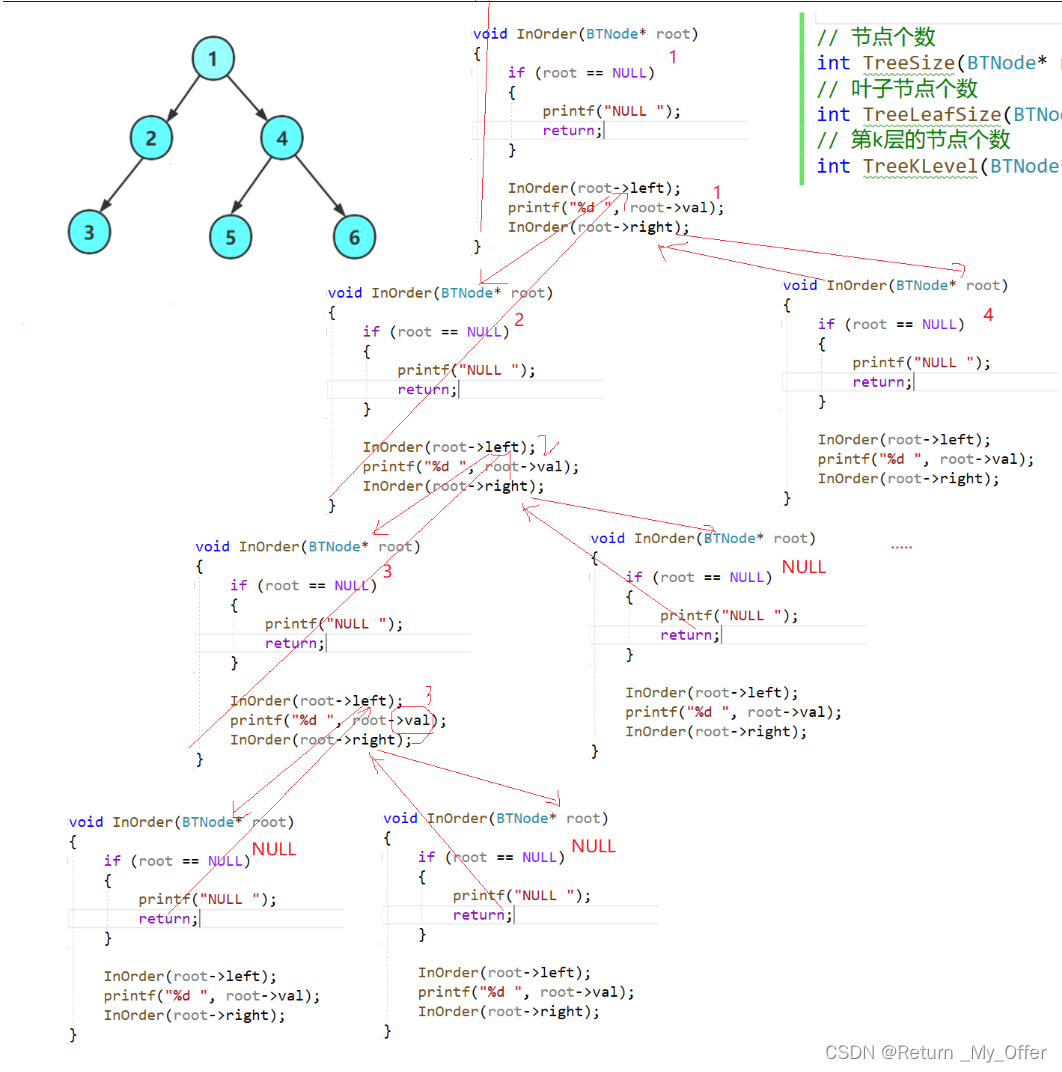
【数据结构】:二叉树与堆排序的实现
1.树概念及结构(了解) 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的有一个特殊的结点&#…...

纯css手写switch
CSS 手写switch 纯css手写switchcss变量 纯css手写switch 思路: switch需要的元素有:开关背景、开关按钮。点击按钮后,背景色变化,按钮颜色变化,呈现开关打开状态。 利用typecheckbox,来实现switch效果(修…...

PyTorch 深度学习之处理多维特征的输入Multiple Dimension Input(六)
1.Multiple Dimension Logistic Regression Model 1.1 Mini-Batch (N samples) 8D->1D 8D->2D 8D->6D 1.2 Neural Network 学习能力太好也不行(学习到的是数据集中的噪声),最好的是要泛化能力,超参数尝试 Example, Arti…...

LeetCode【438】找到字符串中所有字母异位词
题目: 注意:下面代码勉强通过,每次都对窗口内字符排序。然后比较字符串。 代码: public List<Integer> findAnagrams(String s, String p) {int start 0, end p.length() - 1;List<Integer> result new ArrayL…...
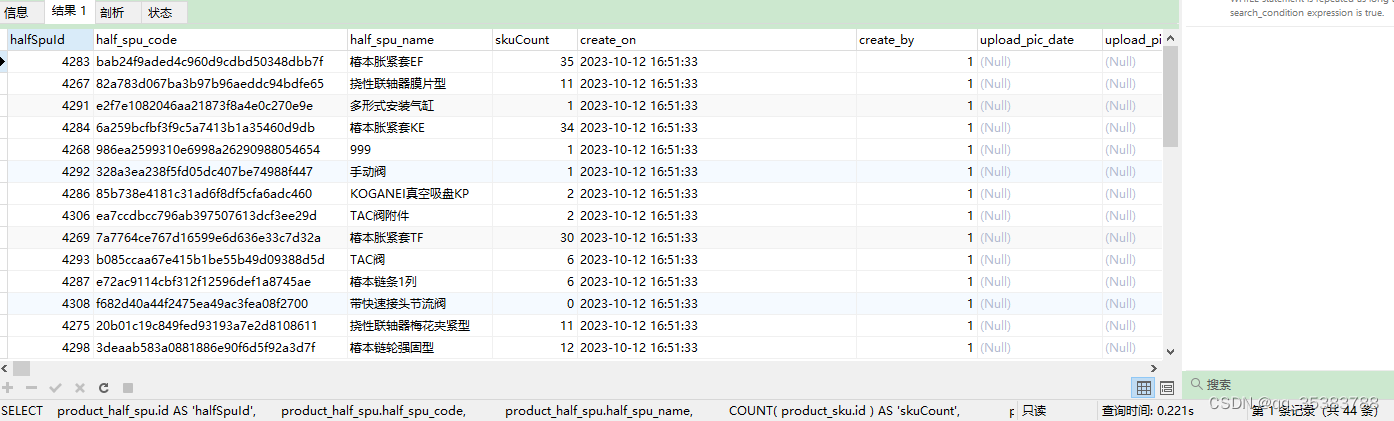
关于LEFT JOIN的一次理解
先看一段例子: SELECTproduct_half_spu.id AS halfSpuId,product_half_spu.half_spu_code,product_half_spu.half_spu_name,COUNT( product_sku.id ) AS skuCount,product_half_spu.create_on,product_half_spu.create_by,product_half_spu.upload_pic_date,produc…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
