【数据结构】:二叉树与堆排序的实现

1.树概念及结构(了解)
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的

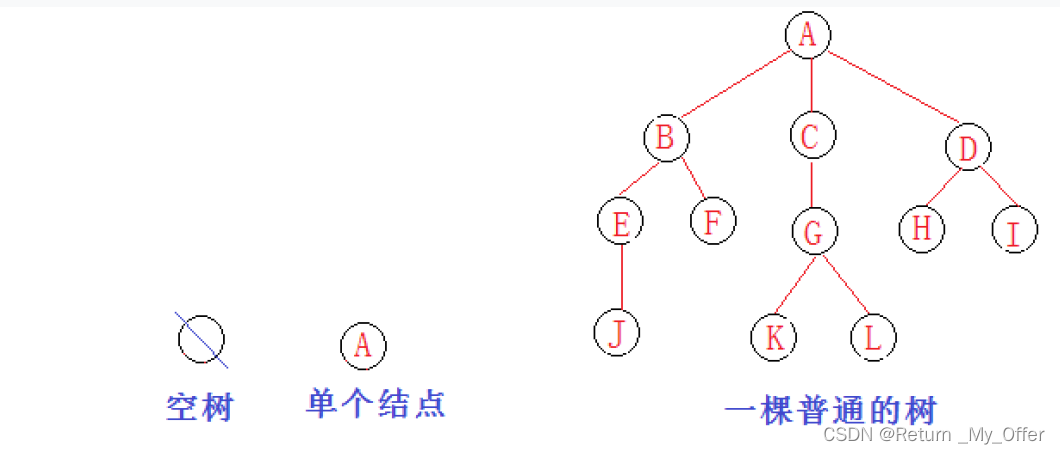
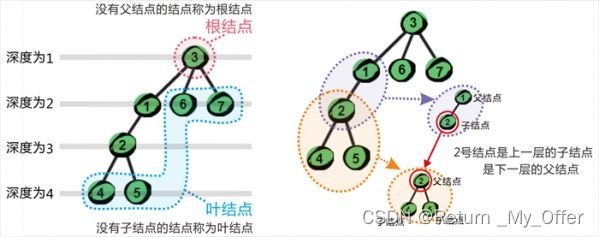
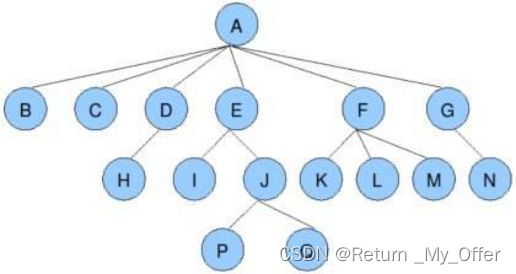
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)
1.2树的表示
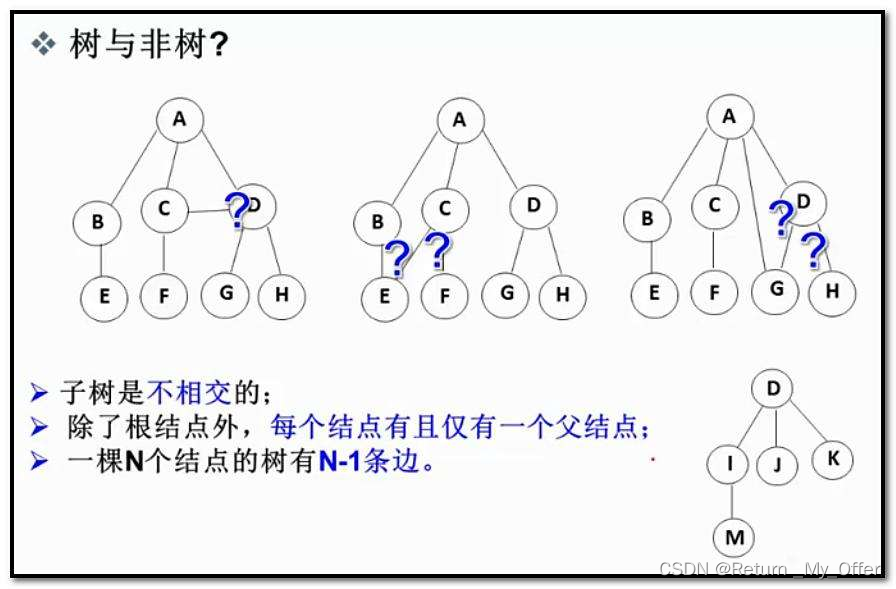
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,
如:双亲表示法,孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子
兄弟表示法
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
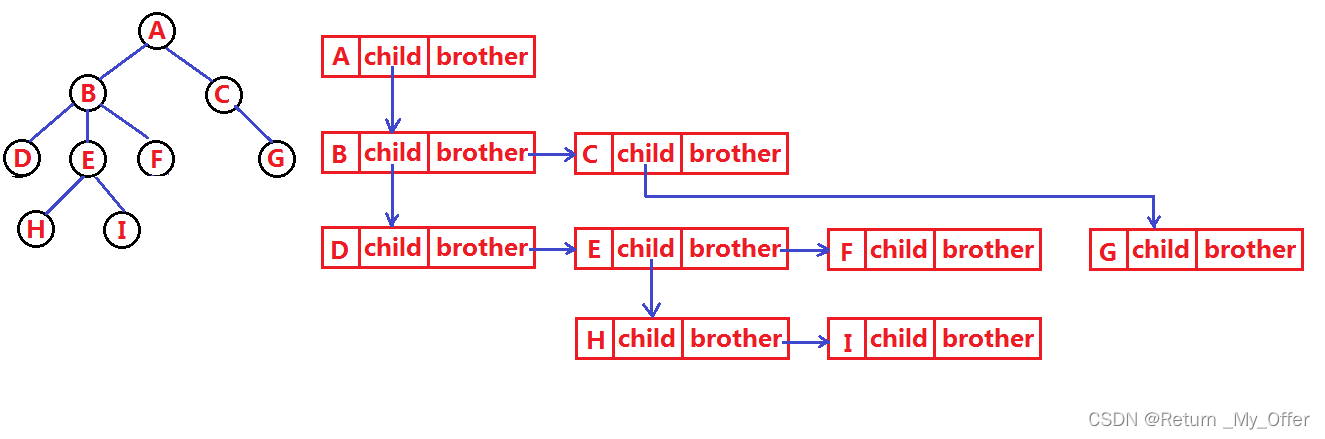
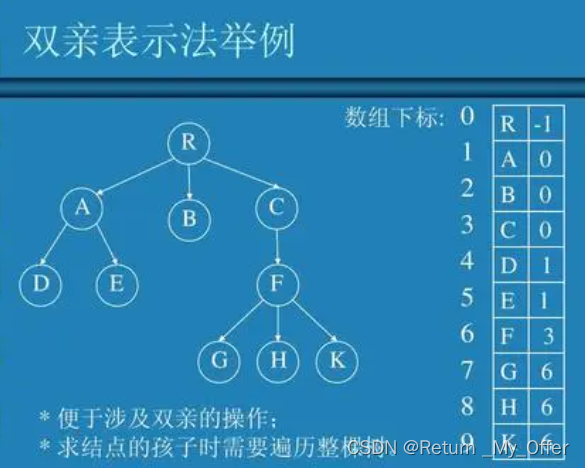
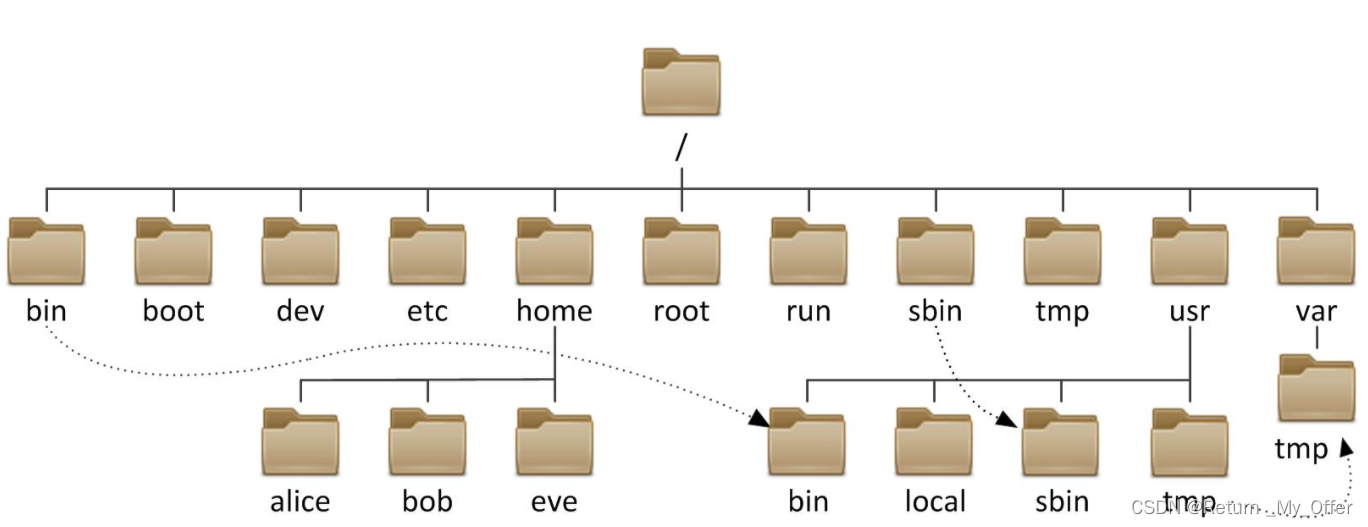
注意:在Linux中我们能够输入tree指令把我们电脑中的文件以多叉树的形式呈现
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子
树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
2.2现实中的二叉树:


2.3数据结构中的二叉树:
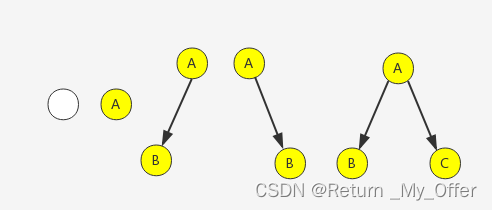
2.4特殊的二叉树:
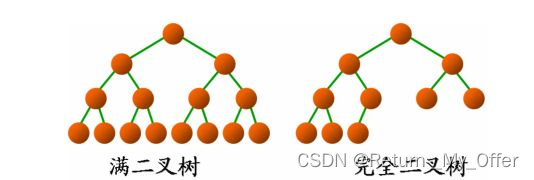
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树
2.5 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2+1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=LogN
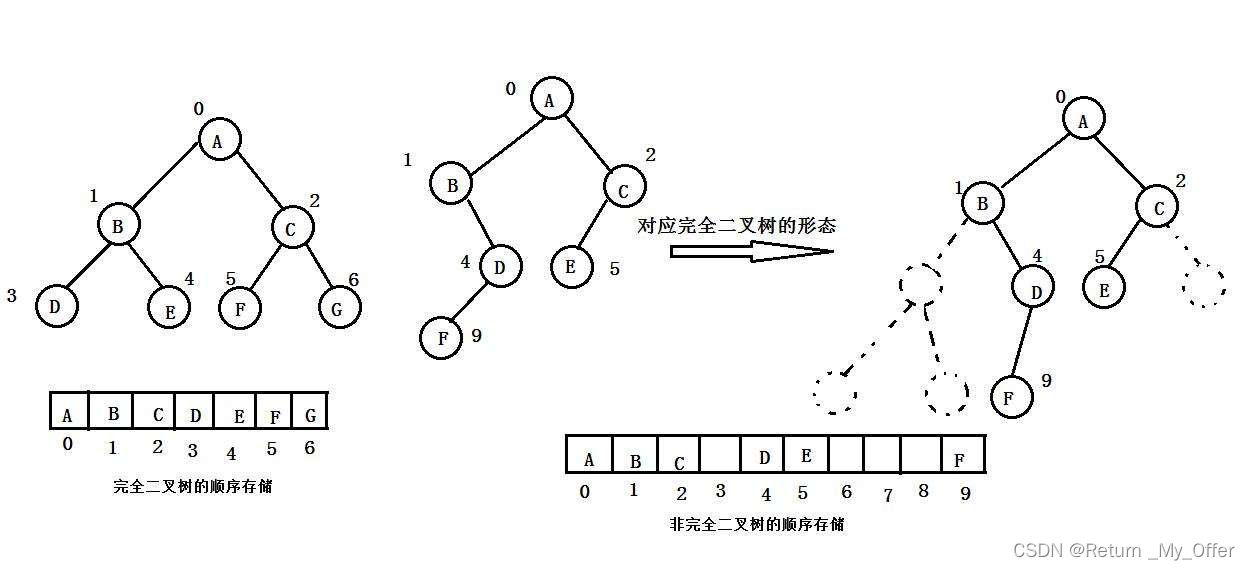
2.5.1 顺序存储:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
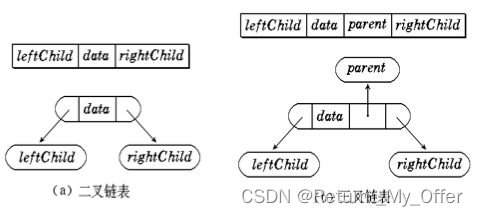
2.5.2 链式存储:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链
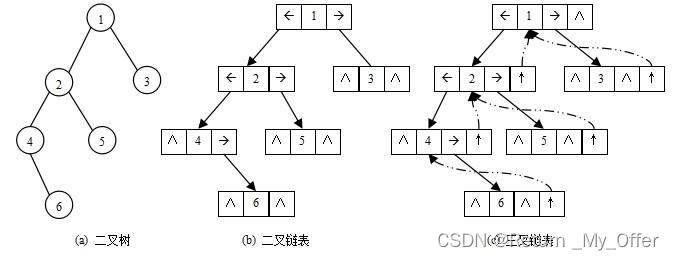
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* pParent; // 指向当前节点的双亲struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
3.二叉树链式结构的实现
3.1二叉树链式结构的遍历
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础
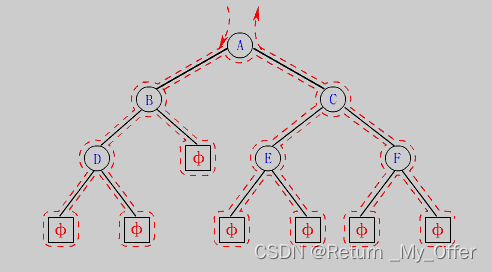
前序/中序/后序的递归结构遍历:是根据访问结点操作发生位置命名
- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前
- LNR:中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)
- LRN:后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历
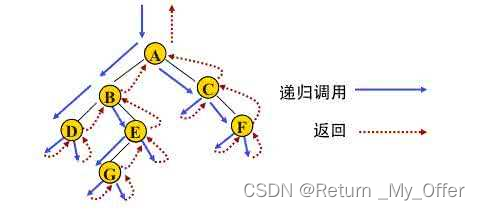

层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的
根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然
后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问
树的结点的过程就是层序遍历
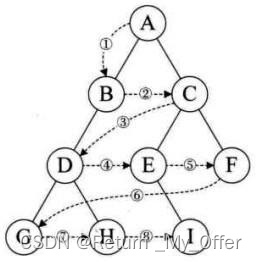
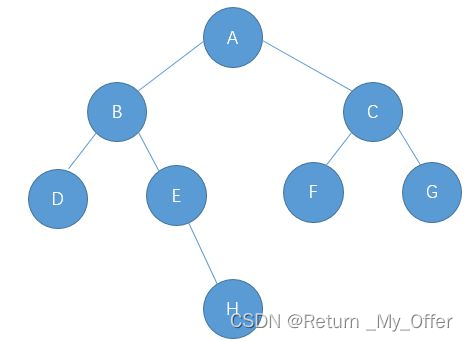
练习:请写出下面的前序/中序/后序/层序遍历
实现推排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种 它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆
遵循最大堆与最小堆的原则
最大堆:每个节点的值都大于或者等于他的左右孩子节点的值
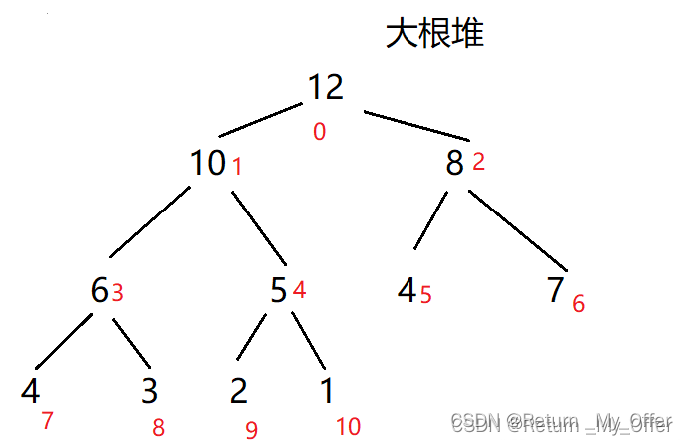
最小堆:每个节点的值都大于或者等于他的左右孩子节点的值
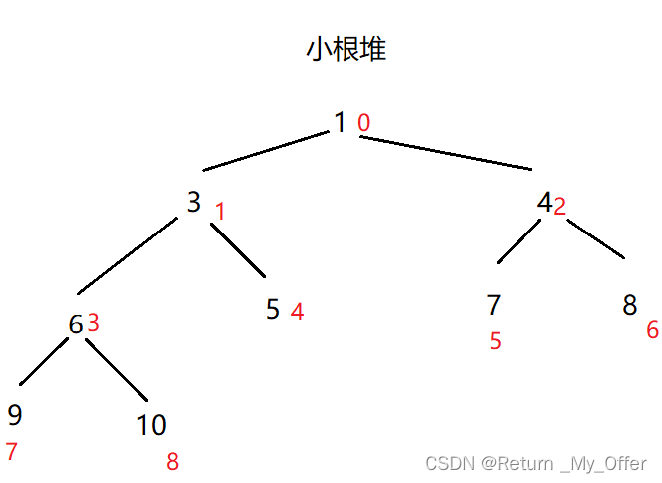
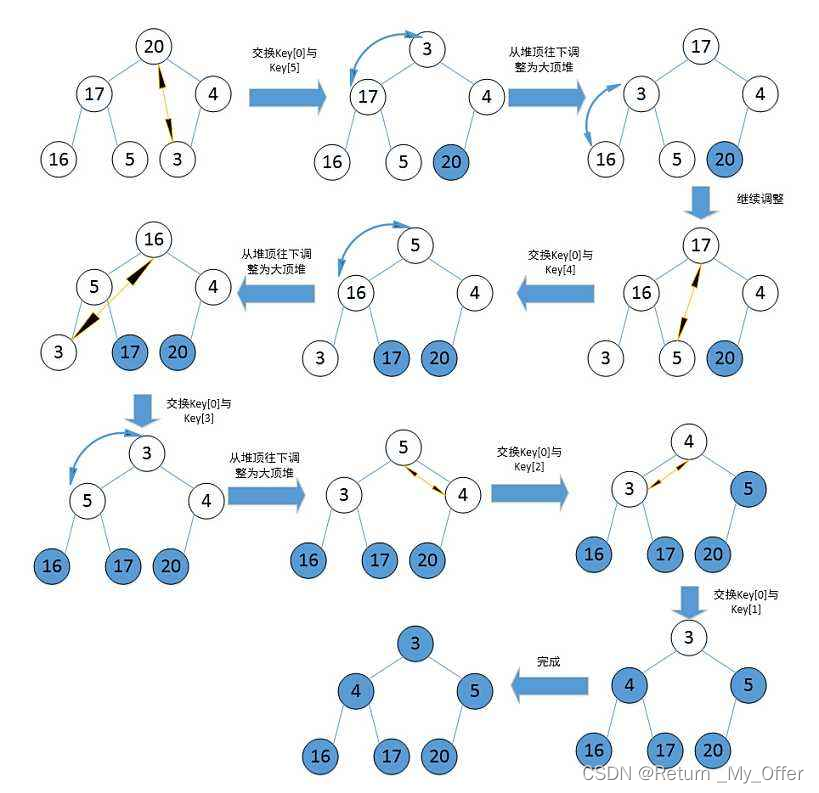
- 堆排序使用堆来选数,效率就高了很多
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
堆排序总的代码的实现
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;HPDataType _size;HPDataType _capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
bool HeapEmpty(HP* php);
HPDataType HeapTop(HP* php);
#include"Heap.h"
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->_size = 0;php->_capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->_size = 0;php->_capacity = 0;
}void AdJustUP(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);//C语言交换函数可自行尝试解决child = parent;parent = (parent - 1) / 2;}else {break;}}
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->_capacity == php->_size){int NewCapacity = php->_capacity = 0 ? 4 : php->_capacity * 2;HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * NewCapacity);if (temp == NULL) {perror("realloc fail");exit(-1);}php->a = temp;php->_capacity = NewCapacity;}php->a[php->_size] = x;php->_size++;AdJustUP(php->a, php->_size - 1);
}void HeapPop(HP* php)
{assert(php);assert(php->_size > 0);Swap(&php->a[0], &php->a[php->_size - 1]);--php->_size;AdjustDown(php->a, php->_size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->_size > 0);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->_size == 0;
}

这里涉及一些数学知识 稍微想一下就能够理解各位老铁 等差数列和等比数列的知识
实现二叉树
#include<stdio.h>
#include<stdlib.h>// 不是增删查改,学习二叉树结构
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}void PrevOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}// 节点个数
//int TreeSize(BTNode* root)
//{
// static int size = 0;
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}//int size = 0;
//int TreeSize(BTNode* root)
//{
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}// 叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}// 第k层的节点个数
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1){return 1;}return TreeKLevel(root->left, k - 1)+ TreeKLevel(root->right, k - 1);
}int main()
{// 手动构建BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;PrevOrder(node1);printf("\n");InOrder(node1);printf("\n");PostOrder(node1);printf("\n");printf("%d\n", TreeSize(node1));//size = 0;printf("%d\n", TreeSize(node1));return 0;
}
二叉树的本质是递归
这里二叉树的遍历又分为前中后序遍历
前面的图片已经给大家呈现出来了
下面给大家画一个二叉树前序遍历的递归展开图
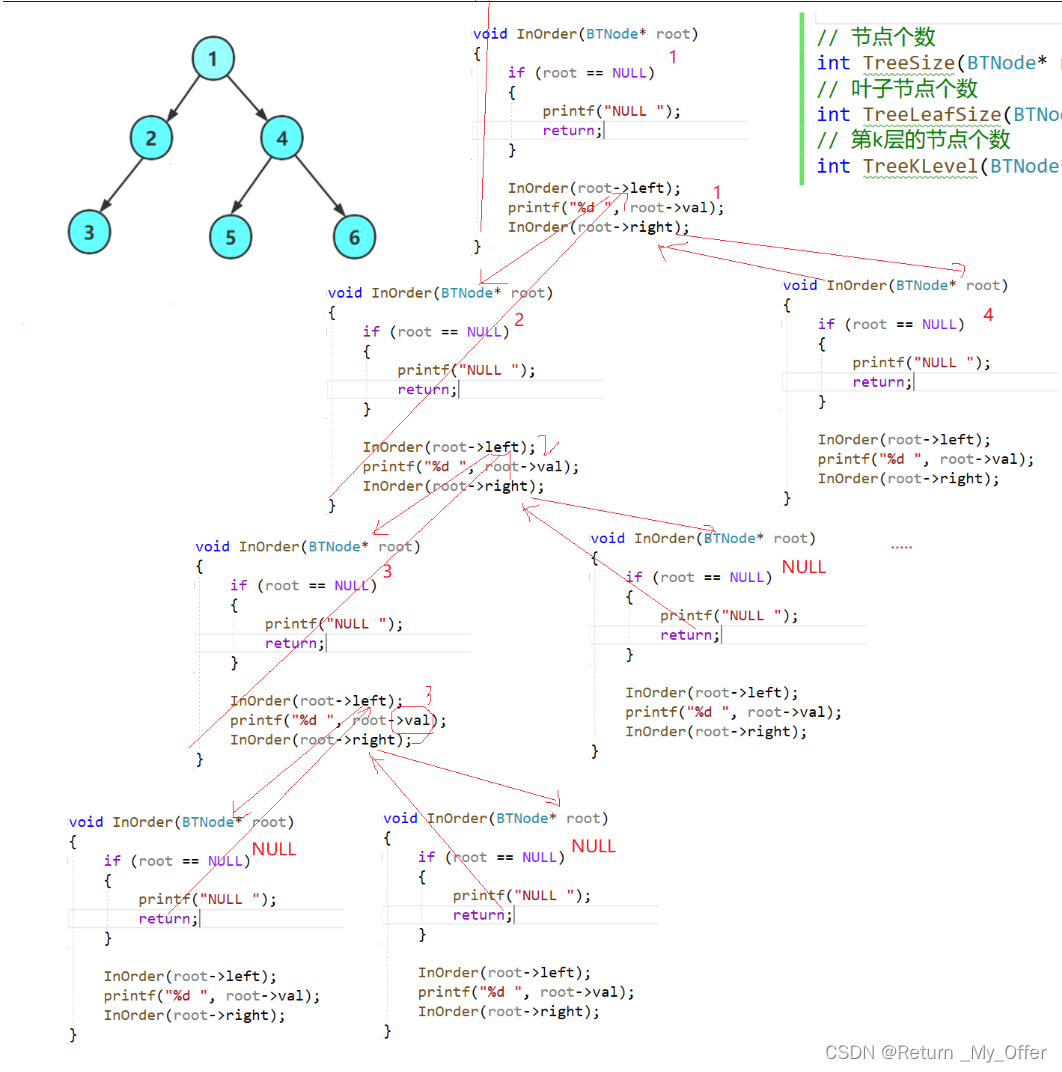
中后序递归展开图大家可以下去自己画图试一试
总的代码实现如下
#include<stdio.h>
#include<stdlib.h>// 不是增删查改,学习二叉树结构
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}void PrevOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}// 节点个数
//int TreeSize(BTNode* root)
//{
// static int size = 0;
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}//int size = 0;
//int TreeSize(BTNode* root)
//{
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}// 叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}// 第k层的节点个数
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1){return 1;}return TreeKLevel(root->left, k - 1)+ TreeKLevel(root->right, k - 1);
}int main()
{// 手动构建BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;PrevOrder(node1);printf("\n");InOrder(node1);printf("\n");PostOrder(node1);printf("\n");printf("%d\n", TreeSize(node1));//size = 0;printf("%d\n", TreeSize(node1));return 0;
}
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;HPDataType _size;HPDataType _capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
bool HeapEmpty(HP* php);
HPDataType HeapTop(HP* php);
#include"Heap.h"
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->_size = 0;php->_capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->_size = 0;php->_capacity = 0;
}void AdJustUP(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);//C语言交换函数可自行尝试解决child = parent;parent = (parent - 1) / 2;}else {break;}}
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->_capacity == php->_size){int NewCapacity = php->_capacity = 0 ? 4 : php->_capacity * 2;HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * NewCapacity);if (temp == NULL) {perror("realloc fail");exit(-1);}php->a = temp;php->_capacity = NewCapacity;}php->a[php->_size] = x;php->_size++;AdJustUP(php->a, php->_size - 1);
}void HeapPop(HP* php)
{assert(php);assert(php->_size > 0);Swap(&php->a[0], &php->a[php->_size - 1]);--php->_size;AdjustDown(php->a, php->_size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->_size > 0);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->_size == 0;
}
相关文章:

【数据结构】:二叉树与堆排序的实现
1.树概念及结构(了解) 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的有一个特殊的结点&#…...

纯css手写switch
CSS 手写switch 纯css手写switchcss变量 纯css手写switch 思路: switch需要的元素有:开关背景、开关按钮。点击按钮后,背景色变化,按钮颜色变化,呈现开关打开状态。 利用typecheckbox,来实现switch效果(修…...

PyTorch 深度学习之处理多维特征的输入Multiple Dimension Input(六)
1.Multiple Dimension Logistic Regression Model 1.1 Mini-Batch (N samples) 8D->1D 8D->2D 8D->6D 1.2 Neural Network 学习能力太好也不行(学习到的是数据集中的噪声),最好的是要泛化能力,超参数尝试 Example, Arti…...

LeetCode【438】找到字符串中所有字母异位词
题目: 注意:下面代码勉强通过,每次都对窗口内字符排序。然后比较字符串。 代码: public List<Integer> findAnagrams(String s, String p) {int start 0, end p.length() - 1;List<Integer> result new ArrayL…...
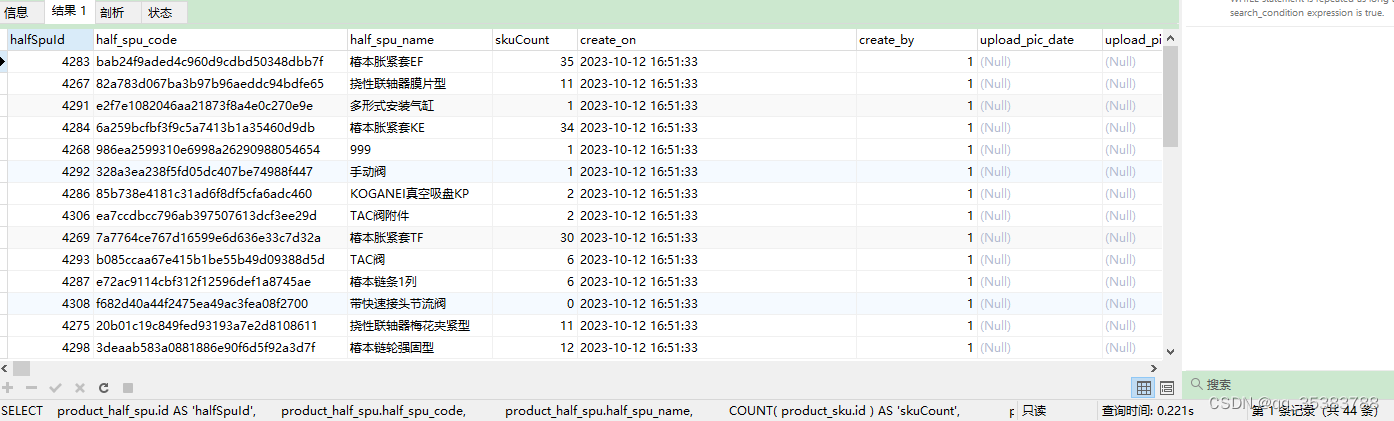
关于LEFT JOIN的一次理解
先看一段例子: SELECTproduct_half_spu.id AS halfSpuId,product_half_spu.half_spu_code,product_half_spu.half_spu_name,COUNT( product_sku.id ) AS skuCount,product_half_spu.create_on,product_half_spu.create_by,product_half_spu.upload_pic_date,produc…...

各报文段格式集合
数据链路层-- MAC帧 前导码8B:数据链路层将封装好的MAC帧交付给物理层进行发送,物理层在发送MAC帧前,还要在前面添加8字节的前导码(分为7字节的前同步码1字节的帧开始定界符)MAC地址长度6B数据长度46~1500B…...

【算法-动态规划】最长公共子序列
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...
区块链游戏的开发流程
链游(Blockchain Games)的开发流程与传统游戏开发有许多相似之处,但它涉及到区块链技术的集成和智能合约的开发。以下是链游的一般开发流程,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司&…...

目标检测网络系列——YOLO V2
文章目录 YOLO9000better,更准batch Normalization高分辨率的训练使用anchor锚框尺寸的选择——聚类锚框集成改进——直接预测bounding box细粒度的特征图——passthrough layer多尺度训练数据集比对实验VOC 2007VOC 2012COCOFaster,更快网络模型——Darknet19训练方法Strong…...
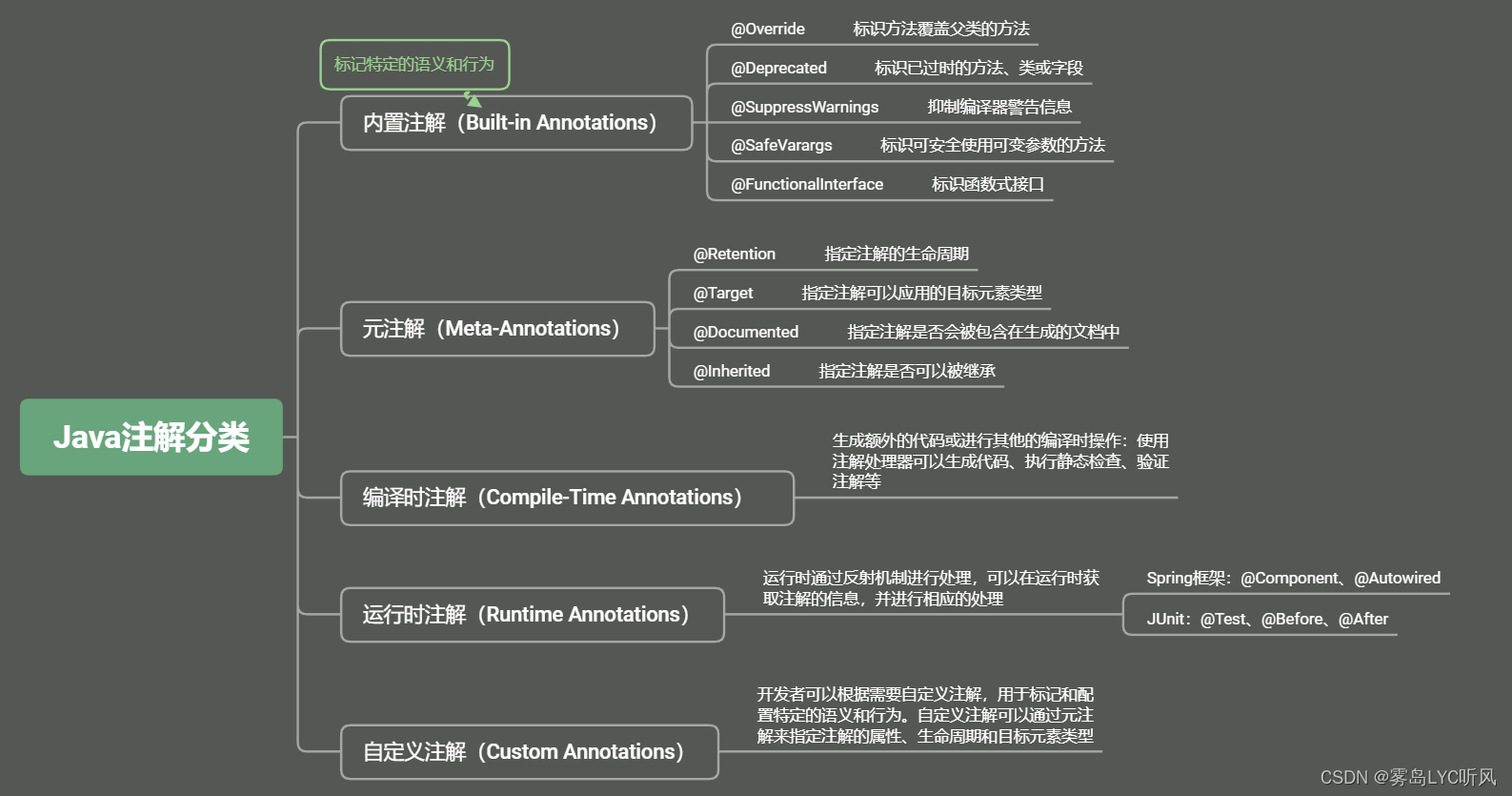
15. Java反射和注解
Java —— 反射和注解 1. 反射2. 注解 1. 反射 动态语言:变量的类型和属性可以在运行时动态确定,而不需要在编译时指定 常见动态语言:Python,JavaScript,Ruby,PHP,Perl;常见静态语言…...
pdf处理工具 Enfocus PitStop Pro 2022 中文 for mac
Enfocus PitStop Pro 2022是一款专业的PDF预检和编辑软件,旨在帮助用户提高生产效率、确保印刷品质量并减少错误。以下是该软件的一些特色功能: PDF预检。PitStop Pro可以自动检测和修复常见的PDF文件问题,如缺失字体、图像分辨率低、颜色空…...
微信小程序入门开发教程
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...

php函数
1. strstr() 返回a在b中的第一个位置 2.substr() 截取字符串 3.PHP字符串函数parse_str(将字符串解析成多个变量)-CSDN博客 4.explode() 字符串分割为数组 5.trim() 1.去除字符串两边的 空白字符 2.去除指定字符 6.extract()函数从数组里…...

3.3 封装性
思维导图: 3.3.1 为什么要封装 ### 3.3.1 为什么要封装 **封装**,在Java的面向对象编程中,是一个核心的思想。它主要是为了保护对象的状态不被外部随意修改,确保数据的完整性和安全性。 #### **核心思想:** - 保护…...

Redis魔法:点燃分布式锁的奇妙实现
分布式锁是一种用于在分布式系统中控制对共享资源的访问的锁。它与传统的单机锁不同,因为它需要在多个节点之间协调以确保互斥访问。 本文将介绍什么是分布式锁,以及使用Redis实现分布式锁的几种方案。 一、前言 了解分布式锁之前,需要先了…...

iOS 项目避坑:多个分类中方法重复实现检测
#前言 在项目中,我们经常会使用分类 -> category。category在实际项目中一般有两个左右:1.给已有class增加方法,扩充起能力、2.将代码打散到多个文件中,避免因为一个类过于复杂而导致代码篇幅过长(应用于viewController中很好用) 但是 category 也有很多弊端~ **首…...
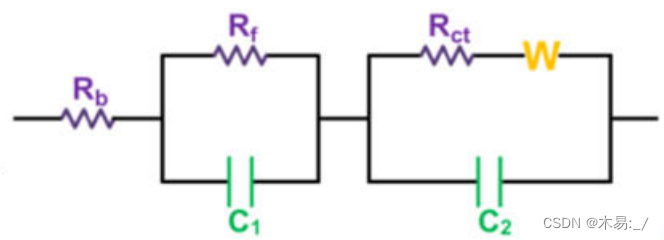
【003】EIS数据分析_#LIB
EIS数据分析 1. EIS测试及数据获取2. EIS数据分析2.1 EIS曲线划分 1. EIS测试及数据获取 点击查看往期介绍 2. EIS数据分析 2.1 EIS曲线划分 一般来说,实轴处的截获表示体电阻(Rb),它反映了电解质,隔膜和电极的电导率。高频区的半圆对应于…...
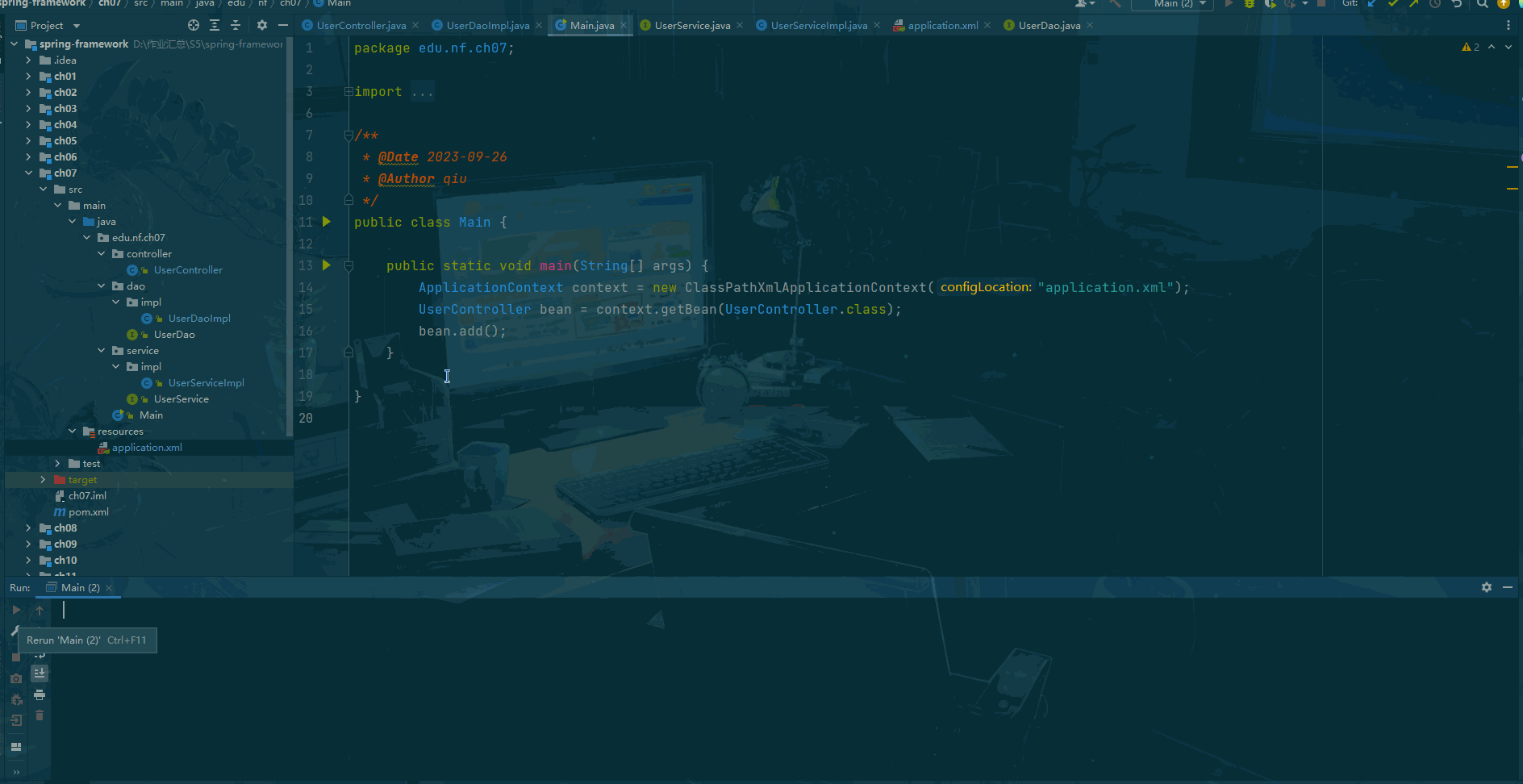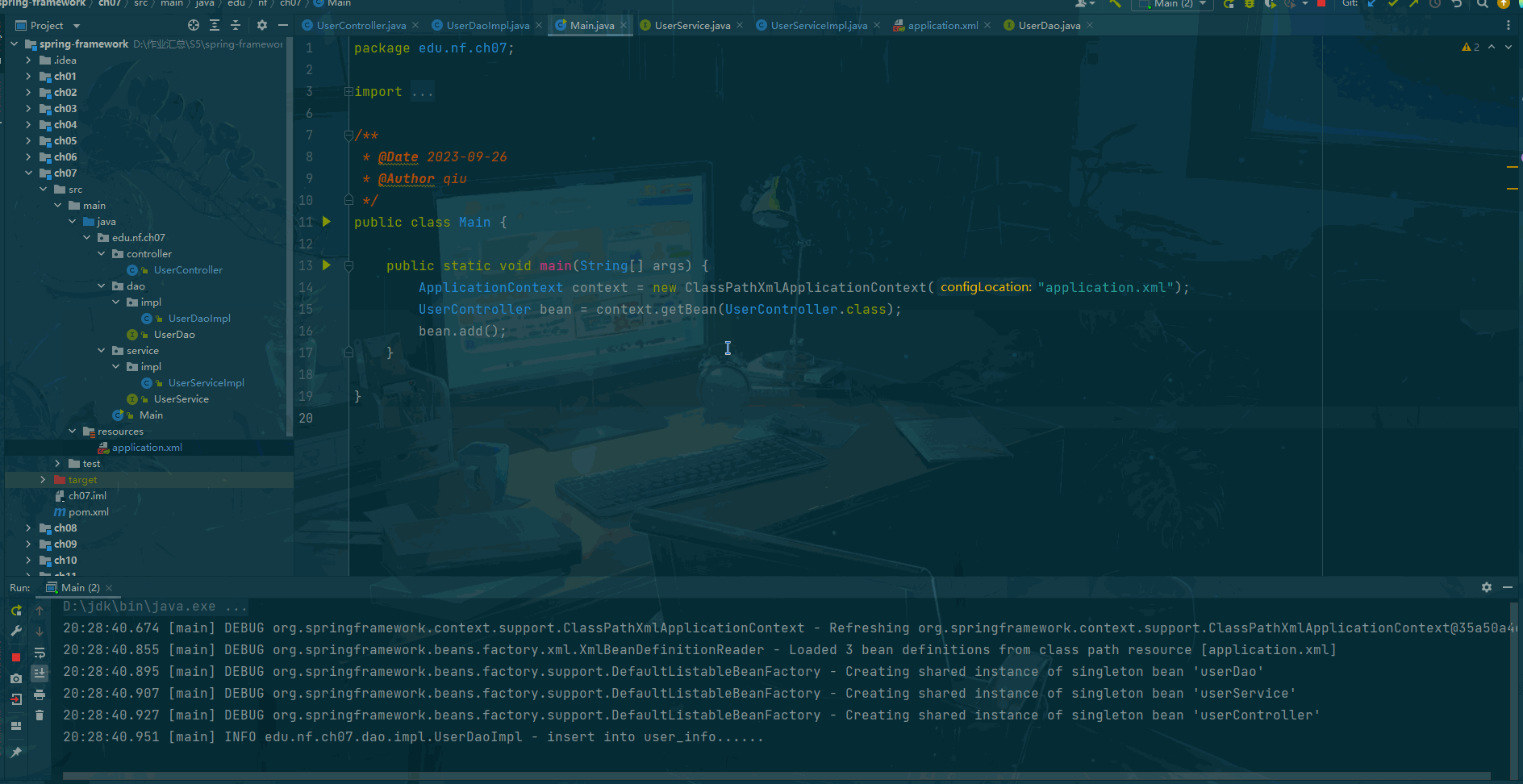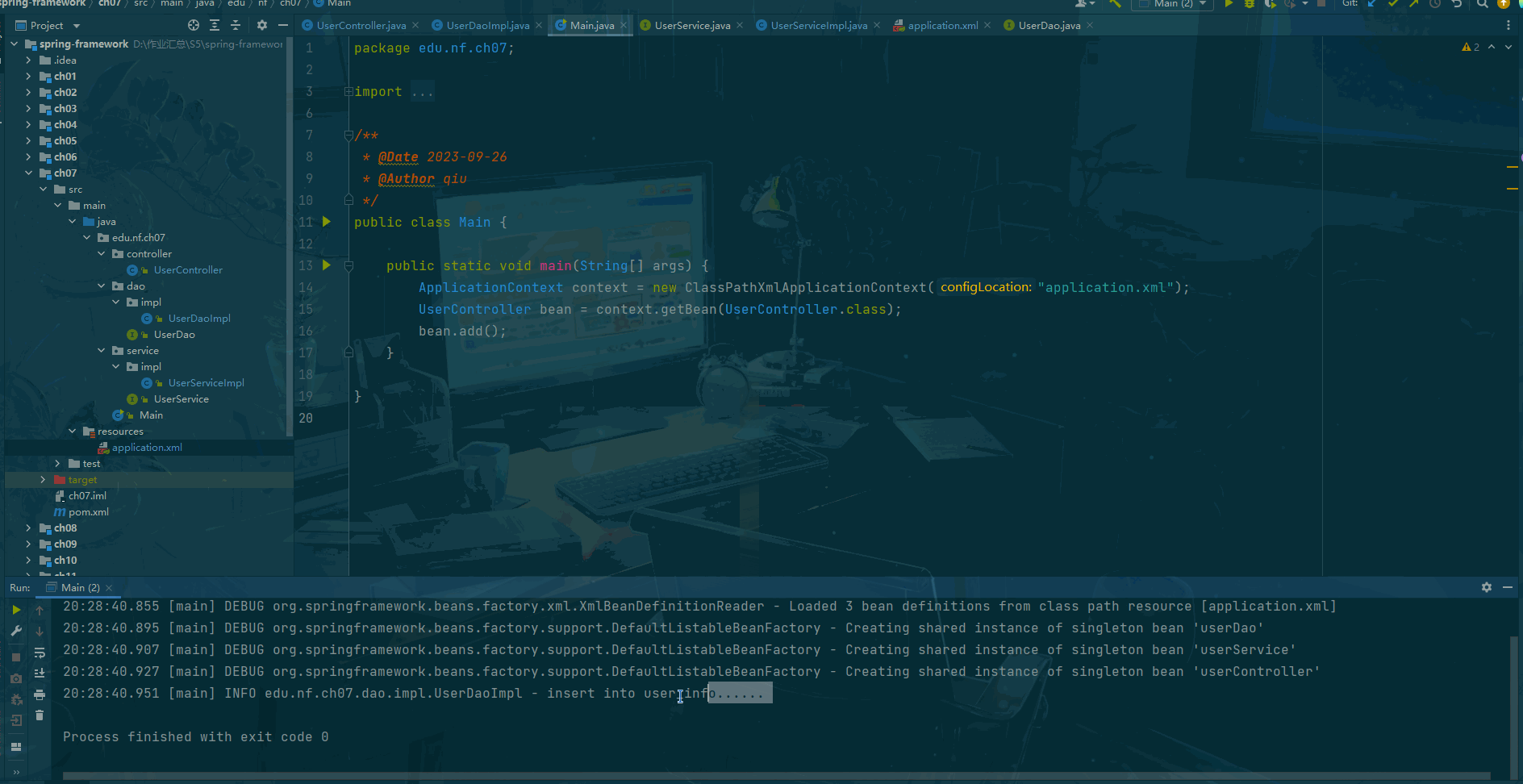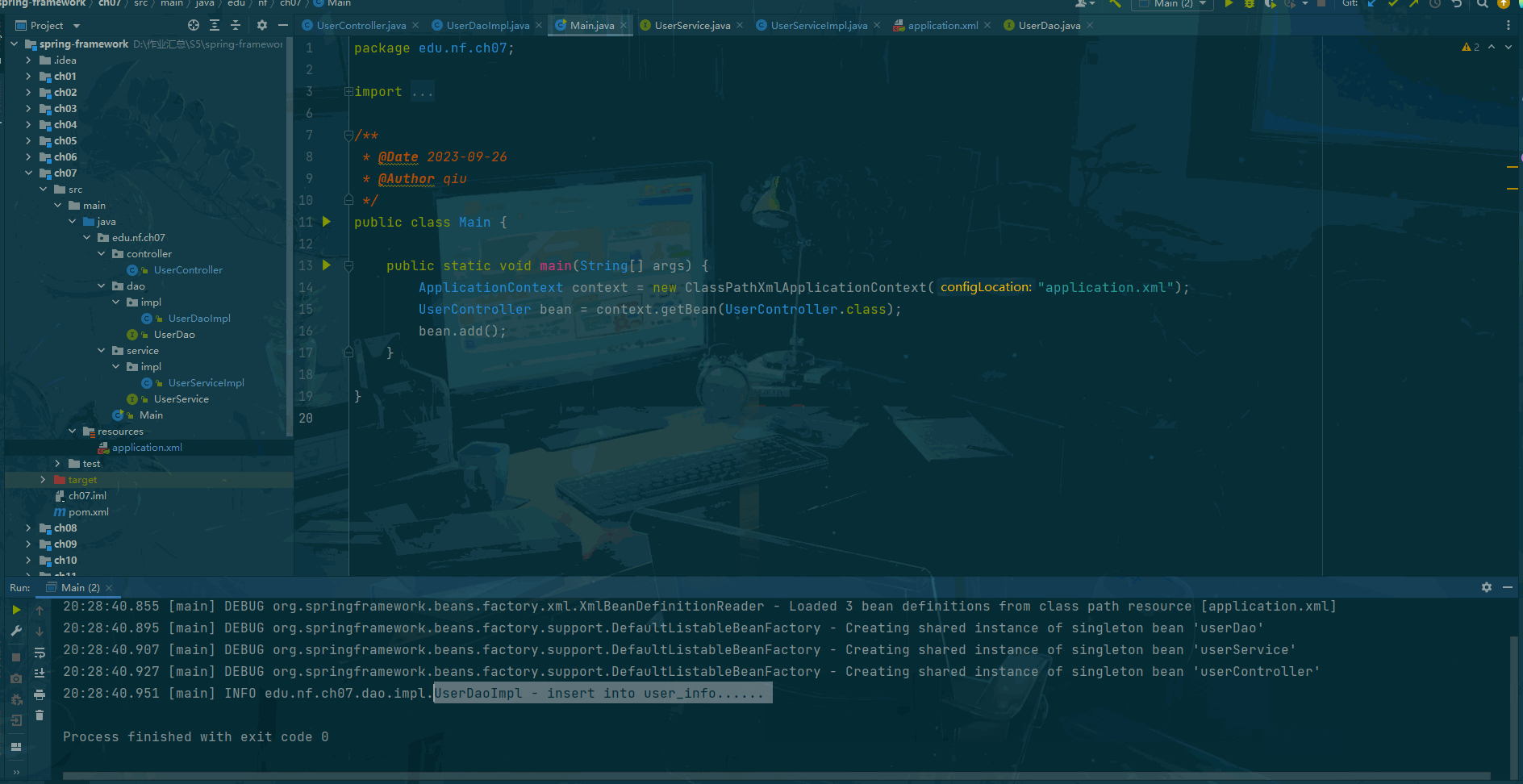
Sprint framework Day07:注解结合 xml 配置
前言 Spring注解结合XML配置是指在Spring应用中,使用注解和XML配置的方式来进行Bean的定义、依赖注入和其他配置。这种方式可以充分利用Spring框架的注解和XML配置两种不同的配置方式的特点。 在Spring框架中,我们可以使用注解来定义Bean,如…...
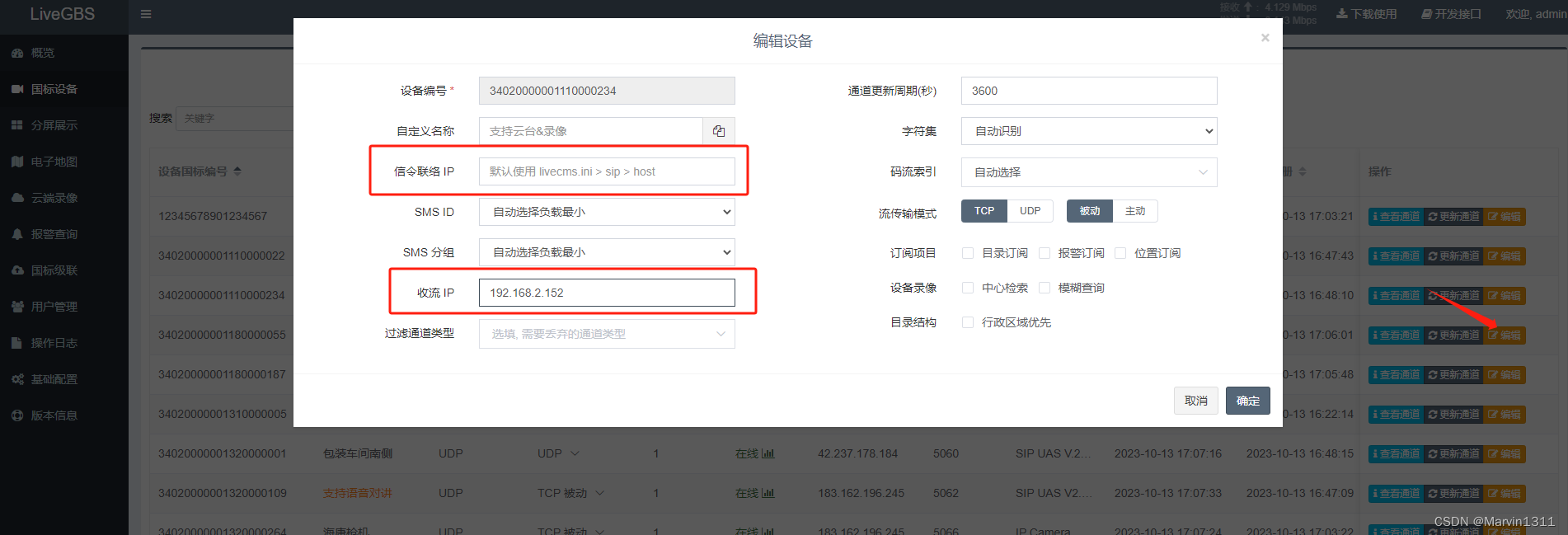
LiveGBS流媒体平台GB/T28181功能-国标流媒体服务同时兼容内网收流外网收流多网段设备收流
LiveGBS流媒体平台GB/T28181功能-国标流媒体服务同时兼容内网收流外网收流多网段设备收流 1、背景2、设备接入播放2.1、查看通道2.2、直播播放 3、默认收流地址配置4、其它网络设备收流配置5、搭建GB28181视频直播平台 1、背景 服务器部署的时候,可能有多个网卡多个…...
)
js题解(四)
文章目录 批量改变对象的属性判断是否包含数字判断是否符合指定格式 批量改变对象的属性 给定一个构造函数 constructor,请完成 alterObjects 方法,将 constructor 的所有实例的 greeting 属性指向给定的 greeting 变量。 function alterObjects(const…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
