高数笔记03:几何、物理应用

图源:文心一言
本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝
- 第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武忠祥
📇目录
📇目录
🦮思维导图
🐳向量代数
🐋数量积【数字】
🐋向量积【向量】
🐋混合积【数字】
🐳空间解析几何
🐋平面空间与直线
🐋曲面与空间曲线
🐳积分学的几何应用
🐋单积分、二重积分
🐋三重积分
🐋曲线积分
🐋曲面积分
🐋多元积分应用
🐳场论初步
🔚结语
🦮思维导图

- 🌸思维导图为整理武老师基础教材所列内容,时间关系有些仓促,请多包涵~
- 🌸博文后面会以大纲的形式复述一遍,面向复习,不会写得很详细,且可能有误;较为重要的内容有从网络找相关配图并给出大佬博文链接~
-
🐳向量代数
-
🐋数量积【数字】
- 几何表示:
- 代数表示:
- 几何应用
- 求夹角
- 判定垂直
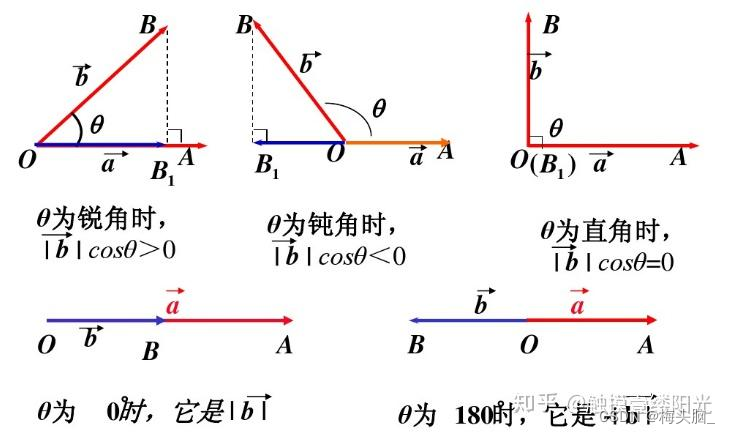
图源:线性代数~数量积 - 知乎
- 几何表示:
-
🐋向量积【向量】
- 几何表示
- 模:
- 方向:右手法则
- 模:
- 代数表示:矩阵【首行基坐标,次行向量a的分量,尾行向量b的分量】

图源:向量外积的坐标形式_向量外积的坐标表示-CSDN博客
- 运算规律:
【模不变,方向相反】
- 几何应用
- 求同时垂直于 a 和 b 的向量
- 判定平行
- 求以a和b为邻边的平行四边形的面积
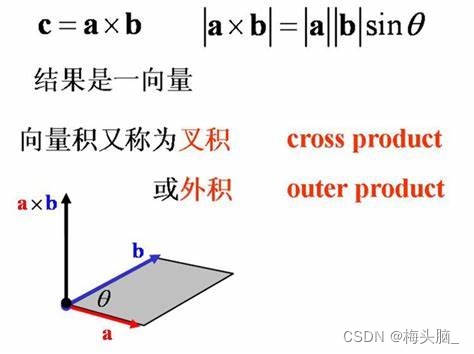
图源:向量的数量积与向量积 - 童趣PBL
- 几何表示
-
🐋混合积【数字】
- 几何表示:
- 代数表示:矩阵【首行向量a的分量,次行向量b的分量,尾行向量c的分量】
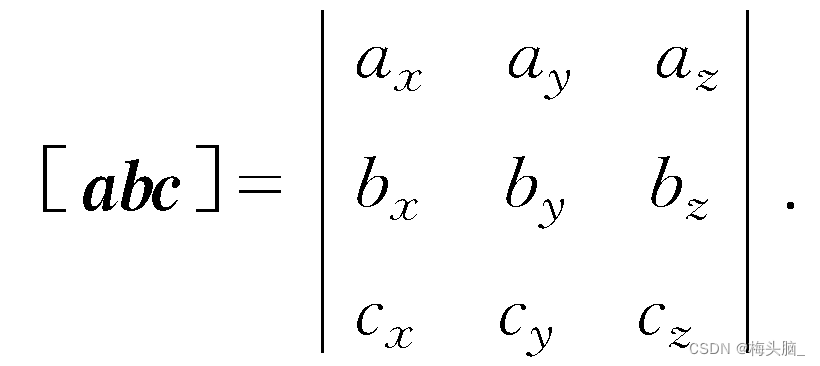
图源:1272. 如何计算混合积?-高等数学-专业词典
- 运算规律
- 轮换对称性:
- 交换变号:
- 原理:矩阵交换1次行列变正负号
- 轮换对称性:
- 几何应用
- 求以a、b、c为邻边的平行六边体的面积
- 求向量共面:(abc)=0【等式中任意两个向量平行,则3个向量必共面】
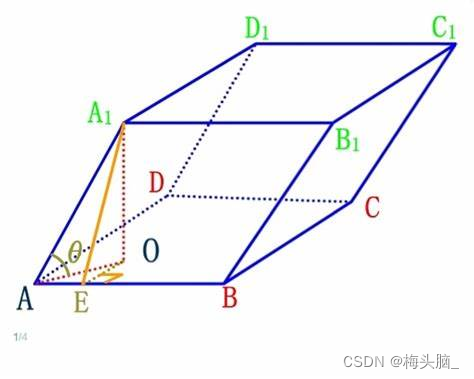
图源:混合积的几何意义
- 几何表示:
-
-
🐳空间解析几何
-
🐋平面空间与直线
- 概要
- 平面方程
- 一般式:
- 点法式:平面上1点(x0,y0,z0)和法线向量(A,B,C)表示直线
- 截距式:经过坐标轴的3个交点表示平面
图源:平面方程_百度百科 (baidu.com)
- 一般式:
- 直线方程
- 一般式:2个平面的交线表示直线
- 对称式:直线上1点(x0,y0,z0)和方向向量(l,m,n)表示直线
- 参数式:直线上1点(x0,y0,z0)和方向向量(l,m,n)表示直线
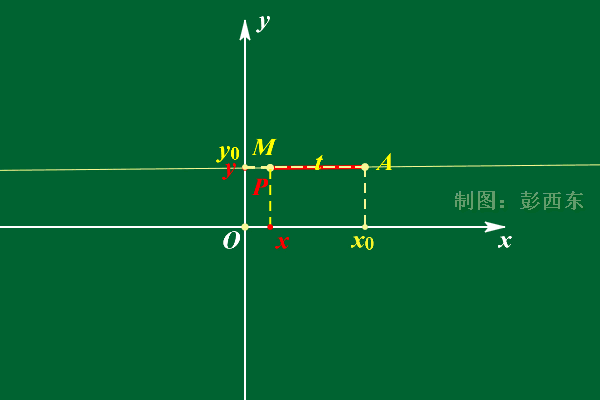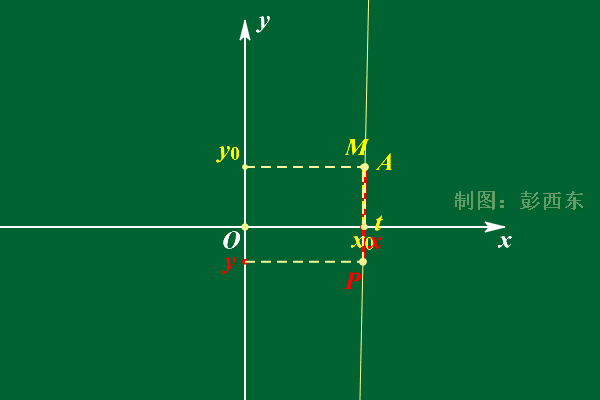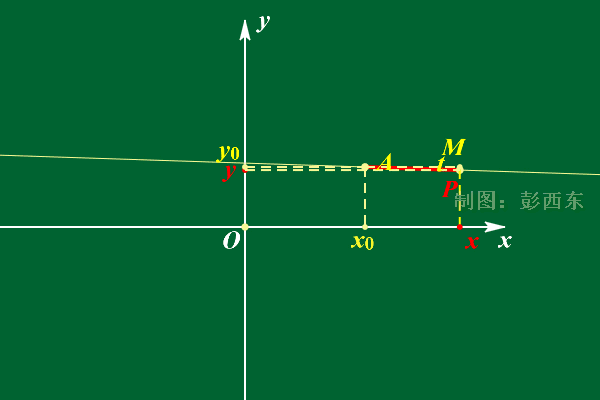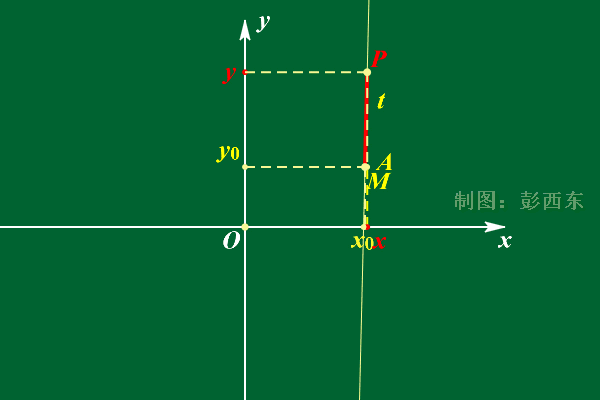
图源:不可不知的——直线的参数方程 (qq.com)
- 一般式:2个平面的交线表示直线
- 点到平面的距离
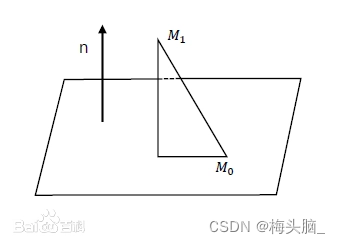
距离为M1M0在平面法向量的投影长度:
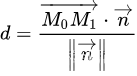
代入点,M1与MO点乘为分子,M0满足平面方程化简,平面法向量的模为分母:
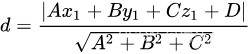
图源:点到平面距离_百度百科 (baidu.com)
- 点到直线的距离
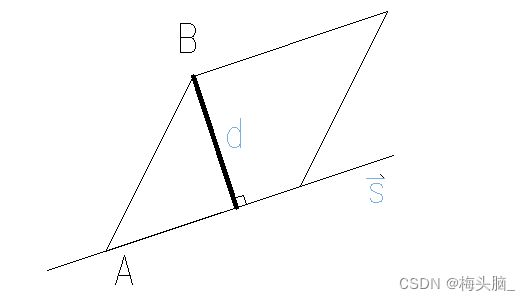
平行四边形满足等式:
代入方向向量S(l,m,n),B(x1,x2,x3),A(x0,y0,z0),得
- 平面方程
- 题型
- 求法向量、切线向量,建立平面与直线的方程
- 求点到直线的距离
- 概要
-
🐋曲面与空间曲线
- 概要
- 曲面方程
-
-
-
- 空间曲线
- 参数式【螺线】

图源:确实没找到...
- 一般式:2个曲面的交线表示空间曲线
- 常见曲面
- 旋转面:平面曲线绕平面直线旋转
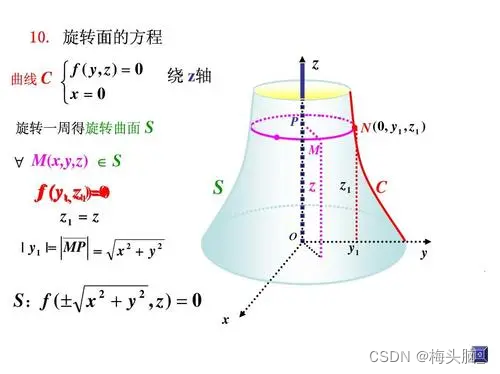
-
柱面:平行与定直线并沿定曲线移动的直线形成的轨迹
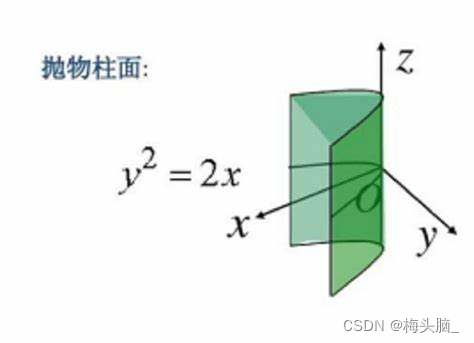
图源:抛物柱面函数 - 快懂百科
- 二次曲面
- 圆柱面
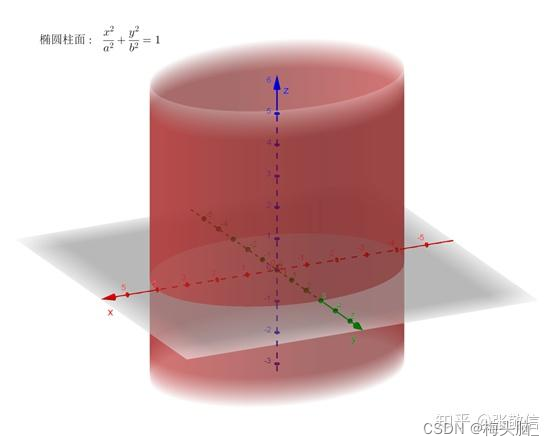
- 圆锥面
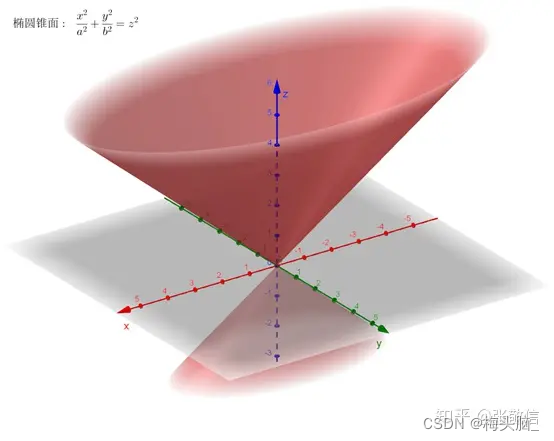
- 旋转抛物面
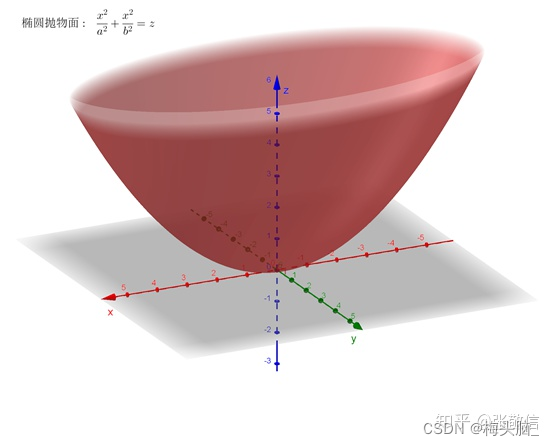
- 椭球面

图源:【高等数学】九种标准二次曲面 - 知乎 (zhihu.com)
- 空间曲线投影
- 投影柱面:曲线一般式联立消去z,得到的二元方程即为母线为z轴的投影柱面
- 投影平面:在投影柱面方程的基础上,增加限制条件 z = 0,检查其它变量的取值范围,即为曲线在xoy面的投影
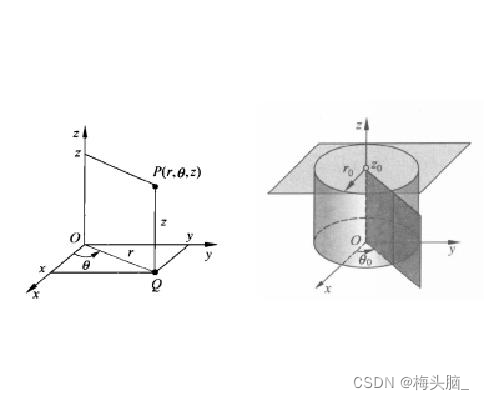
图源:柱面坐标 - 搜狗百科 (sogou.com)
- 旋转面:平面曲线绕平面直线旋转
- 曲面方程
-
题型
- 曲面方程
- 求柱面方程
- 求旋转面方程
- 求投影曲线方程
- 解析几何
- 曲面的切平面与法线,核心:求法向量
- 曲线的切线与法平面,核心:求切向量
- 曲面方程
- 概要
-
-
🐳积分学的几何应用
-
🐋单积分、二重积分
- 概念
- 平面图形的面积
- 直角坐标
- 极坐标
- 直角坐标
- 旋转体体积
- 绕x轴旋转
,其中体积微元
= 底面积
x 高
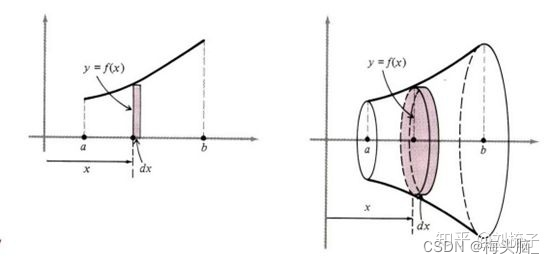
图源:单变量微积分-第十六讲-积分的应用(一) - 知乎
- 绕y轴旋转
,其中体积微元
= 环状窄带周长
x 截面积
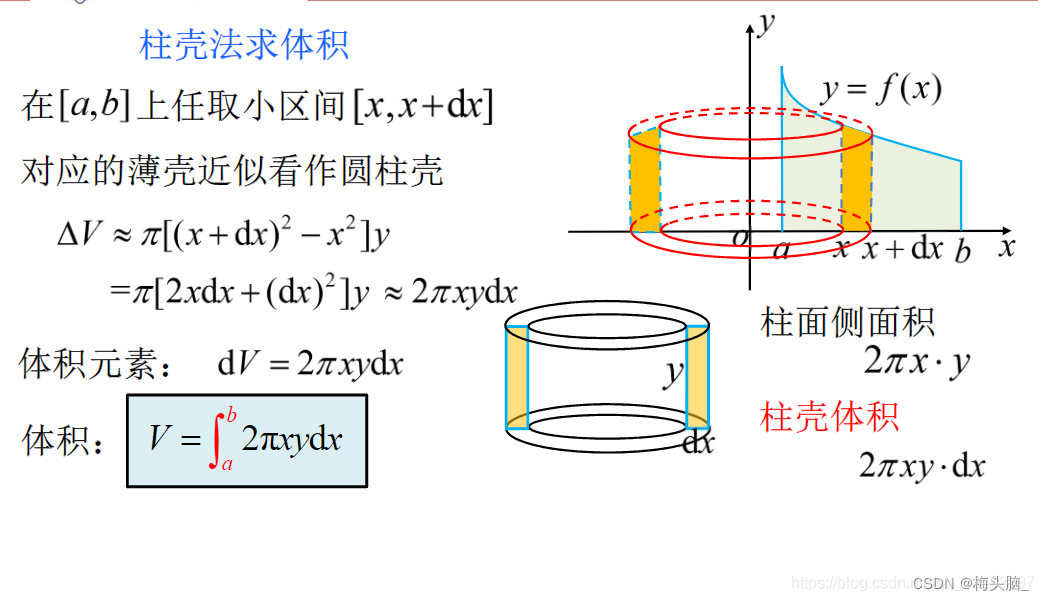
图源:定积分的应用之 柱壳法求旋转体体积_-CSDN博客
- 绕直线旋转
,其中体积微元
= = 环状窄带周长
x 截面积
,
表示点到直线距离
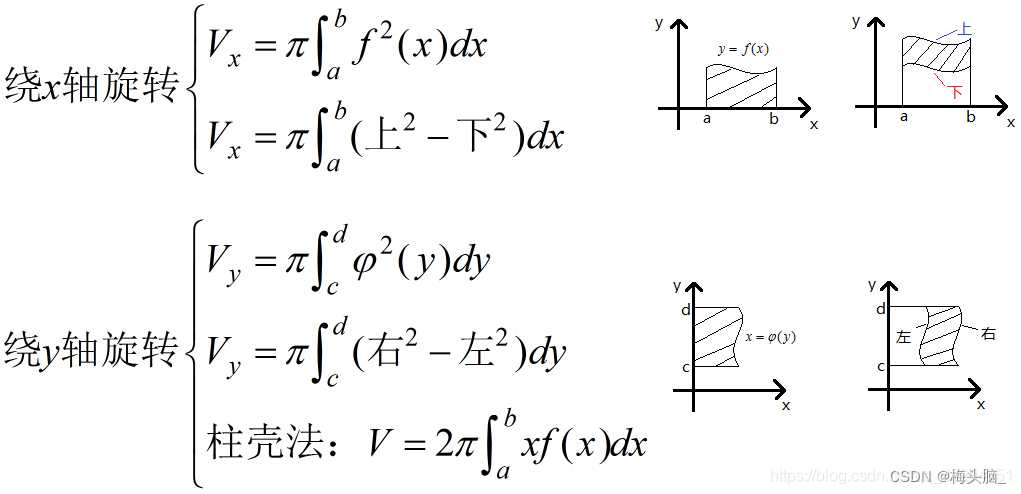
图源:高等数学解题常用公式笔记总结
- 绕x轴旋转
- 曲线弧长:同对弧长的线积分
- 旋转体侧面积
- 绕x轴旋转
,其中面积微元
= 环状窄带周长
x 高度
,

图源:求曲线绕x轴旋转一周的旋转体的侧面积_360问答
- 绕x轴旋转
- 平面图形的面积
- 题型
- 几何应用:
- 定积分求面积
- 绕轴旋转体积
- 物理应用
- 容积 = 底面积 x 高
- 球1底面积
,高度微元
- 球1体积微元
,积分域-1到1/2
- 球1体积
,代入圆的公式
,得
- 球2与球1体积相等,球1体积×2即为所求
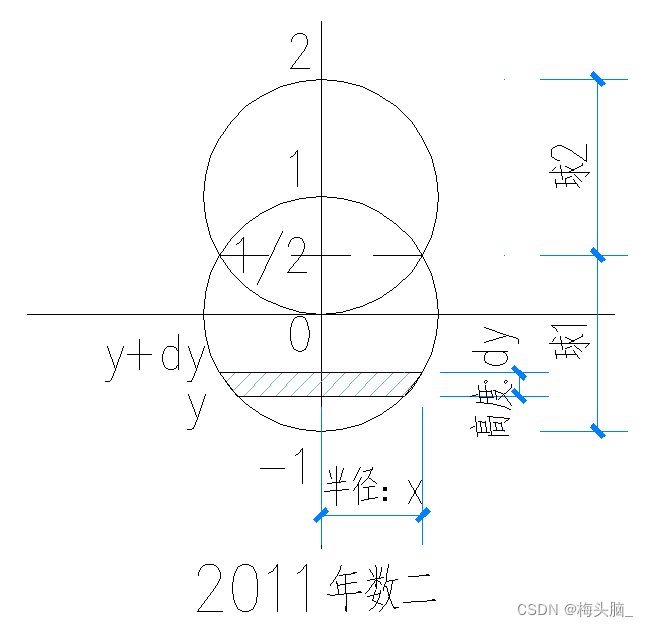
- 球1底面积
- 做功 = 力 x 距离
- 球1受力微元
,距离
;
- 球1做功微元
;
- 以上,球1区域做功
;
- 同理,球2区域做功
;

- 球1受力微元
- 压强 = 压力 x 面积
- 区域1压力:
,区域1面积
;
- 区域1压强微元:
;
- 区域1压强:
;
- 区域2压力:
,区域2面积
;
- 区域2压强微元:
;
- 区域2压强:
;
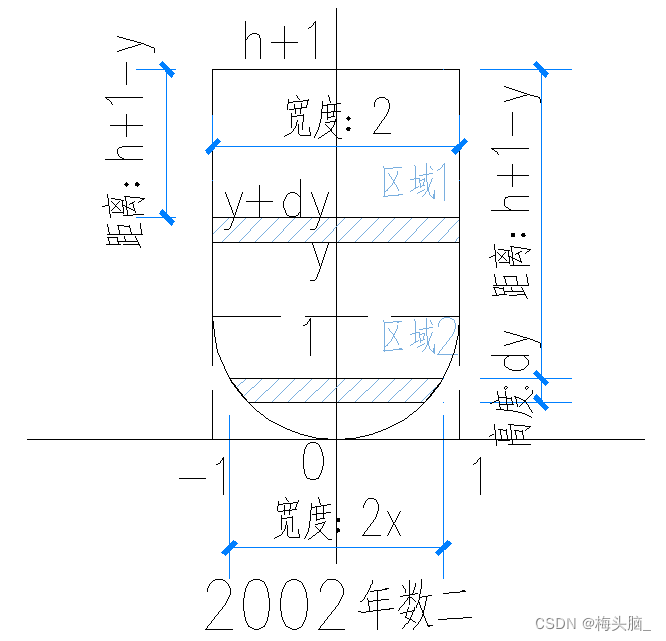
- 区域1压力:
- 容积 = 底面积 x 高
- 几何应用:
- 概念
-
🐋三重积分
- 简述:区域点的函数值 x 体积微元,累加求和
- 性质
- 奇偶性、轮换对称性
- 不等式性质
- 积分中值定理
- 计算
- 先一后二
- 计算
- 作垂直于z轴的直线,穿过封闭底面z1(x,y)与顶面z2(x,y),即z的积分上下限是x,y的函数
- 先计算有关z的积分,再转化为求x,y的二重积分
- 适合坐标
- 印象中比较万能...
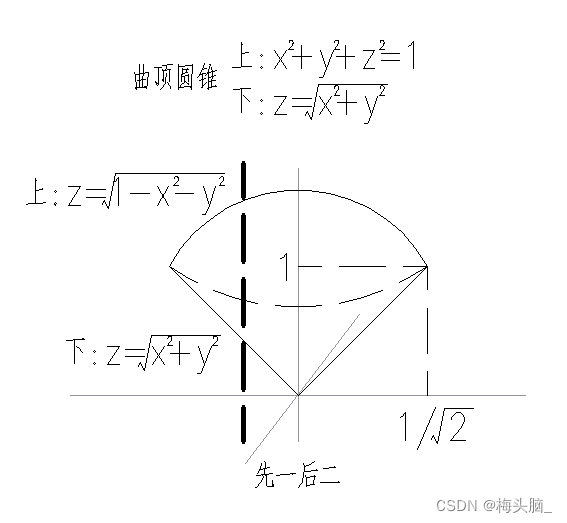
- 计算
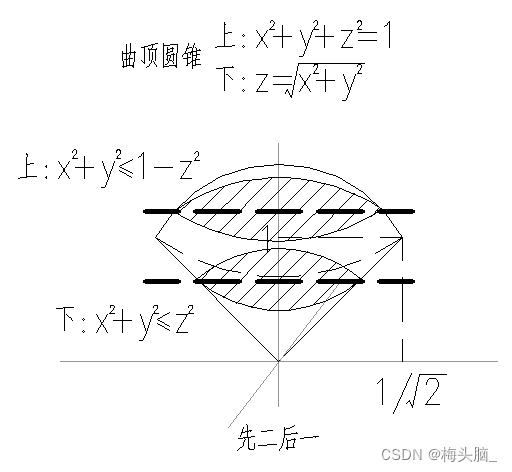
- 先二后一
- 计算
- 作平行于z轴的截面,得到封闭曲线,即z的积分上下限是常数
- 先计算有关x,y的二重积分,再转化为求z的单积分
- 适合坐标
- 被积函数:
,这一步可能需要借助奇偶性、对称性转换得到
- 积分域:
面积较为规则,方便计算
- 被积函数:
- 计算
- 柱坐标
- 与直角坐标的关系
- 坐标
-
-
-
-
- 体积微元
-
-
- 坐标
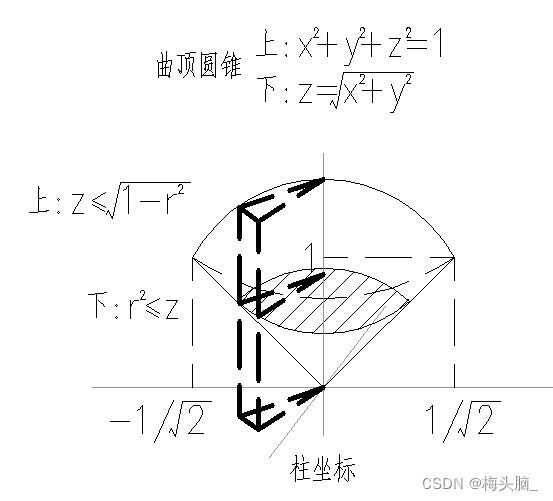
- 适合坐标
- 被积函数:
- 积分域:柱面、锥面
- 被积函数:
- 与直角坐标的关系
- 球坐标
- 与直角坐标的关系
- 坐标
-
-
-
-
- 体积微元
- 坐标
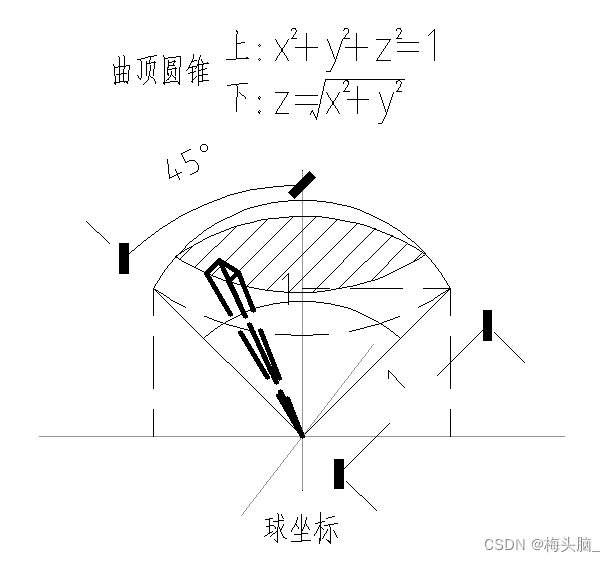
- 适合坐标
- 被积函数:
- 积分域:球面、球壳、锥面
- 被积函数:
- 与直角坐标的关系
- 先一后二
-
🐋曲线积分
- 对弧长的线积分
- 简述:函数值 x 弧长微元,累加求和
- 计算方法
- 直接法
- 体积微元
- 参数方程:
- 直角坐标:
- 极坐标:
- 参数方程:
- 积分域:从小到大【与方向无关,要求结果是正数】
- 体积微元
- 奇偶性【x轴、y轴】
- 对称性【直线y=x】
- 直接法
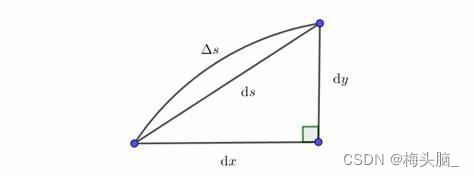
图源:【高等数学】定积分元素法及应用(待续) - 知乎
- 对坐标的线积分
- 简述:函数值 x 有向线段的投影,累加求和
- 计算方法
- 直接法
- 被积函数:代入直角坐标,或极坐标、参数方程
- 积分域:从起点到终点【与方向有关,逆时针为正向】
- 格林公式
- 要求
- 闭区域由分段光滑曲线围成
- 被积函数在积分域上有一节连续偏导数
- 作用:平面坐标的线积分转化为二重积分
- 要求
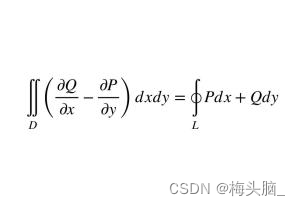
图源:格林公式 - 搜狗百科
- 斯托克斯公式
- 要求
- 闭区域由空间分段光滑曲线围成,方向符合右手法则
- 被积函数在积分域上有一节连续偏导数
- 作用:空间坐标的线积分转化为二重积分
- 要求

图源:斯托克斯公式的意义? - 知乎
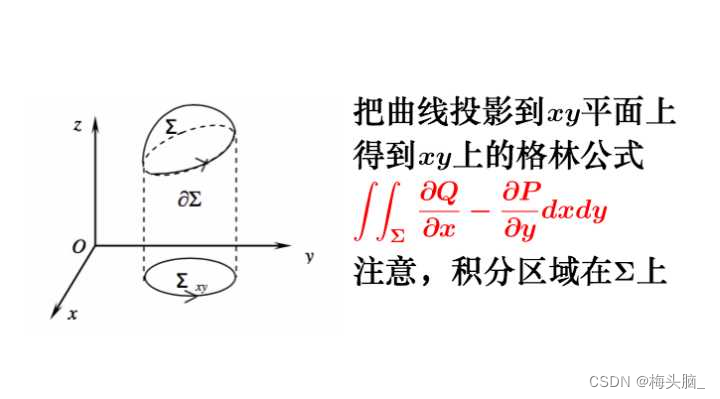
图源:怎么记住斯托克斯公式(Stokes' theorem)? - 知乎
- 直接法
- 方法选择
- 曲线L是否封闭?
- 是:格林【平面】/ 斯托克斯【空间】
- 否:是否与路径无关?
- 是
- 改换路径【一般选择平行坐标轴】
- 寻找原函数【偏积分、凑微分】
- 否
- 直接法【注意方向】
- 补线使用公式
- 是
- 曲线L是否封闭?
- 两类线积分的关系
- 对弧长的线积分 x 曲线在切线方向的余弦 = 对坐标的线积分

图源:多元微积分—— 知乎
- 对弧长的线积分
-
🐋曲面积分
- 对面积的面积分
- 简述:函数值 x 面积微元,累加求和
- 计算方法
- 直接法
- 体积微元:
- 积分域:从小到大【与方向无关,要求结果是正数】
- 体积微元:
- 奇偶性【x轴、y轴】
- 轮换对称性
- 直接法
- 对坐标的面积分
- 简述:函数值 x 有向投影域面积,累加求和
- 计算方法
- 直接法
- 被积函数:代入直角坐标
,或极坐标、参数方程
- 积分域:从起点到终点【与方向有关,上、前、右侧为正向】
- 被积函数:代入直角坐标
- 高斯公式
- 要求
- 闭区域由分段光滑曲线围成
- 被积函数在积分域上有一节连续偏导数
- 作用:空间坐标的面积分转化为三重积分
- 要求
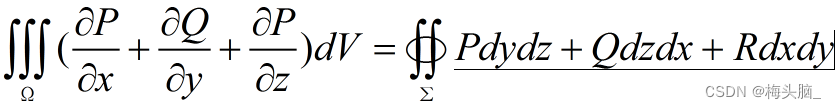
图源:高斯公式 - Bing
- 直接法
- 方法选择
- 曲面是否封闭且不存在奇点?
- 是:高斯公式
- 否
- 直接法【注意方向】
- 补面【不封闭】或作辅助面【存在奇点】使用公式
- 曲面是否封闭且不存在奇点?
- 两类面积分的关系
- 对面积的面积分 x 曲面在切线方向的余弦 = 对坐标的面积分
- 对面积的面积分
-
🐋多元积分应用
- 概要
- 平板面【二重积分】
- 面积
- 被积函数:1
- 质量
- 被积函数:
- 被积函数:
- 质心
- 被积函数:
- 被积函数:
- 转动惯量
- 被积函数:
【对y轴】
- 被积函数:
- 面积
- 推广
- 空间体【三重积分】
- 曲线【一型线积分】
- 曲面【一型面积分】
- 变力做功【二型线积分】
- 通量【二型面积分】
- 平板面【二重积分】
- 题型
- 形心
- 质心
- 变力做功
- 概要
-
-
🐳场论初步
- 方向导数:函数在某点对指定方向求导的结果
- 梯度:函数在这点方向导数最大的方向
- 散度:向量场在某点吸收或散发通量的大小
- 旋度:向量场对某点微元造成的旋转程度
详见大佬博文【我实在是打不动公式了...🫠】微积分-13.场论初步 - 知乎 (zhihu.com)
🔚结语
😶🌫️博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容~
🌟博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,博主肝文的动力++~
🌸博主可能会佛系更新思维导图,在这里:
高等数学_梅头脑_的博客-CSDN博客![]() https://blog.csdn.net/weixin_42789937/category_12380893.html
https://blog.csdn.net/weixin_42789937/category_12380893.html
相关文章:
高数笔记03:几何、物理应用
图源:文心一言 本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝 第1版:查资料、画导图~🧩🧩 参考资料:《高等数学 基础篇》武…...
js + selenium 获取chatgpt的accessToken
chatgpt的accessToken非常有用,在做web api对接时,因为登录超时 会刷新accessToken let elements document.querySelectorAll(.token-string);let concatenatedText [8,9,10].map(index > {return elements[index] ? elements[index].textContent …...

Spring MVC 十一:中文乱码
SpringMVC的中文乱码问题其实已经不是什么问题了,无非就是配置编码方式->解决问题。 但是由于SpringMVC可以通过:xml方式配置、Servlet3.0方式配置,以及是否使用EnableWebMvc等,不同配置方式下,解决中文乱码问题的…...
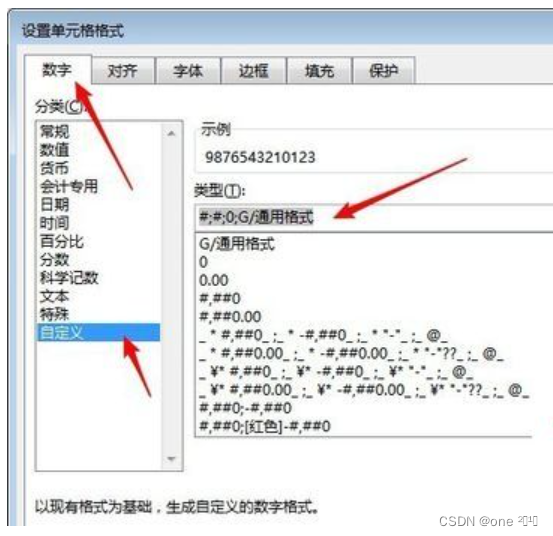
Excel恢复科学技术法显示的数据
Excel中输入位数较大的数据时,软件会自动使用科学计数法显示。很多时候并不需要这样的计数格式,所以需要把它转变为普通的数字格式 操作方法 选中单元格/列/行》右键》设置单元格式 在打开的窗口中,切换到“数字”选项卡,点击“自…...
springboot 志同道合交友网站演示
springboot 志同道合交友网站演示 liu1113625581...
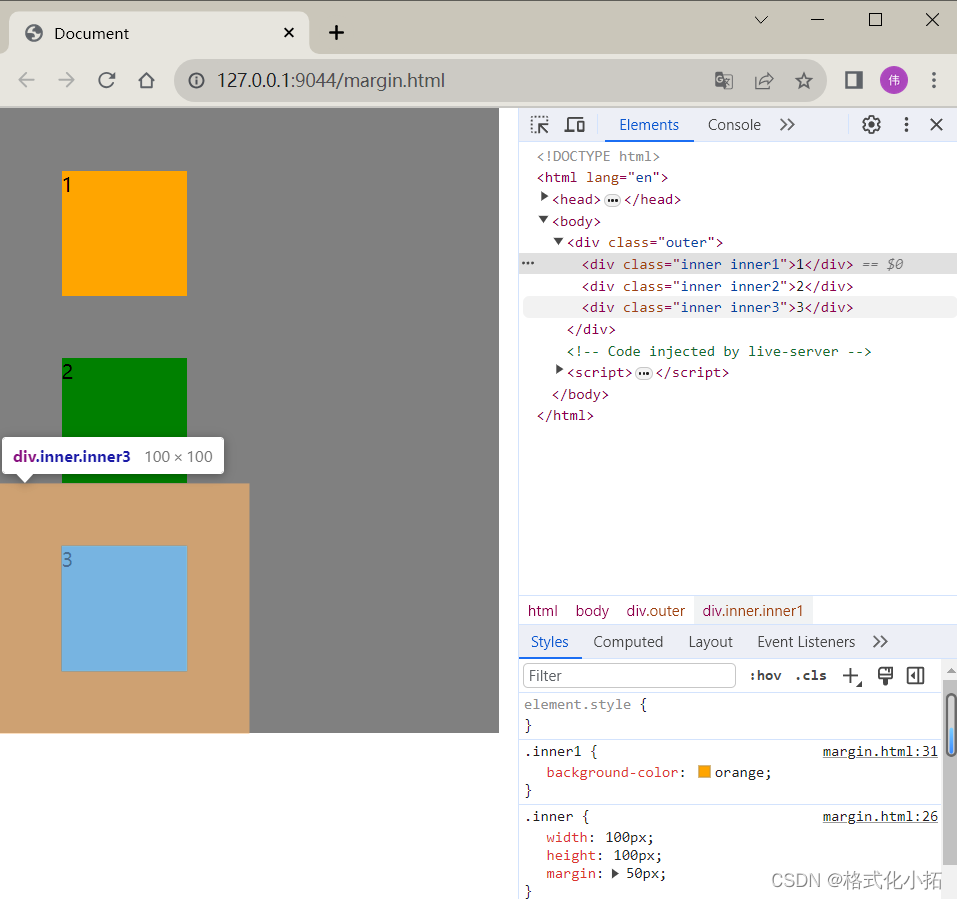
如何理解BFC、开启BFC、BFC解决哪些问题
1.BFC 概念 BFC 英文名为 Block Formatting Context (块级格式化上下文) 具体可查看 MDN 2.BFC的作用 元素开启BFC后,子元素不会发生margin塌陷问题元素开启BFC后,子元素浮动,元素不发生高度塌陷元素开启BFC后,该元素不被其他元…...
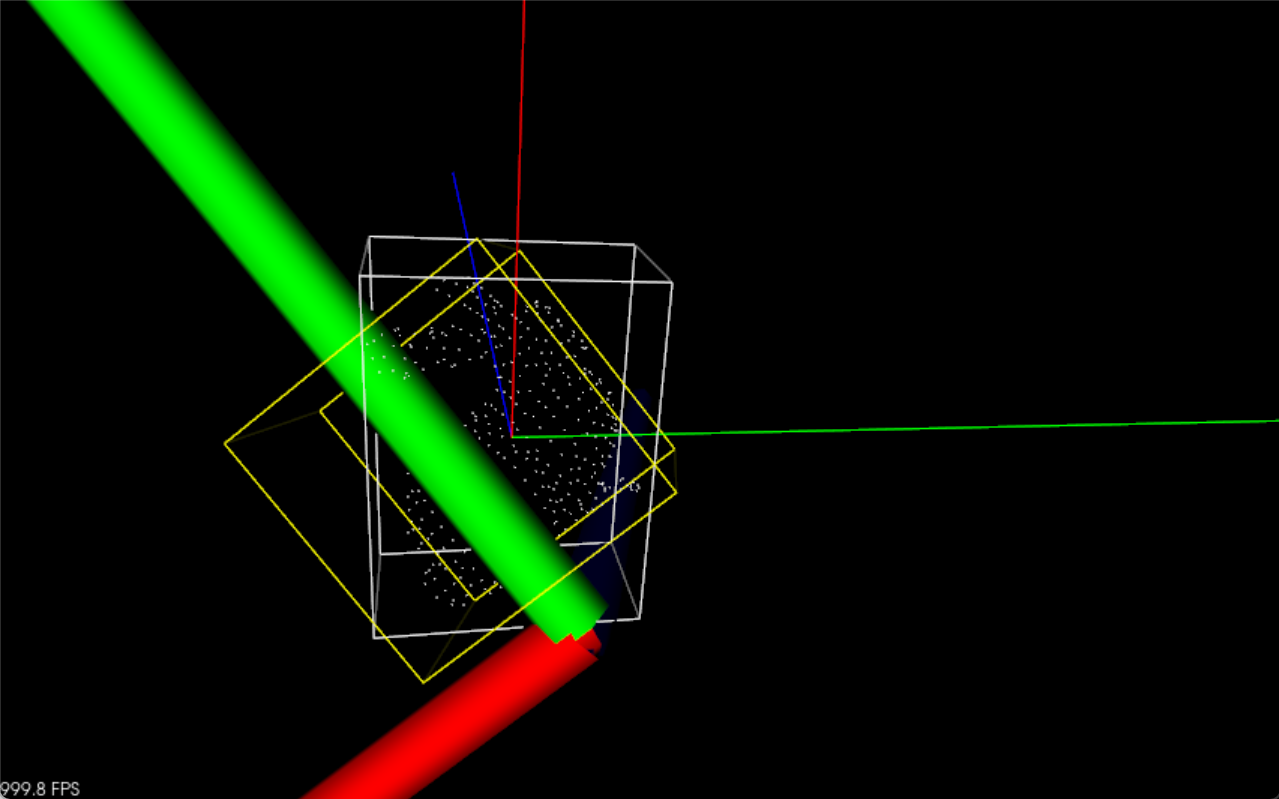
3D包容盒子
原理简述 包围体(包容盒)是一个简单的几何空间,里面包含着复杂形状的物体。为物体添加包围体的目的是快速的进行碰撞检测或者进行精确的碰撞检测之前进行过滤(即当包围体碰撞,才进行精确碰撞检测和处理)。包…...

用 Three.js 创建一个酷炫且真实的地球
接下来我会分步骤讲解,在线示例在数字孪生平台。 先添加一个球体 我们用threejs中的SphereGeometry来创建球体,给他贴一张地球纹理。 let earthGeo new THREE.SphereGeometry(10, 64, 64) let earthMat new THREE.MeshStandardMaterial({map: albed…...
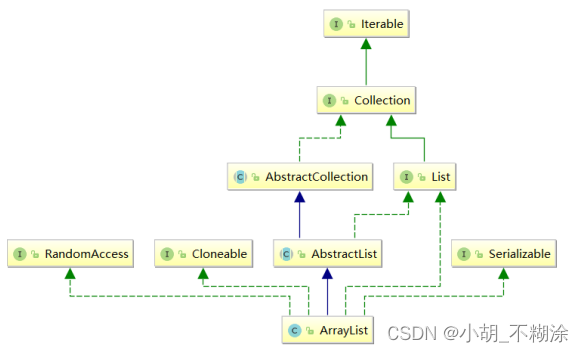
【数据结构】线性表与顺序表
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 线性表与顺序表 1. 线性表2. 顺序表2.1 …...
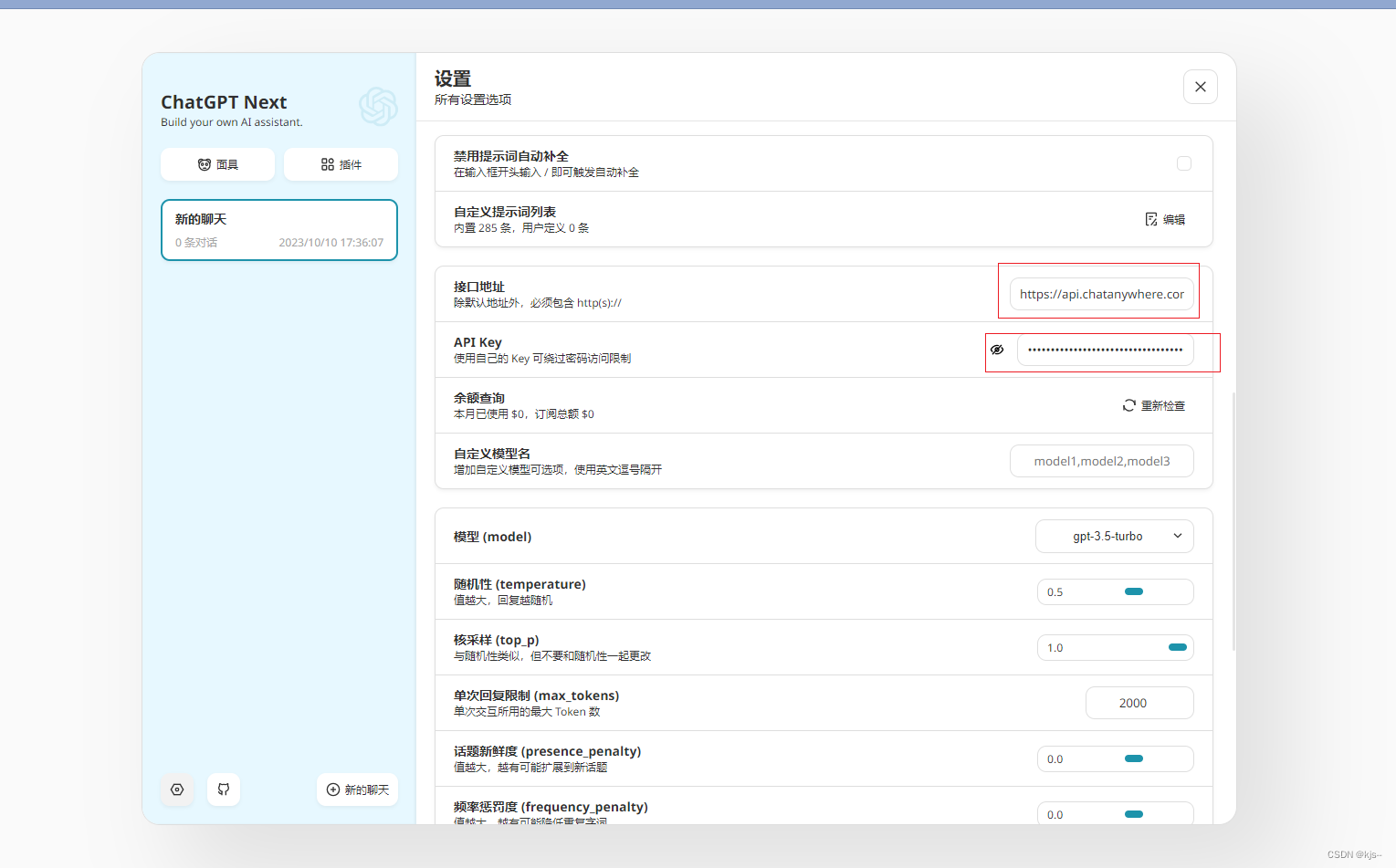
ChatGPT
chatgpt使用地址 https://mycaht.top/#/chat 申请内测免费key https://github.com/chatanywhere/GPT_API_free 设置 接口地址设置改成 https://api.chatanywhere.com.cnAPI Key设置成申请出来的免费key 开始聊天...
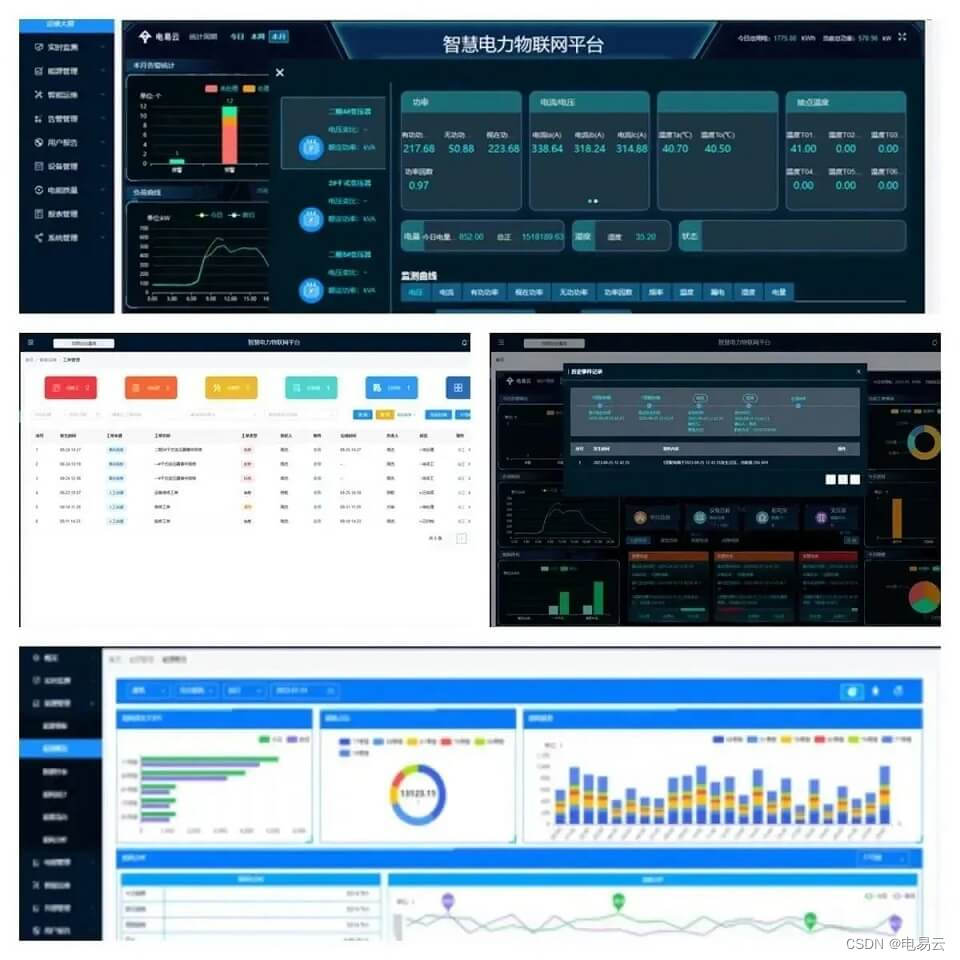
矿区井下智慧用电安全监测解决方案
一、背景 矿区井下作业具有复杂的环境和较高的危险性,对于用电安全的要求尤为严格。传统的管理模式和监测方法往往无法实时、准确地掌握井下用电情况,对安全隐患的排查与预防存在一定局限性。因此,引入智慧用电安全监测解决方案ÿ…...
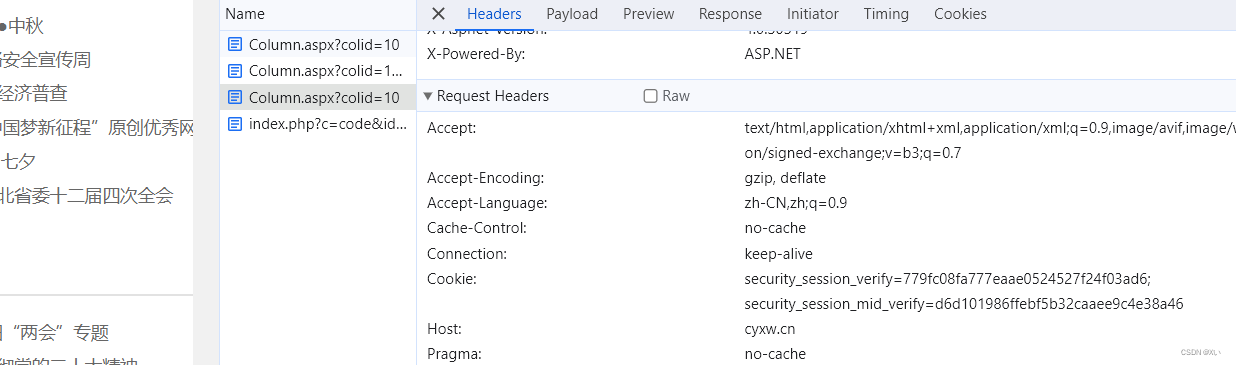
网站列表页加密:三次请求后返回内容多\r
一、抓包第一次请求 url aHR0cDovL2N5eHcuY24vQ29sdW1uLmFzcHg/Y29saWQ9MTA抓包,需要清理浏览器cookie,或者无痕模式打开网址,否则返回的包不全,依照下图中的第一个包进行requests请求 第一次请求后返回 <!DOCTYPE html>…...
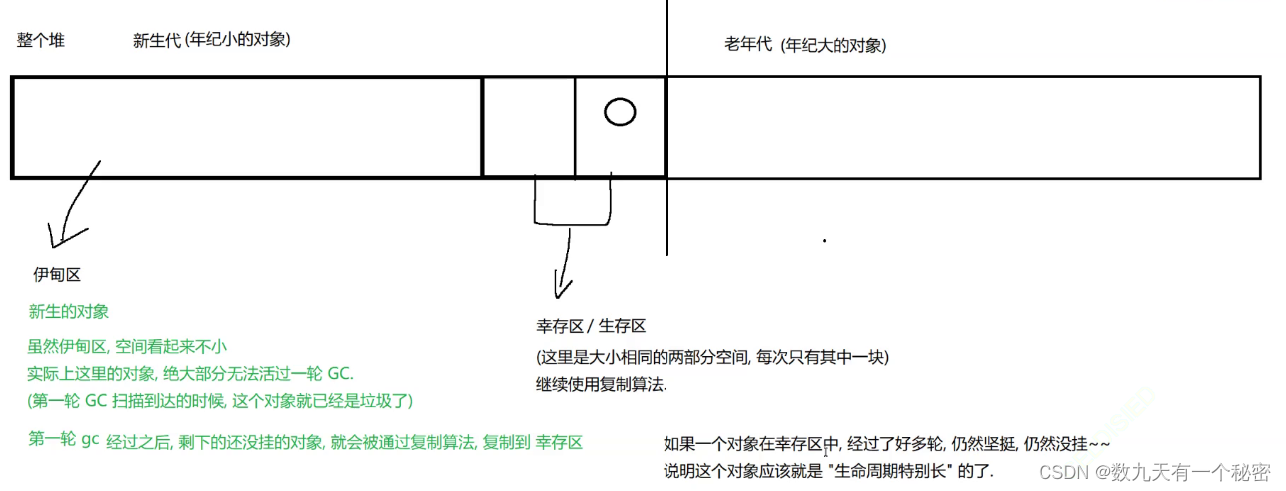
12.JVM
一.JVM类加载机制:把类从硬盘文件加载到内存中 1.java文件,编写时是一个.java文件,编译后现成一个.class的字节码文件,运行的时候,JVM就会读取.class文件,放到内存中,并且构造类对象. 2.类加载流程: a.加载:找到.class文件,打开文件,读取内容,尝试解析文件内容. b.验证:检查…...
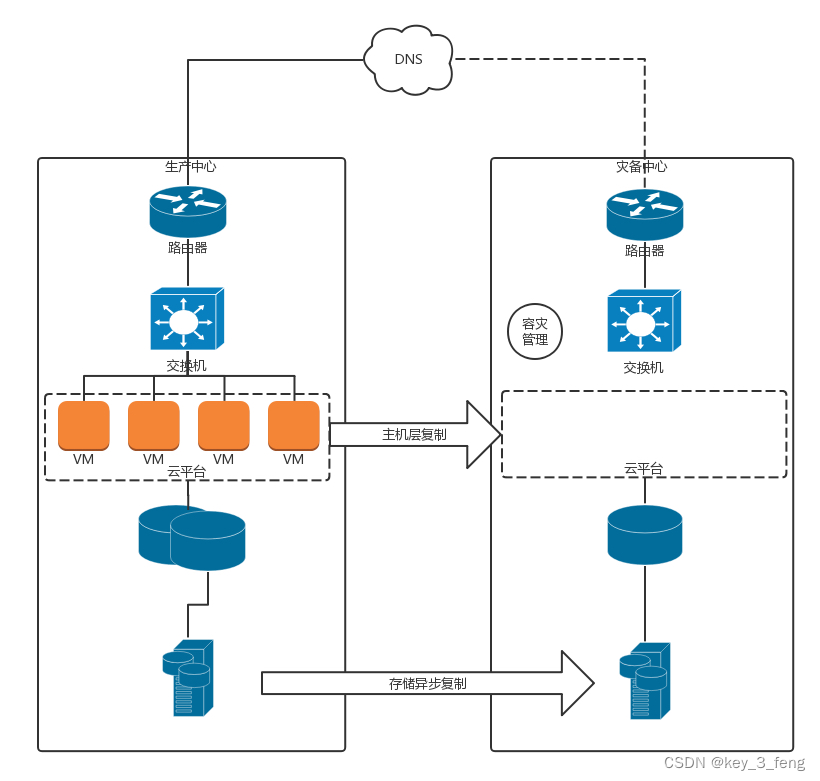
关于网络协议的若干问题(四)
1、QUIC 是一个精巧的协议,它有哪些特性? 答:QUIC 还有其他特性,一个是快速建立连接。另一个是拥塞控制,QUIC 协议当前默认使用了 TCP 协议的 CUBIC(拥塞控制算法)。 CUBIC 进行了不同的设计&…...
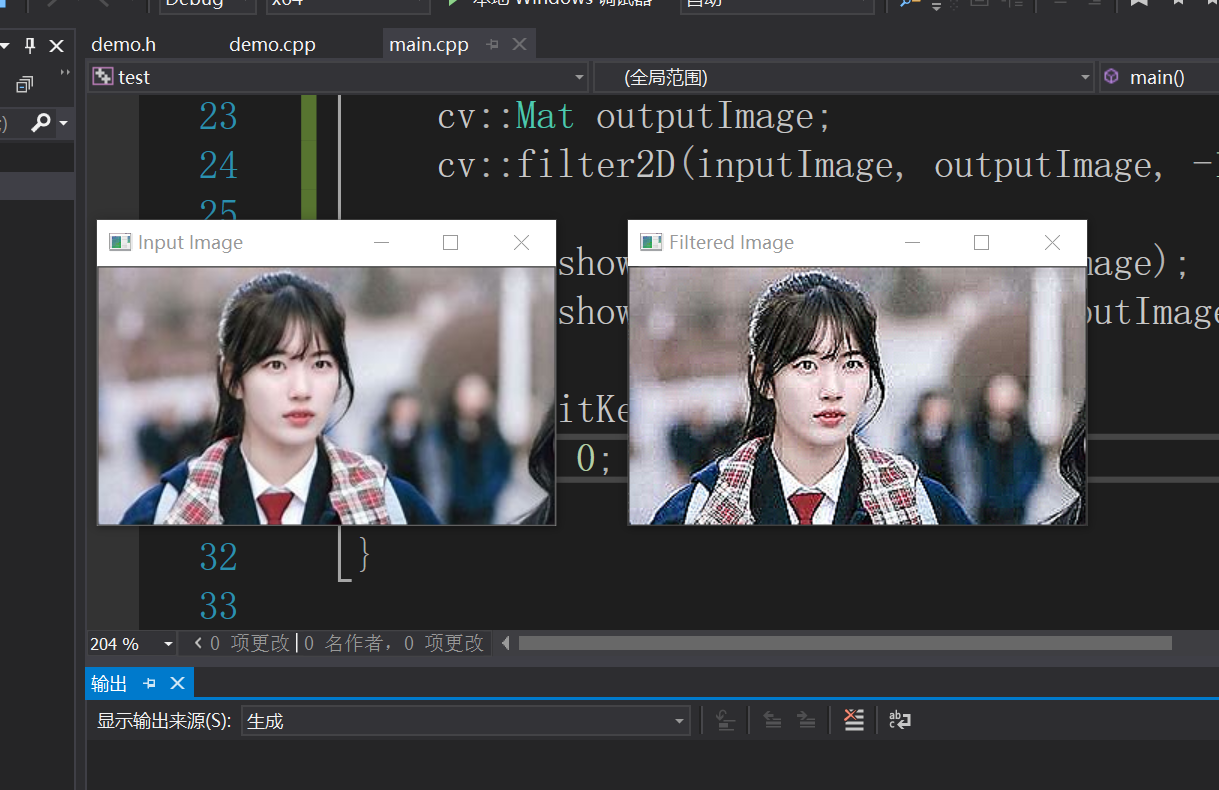
opencv图像卷积操作和常用的图像滤波函数
文章目录 opencv图像卷积操作原理,opencv中常用的图像滤波函数一、图像卷积操作原理:1、卷积操作原理图: 二、opencv常用的图像滤波函数:这些函数的主要作用是对图像进行平滑处理或去除噪声(核心目的是减少图像中的噪声࿰…...
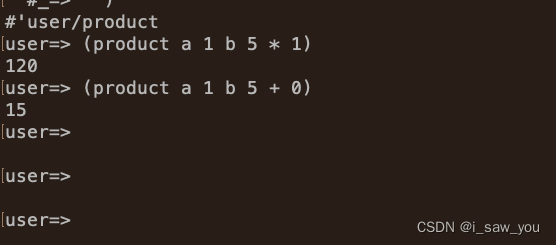
习题1. 31
话不多说 先上代码 (defn product [ term a nxt b](defn iter [a result](if (> a b)1 (* (term a) (iter (nxt a) result))))(iter a 1)) 跟习题1.30比较起来,就是两个地方不同 乘法不能乘0 必须是1。难度来讲,跟1.30难度是一样的。增加了迭代过…...

见微知著:从企业售后技术支持看云计算发展
作者:余凯 售后业务中的细微变化 作为阿里云企业容器技术支持的一员,每天会面对全球各地企业级客户提出的关于容器的各种问题,通过这几年的技术支持的经历,逐步发现容器问题客户的一些惯性,哪些是重度用户࿰…...

C++笔记之如何给 `const char*` 类型变量赋值
C笔记之如何给 const char* 类型变量赋值 code review! 文章目录 C笔记之如何给 const char* 类型变量赋值1.在C中,如果你要给一个 const char* 变量赋值,你通常有几种方法来做这件事,具体取决于你的需求。下面是一些常见的方法:…...
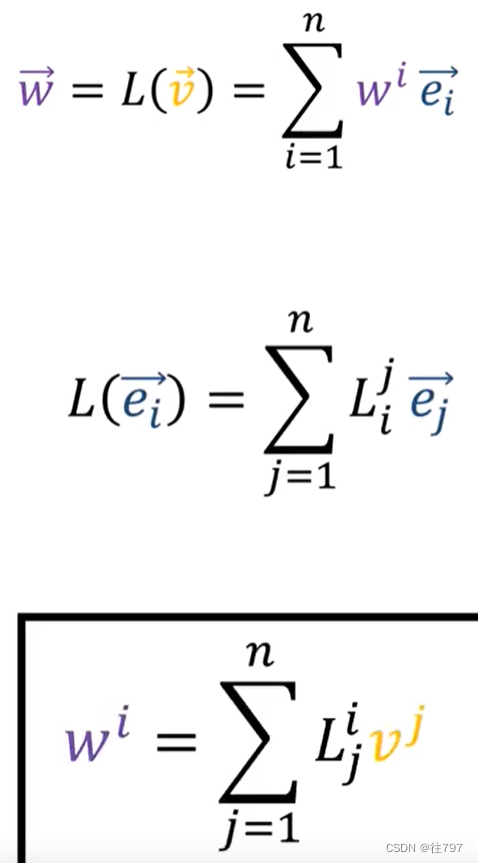
9.Linear Maps
线性映射 线性映射是将向量作为输入并产生一些新向量作为输出的转换。 从坐标定义开始(数组),再到2,3,并展示它们是如何关联的 线性映射的坐标表示最终是矩阵, 1.坐标定义(数组) 列向量是向量的坐标表示…...

大数据Doris(十):添加BE步骤
文章目录 添加BE步骤 一、使用mysql连接 二、添加be...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...
