9.Linear Maps
线性映射
线性映射是将向量作为输入并产生一些新向量作为输出的转换。
从坐标定义开始(数组),再到2,3,并展示它们是如何关联的
线性映射的坐标表示最终是矩阵,
1.坐标定义(数组)
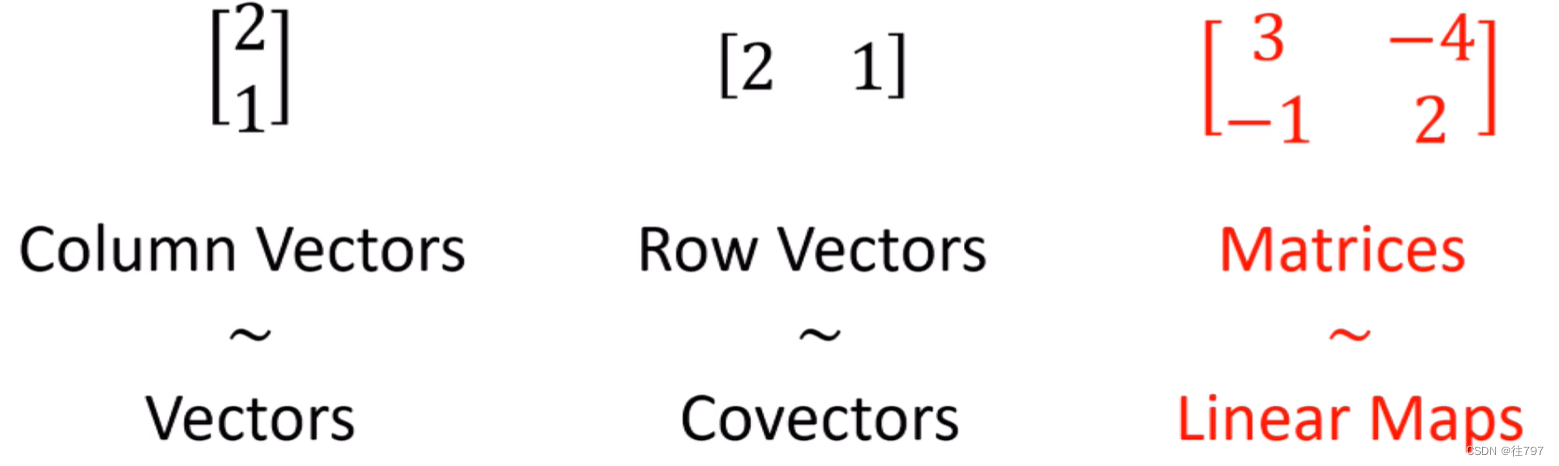
列向量是向量的坐标表示。
行向量是协向量的坐标表示。
矩阵是线性映射的坐标表示。
矩阵是如何转变向量的?
例子
现有一个作用于2x1列向量的2x2矩阵,输出的向量是?
但仅通过查看矩阵中的数字来理解矩阵在做什么会让人感到困惑。
但对所有这些数字的含义,有一个简单的解释:
注意,若使用列向量 作为输入,将得到矩阵的第一列作为输出。
若使用列向量 作为输入, 将得到矩阵的第二列作为输出。
现这些列向量 、
, 它们有点像基向量e1、e2的副本,
之所以说是像副本,是因为这里非常重要的一点:线性映射转换向量,但是线性映射不转换基向量!
因此,当使用线性映射转换向量时,基底是不会变的。 我们不会移动基底,


虽然输出向量可能与输入向量不同,但我们仍将使用相同的基底来测量输出向量,但话虽如此,对于矩阵,第 i 列会告诉你将第 i 个基向量的副本映射到哪里。
因此,从视觉上观察一下,
现有两基底:e1、e2,还有两向量v,w。v和w有点像e1、e2的副本,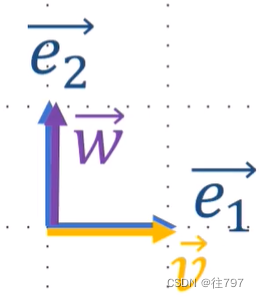
有个矩阵如下:
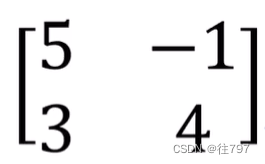
那么该矩阵会将向量v(v像e1的副本)发送到哪?
只看矩阵的第一列,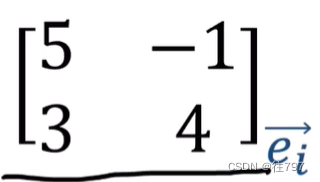
它表示向量5e1+3e2 , 这就是线性映射的输出,![]()
V在视觉上:
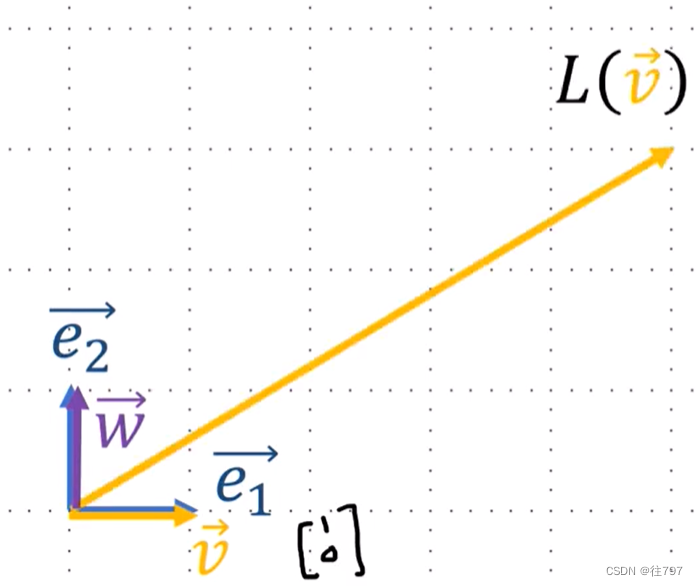
矩阵对向量w(e2的副本)做了什么?
看矩阵的第二列,给我们输出 -e1+4e2
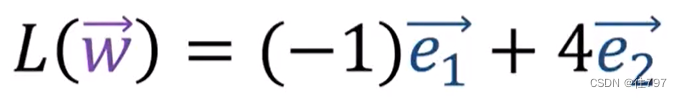
视觉上:
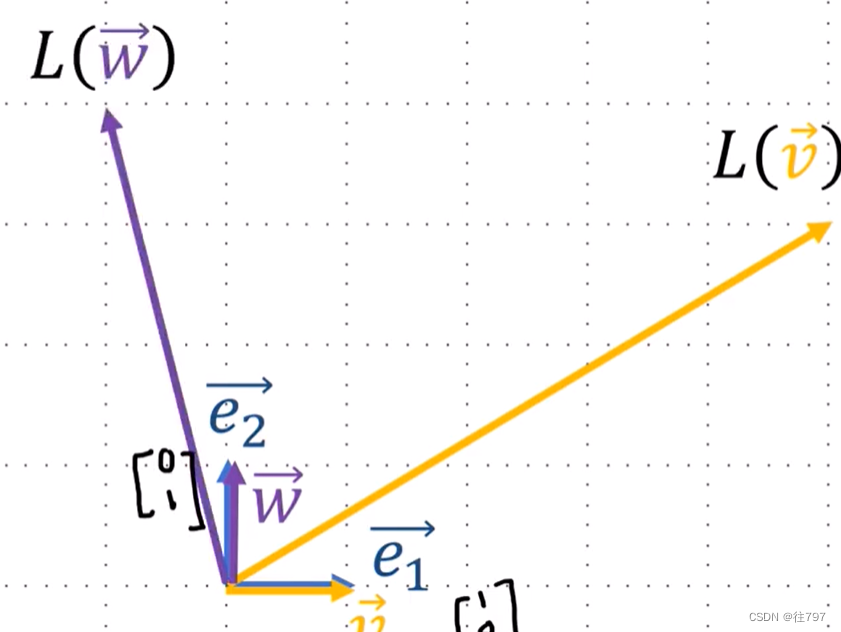
注意到,基向量没有移动,因为线性映射不会改变基底,我们仍用相同的基底测量输出向量,
所以,综上,矩阵是线性映射的坐标解释。
2.几何定义(线性映射视为图片)
线性映射 是 空间转换,并且保持线平行, 保持线间隔均匀,保持原点静止。
为从视觉上了解它的外观,从2D空间开始,上面有一堆网格线:
 (初始的输入空间?)
(初始的输入空间?)
这里有三个线性映射的例子:
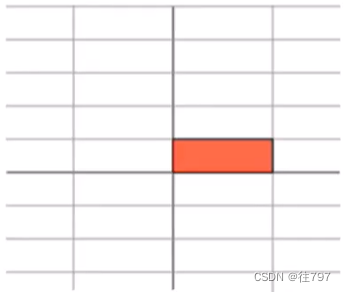
所以,上面这个线性映射基本上只是水平方向的拉伸。
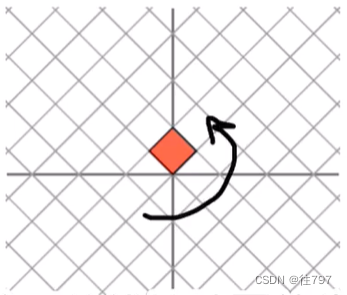 这个线性映射像一个旋转,
这个线性映射像一个旋转,
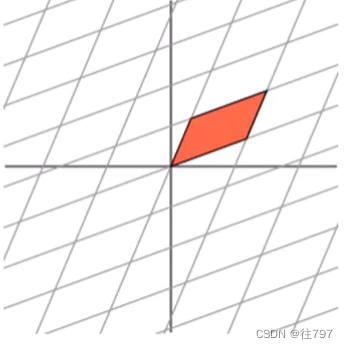
这个线性映射像做一个倾斜变换(可把它想象成在这个方向上做一个旋转,然后沿着这个轴伸展)。
正如上面这些图所示,在所有这些情况下, 输出空间中的网格线仍然彼此平行, 都是均匀分布的(即使间距与输入空间不同),并且原点没有移动。
所有的上面这些都是线性映射可以做到的。
(注意,在该定义下,translation are not linear maps------平移不是线性映射。即使平移能使得网格线平行,间距均匀,但平移会移动原点,所以平移不是线性映射)
所以,这就是可视化的几何定义。
3.抽象定义(纯代数)
线性映射 是将 向量 映射 到 向量 的函数。
在该情况下,现有一映射L将 向量从向量空间V 映射到 向量空间W,我们很多例子涉及到的映射是从空间V映射到 空间V, 但一般来说,输入和输出空间可以不同。
且线性映射在这里遵循两个属性:
1、可添加线性映射的输入或输出并得到相同的答案。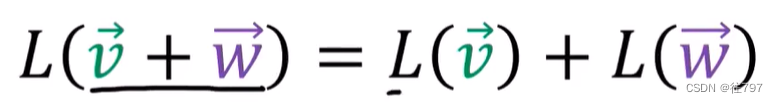
2.可缩放输入或缩放输出并得到相同的答案。
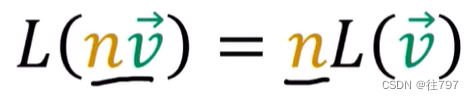
这两个属性被称为“线性”、 。 所以协向量和线性映射都是线性函数。唯一的区别是:协向量输出一个标量,线性映射输出向量。
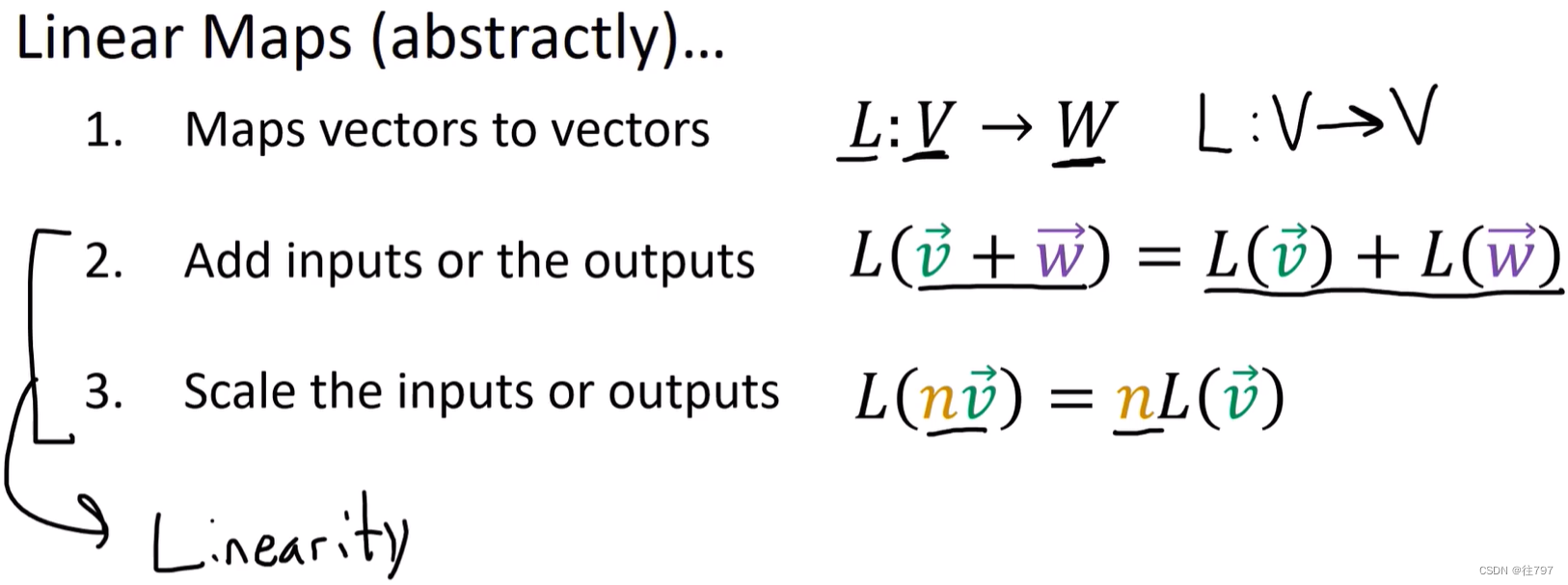
下面展示 这个抽象定义 如何 与我们看到的其他定义相关联。
如前所说,有这个属性:
![]()
现展示它的几何意义,在网格上绘制输入变量,这里我们有绿色的向量v和紫色的向量w,
v+w 用黑色表示。
现展示这图中的三个线性映射是如何服从这个代数性质的。

在这些所有的输出空间中可以看到,加法定律仍然有效,
对缩放规则(第二个属性)也做同样的事情。
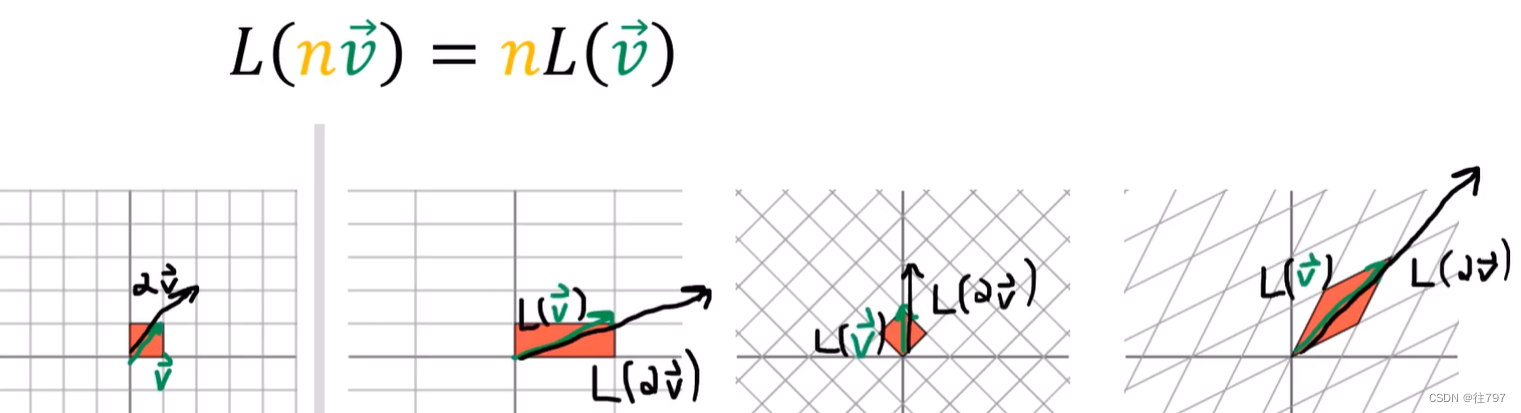
因此,先缩放再转换 与 先转换再缩放 是一回事。
还有一个问题,坐标定义的来源
对于下图这个矩阵乘法公式,若你不知道它背后的原因,它看起来真的很奇怪。
事实证明,矩阵乘法规则实际上来自上面这个抽象定义,
证明:
首先我们有一个线性映射L,它作用于向量V,并产生输出向量W,
若将向量V拓展成它的分量,就能得到
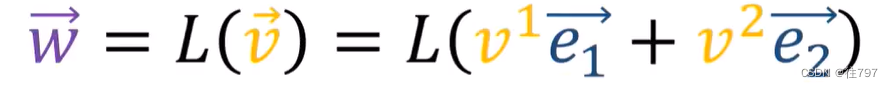
通过L的线性规则,得到: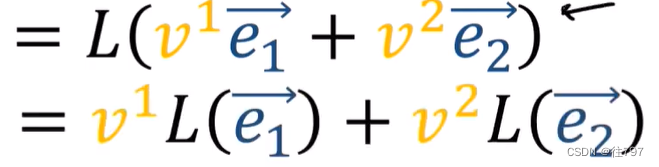
e1、e2是向量,所以你可能会问如何根据 基底e1、e2来表达这些向量,
现做个 简单的假设:
假设线性映射L是从V到V的函数,因此输入空间和输出空间是相同的。
因此,输出空间V仍然具有基底e1、e2,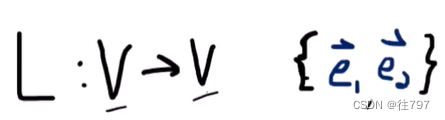
这意味着我们仍然可以将 这些输出向量 写为相同的旧基 e1、e2的线性组合,
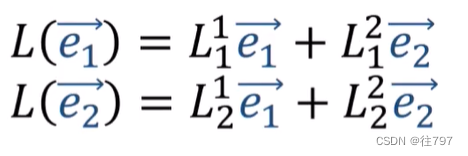
而这些线性组合的系数,
这些L系数帮助我们使用“e”基底向量构建线性映射的输出向量。
所以,可以将输出向量重写为基的线性组合,并且可在此切换内容为以按基向量e1、e2来重新分组,
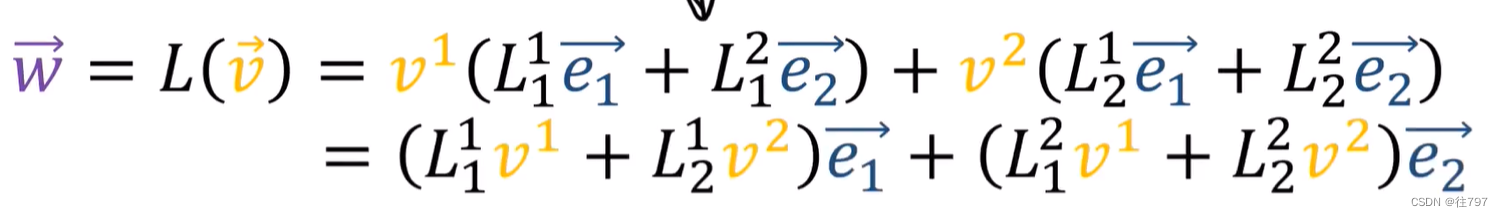
现在,由于将W写成基向量的线性组合,
因此,这些系数 实际上 只是W的分量:w1、w2 ,
所以现在我们已经推到出 如何使用这些公式将V系数转换为W系数,
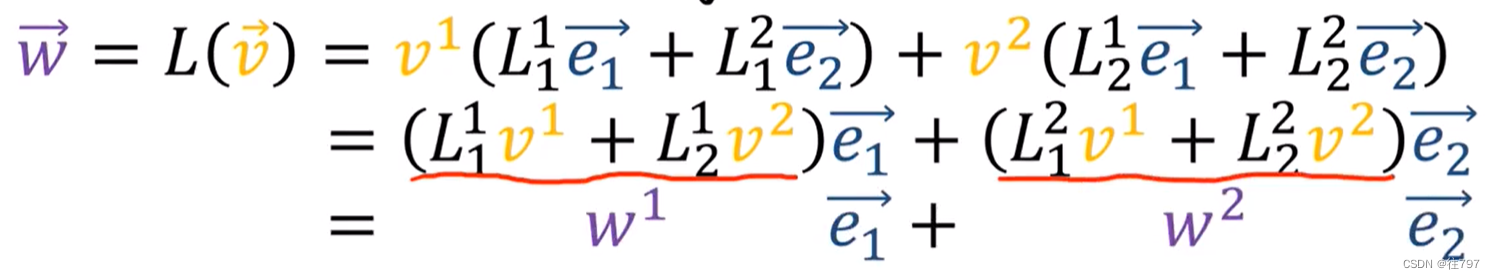
而这些公式 就是那些当你做标准的2x2矩阵乘以一个2x1的列向量。
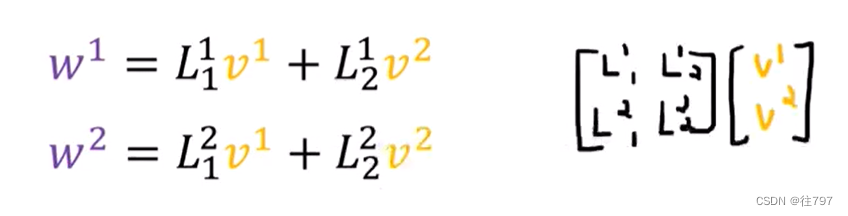
现总结一下,如果我们有一个线性映射L,它可以像这样将向量V转换为另一个向量W,其中W可以写成基底的线性组合,并且我门知道如何使用L系数转换基底(或者说我们知道L如何转换基向量副本可能更好)
这意味着我们可以在这里使用这些公式将V分量变为W分量。
如果对任意数量的维度重复这个论点,如果我们有一个n维的线性映射L,
我们将从这里的公式中得到所有的L系数,然后可以使用这个公式将V分量转换为W分量,

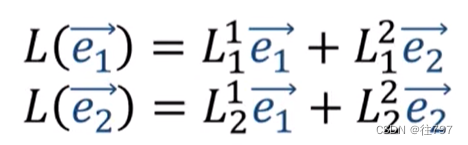
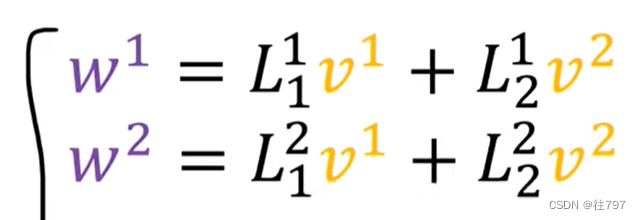
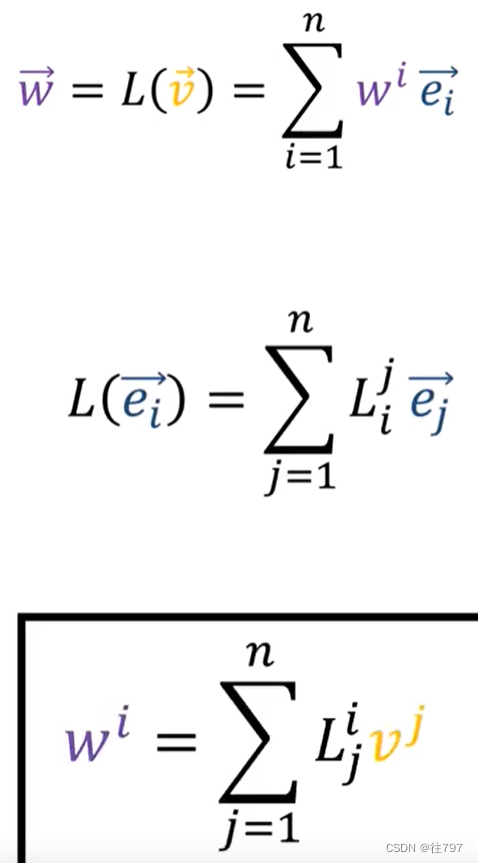
相关文章:
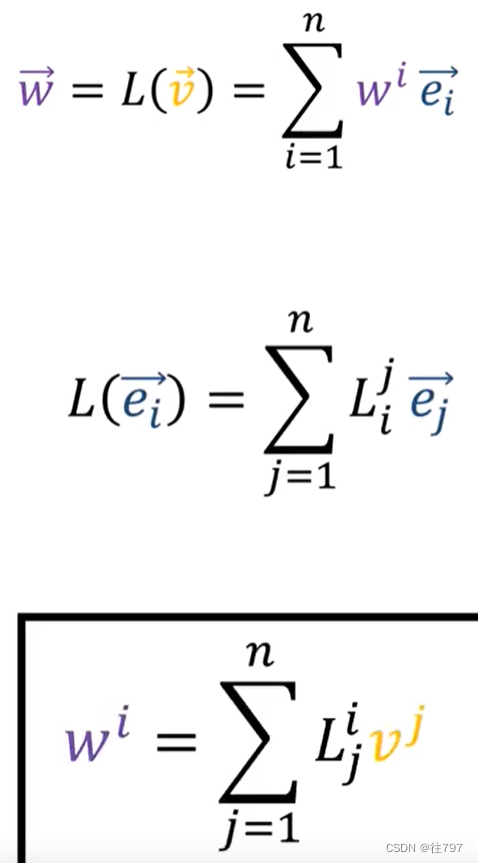
9.Linear Maps
线性映射 线性映射是将向量作为输入并产生一些新向量作为输出的转换。 从坐标定义开始(数组),再到2,3,并展示它们是如何关联的 线性映射的坐标表示最终是矩阵, 1.坐标定义(数组) 列向量是向量的坐标表示…...

大数据Doris(十):添加BE步骤
文章目录 添加BE步骤 一、使用mysql连接 二、添加be...

Vue2 +Element UI 表格行合并
如果相邻数据是一致的,则单元格的行合并,指定需要合并的列,下面我是指定合并了分类和类型这两列。 先看效果 Element UI为我们的<el-table>提供了一个属性span-method:合并行或列的计算方法 下面是一个示例: html部分 - 主要是在表上指…...

SuperEdge易学易用系列-一键搭建SuperEdge集群
条件说明: 系统 公网IP 内网IP 服务器所在地 K8S版本 Centos7.9 114.116.101.254 192.168.0.245 北京 v1.22.6 Centos7.9 119.8.1.96 192.168.0.83 香港 v1.22.6 Ubuntu22 94.74.108.152 192.168.0.154 纽约 v1.22.6 1. 开始部署 1.1 两条指令从零搭建一个边缘集…...
农场养殖农产品商城小程序搭建
鸡鸭羊牛鱼养殖用户不少,其规模也有大有小,尤其对一些生态养殖企业,其产品需求度更高,同时他们也有实际的销售需求。 由于具备较为稳定的货源,因此大规模多规格销售属性很足。 通过【雨科】平台搭建农场养殖商城&…...
大语言模型之十七-QA-LoRA
由于基座模型通常需要海量的数据和算力内存,这一巨大的成本往往只有巨头公司会投入,所以一些优秀的大语言模型要么是大公司开源的,要么是背后有大公司身影公司开源的,如何从优秀的开源基座模型针对特定场景fine-tune模型具有广大的…...
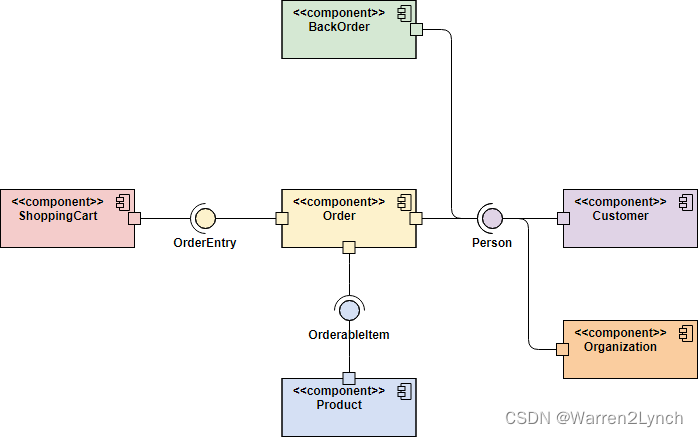
UML组件图综合指南:设计清晰、可维护的软件系统
介绍: UML(Unified Modeling Language)组件图是软件系统设计中的重要工具,用于描绘系统的物理结构和组件之间的关系。在软件工程中,通过创建清晰的组件图,团队能够更好地理解系统的模块化结构和组织关系&a…...
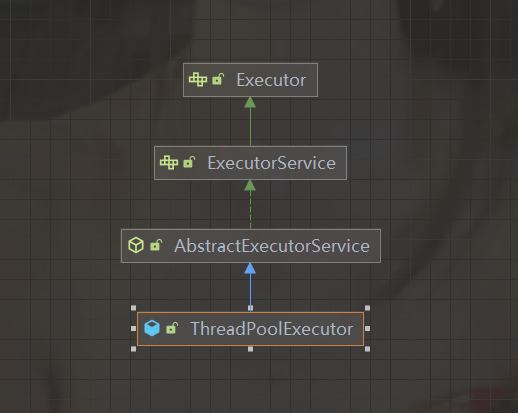
深入浅出ThreadPoolExecutor(一)
文章目录 线程池简诉ThreadPoolExecutor详解ThreadPoolExecutor参数详解创建线程池的工具类Executors 线程池简诉 针对各种池子,比如 连接池:用于管理和重复使用数据库连接,避免频繁创建和销毁数据库连接带来的性能开销。对象池:用于管理和重复使用对象…...

网站的常见攻击与防护方法
在互联网时代,几乎每个网站都存在着潜在的安全威胁。这些威胁可能来自人为失误,也可能源自网络犯罪团伙所发起的复杂攻击。无论攻击的本质如何,网络攻击者的主要动机通常是谋求经济利益。这意味着无论您经营的是电子商务项目还是小型商业网站…...
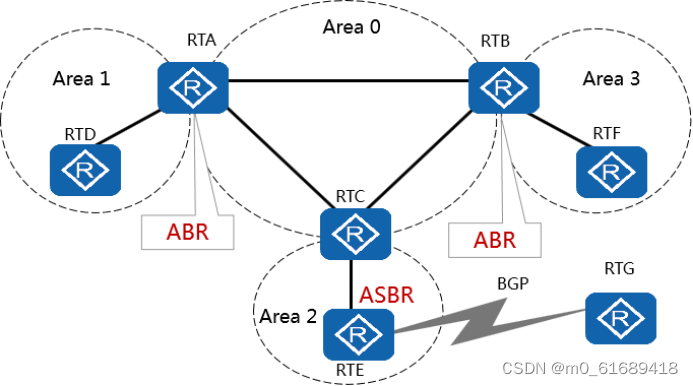
网络工程师知识点3
41、各个路由协议,在华为设备中的优先级? 直连路由 0 OSPF 10 静态 60 42、OSPF:开放式最短路径优先路由协议,使用SPF算法发现和计算路由 OSPF的优点: 1、收敛速度快,无路由自环,适用于大型网络…...
mongoDB 性能优化
文章目录 前言mongoDB 性能优化1. explain方法来查看查询的执行计划2. 查看mongoDB 集合的索引3. mongoDB 怎么添加索引4. 升序索引与降序索引是什么意思 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易…...

10月13日,每日信息差
今天是2023年10月13日,以下是为您准备的13条信息差 第一、欧盟投资4.5亿欧元在法国建设电池超级工厂。欧洲投资银行是欧盟的贷款机构,也是世界上最大的跨国银行之一 第二、北京银行推出数字人民币智能合约平台 数字人民币预付资金管理产品在商超场景…...

Spring Boot 中的 Redis 数据操作配置和使用
Spring Boot 中的 Redis 数据操作配置和使用 Redis(Remote Dictionary Server)是一种高性能的开源内存数据库,用于缓存、消息队列、会话管理和数据存储。在Spring Boot应用程序中,Redis被广泛用于各种用例,包括缓存、…...

rust宏
宏看起来和函数很像,只不过名称末尾有一个感叹号 ! 。 宏并不产生函数调用,而是展开成源码,并和程序的其余部分一起被编译。 Rust宏和C不同,Rust的宏会展开为抽象语法树(AST,abstract syntax treeÿ…...
性能测试之性能测试指标详解
前言 刚开始,以为做性能测试,就是做些脚本、参数化、关联,压起来之后,再扔出一个结果。 但实际上不止这些内容,还要加上性能分析,关注调优之后响应时间有多大的提升,TPS 有多大的提高…...

CustomNavBar 自定义导航栏视图
1. 创建偏好设置键 CustomNavBarTitlePreferenceKey.swift import Foundation import SwiftUI//State private var showBackButton: Bool true //State private var title: String "Title" //"" //State private var subtitle: String? "SubTitl…...

canal rocketmq
上篇文章canal 消费进度说到直接使用ClusterCanalConnector并发消费是有问题的,可以先用单点将canal事件发送到mq中,再由mq并发处理,另外mq还可以做到削峰的作用,让canal数据不至于阻塞。 使用队列,可以自己起一个单实…...
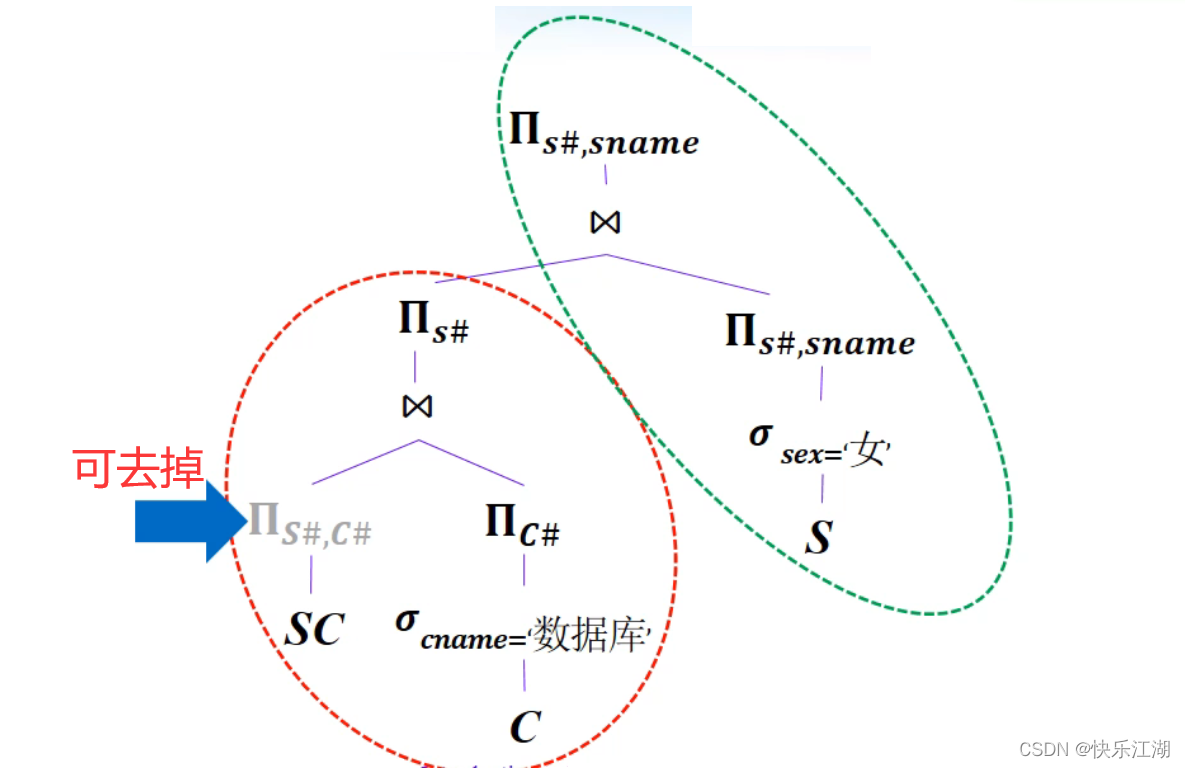
【数据库系统概论】第九章关系查询处理何查询优化
9.1查询处理 一:查询处理步骤 关系数据库管理系统查询处理可以分为4个阶段: 查询分析查询检查查询优化查询执行 (1)查询分析 任务:对查询语句进行扫描,分析词法、语法是否符合SQL语法规则 如果没有语…...

bp盐丘模型波场数值模拟matlab
波场数值模拟是地震勘探和地震学研究中常用的工具,而BP(Backpropagation)盐丘模型是一种用于地下介质成像的方法。如果您想在MATLAB中进行波场数值模拟,并结合BP盐丘模型进行地下成像,可以按照以下步骤进行:…...
结构体对齐规则
1.第一个成员在结构体变量偏移量为0的地址处。 2.其他成员变量对齐到某个数字(对齐数)的整数倍的地址处。(对齐数编译器默认的一个对齐数与该成员大小的较小值)注意:目前有且只有VS编译器有默认为8. 3.结构体总大小为最大对齐数的整数倍。 4.如果嵌套…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
