[GAMES101]透视投影变换矩阵中为什么需要改变z值
一、问题提出
在GAMES101-Lecture4 Transformation Matrices 一节中,闫老师介绍了正交投影和透视投影。
在讲透视投影变换矩阵 M p e r s p → o r t h o M_{persp→ortho} Mpersp→ortho时,同学们对矩阵中的z分量是变化的还是不变的有很多争论。即下图中z分量经过投影变换后的z'底是保持不变依旧等于z,还是"unknown"大家有不同的看法。基于查阅的资料,我将在本文中谈一下自己对于这个问题的理解,并对投影变换矩阵的计算公式进行解释。

二、投影变换
1. 正交投影 Orthographic Projection
(1). 正交投影目标:
将指定立方体内部的点映射(变换)到正则立方体(canonical cube) 内。正则立方体是一个中心点在原点,(x,y,z)三个分量都在[-1,1]范围内的正方体。
如将下图所示,左侧立方体内部的点,先经过平移(Translate),再经过放缩(Scale)变换后,即可投影到正则立方体内。

(2). 正交投影矩阵 M o r t h o M_{ortho} Mortho:
正交投影矩阵可以由平移矩阵和放缩矩阵相乘得到:

2. 透视投影
(1). 透视投影目标:
将视体内部的点映射(变换)到**正则立方体(canonical cube)**内。视体 通常是一个 方平截头体,可由fov, aspect_ratio, zNear和zFar这几个参数确定。
如下图所示:

(2). 透视投影步骤:
前面已经简单介绍过正交投影了,正交投影相对简单,只要进行平移+放缩两次变换即可得到。透视投影 相对复杂,
透视投影包含两步:
- 将视体变换为立方体, First “squish” the frustum into a cuboid (n -> n, f -> f) ( M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho) ;
- 进行正交投影,将立方体变换到正则立方体,Do orthographic projection ( M o r t h o M_{ortho} Mortho);
为什么不直接使用平移+放缩+非仿射变换 求得透视投影矩阵,而是需要先将透视投影转为立方体,再进行一次正交投影这两步(这两步称之为透视规范化)?
这是因为:
- 规范化使得只需要一个流水线体系就可以进行透视投影和正交投影;
- 尽可能位于四维齐次空间中,以便保持隐藏面消除和明暗处理所需要的三维信息。透视投影的第一步将视体转到立方体依旧保持各点的z分量信息,便于之后进行深度处理等操作;
- 简化了裁剪的操作。第一步转为立方体后,由于立方体的边都与世界坐标系的x,y,z轴平行,因此可以方便地裁剪掉立方体外的点;
(3). 透视投影矩阵:
在计算透视投影矩阵之前需要明确一点:目标投影矩阵M必须是一个固定的矩阵,针对视体内的任何一点,都使用相同的一个矩阵,条件(1)。
我们称第一步中从视体变换到立方体的矩阵 M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho为透视规范化矩阵。
对于空间内的点(x,y,z)(这里的x,y,z是变量,因为空间需要进行投影变换的点不只一个),其变换后的点为(x',y',z')。
其中:
x ′ = n z x , y ′ = n z y , z ′ = ? x'=\frac{n}{z}x, y'=\frac{n}{z}y, z'=? x′=znx,y′=zny,z′=?
a. 假设令z'不变:
即:
x ′ = n z x , y ′ = n z y , z ′ = z x'=\frac{n}{z}x, y'=\frac{n}{z}y, z'=z x′=znx,y′=zny,z′=z
我们可以逆向算出对应的透视规范化矩阵 M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho
M p e r s p → o r t h o = ( n / z 0 0 0 0 n / z 0 0 0 0 1 0 0 0 0 1 ) M{persp→ortho} = \begin{pmatrix} n/z & 0 & 0 & 0 \\ 0 & n/z & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} Mpersp→ortho= n/z0000n/z0000100001
矩阵中n=zNear是一个常数,然而矩阵中的z是一个变量(即n/z中的z),对于视体中的每一个不同的点,都需要一个特定的z值,这并不满足条件(1),不是我们想要的,我们想要一个固定的、不随目标点变化的矩阵。
b. 假设令z'改变:
根据a.中的分析可以得出,假如令z'=z,那么对于视体中的每个点都需要一个透视规范化矩阵M,不能满足条件(1)。
因此我们需要令透视正则变换后的各点z'值发生变化,以消除透视规范化矩阵M中的变量z。
一个简单的方式是,我们先假设此时不知道z'等于什么,并令x',y'和齐次坐标中的w'都乘以z。那么 透视规范化矩阵 M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho 可以写为:
M p e r s p → o r t h o = ( n 0 0 0 0 n 0 0 ? ? A B 0 0 1 0 ) M{persp→ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & A & B\\ 0 & 0 & 1 & 0 \end{pmatrix} Mpersp→ortho= n0?00n?000A100B0
另外由于在投影变换后还需要进行阴影遮挡判断、隐藏面消除和明暗处理等操作,因此我们需要保证原始空间中z值小的点,在投影正则化变换后的z'值依旧小,原始空间中z值大的点,在投影正则化变换后的z'值依旧大,条件(2)。
条件(2)也说明,z'只能跟原始点齐次坐标中的z和w相关,跟x,y无关,因此可以得到那么透视规范化矩阵 M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho 可以写为:
M p e r s p → o r t h o = ( n 0 0 0 0 n 0 0 0 0 A B 0 0 1 0 ) M{persp→ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & B\\ 0 & 0 & 1 & 0 \end{pmatrix} Mpersp→ortho= n0000n0000A100B0
除此以外,我们还需要令原来在z=zNear平面上的点,经过变换后依旧在z=zNear平面上,原来在z=zFar平面上的点依旧在z=zFar平面上。这是因为,我们需要保证 边界上的点变换后依旧在边界上,条件(3)。
假如不能保证满足条件(3),那么在经过投影正则化变化后,有可能原来在zFar外面的点,在变换后到了立方体内了!原本 视体 外需要被裁剪掉的点,变换到了立方体内,这可能导致裁剪错误。
因此根据条件(3),可以得到下面两个公式:
( 0 0 A B ) ∗ ( x y n 1 ) = n 2 (0\ 0\ A\ B) * \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = n^2 (0 0 A B)∗ xyn1 =n2
同时:
( 0 0 A B ) ∗ ( x y f 1 ) = f 2 (0\ 0\ A\ B) * \begin{pmatrix} x \\ y \\ f \\ 1 \end{pmatrix} = f^2 (0 0 A B)∗ xyf1 =f2
根据这两个公式即可求得
A = n + f , B = − n f A=n+f, B=-nf A=n+f,B=−nf
这就是投影变换中 M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho的由来。
3. 总结
投影变换的目标是:根据给出的 视体 参数(fov, aspect_ratio, zNear, zFar等参数),计算得到一个投影变换矩阵M,这个矩阵需要满足三个条件:
条件(1),这个矩阵是唯一固定的,即这个矩阵中的元素值只跟视体相关,跟视体中点的坐标无关;条件(2),经过变换后,必须保证各个点的z值相对关系不变,即假如点a的z值大于点b的z值,那么经过变换点a的z'依旧大于点b变换后的z'。那么z'不能与(x,y,z,w)中的x,y相关,只能由z,w确定;条件(3),视体边界面z=zNear平面和z=zFar平面上点的经过变换后依旧在立方体边界面上;
为了满足条件(1):z'不能等于z(除了z=zNear和z=zFar平面上的点)。
为了满足条件(2): M p e r s p → o r t h o M{persp→ortho} Mpersp→ortho第三行 ( ? ? A B ) (?\ ?\ A\ B) (? ? A B) 前两个元素需要等于0。
为了满足条件(3): A = n + f , B = − n f A=n+f, B=-nf A=n+f,B=−nf。
三、参考
1.计算机图形学第六章观察-黄章进-中国科学技术大学
2.GAMES101-Lecture 4:Transformation Matrices
相关文章:

[GAMES101]透视投影变换矩阵中为什么需要改变z值
一、问题提出 在GAMES101-Lecture4 Transformation Matrices 一节中,闫老师介绍了正交投影和透视投影。 在讲透视投影变换矩阵 M p e r s p → o r t h o M_{persp→ortho} Mpersp→ortho时,同学们对矩阵中的z分量是变化的还是不变的有很多争论。即下…...

sklearn处理离散变量的问题——以决策树为例
最近做项目遇到的数据集中,有许多高维类别特征。catboost是可以直接指定categorical_columns的【直接进行ordered TS编码】,但是XGboost和随机森林甚至决策树都没有这个接口。但是在学习决策树的时候(无论是ID3、C4.5还是CART)&am…...

QT 数据库表格----QSqlTableModel
将数据库数据以表格的形式转化处理的方法很多,但我觉得QSqlTableModel这个model应算是非常好用的; msql.exec("create table alldata(照片,车牌号 "",入车时间,出车时间,金额,状态,看守人员);"); //创建表格 //msql 打开的数据库即Q…...

Vue_Bug Failed to fetch extension, trying 4 more times
Bug描述: 启动electron时出现Failed to fetch extension, trying 4 more times的问题 解决方法: 去src/background.js文件中进行代码注释工作 app.on(ready, async() > {// if (isDevelopment && !process.env.IS_TEST) {// // Install V…...

缩短从需求到上线的距离:集成多种工程实践的稳定框架 | 开源日报 No.55
zeromicro/go-zero Stars: 25.7k License: MIT go-zero 是一个集成了各种工程实践的 web 和 rpc 框架。通过弹性设计保障了大并发服务端的稳定性,经受了充分的实战检验。 go-zero 包含极简的 API 定义和生成工具 goctl,可以根据定义的 api 文件一键生成…...

基于秃鹰优化的BP神经网络(分类应用) - 附代码
基于秃鹰优化的BP神经网络(分类应用) - 附代码 文章目录 基于秃鹰优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.秃鹰优化BP神经网络3.1 BP神经网络参数设置3.2 秃鹰算法应用 4.测试结果:5.M…...
C++笔记之std::future的用法
C笔记之std::future的用法 code review! 文章目录 C笔记之std::future的用法1.C中std::future和std::async总是一起出现吗?2.主要特点和用法3.一个完整的例子4.std::future 存放的是一个结果吗?5.cppreference——std::future 1.C中std::future和std::a…...
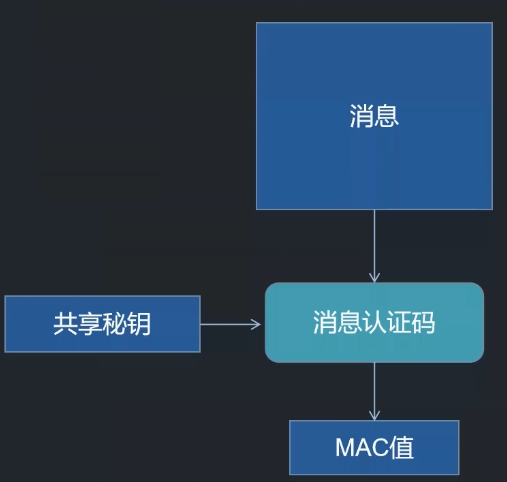
openssl学习——消息认证码原理
消息认证码原理 消息认证码(Message Authentication Code, MAC)是一种技术,它的原理是通过对消息和密钥进行特定的处理,生成一个固定长度的数据,这个数据就是消息认证码(MAC)。这个过程可以看作…...

Netty使用SslHandler实现加密通信-单向认证篇
引入依赖 <dependency><groupId>io.netty</groupId><artifactId>netty-all</artifactId><version>4.1.100.Final</version> </dependency>生成keystore.jks文件 keytool -genkeypair -alias your_alias -keyalg RSA -keysto…...

Jetpack:007-Kotlin中的Button
文章目录 1. 概念介绍2. 使用方法2.1 Button2.2 IconButton2.3 ElevatedButton2.4 OutlinedButton2.5 TextButton2.6 FloatingActionButton 3. 示例代码4. 内容总结 我们在上一章回中介绍了Jetpack中输入框相关的内容,本章回中将要介绍 Button。闲话休提࿰…...
opencv图形绘制2
目录 制作宣传语(中文) 制作宣传语(英文) 绘制标记 鼠标交互绘制十字线 鼠标交互绘制图形 鼠标交互制作几何画板 滚动条控制 鼠标事件练习 制作宣传语(中文) import cv2 import numpy as np from …...
(续))
“华为杯”研究生数学建模竞赛2019年-【华为杯】A题:无线智能传播模型(附优秀论文及Pyhton代码实现)(续)
目录 六、问题三的分析与建模 6.1 问题三的分析 6.2 问题三的建模 6.2.1 模型介绍...
爬虫 | 正则、Xpath、BeautifulSoup示例学习
文章目录 📚import requests📚import re📚from lxml import etree📚from bs4 import BeautifulSoup📚小结 契机是课程项目需要爬取一份数据,于是在CSDN搜了搜相关的教程。在博主【朦胧的雨梦】主页学到很多…...
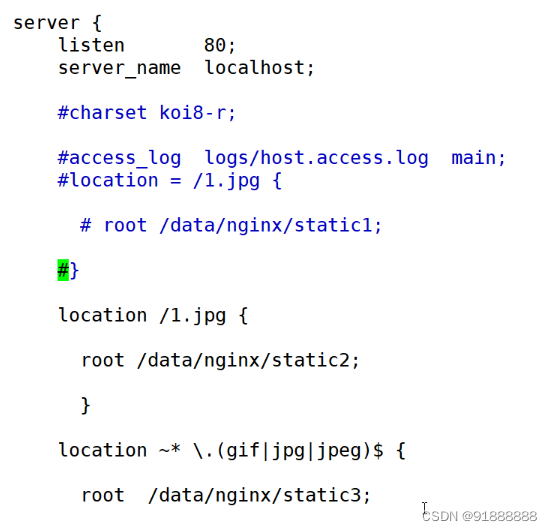
nginx的location的优先级和匹配方式
nginx的location的优先级和匹配方式 在http模块中有server,server模块中有location,location匹配的是uri 在一个server中,会有多个location,如何来确定匹配哪个location niginx的正则表达式 ^ 字符串的起始位置 $ 字符串的…...

深入了解Spring Boot Actuator
文章目录 引言什么是ActuatorActuator的底层技术和原理端点自动配置端点请求处理端点数据提供端点数据暴露 如何使用Actuator添加依赖访问端点自定义端点 实例演示结论 引言 Spring Boot Actuator是一个非常强大且广泛使用的模块,它为Spring Boot应用程序提供了一套…...

【SQL】NodeJs 连接 MySql 、MySql 常见语句
1.安装 mysql npm install mysql 2.引入MySql import mysql from mysql 3.连接MySql const connection mysql.createConnection({host: yourServerip,user: yourUsername,password: yourPassword,database: yourDatabase })connection.connect(err > {if (err) {console…...

SSH 基础学习使用
什么是SSH 1.SSH SSH(Secure Shell) 是较可靠,专为远程登录会话和其他网络服务提供安全性的协议,利用 SSH 协议可以有效防止远程管理过程中的信息泄露问题。 实际应用中,主要用于保证远程登录和远程通信的安全&#…...
JavaFX: 使用本地openjfx包
JavaFX: 使用本地openjfx包 1、注释配置2、下载openjfx包3、导入openjfx的jar包 1、注释配置 build.gradle配置注释: 2、下载openjfx包 下载javaFx地址:https://gluonhq.com/products/javafx/ 3、导入openjfx的jar包...
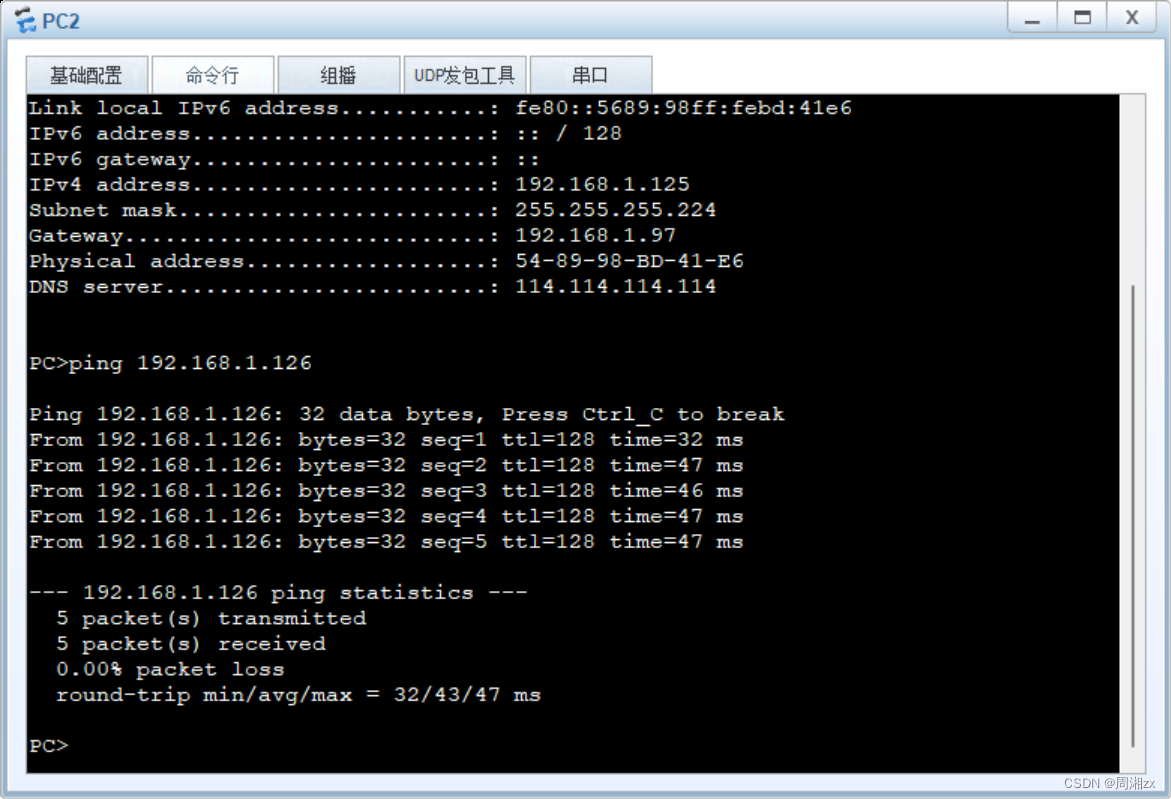
【HCIA】静态路由综合实验
实验要求: 1、R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址之后不能再对其进行任何配置 2、R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配 3、R1、R2、R4,各有两个环回IP地址;R5,R6各有一…...
Django框架集成Celery异步-【2】:django集成celery,拿来即用,可用操作django的orm等功能
一、项目结构和依赖 study_celery | --user |-- models.py |--views.py |--urls.py |--celery_task |--__init__.py |--async_task.py |-- celery.py | --check_task.py | --config.py | --scheduler_task.py | --study_celery | --settings.py | --manage.py 依赖:…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
