算法练习13——跳跃游戏II
LeetCode 45 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
动态规划
dp[j]为跳到i位置所需的最少次数
实测能过但是耗时很高,恰好数据集各项数量级每超出限制,但凡0 <= nums[i] <= 1000加一点估计都过不了
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
class Solution:def jump(self, nums: List[int]) -> int:length = len(nums)if length == 1:return 0dp = [sys.maxsize] * lengthdp[0] = 0for i in range(length):for j in range(i + 1, min(i + nums[i] + 1, length)):dp[j] = min(dp[j], dp[i] + 1)return dp[length - 1]
转换问题 + 蛮力法
class Solution:def jump(self, nums: List[int]) -> int:n = len(nums)maxPos, end, step = 0, 0, 0for i in range(n - 1):if maxPos >= i:maxPos = max(maxPos, i + nums[i])if i == end:end = maxPosstep += 1return step# 作者:力扣官方题解
# 链接:https://leetcode.cn/problems/jump-game-ii/
# 来源:力扣(LeetCode)
# 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
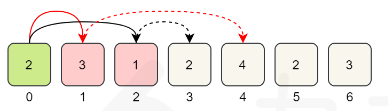
以上是官方贪心解法,感觉并不足够“贪心”,更像是暴力解法,结合上图说一下我的理解:
- 首先一定能到,那么最多就n-1次跳跃,所以遍历每一次跳跃情况
- 第一次跳跃,发现可以跳到1、2,没到n-1,那么必然会【跳到1或2】,跳跃次数+1
- 第二次跳跃,会从1或2跳,可选位置,从1出发有2、3、4,从2出发有3,综合来看就是2、3、4,但是显然第一次就可以跳到2,第二次的2就可以忽略,实际上本次可忽略的位置就是本次可以跳到但是上次本就可以跳到的地方,而可忽略的位置由上次可以跳到的最远距离决定,第二次跳跃可忽略2本身及之前的位置,所以第二次跳跃【结果为3或4】,跳跃次数+1
- 第三次跳跃,会从3或4跳,同理,从3可以跳到4、5,从4可以跳到5、6,综合可以到达4、5、6,忽略4,跳跃结果为【5或6】,显然此时就求出来了
代码写法上,应该有两层循环,第一层循环枚举的最多n-1次的跳跃次数,第二层循环,每一次跳跃中的可选位置,巧的是,把所有可选位置连起来正好是一次数组遍历,所以一层循环就可以搞定
如果将end理解为本次跳跃中可忽略数值的上限,maxPos理解为下次跳跃中可忽略数值的上限(需要由本次跳跃备选项进行遍历计算得出),一切则和官方算法一致,或许if maxPos >= i还可省略
class Solution:def jump(self, nums: List[int]) -> int:n = len(nums)maxPos, end, step = 0, 0, 0for i in range(n - 1):maxPos = max(maxPos, i + nums[i])if i == end:end = maxPosstep += 1return step
相关文章:

算法练习13——跳跃游戏II
LeetCode 45 跳跃游戏 II 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返回…...

算法|每日一题|只出现一次的数字|位运算
136.只出现一次的数字 力扣每日一题:136.只出现一次的数字 之前整理过本题及其扩展,详细说明了思路和做法,链接如下: 只出现一次的数字I,II,III 给你一个 非空 整数数组 nums ,除了某个元素只出…...
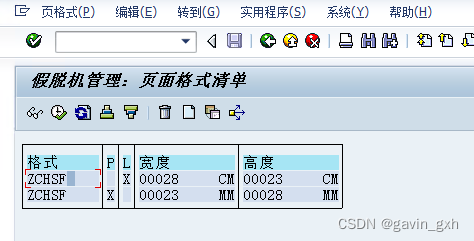
Smartforms 打印出现的问题
上半年ECC做了升级 程序代码从ECC迁移到S4 有用户反馈 打印不能用了 经过调试发现在打印程序中 竟然返回2,但是 smartforms ZRPT_CO_YFLL_DY又是存在的 。 然后去激活 并与 ECC对比发现问题 S4的页大小竟然这么小 找到对应的页格式 对比ECC和S4 果然是这个…...
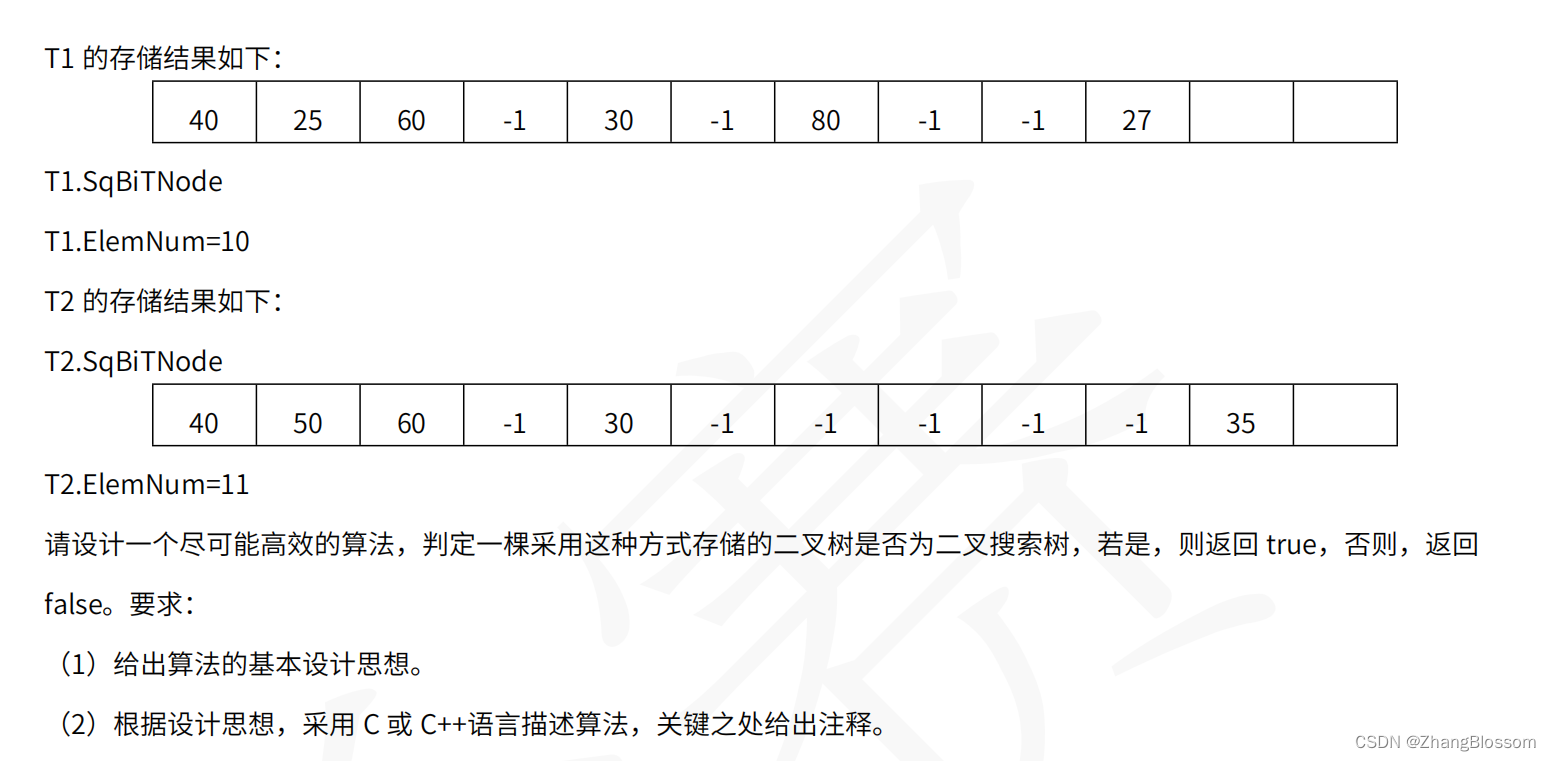
【考研408真题】2022年408数据结构41题---判断当前顺序存储结构树是否是二叉搜索树
文章目录 思路408考研各数据结构C/C代码(Continually updating) 思路 很明显,这是一个顺序存储结构的树的构成方法。其中树的根节点位置从索引0开始,对于该结构,存在有:如果当前根节点的下标为n,…...
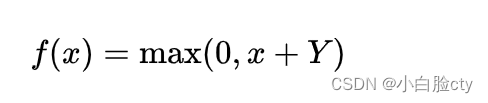
深度学习DAY3:激活函数
激活函数映射——引入非线性性质 h (Σ(W * X)b) yσ(h) 将h的值通过激活函数σ映射到一个特定的输出范围内的一个值,通常是[0, 1]或[-1, 1] 1 Sigmoid激活函数 逻辑回归LR模型的激活函数 Sigmoid函数࿰…...
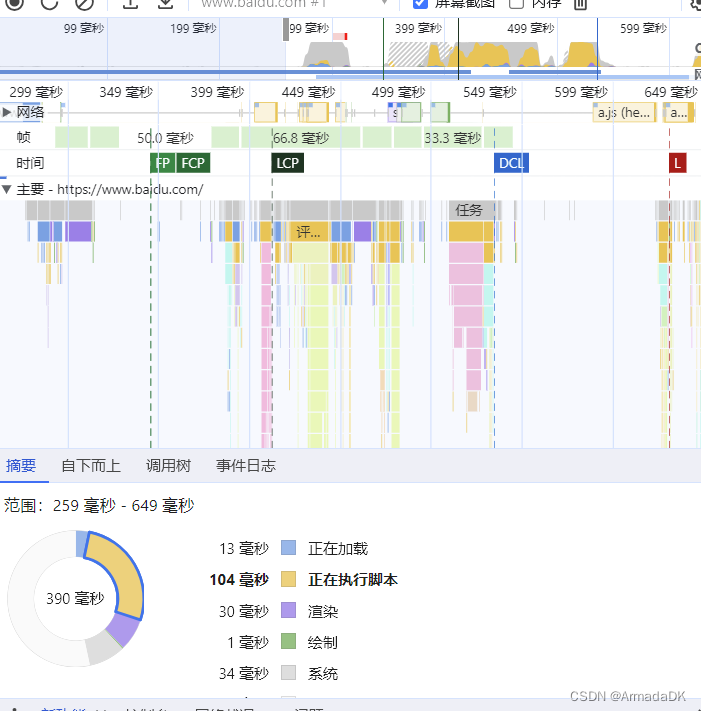
puppeteer
目录 介绍启动方法功能一、爬虫优势如何实现爬虫小demo 功能二、执行脚本百度搜索脚本demo 功能三、获取cookie(这个只能是模拟浏览器当前进入网页的cookie不是平时用的下载的的浏览器的cookie)功能四、监控网页,进行性能分析 介绍 puppetee…...
执行异步HTTP(Ajax)请求的方法($.get、$.post、$getJSON、$ajax))
javascript二维数组(21)执行异步HTTP(Ajax)请求的方法($.get、$.post、$getJSON、$ajax)
执行异步HTTP(Ajax)请求的方法 . g e t 、 .get、 .get、.post、 g e t J S O N 、 getJSON、 getJSON、ajax都是jQuery提供的用于执行异步HTTP(Ajax)请求的方法。每个方法都有其特定的用途和区别。 . g e t :这个方法…...
)
TypeScript React(下)
目录 TypeScript & React TS开发环境的搭建 tsconfig.json webpack.config.js babel.config.js .eslintrc.js TypeScript & React TS开发环境的搭建 软件版本:TypeScript:3.9.5;React:16.13.1 Node:8.17.0环境搭建:正确搭建一…...

『Linux小程序』进度条
文章目录 缓冲区问题回车与换行的区别进度条小程序 缓冲区问题 假设有一段代码为: #include<iostream> #include<unistd.h> int main() …...
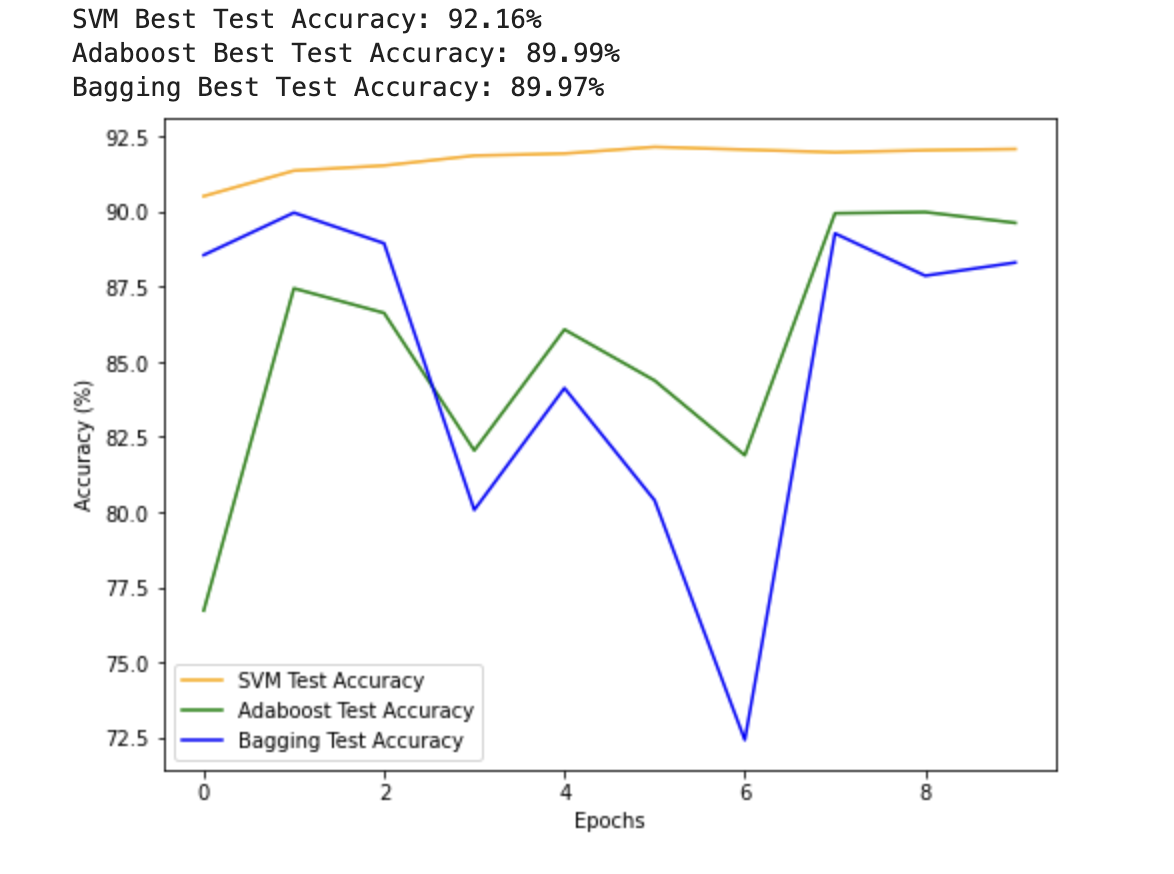
【手写数字识别】GPU训练版本
SVM Adaboost Bagging 完整代码 I import torch import torch.nn.functional as F from torch.utils.data import DataLoader, TensorDataset from torchvision import transforms, datasets import matplotlib.pyplot as plt# 超参数 batch_size 64 num_epochs 10# 数据…...
c#-特殊的集合
位数组 可观察的集合 private ObservableCollection<string> strList new ObservableCollection<string>();// Start is called before the first frame updatevoid Start(){strList.CollectionChanged Change;strList.Add("ssss");strList.Add("…...

Android 使用 eChart 设置标线
echart使用标线 Android部分: import android.webkit.WebView; import com.jianqu.plasmasterilizer.R; import com.jianqu.plasmasterilizer.utils.DisplayUtils; import com.jianqu.plasmasterilizer.utils.TimerUtil; import java.util.ArrayList; import java.…...

红队专题-Cobalt strike 4.x - Beacon重构
红队专题 招募六边形战士队员重构后 Beacon 适配的功能windows平台linux和mac平台C2profile 重构思路跨平台功能免杀代码部分sysinfo包packet包config.go命令的执行shell、run、executepowershell powerpick命令powershell-importexecute-assembly 堆内存加密字符集 招募六边形…...

一文掌握 Go 文件的写入操作
前言 通过案例展示如何读取文件里的内容。本文接着上篇文章的内容,介绍文件的写入操作。 File.Write、File.WriteString、File.WriteAt File.Write(b []byte) (n int, err error) 直接操作磁盘往文件里写入数据,写入单位为字节。 b 参数:…...

小程序入门及案例展示
目录 一、小程序简介 1.1 为什么要使用小程序 1.2 小程序可以干什么 二、前期准备 2.1 申请账号 2.2 开发工具下载与安装 三、电商案例演示 四、入门案例 4.1 项目结构解析 4.2 基础操作及语法 4.3 模拟器 4.4 案例演示 4.4.1 新建页面 4.4.2 头部样式设置 4.4.…...
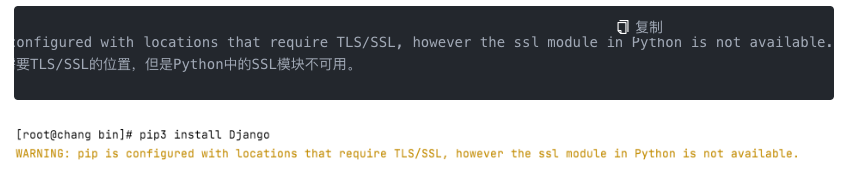
linux 安装python django pip 遇到的问题
Python解决SSL不可用问题 解决方案: 首先要明白python版本需要和openssl的版本需要相对匹配的,在Python3.7之后的版本,依赖的openssl,必须要是1.1或者1.0.2之后的版本,或者安装了2.6.4之后的libressl,linux…...
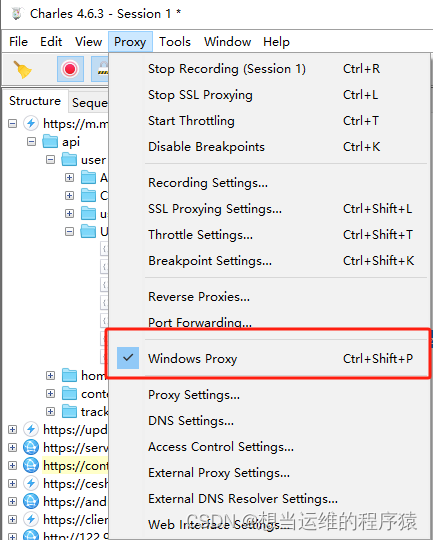
【问题解决】【爬虫】抓包工具charles与pycharm发送https请求冲突问题
问题: 开启charles抓包,运行pycharm发送https请求报以下错误 解决: 修改python代码,发送请求时添加verify false,此时charles也能抓取到pycharm发送的请求 2. 关闭charles抓包,取消勾选window proxy...
:HDFS的定义及概述)
Hadoop3教程(二):HDFS的定义及概述
文章目录 (40)HDFS产生的背景和定义(41)HDFS的优缺点(42)HDFS组成架构(43)HDFS文件块大小(面试重点)参考文献 (40)HDFS产生的背景和定…...
【物联网+JAVA 】智慧工地源码
一、什么是智慧工地? 工地本身不拥有智慧,工地的运作是依赖于人的智慧。工地信息化技术,能够减少对人的依赖,使工地拥有智慧。 智慧工地,就是立足于“智慧城市”和“互联网”,采用云计算、大数据和物联网…...
001数据安全传输-多端协议传输平台:Openssl安装和配置 - EVP代码测试
001数据安全传输-多端协议传输平台:Openssl安装和配置 - EVP代码测试 文章目录 001数据安全传输-多端协议传输平台:Openssl安装和配置 - EVP代码测试1. 安装1.1 windows下安装openssl1.2 Linux下安装OpenSSL 2. VS中使用openssl3. 测试 1. 安装 1.1 win…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
