课题学习(七)----粘滑运动的动态算法
一、 粘滑运动的动态算法
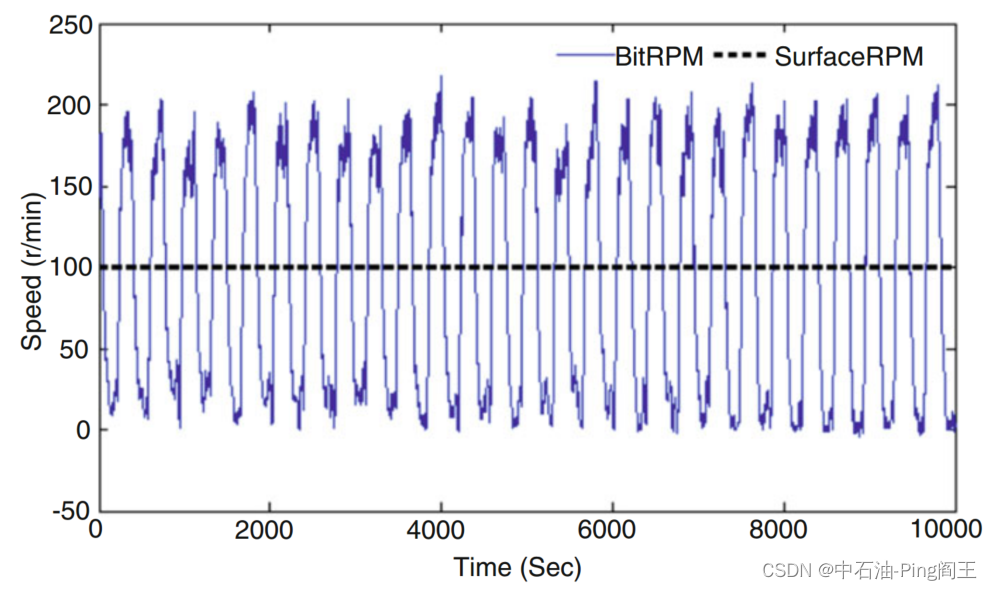
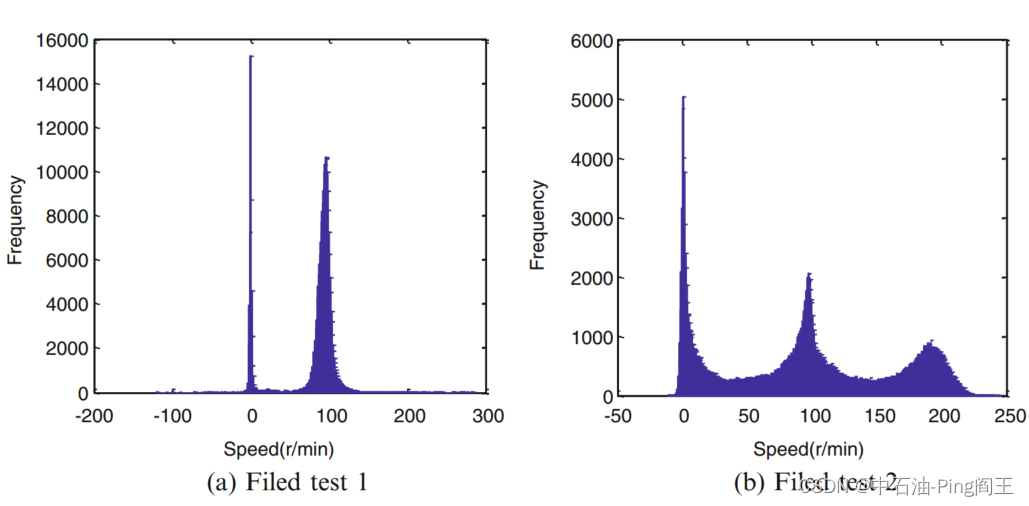
在实际钻井过程中,钻柱会出现扭振和粘滑现象(粘滑运动–B站视频连接),但并不总是呈现均匀旋转。如下图所示,提取一段地下数据时,转盘转速保持在100 r/min,钻头转速在0-200 r/min之间波动,粘滑现象非常严重。在这种情况下,基于钻柱均匀旋转的理论模型将不可行。
"粘滑运动"是一个物理学术语,通常用于描述物体在两个表面之间运动时的特性。它包括了两种主要类型的摩擦:
1.粘性摩擦(也称为动摩擦):这是指当两个物体之间相对运动时,由于它们之间的接触表面不是完全光滑的,所以会产生的摩擦力。这种摩擦力随着相对速度的增加而增加,但在某一点上会达到一个极限值,称为静摩擦系数。
2.滑动摩擦:这是指当一个物体相对于另一个物体开始运动时所产生的摩擦力。滑动摩擦力通常比静摩擦力小,一旦物体开始移动,滑动摩擦力会保持相对稳定。
这两种摩擦力可以用数学公式来描述,通常使用静摩擦系数(μs)和动摩擦系数(μk)来表示。 公式如下:
静摩擦力(Fs):Fs ≤ μs * N
其中,N是物体间的垂直压力或重力。
动摩擦力(Fk):Fk = μk * N
其中,N是物体间的垂直压力或重力。
理解粘滑运动对于设计和工程应用非常重要,因为它影响了许多日常物体和机器的性能。例如,汽车轮胎与路面之间的摩擦力决定了车辆的牵引力和制动效果。
首先分析了钻柱的运动,实际计算出在整个钻井过程中出现粘滑现象的频率。使用研制的旋转导向系统进行了多次现场试验,测量数据表明,在钻井过程中会频繁出现粘滑振动。
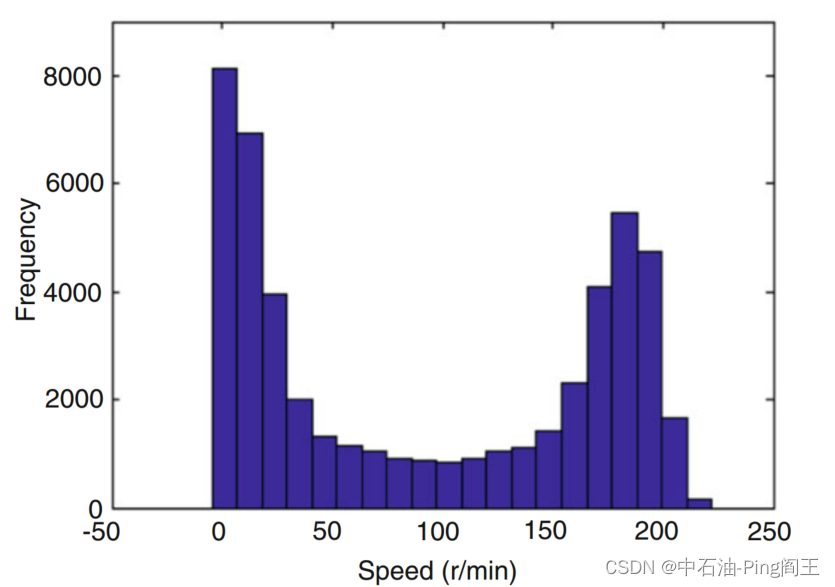
我们利用储层采样原理随机选取2 h的速度数据,根据样本的特征估计总体特征。 首先选取1 h的数据点顶部;假设有k个数据点;从第k + 1个数据点到达最后一个数据点;选择概率为1/i (i=k + 1, k + 2,…,N)的第i个数据点,并随机替换之前选择的一个元素。这个遍历时间可以保证1 h的数据点完全随机选择。如下图所示,接近于零的速度表示出现了粘滑。粘滑振动在钻井过程中始终存在,因此应用粘滑振动法提高测量精度是可行的。
1.1 实验数据
利用式(3.30)、式(3.31)和设计好的滤波器,建立DSP程序。将整个系统放到实验台上进行测量系统的精度测试。下图显示了加速度计(x、y、z轴)和磁通门(x、y、z轴)的测量数据。
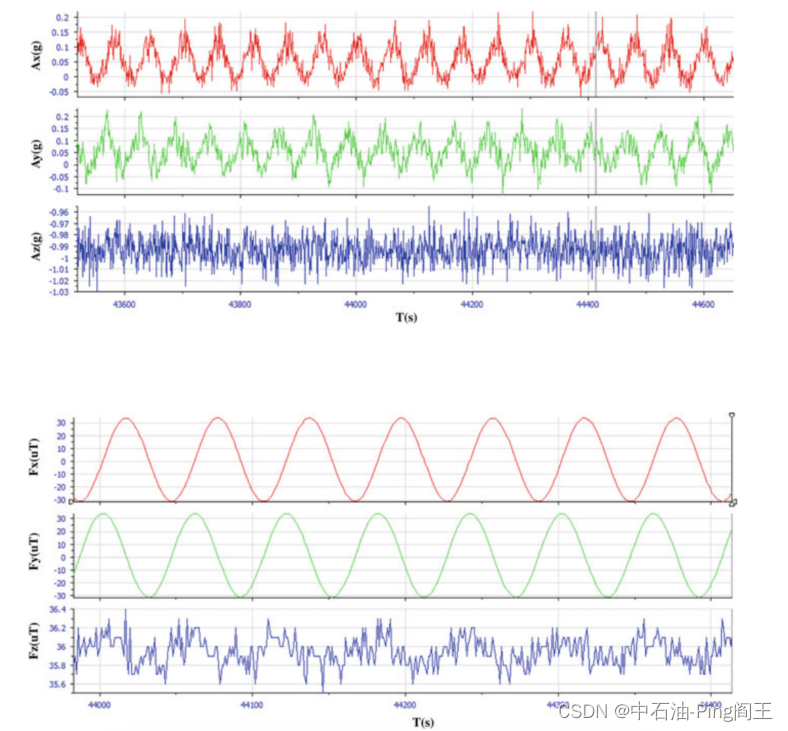
可以看出,加速度计的测量噪声相对大于磁通门;主要原因是加速度计对钻柱振动的敏感性。通过滤波可以得到一定程度上对噪声的消除。最后,试验中的倾角和方位角值如下图所示。其中X区为旋转钻柱振动噪声情况下的计算结果。
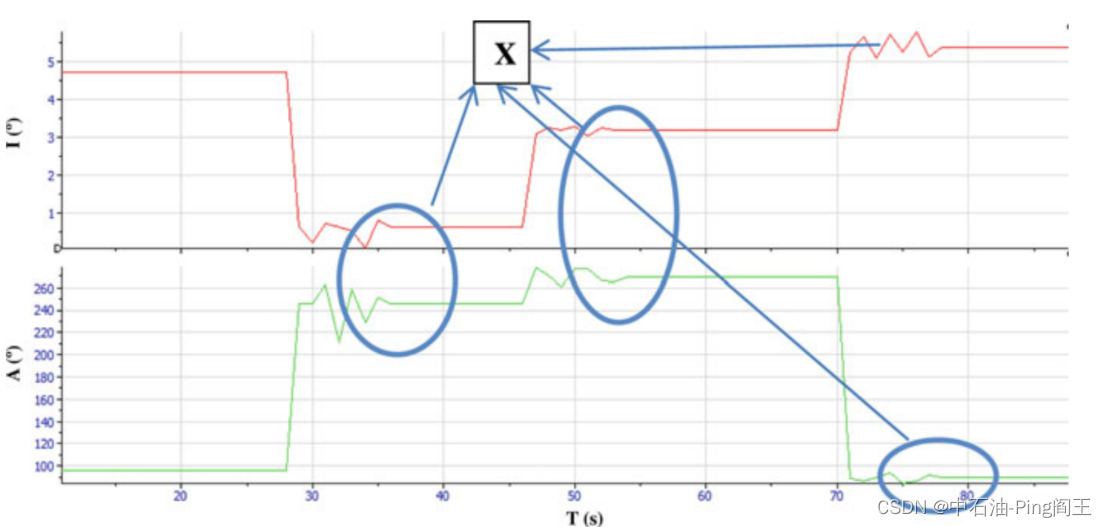
1.2 现场数据分析
在实际应用中,我们采用了低通滤波和移动平均滤波等方法,但在钻柱旋转时,效果并不理想。如下图所示,钻柱旋转时,倾角和方位角波动较大,而瞬时静止时,倾角和方位角波动明显较小,这促使我们寻求一种利用钻柱瞬时静止时数据的方法,以提高整个过程的精度。
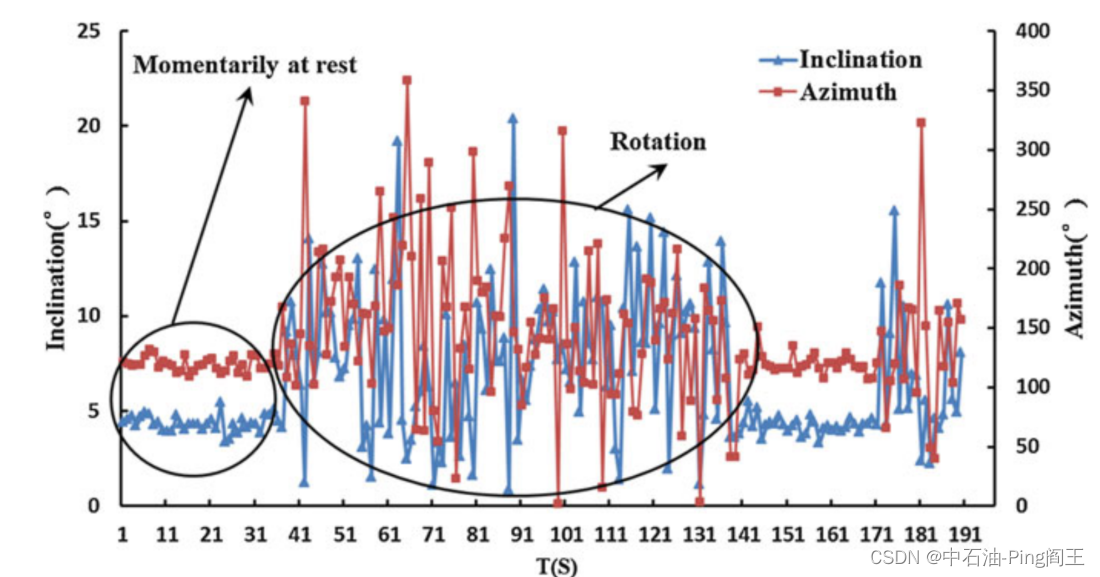
时间序列如上图所示,倾角和方位角每10 s计算一次,井下传感器采样频率为100 Hz。也就是说,每次计算使用1000个数据点,因此我们可以看到上图中的非旋转区域持续了大约400 s(论文中写的是400s,但是从图中我并没有看出持续了400s,有点像40s)。这是钻井过程中人为停止的结果。实际上,井下钻柱在地面似乎处于连续旋转状态时也会自动停止( 这就是粘滑运动带来的效果,其实说白了,就是一走一停的现象) 。
为了在更小的时间尺度上观察,如下图所示,采样频率为100 Hz, 500个数据点代表5秒。这些数据甚至不足以计算出上图中的一个点,但是我们找到了一个静止的区域,我们称之为粘性区域。在粘滞区,磁通门信号保持在固定值,加速度计信号有一定波动,但比钻柱旋转时的表现小得多。通过安装结构可以推断,y轴信号与x轴相似,相位相差90度°,所以图中没有显示y轴信号。
显然,在旋转时,加速度计信号也应该像磁通门信号一样呈现正弦波,但由于钻柱的强烈振动,我们没有看到这个结果。
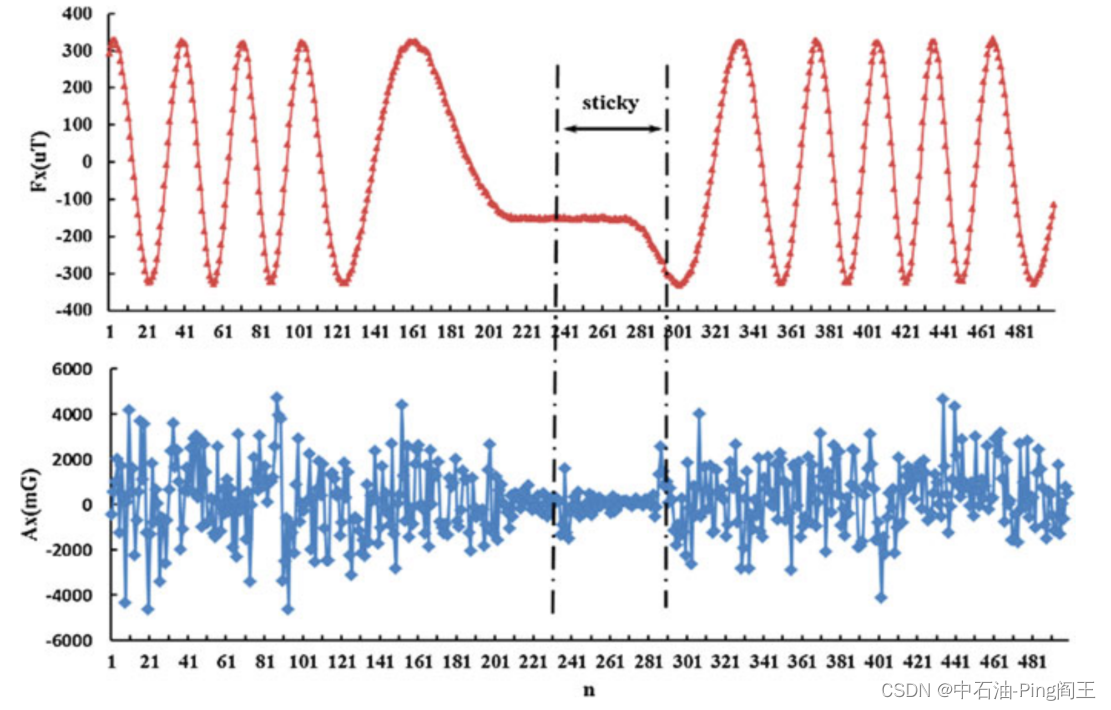
z轴加速度计信号也受到相对较小的振动的影响。我们使用移动平均滤波器进行进一步处理,如下式所示: A n = ∑ i = 1 10 a i A n + i − 9 , a i = 1 10 A_n = \sum_{i=1}^{10}a_iA_{n+i-9},a_i=\frac{1}{10} An=i=1∑10aiAn+i−9,ai=101
滤波后的信号得到了很大的改善,如图下图所示。在本章中,我们还使用FIR滤波器消除信噪比。对于磁通门信号,由于不受振动的影响,噪声信号被认为是高频分量。
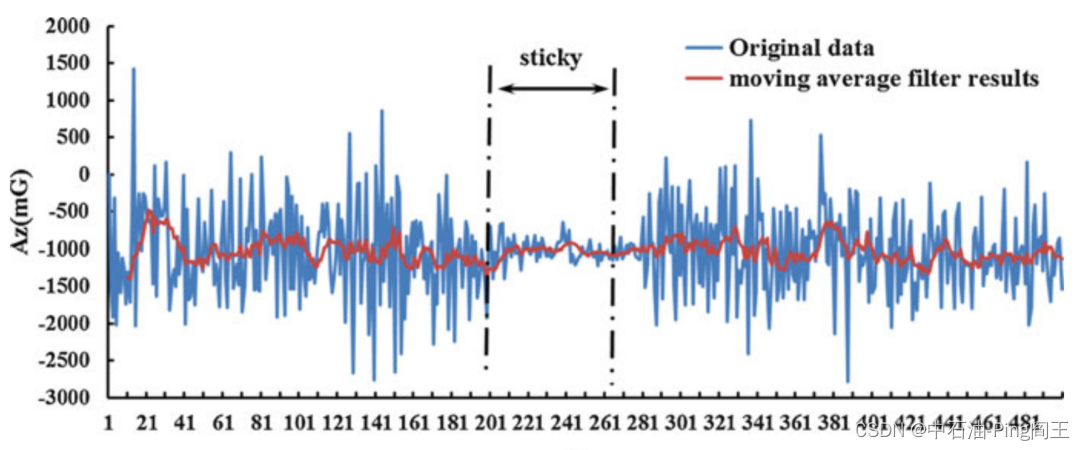
预处理后可进入动力计算部分。我们需要设置一个时间窗口来实时判断钻柱的运动状态。最大限度地利用隐藏在原始测量信号中的准确信息,提高最终的测量精度。
1.3 粘滑振动现象分析
首先要分析钻柱的运动,实际上是要 弄清楚在整个钻井过程中出现粘滑现象的频率。研制的旋转导向系统进行了多次现场试验,试验数据回放表明,粘滑振动的发生频率很高。由于数据量大,对整个测量数据进行分析既费时又费力。
因此,我们利用储层采样原理]随机选取2 h的速度数据,以便从样本的数据中估计总体特征。首先选择顶部1 h的数据点,假设有k个数据点,从第k + 1个数据点到最后一个数据点,选择第i个点的概率为 1 i \frac{1}{i} i1,并随机替换先前选择的元素。这个遍历时间得到1 h的数据点可以保证完全随机选择。
由下图可以看出,在零附近的速度表示出现了粘滑。粘滑振动在钻井过程中始终存在,因此应用粘滑振动法提高测量精度是可行的。
1.4 利用粘滑振动提高测量精度
1.4.1 粘滑振动的应用方法
下图提出了旋转钻柱底部姿态的动态求解方法,即在非旋转情况下,三轴实时信号滤波全部用于计算,同时存储x、y轴滤波信号;在旋转状态下,采用z轴实时滤波信号和非旋转管柱的x、y轴存储信号。
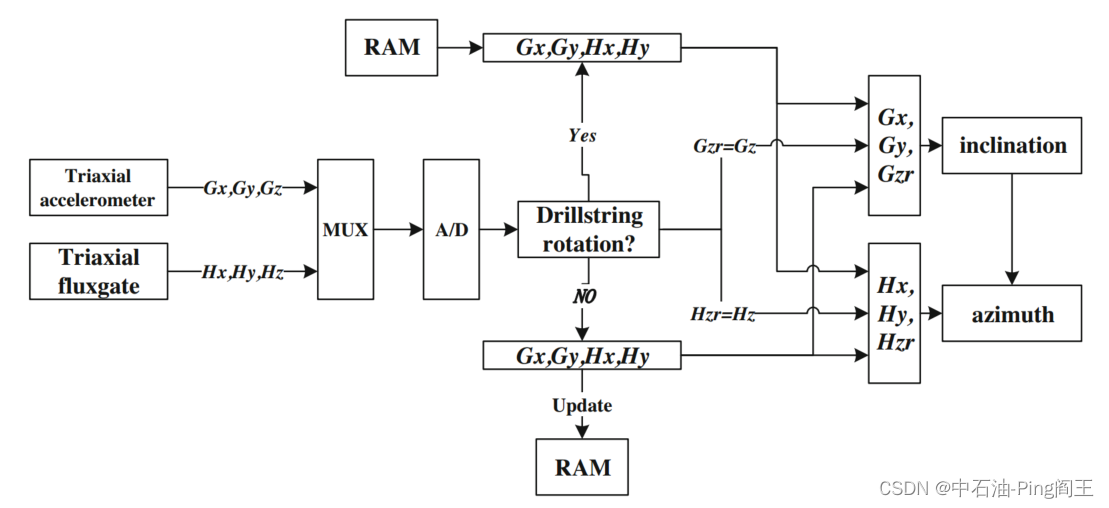
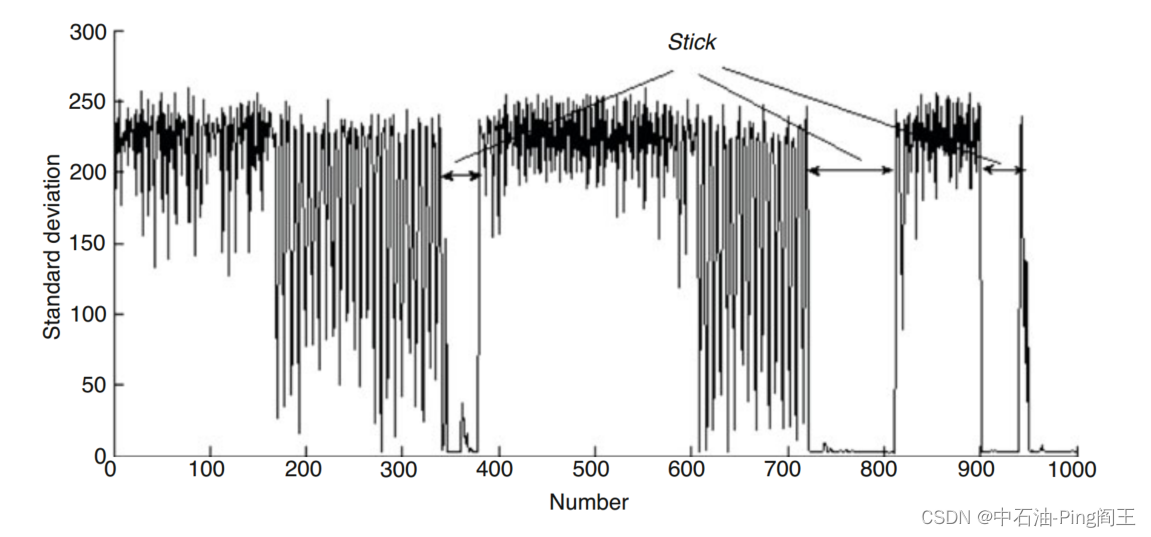
此外,井下钻具的粘滑状态被视为一种不旋转的“静止”状态。提出了基于井下实测数据的管柱旋转状态实时判断方法。钻柱转速可用于判断钻柱是否旋转,是一种切实可行的方法,但可靠性不高。通过以上分析,用标准差统计方法来确定钻柱运动将会更好,因为它反映了组内个体之间的分散程度。使用50个数据点作为时间窗口,假设为x1, x2,…, x49, x50,将得到标准差σ。如下图所示,当标准差接近于零时,钻柱力矩可以认为是静态的。
1.4.2 卡尔曼滤波
卡尔曼滤波是一种最优递归数据处理算法。它是最优的,因为它使用所有可用的信息来最小化给定系统状态变量中的错误。它是递归的,因为它不需要将所有以前的数据保存在存储中。它也是一种数据处理算法,因为它不是电滤波器,而是计算机程序。为了实现离散卡尔曼滤波器,误差模型必须以状态空间形式给出: x k = F k , k − 1 + G k − 1 w k − 1 ( 3.93 ) x_k = F_{k,k-1}+G_{k-1}w_{k-1} (3.93) xk=Fk,k−1+Gk−1wk−1(3.93) y k = H k x k + v k ( 3.94 ) y_k=H_kx_k+v_k(3.94) yk=Hkxk+vk(3.94)
式(3.93)称为动力学方程,式(3.94)为观测或更新方程。这里 x k x_k xk是过程状态向量, F k , k − 1 F_{k,k-1} Fk,k−1是 x k {x_k} xk与 x k − 1 x_{k-1} xk−1之间的方阵,称为状态转移矩阵,而 w k − 1 w_{k-1} wk−1是一个随机函数,以 G k − 1 {G_{k-1}} Gk−1为系数向量,被认为是白噪声。在式(12)中, y k {y_k} yk为第k时刻的测量向量, H k {H_k} Hk为给出观测向量与状态向量之间理想无噪声关系的设计矩阵, v k {v_k} vk为观测随机噪声。假设 v k {v_k} vk与 w k − 1 {w_{k-1}} wk−1无关。
定义刀具面为φ,倾角为θ,方位为ψ。变换矩阵Rn b可以定义为:
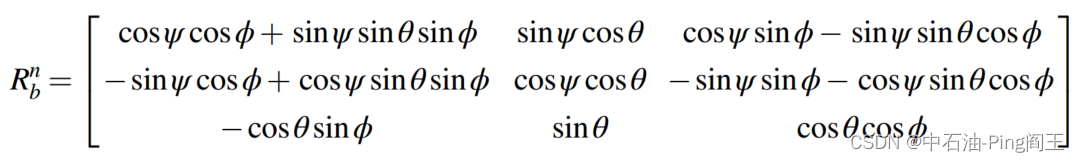
设 G b = [ G x G y G y ] T G^b=\begin{bmatrix}G_x &G_y &G_y\end{bmatrix}^T Gb=[GxGyGy]T,转速分别在xyz轴上定义为 w x , w y , w z w_x,w_y,w_z wx,wy,wz, w i b b = [ w x w y w y ] T w_{ib}^b=\begin{bmatrix}w_x &w_y &w_y\end{bmatrix}^T wibb=[wxwywy]T,则得到旋转角度。
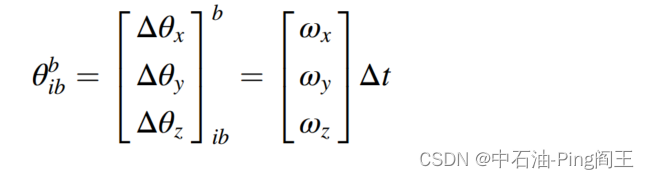
用四元数 Q = [ q 1 q 2 q 3 q 4 ] T Q=\begin{bmatrix}q1 &q2 &q3&q4\end{bmatrix}^T Q=[q1q2q3q4]T表示坐标系变换,则 R n b R_n^b Rnb可以重新定义为:
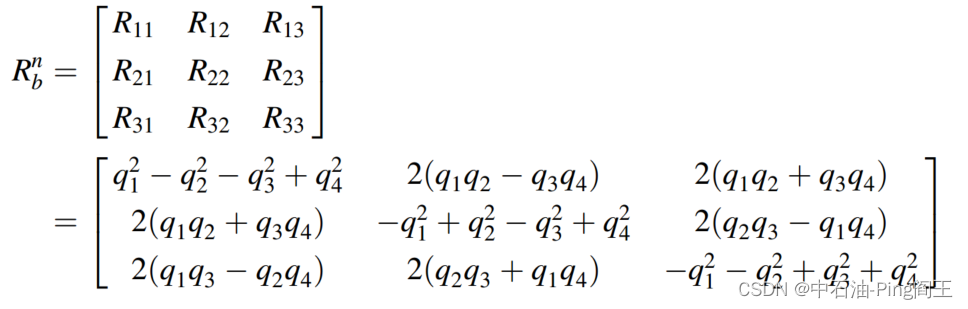
然后得到倾角和方位角求解的动力学方程:
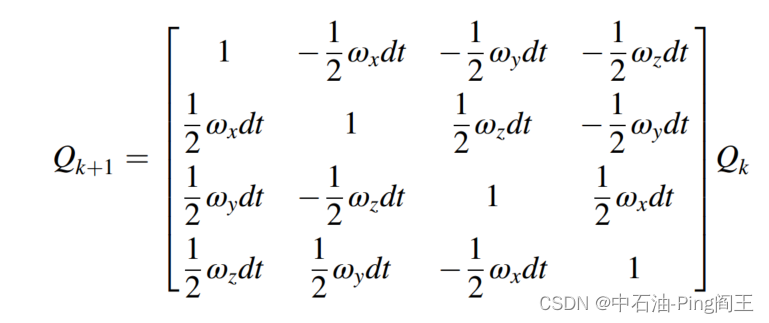
1.4.2 仿真效果
我们提取了旋转钻柱状态下的4000个数据点,Matlab仿真结果如下图所示。由此可见,利用粘滑现象,大大提高了钻柱动态旋转时的井眼倾角和方位角计算精度。
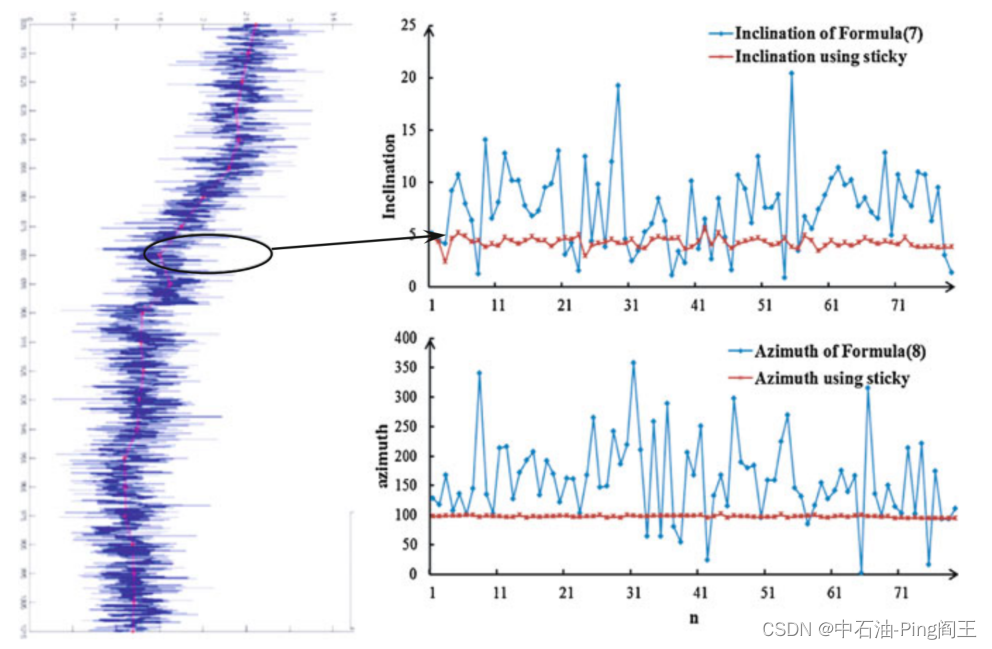
在定向钻井和旋转导向钻井技术及应用中,随着钻柱的旋转,如何实时准确测量井底钻具的空间姿态(倾角、方位、刀面)是一个具有挑战性的问题。仿真和实验表明,本章提出的动态求解方法能够满足工程要求。但钻柱的振动严重影响了动态求解的精度。通过对现场资料的统计分析,我们发现粘滑现象普遍存在,因此我们利用粘滑状态来开发一种动态算法,以提高井眼倾角和方位求解器的精度。仿真和实验评价结果表明,所设计的算法具有良好的实用性。这对定向钻井和旋转导向技术的发展具有参考意义。
二、 往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
相关文章:

课题学习(七)----粘滑运动的动态算法
一、 粘滑运动的动态算法 在实际钻井过程中,钻柱会出现扭振和粘滑现象(粘滑运动–B站视频连接),但并不总是呈现均匀旋转。如下图所示,提取一段地下数据时,转盘转速保持在100 r/min,钻头转速在0-…...

python二次开发CATIA:测量曲线长度
以下代码是使用Python语言通过win32com库来控制CATIA应用程序的一个示例。主要步骤包括创建一个新的Part文件,然后在其中创建一个新的几何图形集,并在这个集合中创建一个样条线。这个样条线是通过一组给定的坐标点来创建的,这些点被添加到集合…...
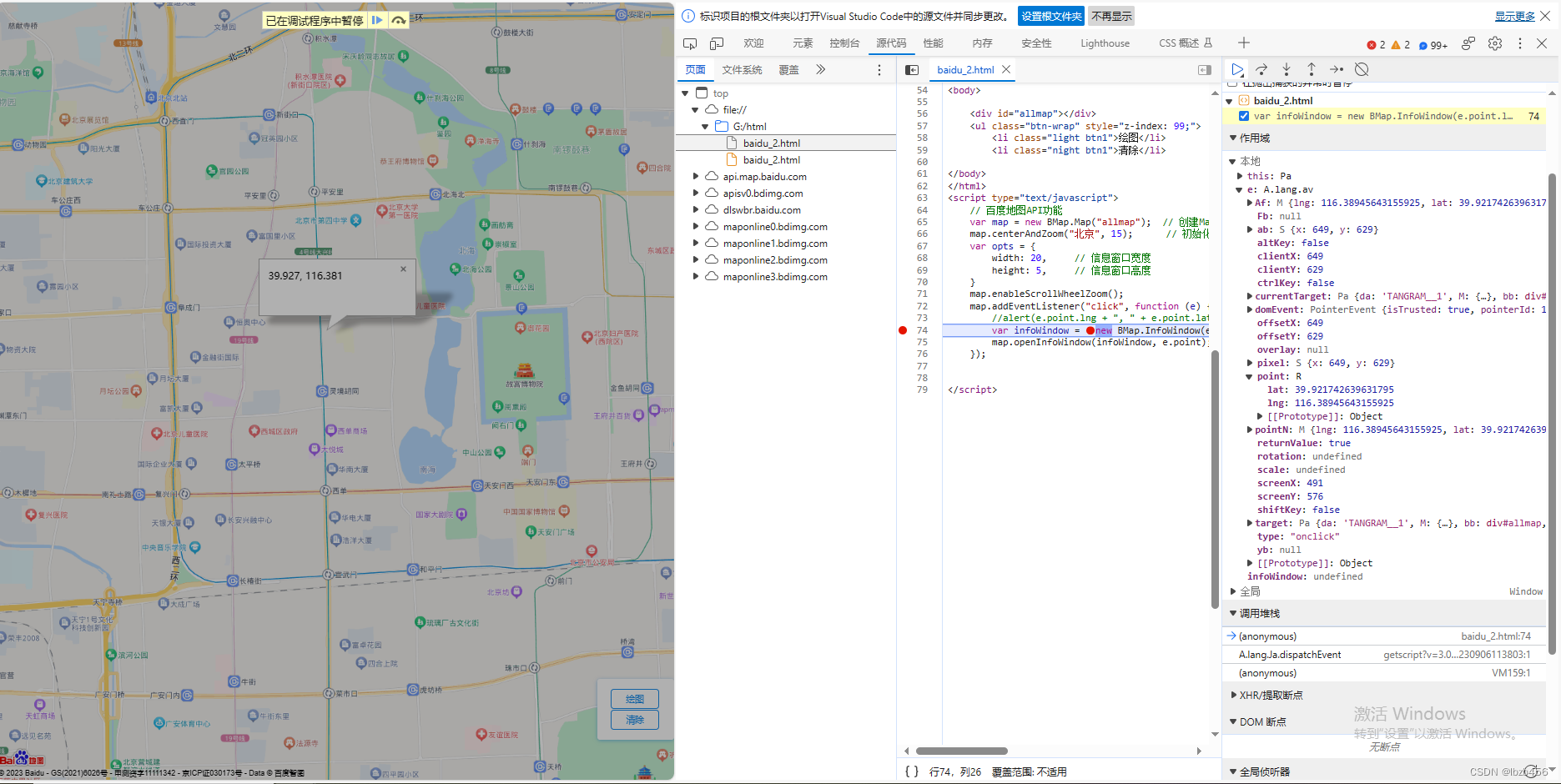
从零开始学习调用百度地图网页API:二、初始化地图,鼠标交互创建信息窗口
目录 代码结构headbodyscript 调试 代码 <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html; charsetutf-8" /><meta name"viewport" content"initial-scale1.0, user-scalable…...

Yarn基础入门
文章目录 一、Yarn资源调度器1、架构2、Yarn工作机制3、HDFS、YARN、MR关系4、作业提交之HDFS&MapReduce 二、Yarn调度器和调度算法1、先进先出调度器(FIFO)2、容量调度器(Capacity Scheduler)3、公平调度器(Fair …...

element picker 时间控件,指定区间和指定月份置灰
直接上代码 <el-date-pickerv-model"fillingList.declareDate"type"month":disabled"isDisplayName"placeholder"选择填报时间"value-format"yyyy-MM":picker-options"pickerOptions"change"declareDate…...

thinkphp6
unexpected , expecting case (T_CASE) or default (T_DEFAULT) or } 在模板中应用{switch}{/switch}标签,报错,其实是switch的问题,模板解析后,switch:和第一个case:之间不能有有输出的,一个空格也不行,所以第一个要紧跟着 Thi…...

Android 13.0 USB鼠标右键改成返回键的功能实现
1.概述 在13.0设备定制化开发中,产品有好几个usb口,用来可以连接外设,所以USB鼠标通过usb口来控制设备也是常见的问题,在window系统中,鼠标右键是返回键的功能,可是android原生的系统 鼠标右键不是返回键根据产品开发需要鼠标修改成右键就需要跟代码, 2.USB鼠标右键改…...

超低延时 TCP/UDP IP核
实现以太网协议集当中的ARP、ICMP、UDP以及TCP协议 一、概述 TCP_IP核是公司自主开发的使用FPGA逻辑搭建的用于10G以太网通信IP。该IP能够实现以太网协议集当中的ARP、ICMP、UDP以及TCP协议。支持连接10G/25G以太网PHY,组成高速网络通信系统。该IP上传、下传数据B…...

Python与数据库存储
Python与数据库存储的最佳实践包括以下几个方面的内容: 连接数据库:使用合适的数据库连接库,如sqlite3、psycopg2、pymysql等来连接数据库。创建连接对象并通过该对象获取游标。 import sqlite3# 连接SQLite数据库 conn sqlite3.connect(sam…...
及其使用)
RN操作SQLite数据库的包(sqlite-helper.js)及其使用
先安装 yarn add react-native-sqlite-storagesqlite-helper.js工具包的具体代码 "use strict";var _interopRequireDefaultrequire("babel/runtime/helpers/interopRequireDefault");Object.defineProperty(exports,"__esModule",{value:true…...
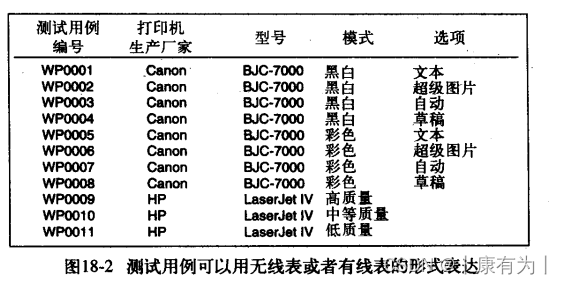
软件测试学习(四)自动测试和测试工具、缺陷轰炸、外包测试、计划测试工作、编写和跟踪测试用例
目录 自动测试和测试工具 工具和自动化的好处 测试工具 查看器和监视器 驱动程序 桩 压力和负载工具 干扰注入器和噪声发生器 分析工具 软件测试自动化 宏录制和回放 可编程的宏 完全可编程的自动测试工具 随机测试:猴子和大猩猩 使用测试工具和自动…...

【Rust日报】2023-10-12 论文:利用公共信息评估 Rust 代码库
论文 - 利用公共信息评估 Rust 代码库 作者 Emil Eriksson 是 Lund University 的硕士学生,今年春天发布了其硕士论文 Evaluation of Rust Codebases Using Public Information ,并获得了 electrical engineering 学位。 在论文撰写过程中,Em…...
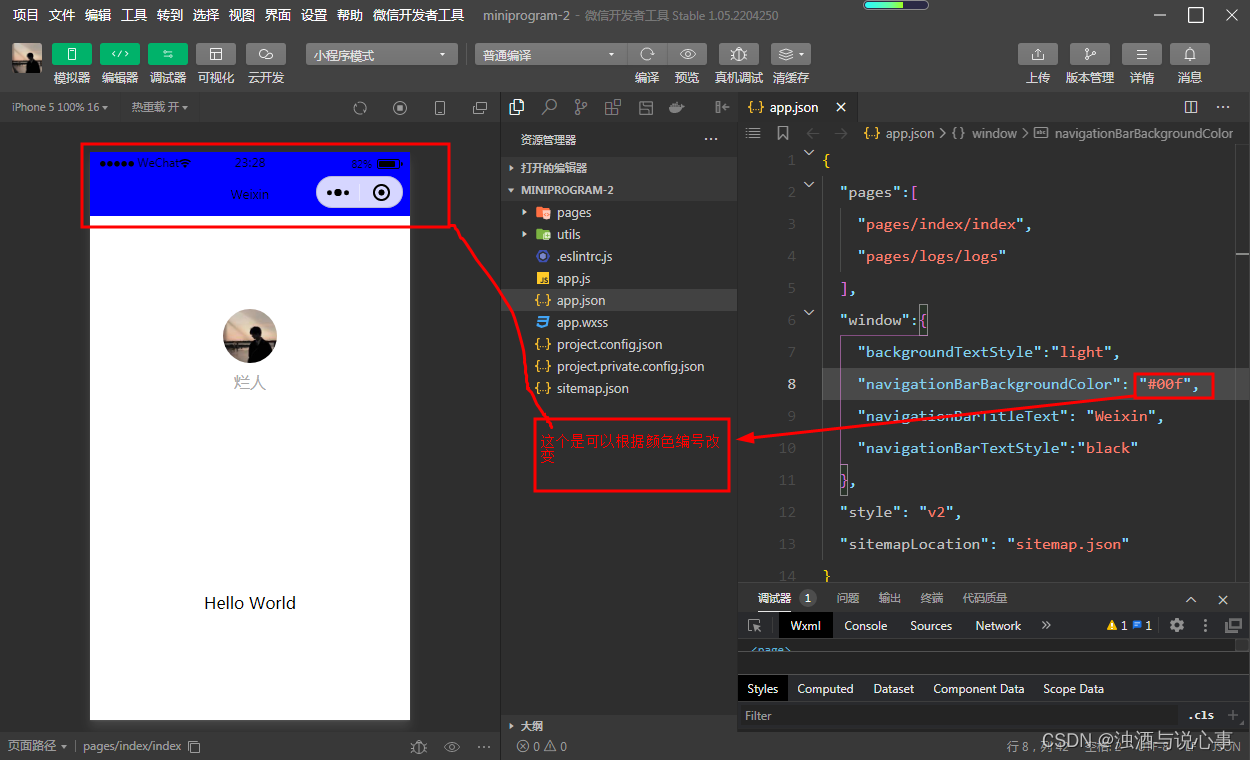
微信小程序入门
微信小程序介绍 微信小程序是一种轻量级应用程序,可以在微信中直接使用,无需下载和安装。它们基于微信的开发标准和API构建,并且可以实现许多不同的功能,例如娱乐、社交、购物、生活服务等。微信小程序用户仅需点击微信聊天窗口中…...
【RocketMQ系列二】通过docker部署单机RocketMQ
您好,我是码农飞哥(wei158556),感谢您阅读本文,欢迎一键三连哦。 💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精…...

中缀表达式转后缀表达式
58同城1012笔试第二题 示例1 输入 “exp1 & (exp2|exp3)/!exp4” 输出 “exp1 exp2 exp3| & exp4 !” 思路与代码 这个代码的核心思想是通过栈来处理不同操作符的优先级和括号的嵌套,将中缀表达式转换为后缀表达式,以便更容易进行计算。 …...

Zabbix 使用同一ODBC监控不同版本MySQL
一、ODBC介绍 ODBC是Open Database Connect 即开发数据库互连的简称,它是一个用于访问数据库的统一界面标准。ODBC引入一个公共接口以解决不同数据库潜在的不一致性,从而很好的保证了基于数据库系统的应用程序的相对独立性。ODBC 概念由 Microsoft 开发&…...
Swagger3.0 与spring boot2.7x 整合避免swagger2.0与boot2.7冲突
注释掉2.0引入的俩包 直接引入3.0 <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</version></dependency> swagger配置文件粘贴即用哦 import org.springfram…...

【HTML+REACT+ANTD 表格操作】处理(改变)数据,改变DOM
博主:_LJaXi 专栏: React | 前端框架 主要是一些表格DOM操作,数据更换 个人向 HTML <!DOCTYPE html> <html lang"en"> <link> <meta charset"UTF-8" /> <meta name"viewport" con…...

【面试经典150 | 哈希表】最长连续序列
文章目录 写在前面Tag题目来源题目解读解题思路方法一:哈希表 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内…...
如何构建安全的App网络通信?
前言 说到安全肯定逃不开数据的加解密,数据本地存储大多用对称加解密来实现,那网络传输数据的时候是不是也用对称加解密来实现?没错,常规网络通信时,大部分网络传输过程中基本也是用对称加解密来实现的,毕竟…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
