如何构建安全的App网络通信?
前言
说到安全肯定逃不开数据的加解密,数据本地存储大多用对称加解密来实现,那网络传输数据的时候是不是也用对称加解密来实现?没错,常规网络通信时,大部分网络传输过程中基本也是用对称加解密来实现的,毕竟时间宝贵。如果使用非对称加密方式,需要花N多时间等数据加密后传输出去,或者解密出来。只是用对称加解密有个致命问题就是密钥Key的交换,毕竟网络是一个不可靠加不安全的通信环境。这个时候就需要启用另外一种加解密方式——非对称加解密。
不过想要做出一个安全的加密通信信道不是简单的用个对称加密和非对称加密可以完成的。在说网络安全之前,我们先讲几个比较基础的概念。
1.1 单向函数
第一个要说的就是“单向函数”。假设现在存在一个函数,函数式为f(X)=Y。输入X,很容易就能得出结果Y。但是在知道结果Y,想反向算出输入值X时非常困难(就是用现有最快的计算机来计算,也得计算个几百上千年才能得出结果的这种)。这种函数就叫单向函数。其中最简单的就是整数相乘。例如3*7=21;知道21,很容易就能猜出来,可能的结果有【1,21】、【3、7】这两组。但是将整数的位数提高到几百位,就很难反推出来。
由此也能很容易的看出来单向函数不能用于数据加密。因为经过单向函数加密的数据谁都不能解开,用它来加密数据没有任何意义。单向函数一般两个用途:1、生成信息摘要,或者数据指纹。比如说我们非常熟悉的MD5、SHA1算法就是具有单向函数性质的摘要算法。2、密码保护。一般用户登录时给服务器提交明文密码是非常危险的,非常容易被抓包。就算千幸万苦的提交到服务器端,服务器端保存不当照样会造成用户密码泄漏。此时就需要将用户密码经单向函数计算,然后将计算出的函数值存储在服务器端。用户登录时,客户端只需要提交用户密码计算出的函数值,服务器端用接收到的函数值和本地存储的值进行对比即可。
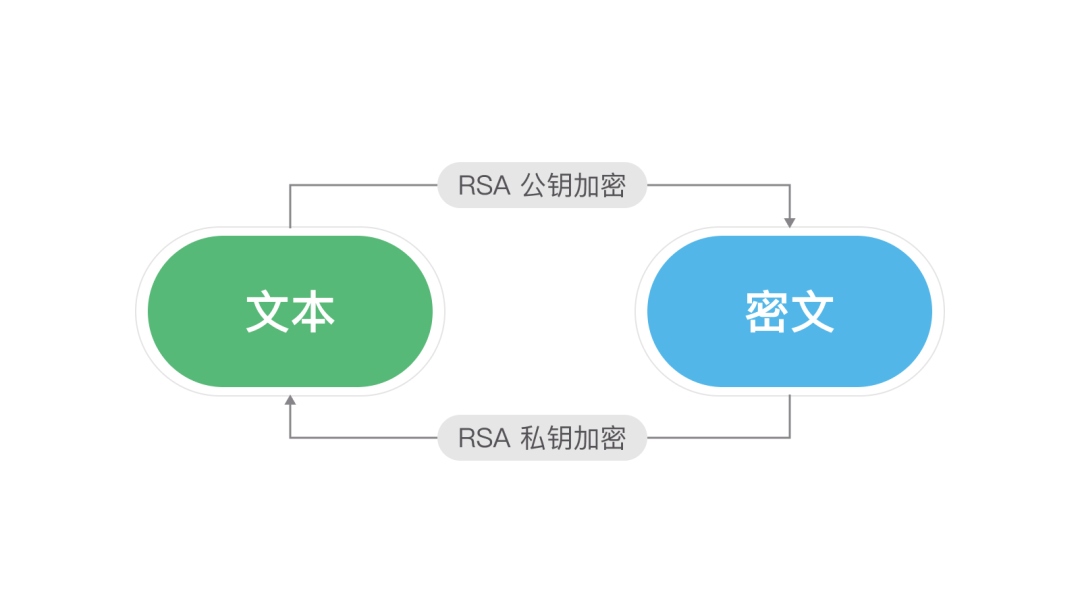
1.2 单向陷门函数
单向限门函数是一类特殊的单向函数。是一类存在“陷门”或者说“后门”的单向函数。还是上文提到的单向函数f(x)=y,已知函数计算方法和输入值x时非常容易计算得到结果y,但是反向不能计算。此时如果再提供一个参数、或者数据Z,就可以通过y反向计算出输入值X。这个Z就被称为后门或者说陷门。例如下图的利用RSA算法对数据进行加解密的过程中,私钥就可以被看做是“后门”。
1.3 前向加密安全
这个概念说的是:在一个加密通信信道中,用来产生会话的长期加密密钥泄漏,不会造成之前通讯密钥的泄漏。比如说在这个加密信道中发送了A、B、C、D、E五次网络请求,在第五次E的时候密钥被破解,第五次请求E被破译为明文。此时以后的请求G、H很难保证安全,但是之前的ABCD四次网络请求仍然无法被破译,还是安全的。
1.4 非对称加密
非对称加密算法有两个密钥,因为加密解密用的不同的密钥,所以就叫非对称加密。两个密钥,一个公布出去叫公钥,一个自己保留叫私钥。用公钥加密的数据,只有对应的私钥可以解密。用私钥加密的数据,也只有对应的公钥才可以解密。下图就是一个典型的公钥加密,私钥解密的过程。
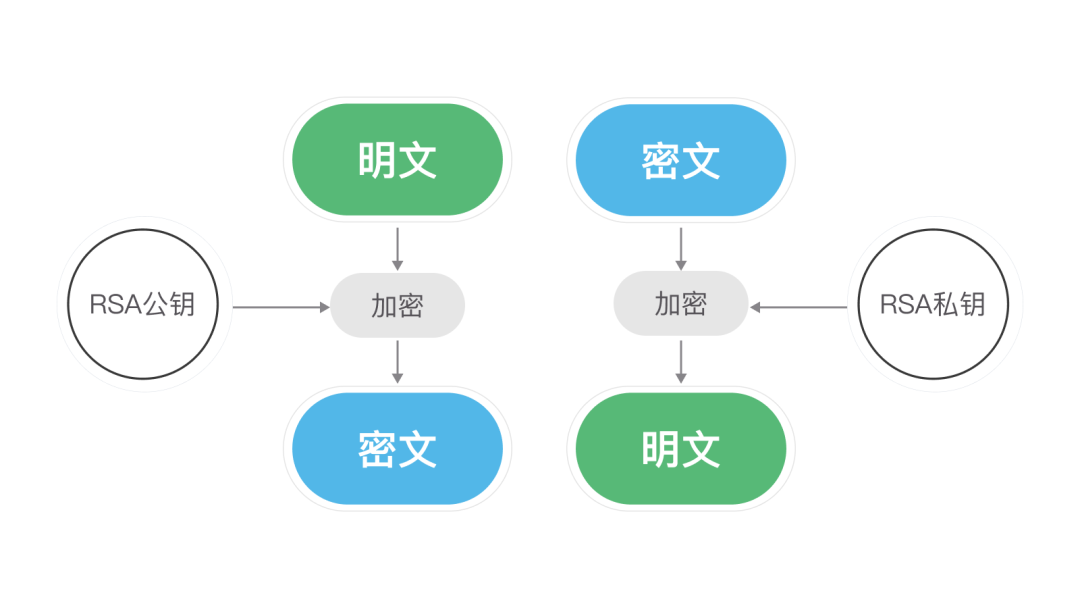
非对称加密算法有很多种,除了经常听说的RSA,还有D-H,ECC(椭圆曲线加密算法)等等算法。
网络安全通信
2.1 安全通信第一版
了解了非对称加密算法,我们很自然地就能设计出一个两端通信的安全加密方案。如下图所示:
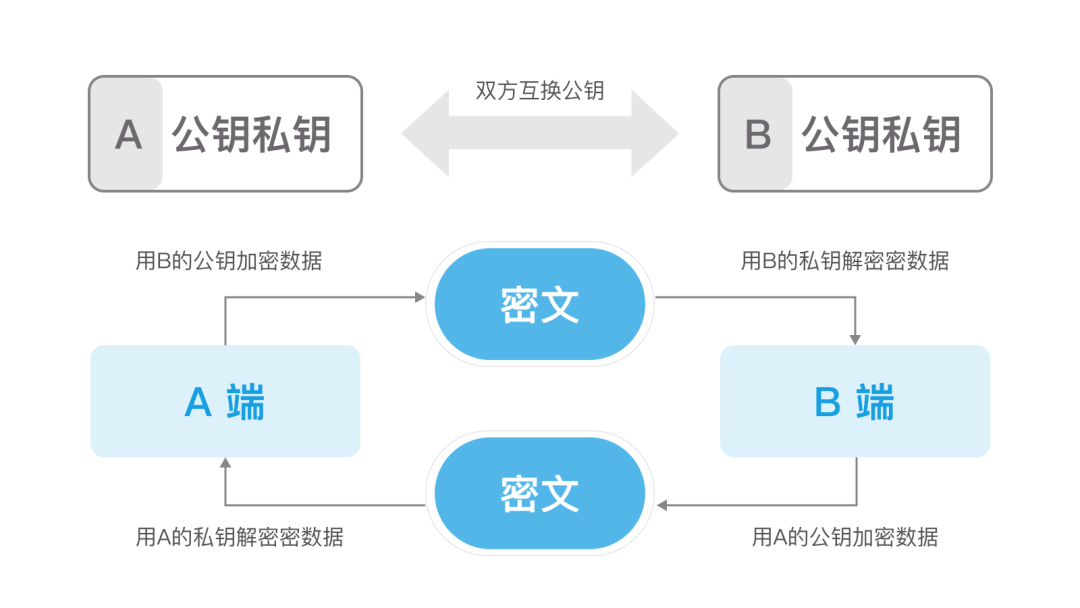
上述方案看似安全和完美,但是也存在一些问题和缺陷。比如性能差,会受到中间人攻击。
2.2 安全通信升级版
针对性能差,我们可以采用对称加密来解决。中间人攻击,这个时候就需要用到“数字证书”。数字证书的构成内容比较多,包含颁发者、使用者(持有者)、有效期、公钥等等。这里只说几个简单的知识点。
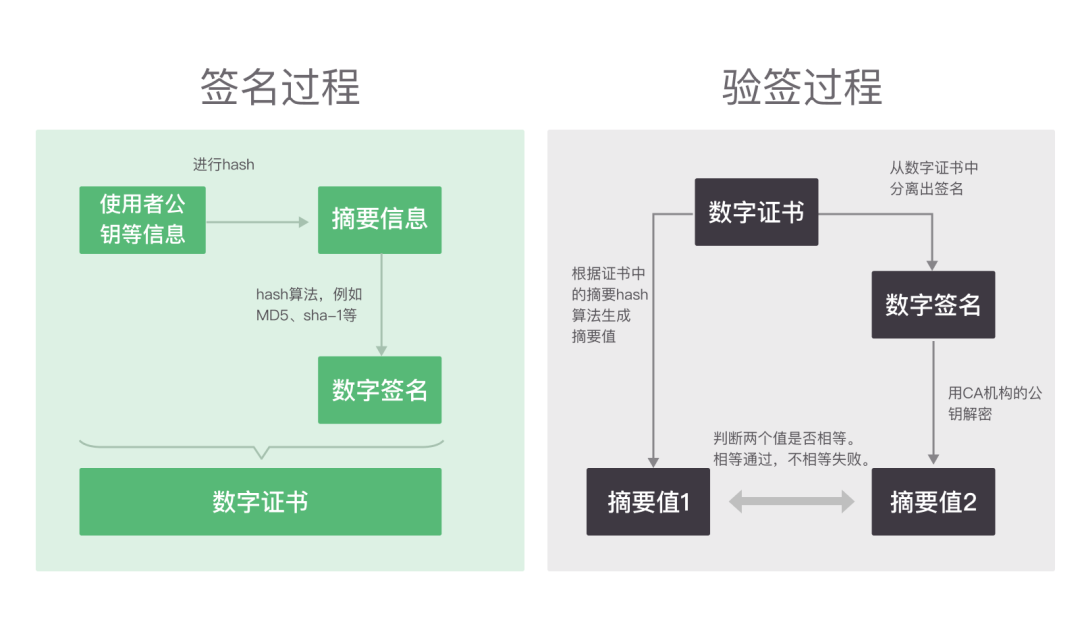
2.2.1 摘要
将使用者信息(这一栏一般是自身的网站域名和公司名等),自己生成的公钥和其他信息打包一起,经过hash算法计算,生成的hash值就叫做摘要。
2.2.2 签名
CA证书机构用自己的私钥对摘要进行加密运算,生成加密后的密文,这个密文就被称为是数字签名。
2.2.3 证书
将2.2.1中的自身信息和摘要,2.2.2步骤中的数字签名放在一起,就称之为数字证书。
下图就是一个签名生成数字证书和验证数字证书是否正确的流程图:
2.2.4 经典的TLS握手过程
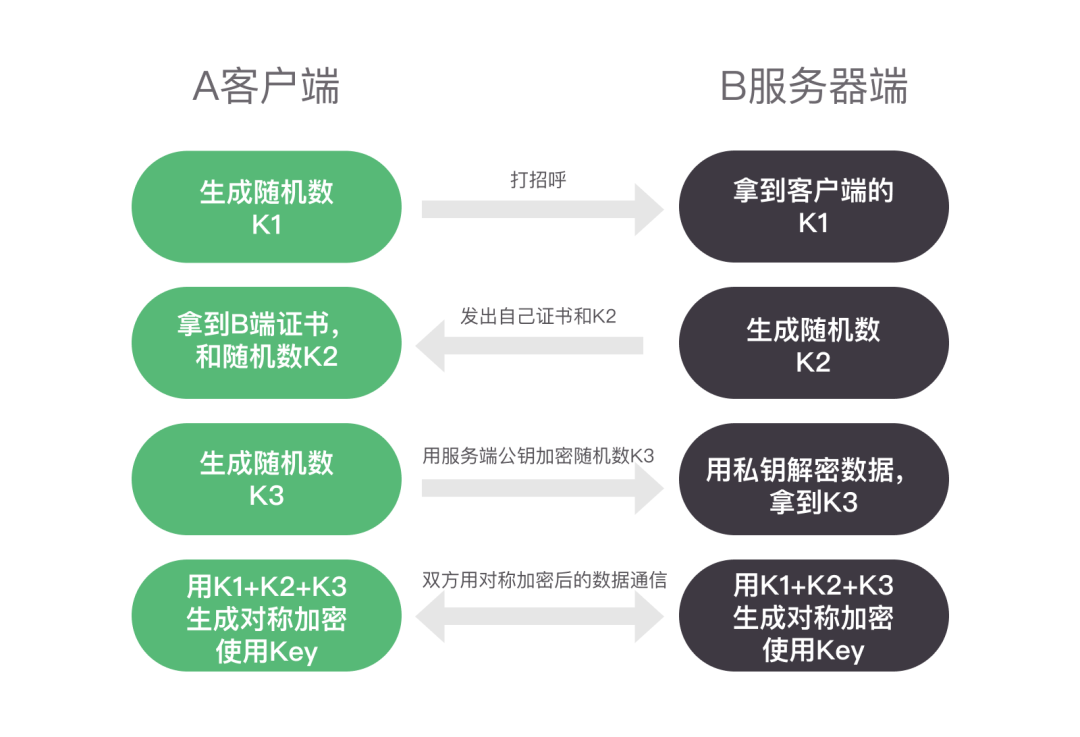
有了数字证书,再加上对称加密算法,我们就可以构建出一个安全的加密通信信道。
-
1. 首先客户端生成一个随机数k1,然后和服务器端打招呼并将随机数K1发送给服务器端。
-
2. 服务器端拿到K1。自己再生成随机数K2。并且将自身的证书和K2发送给客户端。
-
3. 客户端拿到服务器端的随机数K2和证书后,校验证书是否正确。如果校验成功,那继续进行握手。如果失败,会直接终止。
-
4. 客户端生成随机数K3,使用从证书中得到的服务器端公钥对K3进行加密。
-
5. 服务器端接收数据后,用自己的私钥对其进行解密,从而得到随机数K3。
-
6. 两端用三个相同的随机数K1+K2+K3合并生成一个对称加密算法的Key。后续就用这个key来加密两端通信的数据。
网络通信安全在众安APP中的落地
3.1 我们面对的严苛问题
看完上面安全知识点介绍和两种网络通信安全方案,我们就明白想构建一个安全的网络通信环境是多么的困难。尤其是我们做的金融App,那相对于普通APP安全等级更是严苛。
首先,金融APP不能只是简单的走Https协议而不做证书绑定校验(不做证书检验就会导致”中间人“攻击);
第二,App的网络请求需要配合服务器端做”防重放“处理,防止被人”重放攻击”;
第三,网络请求必须做签名处理,并且签名算法要保密,防止网络请求被篡改;
第四,网络请求数据必须做明文隐藏,防止网络请求被抓包的时候数据被攻击方直接获取;
第五,也是大家比较容易忽视的一点,就是多平台覆盖。很多App都做了网络请求安全防护,协议设计上大多只能兼容ios和android两端,web端就被忽视掉了;
第六,不能只顾安全不顾性能,App的网络通信性能必须兼顾到。
3.2 众安APP中的落地
所以我们需要一个全面、健壮、能兼顾到上面几个安全问题的方案。
参考TSL协议,相当于在Https请求的基础上再加一道防线,我们设计了众安的网络请求安全协议。
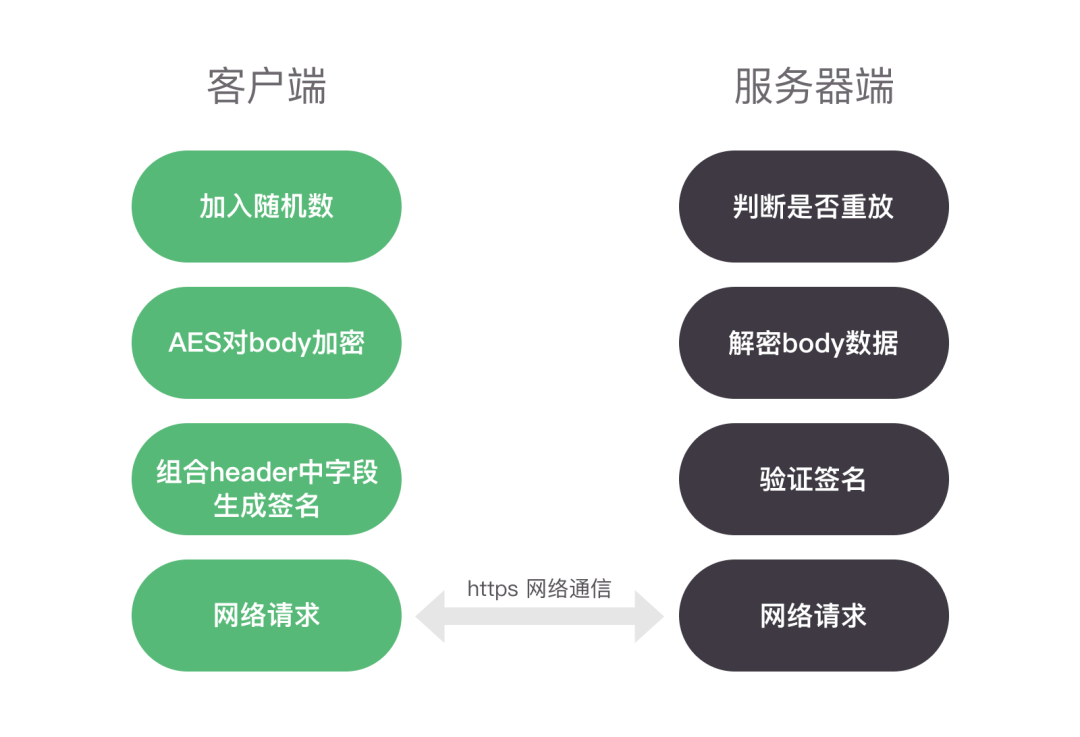
现详细说明一下该方案中的核心四步:
-
• 第一步自然就是采用https协议,挂上证书启用证书校验。此外由于SSL、TSL各个版本的缺陷,我们在服务器端写死了TSL 版本为1.2+。即发起请求的客户端TSL版本必须是1.2或者以上版本,否则在https的握手阶段网络连接就会失败。这一步旨在于有效的防止“中间人”攻击。
-
• 第二步,在每个网络请求的body中都放入一个随机数,后台服务器会在内存中记录这个随机数,并且加一个有效时间。这一步可以有效的防止”重放攻击“。
-
• 第三步,生成一对RSA的公私钥对。公钥放客户端,私钥放服务器端。每个网络请求使用随机算法生成一个随机数Key作为AES算法的key。用AES算法对网络请求的body数据整体进行加密。用公钥对key进行加密,加密后的值放到网络请求的head中。这一步是为了防止body明文泄密。
-
• 第四步,再次加固网络请求,给请求加签名——防篡改。使用header中的字段进行拼接,加入time这类随机数生成签名sign。这一步可以有效的防止网络请求被抓包后篡改。只要我们的签名算法没有泄漏或者被破解,那攻击者就很难篡改我们的网络请求。
下图就是一个完整的网络请求客户端发送,服务器端接收的过程。
其他的App网络通信方案介绍
再简单介绍两种密码登录交互方案供大家参考:
4.1 用户登录密码交互方案
大部分app都存在使用账号密码登录的情况。在这个时候为了保护用户的明文密码不泄漏,很多app就会采用下面这种或者类似方案来设计用户登录交互。

-
1. 首先在客户端对用户的明文密码附加盐值然后用hash算法计算生成密码。(这里之所以附加盐值后再hash是为了防止用户密码被人用彩虹表直接破译出来)
-
2. 服务器端准备两张表,当用户注册的时候,一张表用来存储用户提交的hash值密码,一个用来存储给用户生成的UUID随机码。(这里不存储用户明文密码就是为了防止服务器被脱库后,用户明文密码泄漏)
-
3. 用户登录的时候服务器端收到用户发来的hash密码,这里称为HashPW1,然后根据用户名查询到对应的UUID。服务器在自己的数据库中根据用户名查询出hash密码,称为HashPW2。接着查询到对应的UUID。
-
4. 然后在内存中用(HashPW1+UUID)生成密码1,用(HashPW2+UUID)生成密码2。两个密码相等即登录成功,不相等登录失败。(这里之所以在内存中生成真正的登录密码是为了防止将密码存储在数据库中,有权限的人可以直接查询到。经过这样复杂的操作有查询数据库权限的人只能看见两个hash值,不知道真正的密码如何生成。写代码的人知道密码生成算法,但是没有对应的随机值,都没有能力拿到用户的登录密码)
方案点评:
-
• 优点:该方案的最大优点在于隐藏客户的明文密码。整个系统的开发链上的几个关键角色:客户端开发、运维、后端开发都无法真正知晓客户的明文密码。在客户端,可以有效隐藏明文密码;在数据库中,存储的是客户的两个Hash值,运维无法掌握客户密码;在后端,虽然写后端代码的开发知晓真正的密码如何生成,但是却没有密码生成的两个关键hash值,仍然无法知晓客户的明文密码。
-
• 缺点:该方案缺点也是非常明显,客户端生成客户密码的hash值是固定的。如果被截取到该hash值就相当于被拦截了客户密码。必须在此基础上再加上网络通信安全策略,例如防抓包等策略,进一步加强防护。
4.2 用户交易密码交互方案
除了登录过程以外还有一种密码使用情况就是交易密码使用场景。理论上6位数字的交易密码也可以采用上面的交互方案,但是由于很多系统都对接了第三方系统,第三方系统只认用户的6位数字密码。也就是说我们还是需要将用户交易密码明文提交到服务器端。这时一般是这样操作的:

-
1. 第一步客户端通过API1发起请求到服务器。服务器端会有一个令牌池,令牌池中存储RSA公私钥对和一个随机码。收到用户请求后从令牌池捞出一对RSA公私钥对和随机码,和用户的token或者userId做绑定。
-
2. 第二步将绑定后的公私钥对中的公钥和随机码发送给客户端
-
3. 第三步客户端收到随机码和公钥后,将6位交易密码拼接随机码,整体用公钥加密生成密文串。客户端再通过API2提交密文串到服务器端。
-
4. 第四步,服务器端接收到密文串后,根据用户token或者userId查询到对应的私钥,用私钥解密得到对应的随机码和6位数字密码。随机码校验ok后即可使用交易密码;如果校验失败才用户本次无法使用交易密码。
方案点评:
-
• 优点:算是比较完美的方案,可以用于生产环境
-
• 缺点:系统的后端开发可以拿到用户的明文密码,如果操作不当,有密码泄露的风险。
总结
对于一个网络App来说,在一个不安全的网络环境中构建一条安全、稳定的网络通信信道非常重要,尤其对于金融App来说更是重中之重。简单地使用https协议并不能解决各种安全漏洞和网络攻击。综上所述,众安在构建自己的网络通信安全信道时进行了全方位的考虑:
-
• 在使用https协议的基础上,进行二次加密安全。即使https协议被破解,攻击者也只能获取到一堆加密过的密文信息。
-
• 网络请求不仅实现了“防篡改”和“防重放”,还采用了“前向加密安全”。每个请求的加密密钥都是独立且动态生成的。即使某一条请求被抓包和破解,也不会影响其他请求的安全性。
-
• 考虑多平台,该安全协议适用于iOS、Android和Web端。
-
• 在设计通信安全的同时,也考虑了与性能的平衡。不仅注重安全性,还优化了通信的性能,确保用户在使用ZA App时能够享受到快速、高效的网络通信体验。
附录
D-H算法
D-H算法全称Diffie-Hellman算法。是一种密钥协商算法,用来在不安全的网络环境中协商出一个统一的加密密钥。但是该方法不能防止中间人攻击。
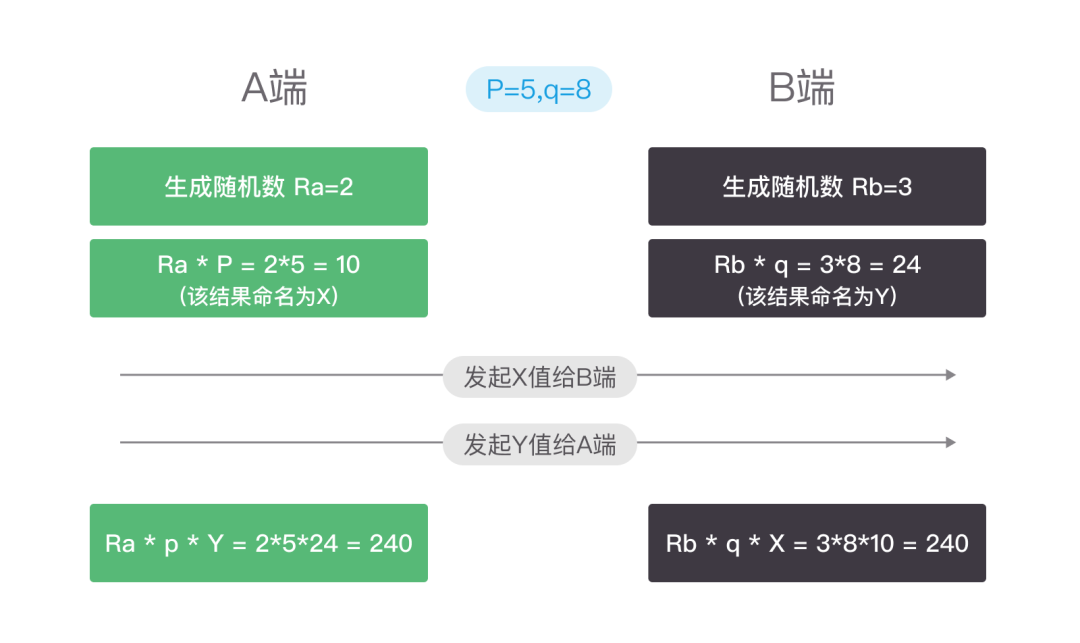
具体的密钥协商过程可以用下面这个交互过程简单理解一下。
-
• 首先A端和B端公开两个数字P和Q,其中P=5,Q=8。A端和B端各自生成一个随机数Ra=2、Rb=3。并且保证各自会保存好各自的随机码不泄漏。
-
• 接着A端采用公式Ra*P 计算结果X(X=10),B端采用公式Rb * Q 计算结果Y(Y=24)
-
• 双方互换X和Y值。这样A端拿到有Ra,P,Q,Y。B端持有Rb,P,Q,X。
-
• A端采用公式 Ra * P * Y 计算密钥,结果等于240。B端采用公式Rb * Q * X = 240。双方通过协商生成了统一的密钥240。
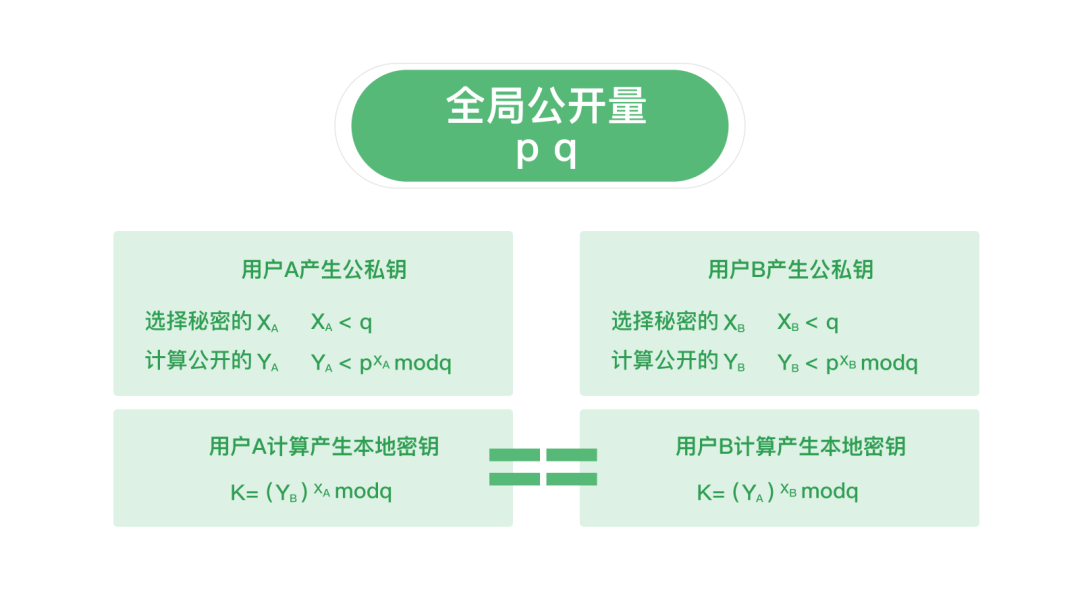
上面这个过程只是用乘法简单的模拟一下这个过程,具体的D-H算法要复杂的多,而且是采用离散对数来实现的。具体数学原理如下图所示:
本文作者: 谢鹏飞 来自于众安国际ZA Frontend 团队
相关文章:

如何构建安全的App网络通信?
前言 说到安全肯定逃不开数据的加解密,数据本地存储大多用对称加解密来实现,那网络传输数据的时候是不是也用对称加解密来实现?没错,常规网络通信时,大部分网络传输过程中基本也是用对称加解密来实现的,毕竟…...
Chrome插件精选 — 网页截图插件
Chrome实现同一功能的插件往往有多款产品,逐一去安装试用耗时又费力,在此为某一类型插件记录下比较好用的一款或几款,便于节省尝试的时间和精力。 捕捉网页截图 - FireShot 下载地址 (访问密码: 8276) Fireshot是一款浏览器插件,…...

react+antd封装表格组件2.0
reactantd封装表格组件2.0 1.0版本 仅仅封装组件,不涉及方法需要掌握知识点useImperativeHandle 组件代码引用 1.0版本 仅仅封装组件,不涉及方法 1.0 仅封装组件 此方法把所用方法集体封装,以后就可以无脑开发拉! 只需传入路径&…...

互联网Java工程师面试题·Java 并发编程篇·第八弹
目录 33、Java 死锁以及如何避免? 34、死锁的原因 35、怎么唤醒一个阻塞的线程 36、不可变对象对多线程有什么帮助 37、什么是多线程的上下文切换 38、如果你提交任务时,线程池队列已满,这时会发生什么这里区分一下: 39、J…...
21面向对象描述器
目录 1、什么是描述器? 1、原始的代码可以理解成为这样: 2、增加解释器可以改成如下,解释器就是集增删改查为一体的一个小的property 有一点需要注意的地方是:property里面内置的参数不是get_age()就是不用调用。 3、装饰器可…...

高校教务系统登录页面JS分析——皖西学院
高校教务系统密码加密逻辑及JS逆向 本文将介绍皖西学院教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习,勿用于非法用途。 一、密…...

单片机综合小项目
一、单片机做项目常识 1.行业常识 2.方案选型 3.此项目定位和思路 二、单片机的小项目介绍 1.项目名称:基于51单片机的温度报警器 (1)主控:stc51; (2)编程语言:C语言 (…...
)
docker下的onlyoffice安装(for seafile)
docker镜像拉取 # 拉取 onlyoffice 镜像docker pull onlyoffice/documentserver 创建所需目录 # 创建几个目录 用于 onlyoffice 的数据卷cd /opt# 建议与 seafile 容器都放在 /opt 目录方便管理mkdir seafile-onlyofficecd seafile-onlyofficemkdir logmkdir datamkdir libmkd…...

1 两数之和
解题思路: \qquad 对每个数nums[i],仅需在数组中搜索target-nums[i]是否存在。 优化思路: \qquad 首先能想到,利用哈希表O(1)查询target-nums[i]。 \qquad 建立map<int, vector<int>>的表能够处理重复元素&#x…...
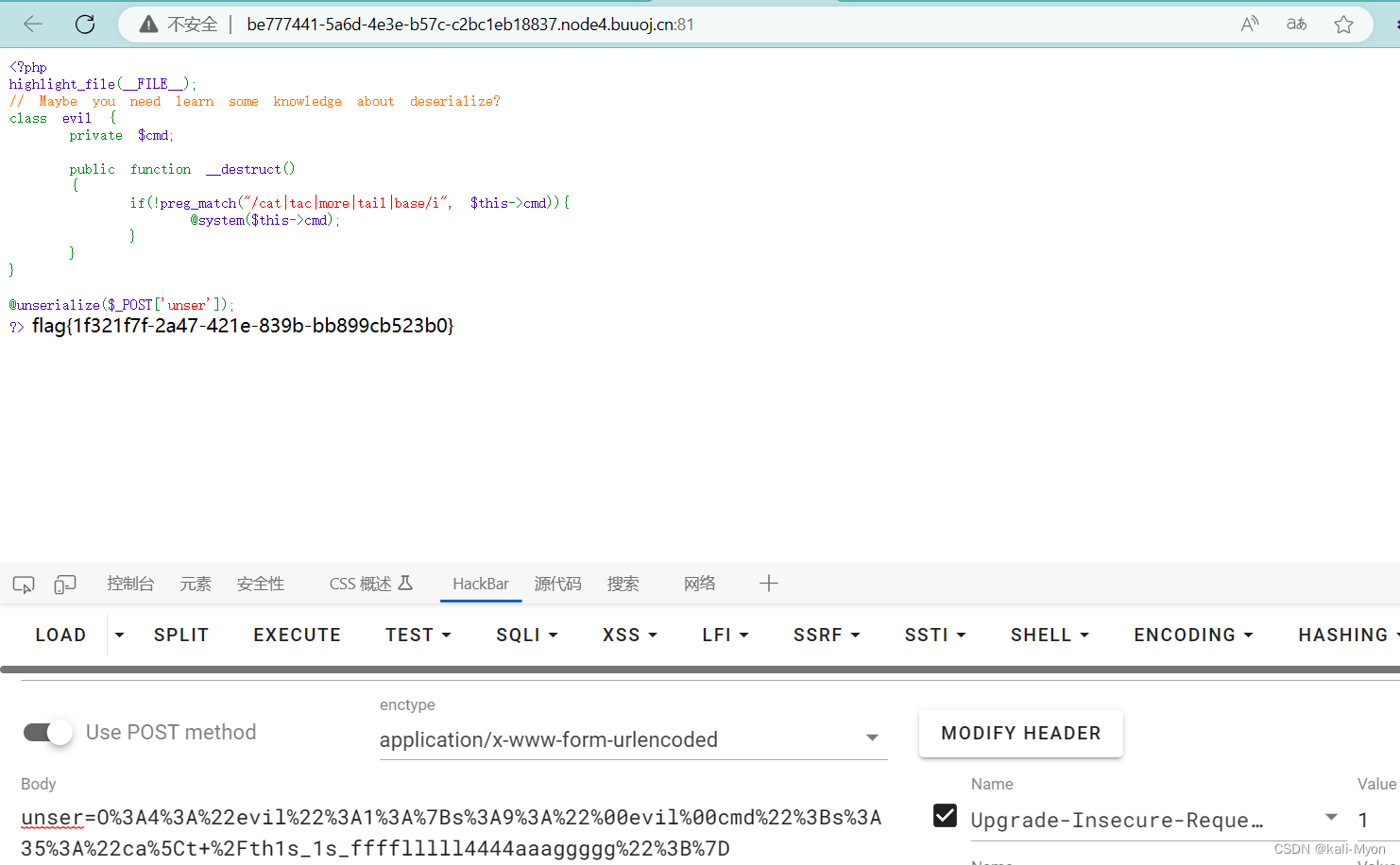
NewStarCTF2023week2-Unserialize?
代码审计: 定义了一个eval类,该类下有一个私有变量cmd和公有成员函数destruct(),该函数在对象的所有引用都被删除或类被销毁时会自动调用; 调用该函数则会执行一个正则表达式进行正则匹配,过滤掉了一些常用命令和bas…...

OpenMesh 最优选点策略
文章目录 一、简介二、实现代码三、实现效果参考文献一、简介 继续沿着之前的思路:OpenMesh 网格顶点Quadric误差计算,有时候,无论是网格简化或是网格平滑,总会涉及到添加一个新的顶点的问题,那么新顶点应该怎么生成呢?以网格的简化操作为例,假设我们要合并两个顶点,也…...

服务器内存总量和内存条有差异是什么问题 103.239.244.X
服务器内存总量和内存条上标注的容量可能会存在一些差异,这是由于以下几个原因: 部分内存被保留给系统和其他硬件设备:在服务器中,一部分内存可能被保留给系统和其他硬件设备,比如显卡、网卡、RAID卡等。这些设备需要一…...

WPF DataGrid详细列表手动显示与隐藏
设置显示序号与折叠显示样式 <DataTemplate x:Key"dtNum"><Button BorderBrush"Transparent" Style"{x:Null}" Click"BtnRowDetail_ShowHideClick" FontSize"16" Background"Transparent"><Stack…...
Compose 组件 - 分页器 HorizontalPager、VerticalPager
一、概念 类似于 ViewPager,1.4 版本之前需要借助 accompanis 库,底层基于 LazyColumn、LazyRow 实现,在使用上也基本相同。默认情况下 HorizontalPager 占据屏幕的整个宽度,VerticalPager 会占据整个高度。 fun HorizontalPager(…...

Web3 招聘 | Bitget、MyShell、imToken、Arweave 多项目招聘中
「Web3 招聘」是 TinTinLand 为 Web3 项目和求职者创建的一个招聘信息汇集专栏。本栏目将持续更新区块链行业招聘信息,满足不同求职者与项目方的多样需求。欢迎各项目方联系 TinTinLand 发布职位需求,欢迎求职者关注 TinTinLand 获取最新招聘信息。 此外…...

通过HTTP发送大量数据的三种方法
在网络的早期时期,人们发送的文件大小仅为几KB。到了2023年,我们享受着高分辨率的MB级别图像,并在几GB的4K(即将是8K)视频中观看。 即使有良好的互联网连接,下载一个5GB的文件仍然需要一些时间。如果你拥有…...

【MySQL】索引和事物
目录 ♫索引 ♪什么是索引 ♪索引的数据结构 ♪索引的使用 ♫事务 ♪什么是事务 ♪事务的特性 ♪事务的使用 ♫索引 ♪什么是索引 索引是存储在磁盘上的一个数据结构,通过索引可以快速地定位到存储在磁盘上的数据。 索引在提高查询速度的同时,还提…...
win11下的VS2022+QT6+VTK9.2+PCL1.13.1联合开发环境配置及踩坑记录
准备工作: 安装VS2022:这个比较简单,网上随便找个教程就行 安装QT并为VS2022添加QT Creater插件:VS2022配置Qt6_vs2022 qt6-CSDN博客 安装PCL:vs2022配置pcl1.13.1_pcl配置-CSDN博客 安装PCL过程中本身也会安装VTK&…...

CEdit
1、https://www.cnblogs.com/milanleon/p/5626174.html 2、CEdit控件提供访问函数主要有: int GetWindowText(LPCTSTR lpszStringBuf,intnMaxCount) 获取控件文本,与ReadText()功能相同 void SetWindowText(LPCTSTR lpszString) 设置控件文本 void …...

vue3 自定义指令
Vue 除了内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令。 一个自定义指令由一个包含类似组件生命周期钩子的对象来定义。钩子函数会接收到指令所绑定元素作为其参数。 在setup语法糖中,任何以 v 开头的驼峰式命名的变量…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...

【Axure高保真原型】图片列表添加和删除图片
今天和大家分享图片列表添加和删除图片的原型模板,效果包括: 点击图片列表的加号可以显示图片选择器,选择里面的图片; 选择图片后点击添加按钮,可以将该图片添加到图片列表; 鼠标移入图片列表的图片&…...
