当前位置： 首页 > news >正文

Mac下通过nvm管理node

news 2026/2/10 22:22:17

背景

本地有两个项目，老项目需要用到node 14，新项目需要用node 16，所以只能通过nvm来管理node了

卸载原始的node

我的node是通过官网的.pkg文件安装的，可以通过以下命令进行删除

sudo rm -rf /usr/local/{bin/{node,npm},lib/node_modules/npm,lib/node,share/man/*/node.*}

安装nvm

使用brew安装nvm非常简单，命令如下

brew install nvm

安装完成后，需要为nvm创建一个目录

mkdir ~/.nvm

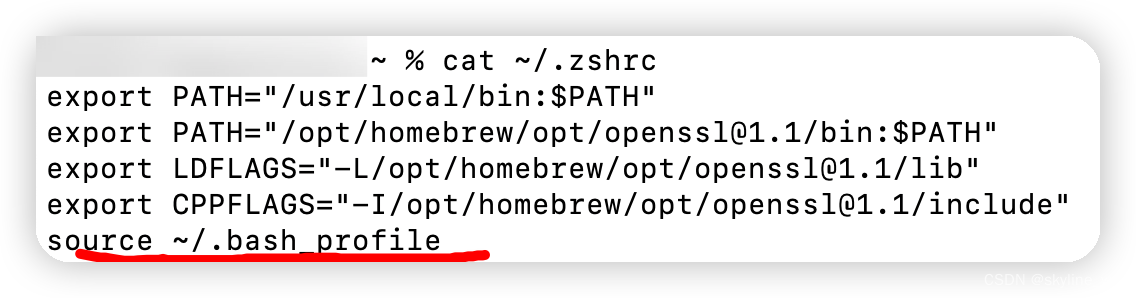
然后修改配置文件，可以修改~/.bash_profile也可以修改~/.zshrc，区别在于~/.bash_profile中的修改需要每次都source一下，但是~/.zshrc只要source一次就可以了。我这里修改的是~/.bash_profile

export NVM_DIR="$HOME/.nvm"[ -s "/opt/homebrew/opt/nvm/nvm.sh" ] && \. "/opt/homebrew/opt/nvm/nvm.sh"  # This loads nvm[ -s "/opt/homebrew/opt/nvm/etc/bash_completion.d/nvm" ] && \. "/opt/homebrew/opt/nvm/etc/bash_completion.d/nvm"  # This loads nvm bash_completion

修改完后，执行source ~/.bash_profile，此时就可以查看nvm的版本了
在这里插入图片描述
因为~/.bash_profile需要每次都source一下，所以可以把source ~/.bash_profile写到~/.zshrc中，这样每次直接打开终端就可以执行nvm命令了
在这里插入图片描述

安装node

可以通过nvm ls-remote命令来查看当前服务器上所有的node版本，比如我要安装node 16 直接执行下面的命令就行

nvm install 16

需要注意一下，第一次安装node，可能会有一个非常慢的make过程，安心等待即可
在这里插入图片描述

查看本地node版本

使用下面的命令可以查看本地的node版本

node ls

在这里插入图片描述

切换node版本

使用如下命令可以切换node版本

node use 14

在这里插入图片描述

注意事项

切换node时最好先关闭使用node的进程，不然可能出现各种奇怪的问题

相关文章：

Mac下通过nvm管理node

背景 本地有两个项目，老项目需要用到node 14，新项目需要用node 16，所以只能通过nvm来管理node了 卸载原始的node 我的node是通过官网的.pkg文件安装的，可以通过以下命令进行删除 sudo rm -rf /usr/local/{bin/{node,npm},lib/…...

编程日记 2023/10/15 12:19:25

易点易动固定资产管理系统：RFID出入监控，保障固定资产安全

在企业管理中，固定资产的安全和管理一直是一项重要的任务。企业往往面临着固定资产丢失、盗窃和不当使用等问题，给企业带来巨大的经济损失和管理难题。为了解决这些问题，我们推出了易点易动固定资产管理系统，结合RFID出入监控技术…...

编程日记 2023/10/15 12:18:23

Vue封装组件并发布到npm仓库

1. 环境准备 因为我们此次封装的是Vue组件，所以我们直接在Vue脚手架项目里面进行封装即可。 （1）初始化Vue项目 vue create lin-vue （2）运行项目 npm run serve 2. 组件封装 新建src/components文件夹 因为我们可…...

编程日记 2023/10/15 12:15:18

python+深度学习+opencv实现植物识别算法系统 计算机竞赛

0 前言 🔥 优质竞赛项目系列，今天要分享的是 🚩 基于深度学习的植物识别算法研究与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数：4分工作量：4分创新点：4分 🧿 更多…...

编程日记 2023/10/15 12:14:16

基于springboot实现医院急诊平台系统项目【项目源码】

基于springboot实现医院急诊平台系统演示 Spring Boot框架 Spring Boot是Pivotal团队的一个新框架，旨在简化新Spring应用程序的初始设置和开发。该框架使用特定的配置方法，无需开发人员定义样板配置。通过这种方式，Spring Boot旨在成为蓬勃发…...

编程日记 2023/10/15 12:13:15

【02】基础知识：React - jsx语法规则

一、jsx 简介 全称为JavaScript XML&#xff0c;是 react 定义的一种类似于 XML 的 JS 扩展语法 JS XML 本质是 React.createElement(component, props, …children) 方法的语法糖&#xff0c;用来简化创建虚拟 DOM 写法&#xff1a;var ele <h1>Hello JSX!</h1&…...

编程日记 2023/10/15 12:12:14

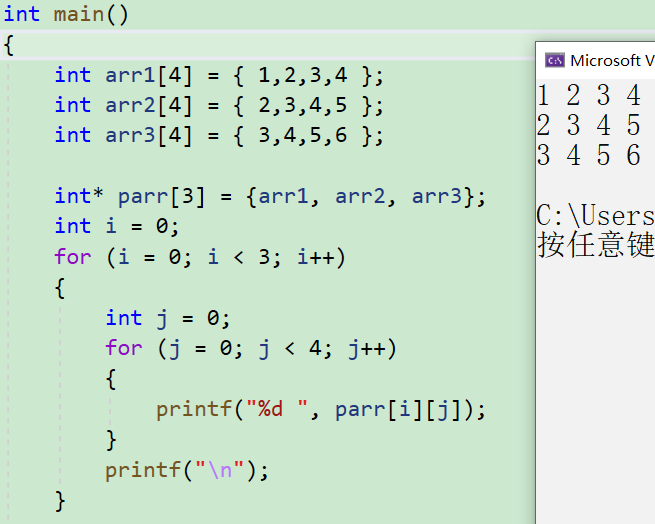
C语言 —— 指针

目录 1. 指针是什么&#xff1f; 2. 指针和指针类型的关系 2.1 指针的解引用 2.2 指针-整数 3. 野指针 3.1 野指针成因 1. 指针未初始化 2. 指针越界访问 3. 指针指向的空间释放 3.2 如何规避野指针 4. 指针运算 4.1 指针-整数 4.2 指针-指针 指针-指针的使用 4.3 指针的关系运…...

编程日记 2023/10/15 12:11:13

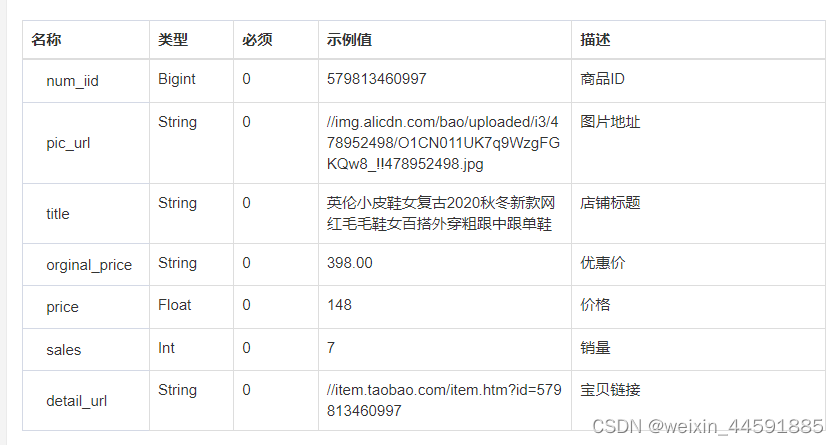
淘宝店铺所有商品数据接口，淘宝整店所有商品数据接口，淘宝店铺商品接口，淘宝API接口

淘宝店铺所有商品数据接口可以通过淘宝开放平台获取。以下是具体步骤&#xff1a; 在开放平台注册成为开发者并创建一个应用&#xff0c;获取到所需的 App Key 和 App Secret 等信息。使用获取到的 App Key 和 App Secret 进行签名和认证&#xff0c;获取 Access Token。调用开…...

编程日记 2023/10/15 12:10:12

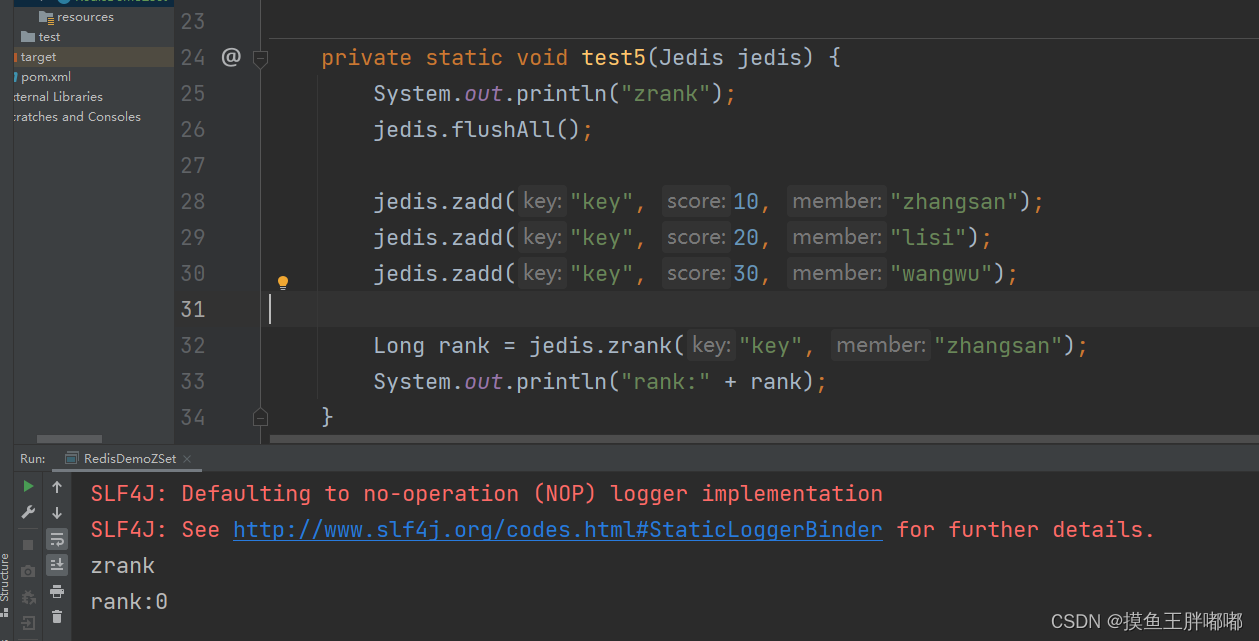
【Redis】Java客户端使用zset命令

zadd/zrange zcard zrem zscore zrank...

编程日记 2023/10/15 12:09:11

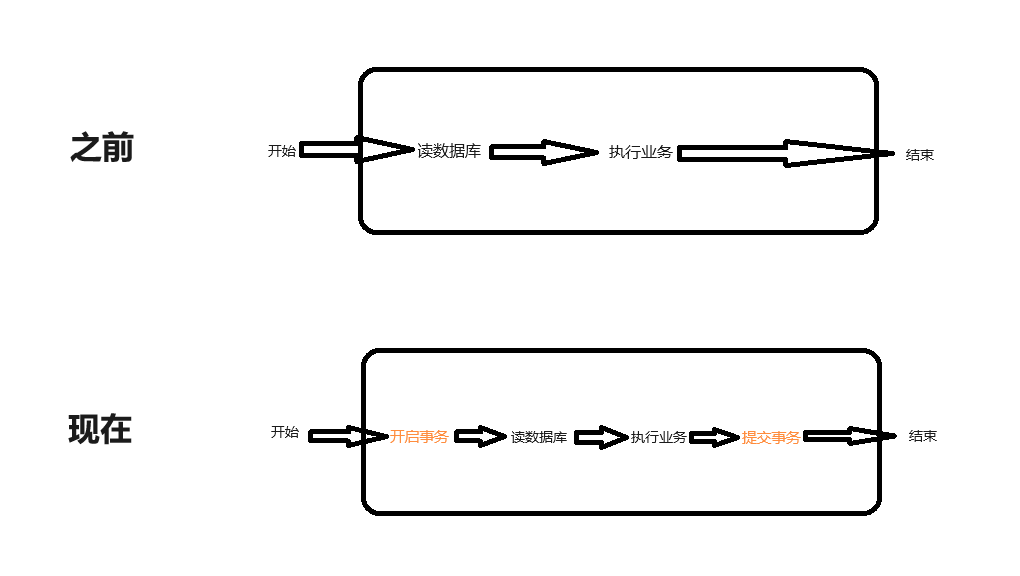
记录一个@Transaction注解引发的bug

记录一个Transactional(readOnly true)注解引发的bug 一、问题代码和报错 1-1 问题代码模拟 引发这个问题的三大要素分别是&#xff1a; 事务注解任意数据库操作数据库操作后执行耗时业务&#xff08;耗时超过数据库配置的超时时间&#xff09; //1.这里是问题的核心之一…...

编程日记 2023/10/15 12:08:10

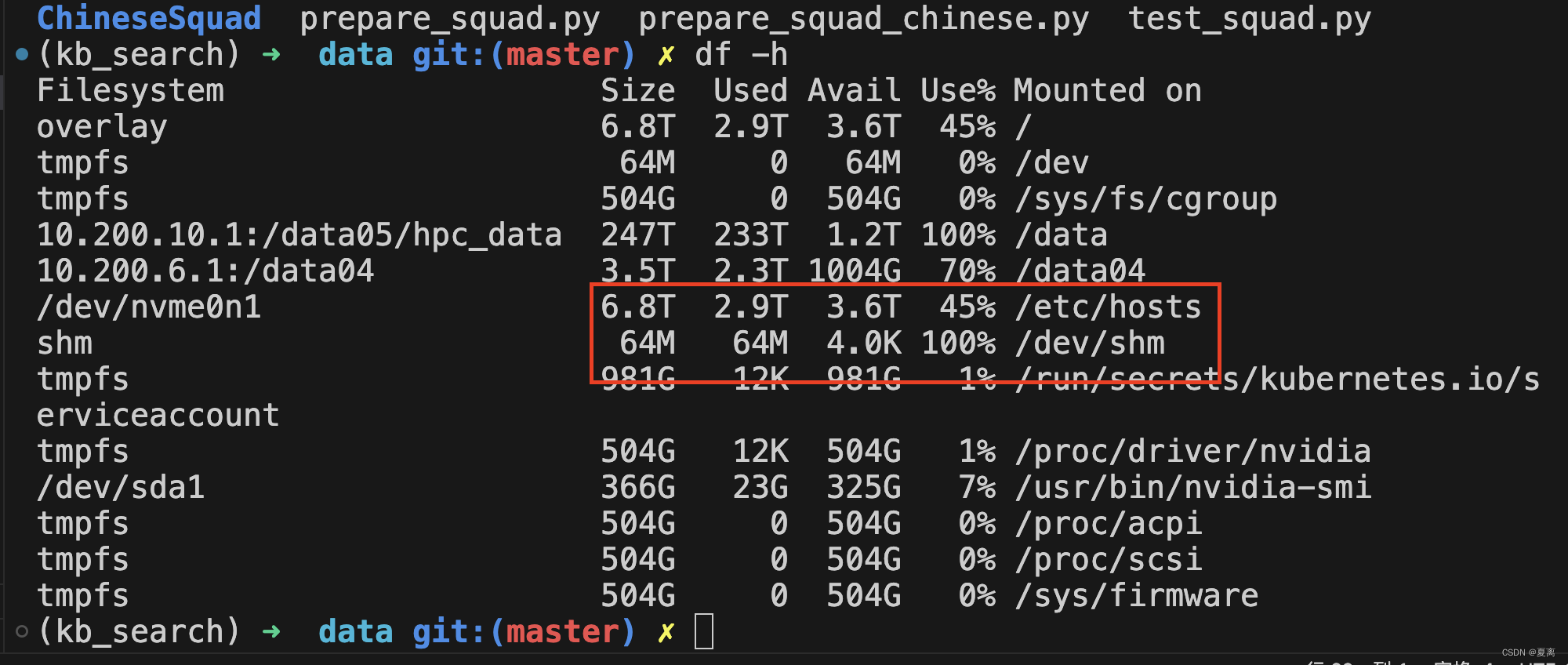
解决docker使用pandarallel报错OSError: [Errno 28] No space left on device

参考&#xff1a;https://github.com/nalepae/pandarallel/issues/127 在使用pandarallel报错OSError: [Errno 28] No space left on device&#xff0c;根据上述issue发现确实默认使用的MEMORY_FS_ROOT为 /dev/shm&#xff0c;而在docker环境下这个目录大小只有64M&#xff0…...

编程日记 2023/10/15 12:07:09

Javascript自定义页面复制事件

Javascript自定义页面复制事件 – WhiteNights Site 2023年10月13日 文章访问量&#xff1a;90 标签&#xff1a;Javascript 监听copy事件以达到自定义页面复制功能的效果。 写者注 需要注意的是&#xff0c;浏览器的部分拓展插件&#xff08;如迅雷&#xff09;会导致本文…...

编程日记 2023/10/15 12:05:07

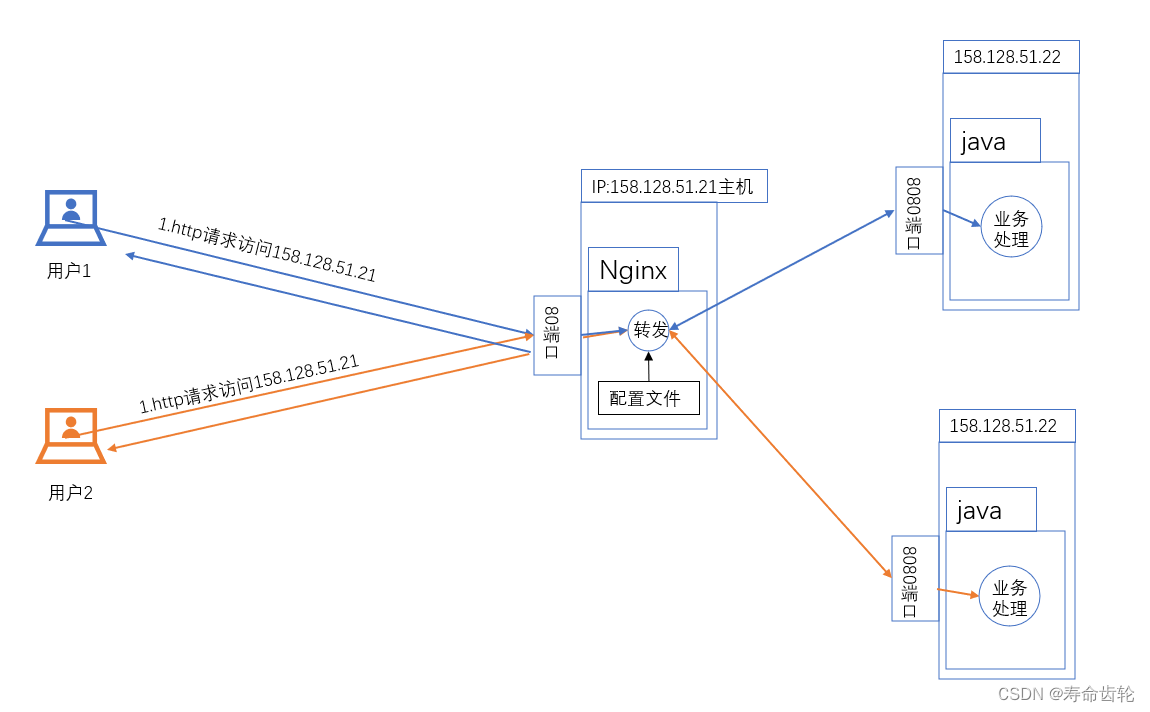
Nginx：反向代理（示意图+配置）

示意图&#xff1a; 反向代理 反向代理&#xff08;Reverse Proxy&#xff09;是代理服务器的一种&#xff0c;它代表服务器接收客户端的请求&#xff0c;并将这些请求转发到适当的服务器。当请求在后端服务器完成之后&#xff0c;反向代理搜集请求的响应并将其传输给客户端。…...

编程日记 2023/10/15 12:04:06

macbook笔记本电脑内存怎么清理才能干净流畅？

假如你还在为“你的系统内存不足”的提示所困扰&#xff0c;或者你的Mac电脑突然运行缓慢和卡顿&#xff0c;那么你一般需要认真了解一下macbook内存怎么清理了? MacBook是功能强大的电脑&#xff0c;这点毫无疑问&#xff0c;但是它仍旧会随着时间推移变得运行缓慢。值得庆幸…...

编程日记 2023/10/15 12:02:04

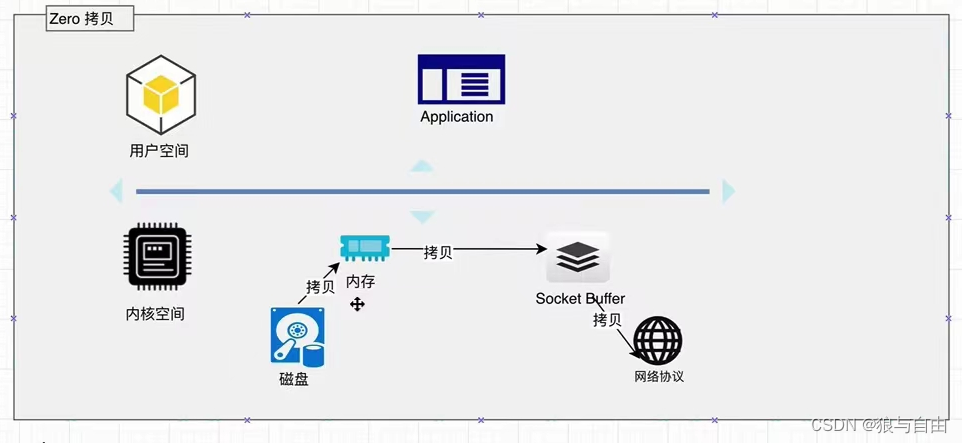
spark 与 mapreduce 对比

Spark 为什么比 MapReduce 快总结 首先澄清几个误区&#xff1a; 1&#xff09;两者都是基于内存计算的&#xff0c;任何计算框架都肯定是基于内存的&#xff0c;所以说网上所说的 Spark 是基于内存计算所以快&#xff0c;显然是错误的。 2&#xff09;DAG 计算模型减少的是磁…...

编程日记 2023/10/15 12:01:03

kafka 相关概念

1 kafka 生产者 kafka 用push的方式把消息推送到topic 每个topic下可以有多个分区&#xff0c; 可以用hash 也可以用轮询的方式指定分区 每个分区内部是可以保证顺序的&#xff0c;但是整体无法保证顺序&#xff0c;除非设置成一个topic只有一个分区。 kafka这种多分区的设置 带…...

编程日记 2023/10/15 12:00:02

Ubuntu下vscode配置OpenCV以及Libtorch

opencv安装 sudo apt-get updatesudo apt-get install libopencv-dev 该方式安装的版本可能比较旧。 测试代码 #include <opencv2/opencv.hpp>#include <iostream>int main() {cv::Mat image cv::imread("t.png");cv::imshow("Image", ima…...

编程日记 2023/10/15 11:59:00

关于共识算法Raft的常见误解

关于共识算法Raft的常见误解 Raft 共识算法最终一致性与线性一致性日志的覆盖与删除Remove节点时需要skip 总结参考文档 Raft 共识算法 最近翻了翻Raft相关的资料&#xff0c;同时也总结了日常工作的一些积累&#xff0c;就当做Raft技术笔记吧。 由于工作的关系&#xff0c;Ra…...

编程日记 2023/10/15 11:57:59

Python学习基础笔记七十——模块和库1

模块和库&#xff1a; 一个python代码文件就实现了功能。功能比较单一。 在企业中&#xff0c;项目开发的文件&#xff0c;可能有成百上千个。 不同的代码文件&#xff0c;实现了不同的功能模块&#xff0c;就像一块块积木一样。这些功能文件整合起来&#xff0c;实现一个完…...

编程日记 2023/10/15 11:56:58

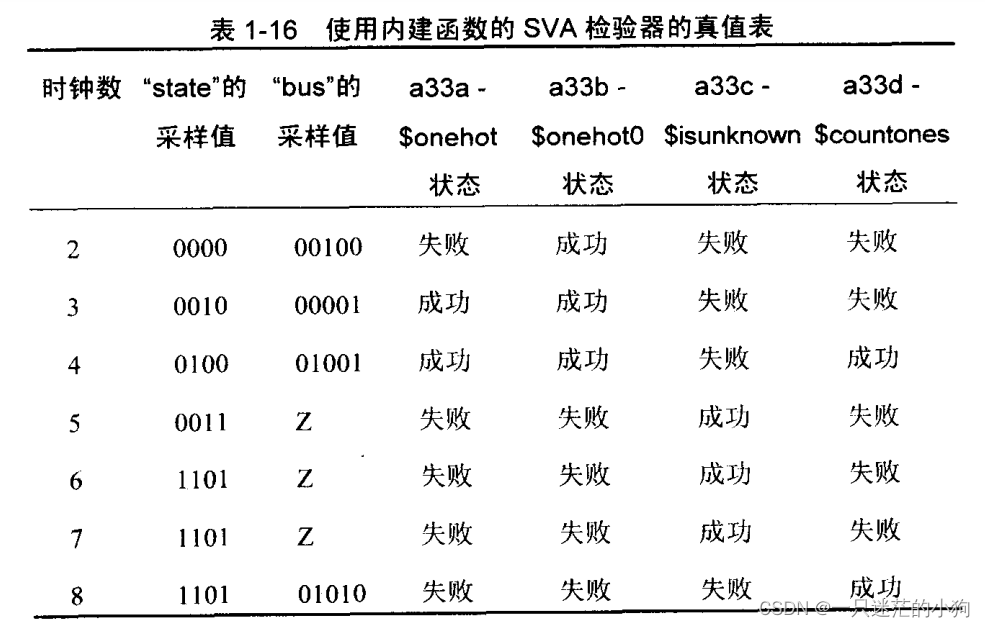
SystemVerilog Assertions应用指南 第一章（1.28章节 内建的系统函数）

SVA提供了几个内建的函数来检查一些最常用的设计条件。 $onehot(expression)—检验表达式满足“one-hot”,换句话说,就是在任意给定的时钟沿,表达式只有一位为高。 $onehot0( expression)—检验表达式满足“ zero one-hot”&#xff0c;换句话说,就是在任意给定…...

编程日记 2023/10/15 11:55:57

3.3.1_1 检错编码（奇偶校验码）

从这节课开始&#xff0c;我们会探讨数据链路层的差错控制功能&#xff0c;差错控制功能的主要目标是要发现并且解决一个帧内部的位错误&#xff0c;我们需要使用特殊的编码技术去发现帧内部的位错误&#xff0c;当我们发现位错误之后&#xff0c;通常来说有两种解决方案。第一…...

编程新知 2026/1/30 3:28:14

【位运算】消失的两个数字（hard）

消失的两个数字&#xff08;hard&#xff09; 题⽬描述&#xff1a;解法&#xff08;位运算&#xff09;&#xff1a;Java 算法代码&#xff1a;更简便代码 题⽬链接&#xff1a;⾯试题 17.19. 消失的两个数字 题⽬描述&#xff1a; 给定⼀个数组&#xff0c;包含从 1 到 N 所有…...

编程新知 2025/11/15 16:18:24

无法与IP建立连接，未能下载VSCode服务器

如题&#xff0c;在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈&#xff0c;发现是VSCode版本自动更新惹的祸&#xff01;&#xff01;&#xff01; 在VSCode的帮助->关于这里发现前几天VSCode自动更新了&#xff0c;我的版本号变成了1.100.3 才导致了远程连接出…...

编程新知 2026/1/22 21:24:01

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案&#xff0c;允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

七、数据库的完整性

七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

编程新知 2026/2/4 10:28:25

AI+无人机如何守护濒危物种？YOLOv8实现95%精准识别

【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而&#xff0c;传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案&#xff0c;能够实现大范围覆盖并远程采集数据。尽管具备这些优势&#xf…...

编程新知 2026/1/26 12:50:00

Vue 3 + WebSocket 实战：公司通知实时推送功能详解

&#x1f4e2; Vue 3 WebSocket 实战&#xff1a;公司通知实时推送功能详解 &#x1f4cc; 收藏 点赞 关注&#xff0c;项目中要用到推送功能时就不怕找不到了&#xff01; 实时通知是企业系统中常见的功能&#xff0c;比如&#xff1a;管理员发布通知后&#xff0c;所有用户…...

编程新知 2025/12/1 3:22:57

起重机起升机构的安全装置有哪些？

起重机起升机构的安全装置是保障吊装作业安全的关键部件&#xff0c;主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理&#xff1a; 一、超载保护装置&#xff08;核心安全装置&#xff09; 1. 起重量限制器 功能&#xff1a;实时监测起升载荷&a…...

编程新知 2025/11/12 16:14:48

算法刷题-回溯

今天给大家分享的还是一道关于dfs回溯的问题&#xff0c;对于这类问题大家还是要多刷和总结&#xff0c;总体难度还是偏大。 对于回溯问题有几个关键点&#xff1a; 1.首先对于这类回溯可以节点可以随机选择的问题&#xff0c;要做mian函数中循环调用dfs&#xff08;i&#x…...

编程新知 2025/10/14 10:53:46

「Java基本语法」变量的使用

变量定义 变量是程序中存储数据的容器&#xff0c;用于保存可变的数据值。在Java中&#xff0c;变量必须先声明后使用&#xff0c;声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例&#xff1a;声明与初始化 public class VariableDemo {publi…...

编程新知 2025/11/19 17:35:31