生信教程:使用拓扑加权探索基因组进化(3)
使用 Twisst 探索整个基因组的进化关系的拓扑加权教程[1]。
简介
拓扑加权是量化不一定是单系群之间关系的一种方法。它通过考虑更简单的“分类单元拓扑”并量化与每个分类单元拓扑匹配的子树的比例,提供了复杂谱系的摘要。我们用来计算权重的方法称为 Twisst:通过子树迭代采样进行拓扑权重。
在本次实践中,我们将使用模拟数据来探索拓扑权重如何提供谱系历史。然后,我们将尝试使用针对窄窗口推断的邻居连接树来推断整个模拟染色体的拓扑权重。
工作流程
我们将通过使用 msprime 运行合并模拟,然后直接从输出计算拓扑权重,来探索人口统计参数如何影响权重,所有这些都在 Python 中进行。
使用树序列格式的拓扑加权
到目前为止,我们已经分析了树文件,这些文件对于具有独特谱系的每个染色体“块”具有独特的树,或者在推断树的情况下对于每个窗口具有独特的树。这种格式有点浪费,因为相邻的树通常非常相似,通常仅因单个重组事件而不同,该重组事件将一个分支从树中的一个点移动到另一个点。
树序列格式非常高效,因为它不仅记录树上节点之间的连接,还记录每个连接所在的染色体的长度。 msprime 和 tskit 包使用此格式,它还提供了更多信息。
模拟树序列
我们将使用 msprime 来模拟树序列。 msprime 是一个合并模拟器,这意味着它的工作原理是计算任意两个个体在过去某个特定时间拥有共同祖先的概率。在单一种群中,这是由种群规模决定的。对于多个种群,这还受到种群之间的迁移率以及它们从单一祖先种群传承多久的影响。
我们将使用 Python 交互式环境来处理 msprime 和树序列,并使用 twisst 中的函数来分析它。
为了确保我们可以从 python 中导入 twisst 模块,请将其添加到我们的 python 路径中。
export PYTHONPATH=$PYTHONPATH:twisst-0.2
现在打开一个Python交互式会话(输入“python”),并在文本编辑器中打开一个脚本,因为我们将多次修改并重新运行其中一些行以测试不同模拟参数的效果 导入所需的模块。
import msprime
import matplotlib.pyplot as plt
import twisst
我们将从对单个总体的 10 个样本进行简单模拟开始。我们必须指定长度和重组率,因此 msprime 将为我们提供一个由多个谱系组成的序列,通过重组分开。在这里,我们还指定了随机种子,只是为了确保在这种情况下我们都得到相同的模拟。
ts = msprime.simulate(sample_size=10,
Ne=1000,
length=10000,
recombination_rate=5e-8,
random_seed = 1)
我们可以检查树序列中有多少个不同的家谱。
ts.num_trees
并使用树序列对象提供的良好可视化方法来查看它们。
for tree in ts.trees():
print("interval = ", tree.interval)
print(tree.draw(format="unicode"))
包含四个种群和基因流的模拟
我们现在将建立一个包含多个群体的更大的模拟。这需要一些不同的组件,我们将分别定义它们。首先,我们定义样本数量和每个总体的总体规模。
pop_n = 10
pop_Ne = 10000
population_configurations = [msprime.PopulationConfiguration(sample_size=pop_n, initial_size=pop_Ne),
msprime.PopulationConfiguration(sample_size=pop_n, initial_size=pop_Ne),
msprime.PopulationConfiguration(sample_size=pop_n, initial_size=pop_Ne),
msprime.PopulationConfiguration(sample_size=pop_n, initial_size=pop_Ne)]
接下来我们设置种群之间的迁移率。这些可以以 4x4 矩阵的形式定义,每个条目给出从另一个群体(行)迁移到另一个群体(列)的速率。这里我们设定第二和第三种群之间双向适度迁移,其他种群之间不迁移。该值代表m,即每代移民占人口的比例。
migration_matrix = [[0, 0, 0, 0],
[0, 0, 1e-4, 0],
[0, 1e-4, 0, 0],
[0, 0, 0, 0]]
最后,我们设置了分割时间,在合并世界观中,这些时间是时间倒流的连接。在 msprime 中,这些称为大规模迁移。因此,前两个种群之间的分裂被建模为所有个体从第二个种群到第一个种群的大规模迁移(称为 0 和 1,因为 Python 从 0 开始编号)。再往前追溯,种群 2 和 3 也大规模迁移到种群 0。在第一个事件(时间向后)之后,我们还关闭了 1 和 2 之间的迁移。
t_01 = 1000
t_02 = 5000
t_03 = 10000
demographic_events = [msprime.MassMigration(time=t_01, source=1, destination=0, proportion=1.0), # first merge
msprime.MigrationRateChange(time=t_01, rate=0, matrix_index=(2, 1)), # mig stop after merge
msprime.MigrationRateChange(time=t_01, rate=0, matrix_index=(1, 2)),
msprime.MassMigration(time=t_02, source=2, destination=0, proportion=1.0), #next merge
msprime.MassMigration(time=t_03, source=3, destination=0, proportion=1.0)] #final merge
现在我们准备模拟树序列。我们将长度设置为 50 kb,重组率为 5e-8。 msprime 速度非常快!
ts = msprime.simulate(population_configurations = population_configurations,
migration_matrix = migration_matrix,
demographic_events = demographic_events,
length = 50000,
recombination_rate = 5e-8
)
我们可以再次检查树的数量
ts.num_trees
而且,如果我们敢的话,我们可以看看树序列中的第一棵树:
print(ts.first().draw(format="unicode"))
从树序列计算权重
然后运行 twist 中的函数来计算树序列的权重。我们不需要指定组,因为该信息已由 msprime 包含在树序列对象中。但我们仍然需要告诉它使用最终的总体(数字 3,因为 python 从 0 开始计数)。
weightsData = twisst.weightTrees(ts, treeFormat="ts", outgroup = "3", verbose=False)
我们可以快速总结平均权重
twisst.summary(weightsData)
我们还可以直接快速保存权重图(这节省了导出到文件并在 R 中绘制精美图的时间)
#extract mid positions on chromosome from tree sequence file
position = [(tree.interval[0] + tree.interval[1])/2 for tree in ts.trees()]
#normalise weights by dividing by number of combinations
weights = weightsData["weights"]/10000
#create a plot with all three topology weights
for i in range(3):
plt.plot(position, weights[:,i], label='topo'+str(i+1))
plt.legend()
#save plot
plt.savefig('sim_ts_weights.pdf')
完!
Reference
Source: https://github.com/simonhmartin/tutorials/blob/master/topology_weighting/README.md
本文由 mdnice 多平台发布
相关文章:
)
生信教程:使用拓扑加权探索基因组进化(3)
使用 Twisst 探索整个基因组的进化关系的拓扑加权教程[1]。 简介 拓扑加权是量化不一定是单系群之间关系的一种方法。它通过考虑更简单的“分类单元拓扑”并量化与每个分类单元拓扑匹配的子树的比例,提供了复杂谱系的摘要。我们用来计算权重的方法称为 Twisst&#…...

React js原生 详解 HTML 拖放 API(鼠标拖放功能)
最近碰到了个需求,大概就是要通过可视化拖拽的方式配置一个冰柜,需要把预设好的冰柜内部架子模板一个个拖到冰箱内。一开始的想法是用鼠标事件(mousedown、mouseup等)那一套去实现,能实现但是过程过于复杂,…...
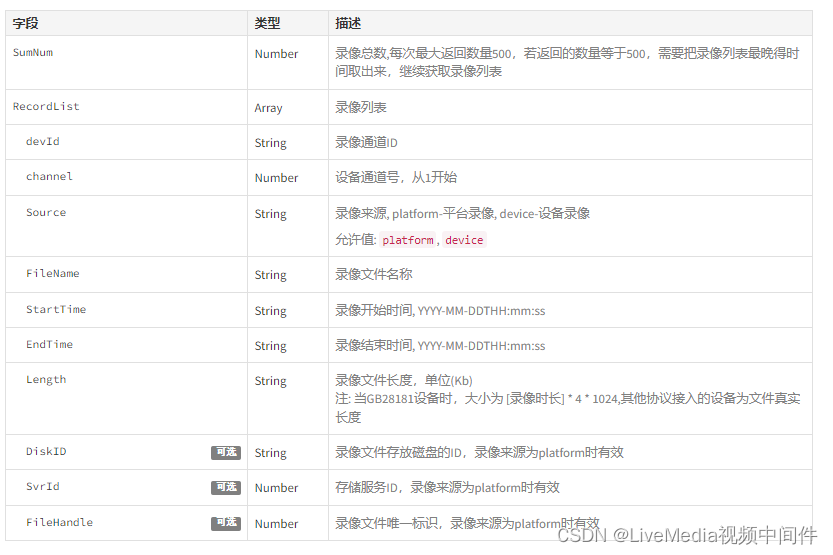
LiveMedia视频中间件如何与第三方系统实现事件录像关联
一、平台简介 LiveMedia视频中间件是支持部署到本地服务器或者云服务器的纯软件服务,也提供服务器、GPU一体机全包服务,提供视频设备管理、无插件、跨平台的实时视频、历史回放、语音对讲、设备控制等基础功能,支持视频协议有海康、大华私有协…...

机器学习-有监督算法-决策树和支持向量机
目录 决策树ID3C4.5CART 支持向量积 决策树 训练:构造树,测试:从模型从上往下走一遍。建树方法:ID3,C4.5,CART ID3 以信息论为基础,以信息增益为衡量标准熵越小,混乱程度越小&…...

luffy项目之后台项目搭建、目录调整、封装日志、全局异常、Response、数据库连接
luffy后台项目创建 在虚拟环境中创建luffy项目安装django:pip install django3.1.12命令创建项目django-admin startproject luffy_api也可以pycharm创建项目,创建项目时选则已经创建好的虚拟环境即可 luffy项目目录调整 """ ├── …...
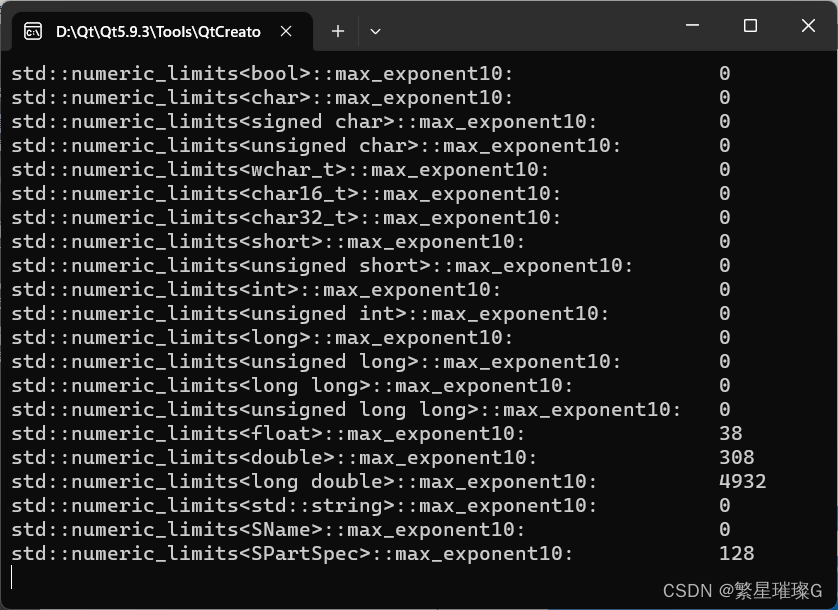
C++标准模板(STL)- 类型支持 (数值极限,min_exponent10,max_exponent,max_exponent10)
数值极限 std::numeric_limits 定义于头文件 <limits> 定义于头文件 <limits> template< class T > class numeric_limits; numeric_limits 类模板提供查询各种算术类型属性的标准化方式(例如 int 类型的最大可能值是 std::numeric_limits&l…...
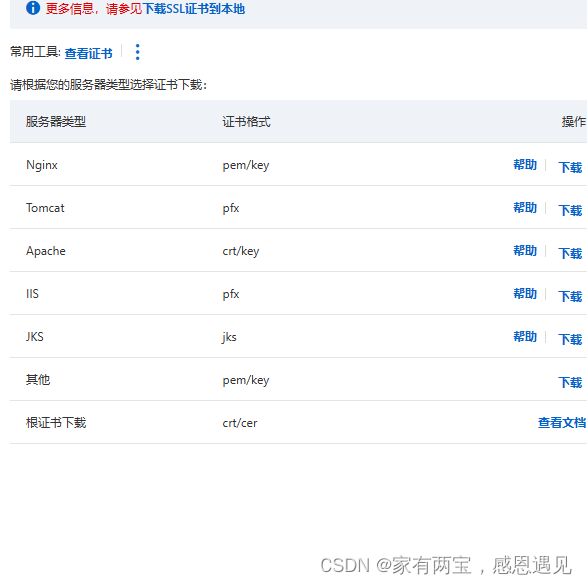
linux 服务器类型Apache配置https访问
一:查看服务器类型,下载相应的SSL证书 命令:netstat -anp | grep :80 httpd是Apache超文本传输协议(HTTP)服务器的主程序,所以下载Apache证书 二:将证书解压后复制到服务器上 三个文件:xxx.key xxx_publ…...
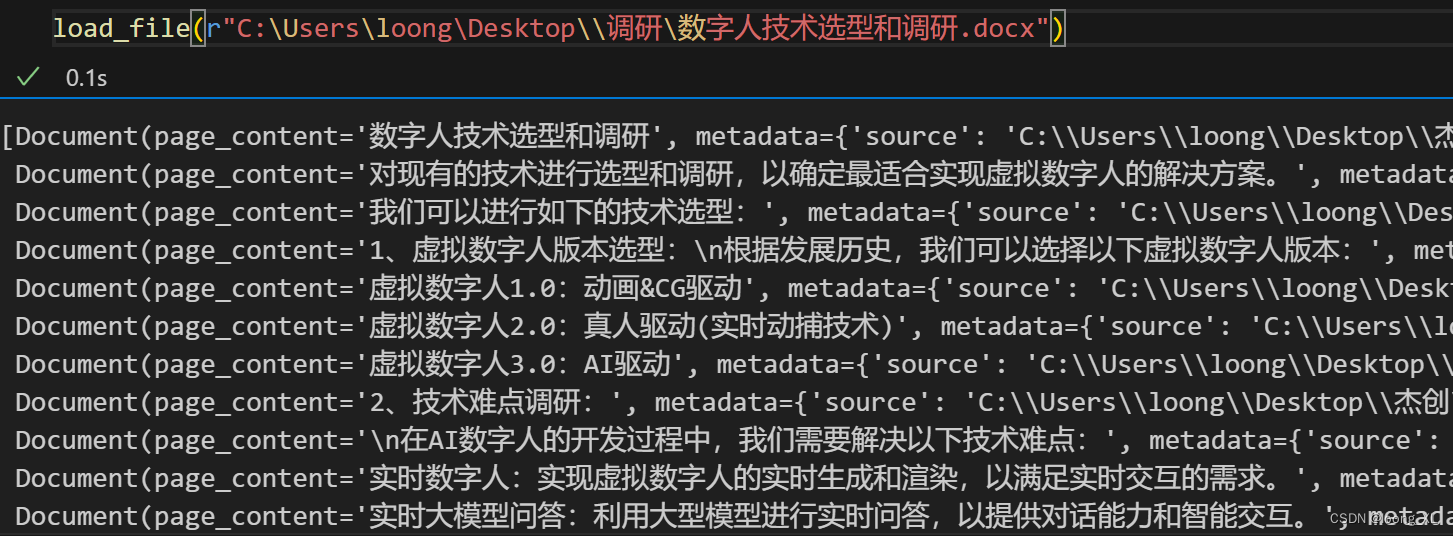
langchain 加载各种格式文件读取方法
参考:https://python.langchain.com/docs/modules/data_connection/document_loaders/ https://github.com/thomas-yanxin/LangChain-ChatGLM-Webui/blob/master/app.py 代码 可以支持pdf、md、doc、txt等格式 from langchain.document_loaders import Unstruct…...
飞花令游戏(Python)
飞花令是古时候人们经常玩一种“行酒令”的游戏,是中国古代酒令之一,属雅令。“飞花”一词则出自唐代诗人韩翃《寒食》中 春城无处不飞花 一句。行飞花令时选用诗和词,也可用曲,但选择的句子一般不超过7个字。 在《中国诗词大会》…...
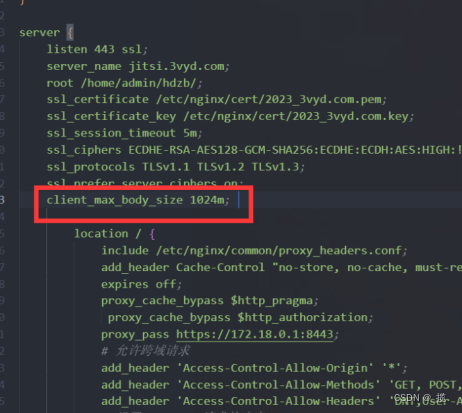
解决“413 Request Entity Too Large”错误 代表请求包太大,服务器拒绝响应
解决办法: 在nginx的配置文件nginx.conf中,添加这么一句client_max_body_size 1024m; 意思是最大请求是1024m。这个配置可以放到 http段 或者 server段 或者 location段。...
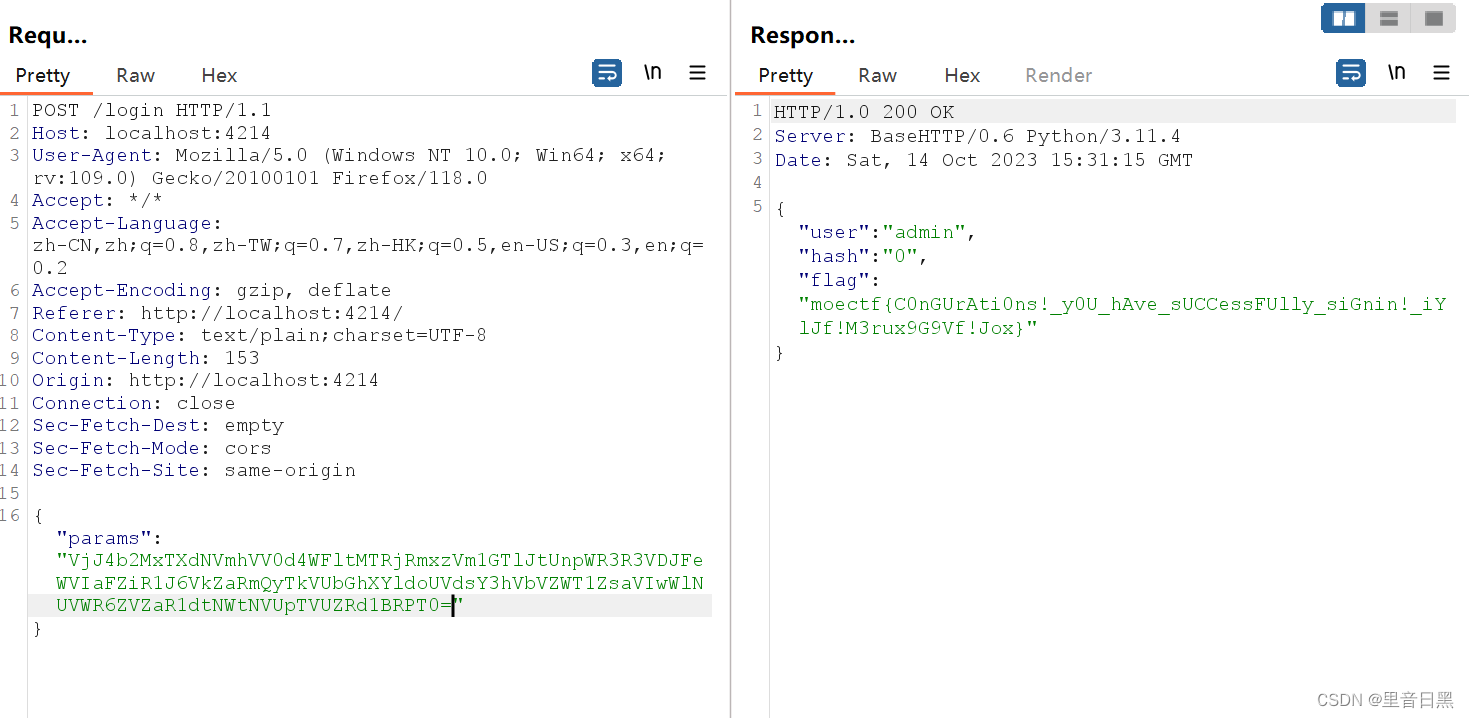
MoeCTF2023web
01http 打开题目环境 可以看到要求完成所有任务,这里用burp抓个包 按照要求修改可以得到flag moectf{basic_http_knowledge_HJbg427uFuznTqiJdtS1xhZNwpdsOnKU} 02 Web入门指北 直接找到结尾发现乱码,去解码 编码可以试试url编码和base64到16 这里用…...
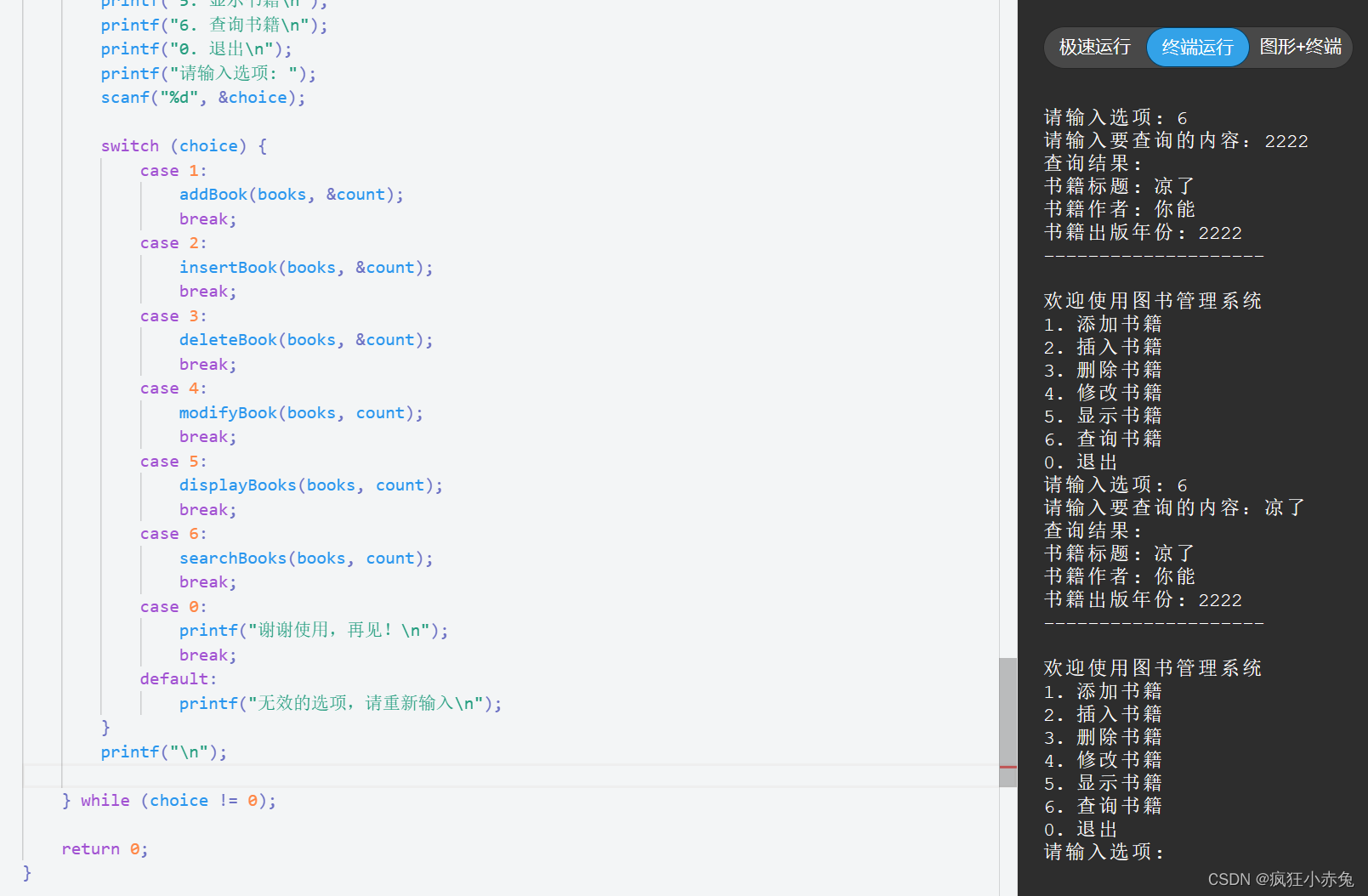
C语言编写简易图书管理系统
这篇文章介绍了一个基本的图书管理系统的实现,它允许用户添加、插入、删除、修改、显示和查询图书的功能。该系统通过使用二进制文件将图书信息保存到磁盘,并且在程序启动时能够加载已保存的图书信息。 介绍 在计算机科学中,图书管理系统是…...
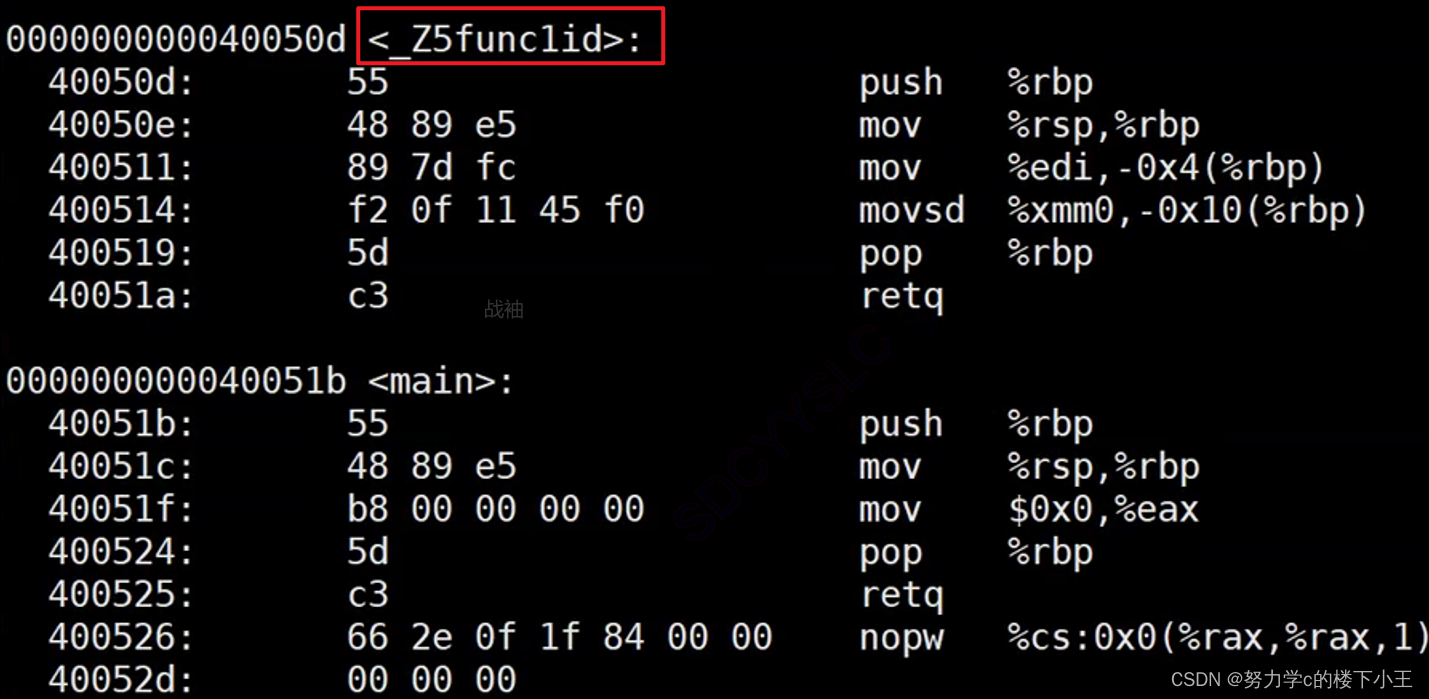
C++入门 第一篇(C++关键字, 命名空间,C++输入输出)
目录 1. C关键字 2. 命名空间 2.1 命名空间定义 2.2命名空间的使用 命名空间的使用有三种方式: 1.加命名空间名称及作用域限定符 2.使用using将命名空间中某个成员引入 3.使用using namespace 命名空间名称 引入 3. C输入&输出 4.缺省函数 4.1 缺省参…...

python股票波动性分析
一、简介 我们都经历过这样的情况——盯着股票图表,试图理解那些疯狂的价格上涨,或者只是想知道为什么突然平静。在这些波动中,有一个一致的因素常常脱颖而出:波动性。了解波动性为衡量任何特定点的市场情绪和情绪提供了一个视角。通过剖析波动性的细微差别,我们不仅可以更…...

53 打家劫舍
打家劫舍 题解1 DP1题解2 DP2 !经典DP! 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果 两间相邻的房屋在同一晚上被小偷闯入…...
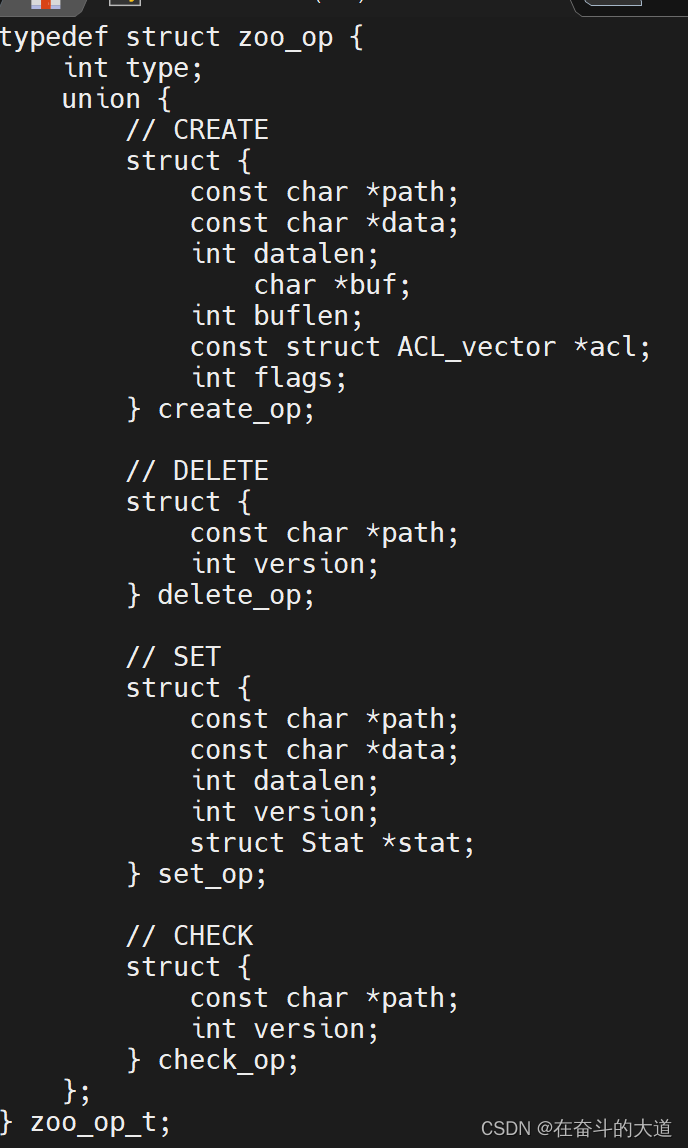
CentOS 7 基于C 连接ZooKeeper 客户端
前提条件:CentOS 7 编译ZooKeeper 客户端,请参考:CentOS 7 编译ZooKeeper 客户端 1、Docker 安装ZooKeeper # docker 获取zookeeper 最新版本 docker pull zookeeper# docker 容器包含镜像查看 docker iamges# 准备zookeeper 镜像文件挂载对…...

2023-2024-1 for循环-1(15-38)
7-15 输出闰年 输出21世纪中截止某个年份以来的所有闰年年份。注意:闰年的判别条件是该年年份能被4整除但不能被100整除、或者能被400整除。 输入格式: 输入在一行中给出21世纪的某个截止年份。 输出格式: 逐行输出满足条件的所有闰年年份,即每个年…...
初级问题 程序中的变量是指什么?中级问题 把若干个数据沿直线排列起来的数据结构叫作什么?高级问题 栈和队列的区别是什么?
目录 1.深刻主题 2.描写复杂人物 初级问题 程序中的变量是指什么? 中级问题 把若干个数据沿直线排列起来的数据结构叫作什么? 高级问题 栈和队列的区别是什么? 计算机图形学(有效边表算法) 介绍一下计算机图形学…...

clickhouse数据库简介,列式存储
clickhouse数据库简介 1、关于列存储 所说的行式存储和列式存储,指的是底层的存储形式,数据在磁盘上的真实存储,至于暴漏在上层的用户的使用是没有区别的,看到的都是一行一行的表格。 idnameuser_id1闪光10266032轨道物流10265…...

flask 发送ajax
前端 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body> <script src"https://cdn.lyshark.com/javascript/jquery/3.5.1/jquery.min.js"…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
