【Codeforces】 CF1097G Vladislav and a Great Legend
题目链接
CF方向
Luogu方向
题目解法
首先一个套路是普通幂转下降幂(为什么?因为观察到 k k k 很小,下降幂可以转化组合数问题,从而 d p dp dp 求解)
即 f ( X ) k = ∑ i = 0 k { k i } i ! ( f ( X ) i ) f(X)^k=\sum\limits_{i=0}^{k}{k\brace i}i!\binom{f(X)}{i} f(X)k=i=0∑k{ik}i!(if(X))
现在的问题是对于所有生成树求出中间选 i i i 条边的方案数
我们令非空顶点的点集为关键点,其他生成树上的点为包含点
考虑树形 d p dp dp,令 f i , j f_{i,j} fi,j 表示在 i i i 的子树中选出至少 1 1 1 个关键点,且与 i i i 连通的生成树中选出 j j j 条边的方案数
考虑转移:
- v v v 子树中没有关键点
f u , i → f u , i f_{u,i}\to f_{u,i} fu,i→fu,i,不能计入答案计算,因为没有改变关键点集合 - 只有 v v v 子树中的关键点组成
f v , i + f v , i − 1 → f u , i f_{v,i}+f_{v,i-1}\to f_{u,i} fv,i+fv,i−1→fu,i,不能计入答案计算,因为这个关键点集合在 v v v 时已经计算过 - u , v u,v u,v 子树中均有关键点
f u , i ∗ f v , j → f u , i + j & f u , i + j + 1 f_{u,i}*f_{v,j}\to f_{u,i+j}\&f_{u,i+j+1} fu,i∗fv,j→fu,i+j&fu,i+j+1,可以计入答案计算,因为改变了关键点集合
根据树形 d p dp dp 的时间复杂度计算,时间复杂度为 O ( n k ) O(nk) O(nk)
#include <bits/stdc++.h>
using namespace std;
const int N=100100,K=210,P=1e9+7;
int n,k,siz[N],s2[K][K],t[N],ans[N];
int ne[N<<1],e[N<<1],h[N],idx;
int f[N][K];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
inline void inc(int &x,int y){ x+=y;if(x>=P) x-=P;}
void dfs(int u,int fa){siz[u]=1,f[u][0]=1;for(int i=h[u];~i;i=ne[i]){int v=e[i];if(v==fa) continue;dfs(v,u);for(int j=0;j<=k;j++) t[j]=f[u][j];for(int j=0;j<=k;j++){inc(t[j],f[v][j]);if(j) inc(t[j],f[v][j-1]);}for(int p=0,mxp=min(k,siz[u]);p<=mxp;p++) for(int q=0,mxq=min(k-p,siz[v]);q<=mxq;q++){int coef=1ll*f[u][p]*f[v][q]%P;inc(t[p+q],coef),inc(t[p+q+1],coef);inc(ans[p+q],coef),inc(ans[p+q+1],coef);}siz[u]+=siz[v];for(int j=0;j<=k;j++) f[u][j]=t[j];}
}
int main(){n=read(),k=read();s2[0][0]=1;for(int i=1;i<=k;i++) for(int j=1;j<=i;j++) s2[i][j]=(s2[i-1][j-1]+1ll*s2[i-1][j]*j)%P;memset(h,-1,sizeof(h));for(int i=1;i<n;i++){int x=read(),y=read();add(x,y),add(y,x);}dfs(1,-1);int ANS=0;for(int i=1,fac=1;i<=k;i++,fac=1ll*fac*i%P) ANS=(ANS+1ll*ans[i]*s2[k][i]%P*fac)%P;printf("%d\n",ANS);return 0;
}相关文章:

【Codeforces】 CF1097G Vladislav and a Great Legend
题目链接 CF方向 Luogu方向 题目解法 首先一个套路是普通幂转下降幂(为什么?因为观察到 k k k 很小,下降幂可以转化组合数问题,从而 d p dp dp 求解) 即 f ( X ) k ∑ i 0 k { k i } i ! ( f ( X ) i ) f(X)^k…...

力扣每日一题36:有效的数独
题目描述: 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考…...
钉钉数字校园小程序开发:开启智慧教育新时代
随着信息技术的快速发展和校园管理的日益复杂化,数字校园已成为现代教育的重要趋势。钉钉数字校园小程序作为一种创新应用,以其专业性、思考深度和逻辑性,为学校提供了全新的管理、教学和沟方式。本文从需求分析、技术实现和应用思考三个方面…...

数据结构与算法--其他算法
数据结构与算法--其他算法 1 汉诺塔问题 2 字符串的全部子序列 3 字符串的全排列 4 纸牌问题 5 逆序栈问题 6 数字和字符串转换问题 7 背包问题 8 N皇后问题 暴力递归就是尝试 1,把问题转化为规模缩小了的同类问题的子问题 2,有明确的不需要继续…...

矩阵键盘行列扫描
/*----------------------------------------------- 内容:如计算器输入数据形式相同 从右至左 使用行列扫描方法 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含…...
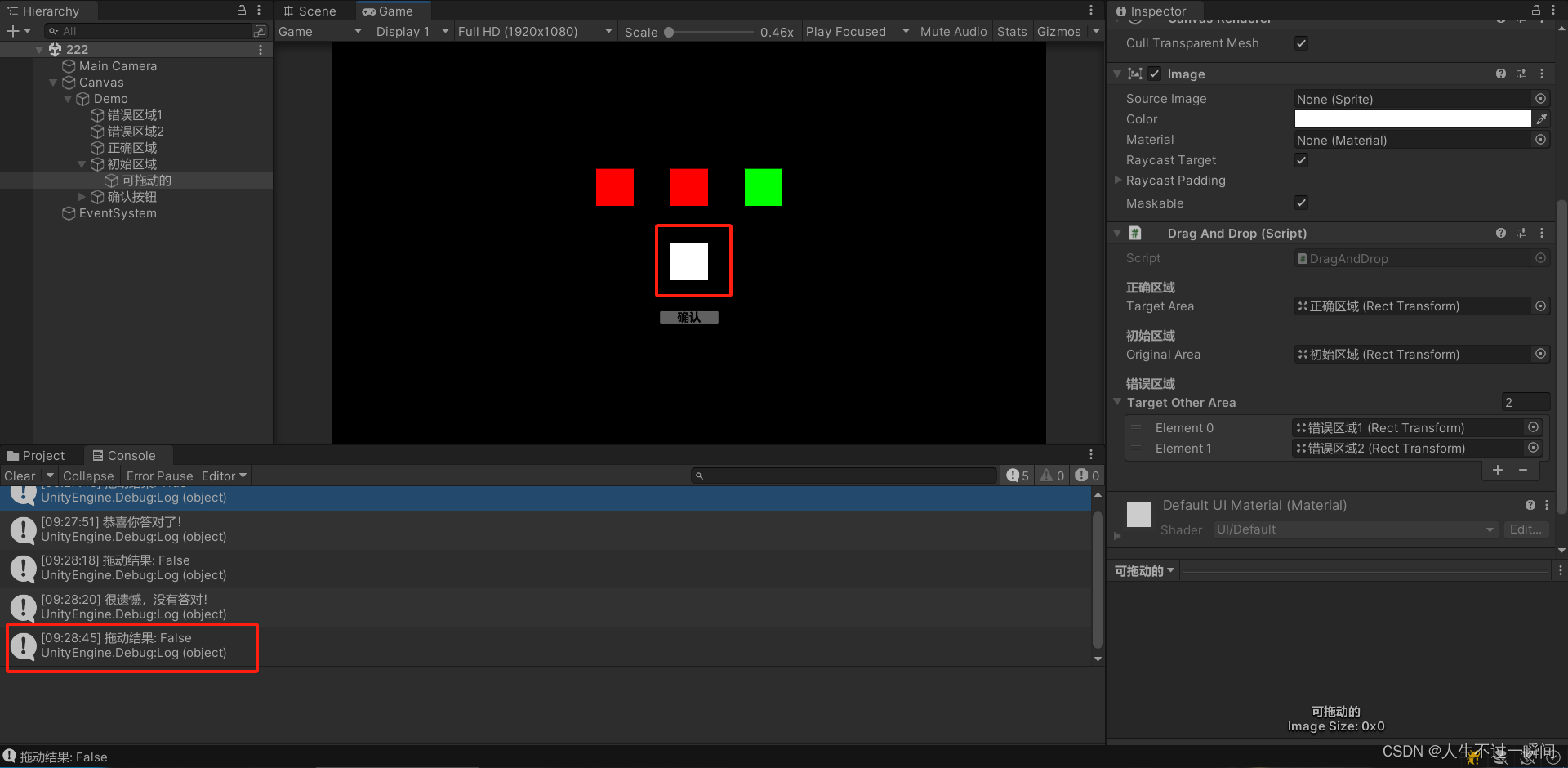
unity 实现拖动ui填空,并判断对错
参考:https://ask.csdn.net/questions/7971448 根据自己的需求修改为如下代码 使用过程中,出现拖动ui位置错误的情况,修改为使用 localPosition 但是吸附到指定位置却需要用的position public class DragAndDrop : MonoBehaviour, IBeginDr…...
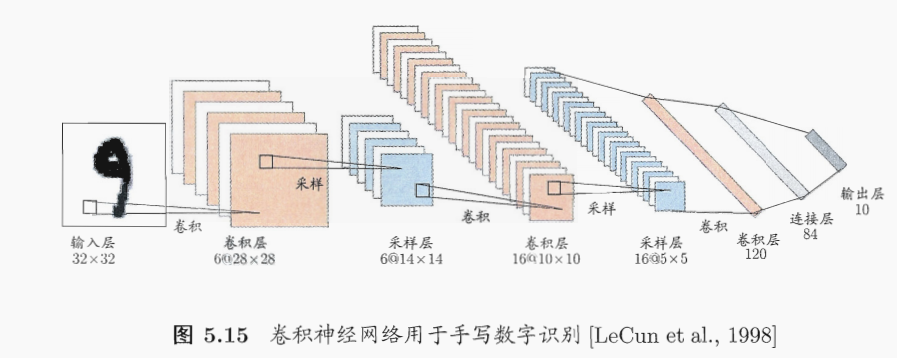
《机器学习》第5章 神经网络
文章目录 5.1 神经元模型5.2 感知机与多层网络5.3 误差逆传播算法5.4 全局最小与局部最小5.5 其他常见神经网络RBF网络ART网络SOM网络级联相关网络Elman网络Boltzmann机 5.6 深度学习 5.1 神经元模型 神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它…...
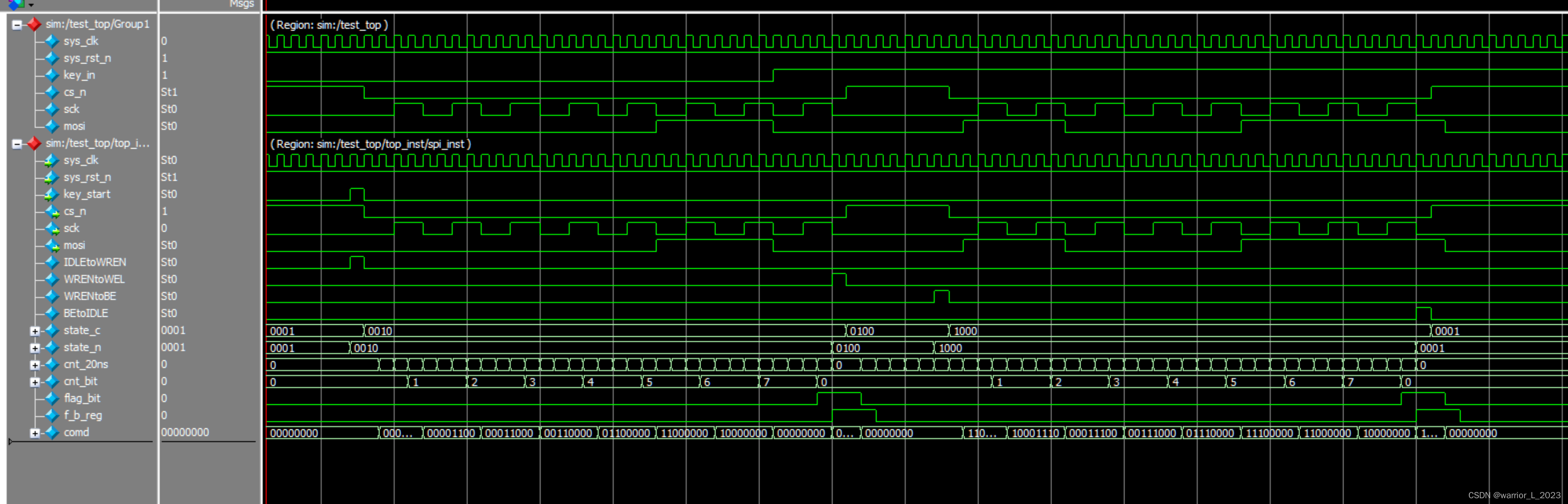
FPGA project : flash_erasure
SPI是什么: SPI(Serial Peripheral Interface,串行外围设备接口)通讯协议,是Motorola公司提出的一种同步串行接口技术,是一种高速、全双工、同步通信总线,在芯片中只占用四根管脚用来控制及数据…...
AC修炼计划(AtCoder Regular Contest 166)
传送门:AtCoder Regular Contest 166 - AtCoder 一直修炼cf,觉得遇到了瓶颈了,所以想在atcode上寻求一些突破,今天本来想尝试vp AtCoder Regular Contest 166,但结局本不是很好,被卡了半天,止步…...
Android---Android 是如何通过 Activity 进行交互的
相信对于 Android 工程师来说,startActivity 就像初恋一般。要求低,见效快,是每一个菜鸟 Android 工程师迈向高级 Android 工程师的必经阶段。经过这么多年的发展,startActivity 在 google 的调教下已经变得愈发成熟,对…...

【论文解读】单目3D目标检测 MonoCon(AAAI2022)
本文分享单目3D目标检测,MonoCon模型的论文解读,了解它的设计思路,论文核心观点,模型结构,以及效果和性能。 目录 一、MonoCon简介 二、论文核心观点 三、模型框架 四、模型预测信息与3D框联系 五、损失函数 六、…...
-每天10个小知识)
Angular知识点系列(5)-每天10个小知识
目录 41. Angular的路由守卫42. 处理文件的上传和下载43. Angular的动画系统44. 使用第三方库和选择评估45. 性能优化46. AOT和JIT编译47. 处理响应式布局和适配不同屏幕尺寸48. Angular的国际化(i18n)49. Angular的PWA开发50. 使用Angular Material或其…...

基于海洋捕食者优化的BP神经网络(分类应用) - 附代码
基于海洋捕食者优化的BP神经网络(分类应用) - 附代码 文章目录 基于海洋捕食者优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.海洋捕食者优化BP神经网络3.1 BP神经网络参数设置3.2 海洋捕食者算法应用 4…...

Lift, Splat, Shoot图像BEV安装与模型详解
1 前言 计算机视觉算法通常使用图像是作为输入并输出预测的结果,但是对结果所在的坐标系却并不关心,例如图像分类、图像分割、图像检测等任务中,输出的结果均在原始的图像坐标系中。因此这种范式不能很好的与自动驾驶契合。 在自动驾驶中,多个相机传感器的数据一起作为输…...

MySQL简介
数据库管理系统 1、关系型数据库管理系统: Oracle:Oracle是一种商业级关系型数据库管理系统,支持高可用性、高安全性以及广泛的企业级应用需求。SQL Server:SQL Server是Microsoft开发的企业级关系型数据库管理系统,广泛应用于Windows环境下的软件开发。MySQL:MySQL是一…...

php代码优化---本人的例子
直接上货: 1:数据统计 店铺数量、提现金额、收益金额、用户数量 旧: // //店铺// $storey db( store )->whereTime( addtime, yesterday )->count();//昨天// $stored db( store )->whereTime( addtime, d )->count();//今天…...

EMC Unity存储(VNXe) service Mode和Normal Mode的一些说明
本文介绍下EMC unity存储设备(也包含VNXe存储设备)的两种工作模式: Service mode:也叫做rescue mode,存储OS工作不正常或者有其他故障,就会进入这个模式,无法对外提供服务Normal modeÿ…...
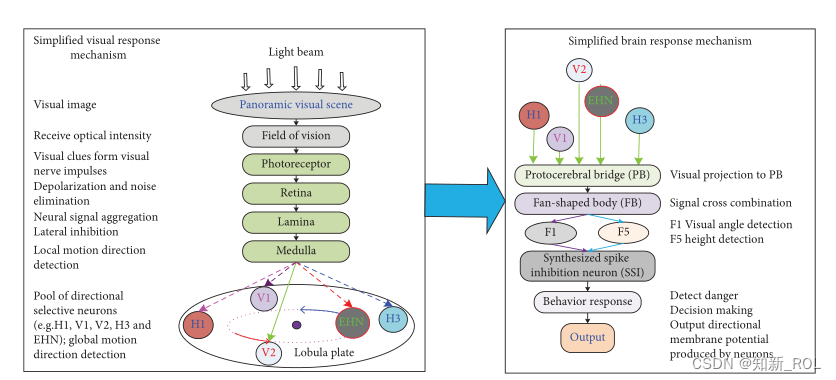
基于全景运动感知的飞行视觉脑关节神经网络全方位碰撞检测
https:/doi.org/10.1155/2023/5784720 摘要: 生物系统有大量的视觉运动检测神经元,其中一些神经元可以优先对特定的视觉区域做出反应。然而,关于如何使用它们来开发用于全向碰撞检测的神经网络模型,很少有人做过工作。为此&#…...
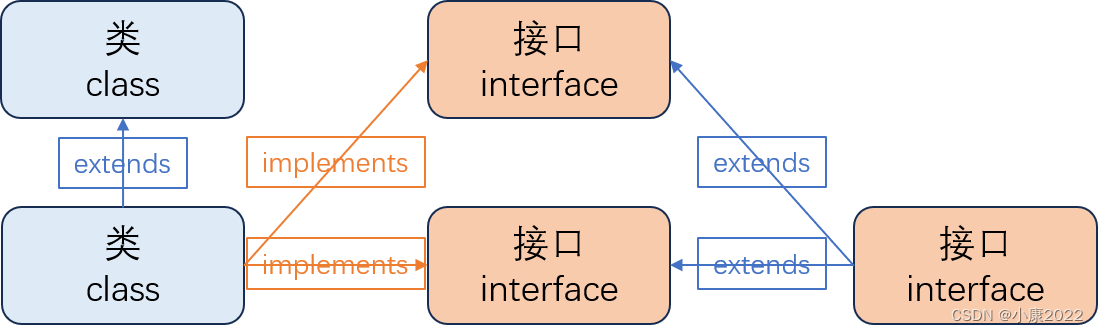
Java 继承与实现
一、继承(extends) 1.1 继承概念 继承是面向对象的基本特征,它允许子类继承父类的特征和行为,以提高代码的复用率和维护性等。下面一张图生动地展示了继承和类之间的关系: 继承图 上图中,“动物”、“食草…...
Unity 3D基础——计算两个物体之间的距离
1.在场景中新建两个 Cube 立方体,在 Scene 视图中将两个 Cude的位置错开。 2.新建 C# 脚本 Distance.cs(写完记得保存) using System.Collections; using System.Collections.Generic; using UnityEngine;public class Distance : MonoBehav…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
