当前位置： 首页 > news >正文

自然语言处理（NLP）-概述

news 2026/2/10 16:58:54

NLP

  • 一、什么是自然语言处理（NLP）
  • 二、NLP的发展
  • 三、相关理论
    • 1 语言模型
    • 2 词向量表征和语义分析
    • 3 深度学习

一、什么是自然语言处理（NLP）

什么是自然语言处理

二、NLP的发展

三、相关理论

1 语言模型

序列数据形式多样，如视频帧、音频数据等，其中文本是最常见的。
文本预处理：

  • 1 将文本作为字符串加载到内存中。
  • 2 将字符串拆分为词元（如单词和字符）。
  • 3 建立一个词表，将拆分的词元映射到数字索引。
  • 4 将文本转换为数字索引序列，方便模型操作。

假设长度为T的文本序列中的词元依次为 x 1 , x 2 , … , x T x_1, x_2, \ldots, x_T x1​,x2​,…,xT​。 于是 x t , 1 ≤ t ≤ T x_t, 1 \leq t \leq T xt​,1≤t≤T， 可以被认为是文本序列在时间步t处的观测或标签。 在给定这样的文本序列时，语言模型（language model） 的目标是估计序列的联合概率 P ( x 1 , x 2 , … , x T ) . P(x_1, x_2, \ldots, x_T). P(x1​,x2​,…,xT​).

2 词向量表征和语义分析

3 深度学习

相关文章：

自然语言处理（NLP）-概述

NLP 一、什么是自然语言处理（NLP）二、NLP的发展三、相关理论1 语言模型2 词向量表征和语义分析3 深度学习 一、什么是自然语言处理（NLP） 什么是自然语言处理 二、NLP的发展 三、相关理论 1 语言模型 序列数据形式多样&#xf…...

编程日记 2023/10/15 14:57:21

Python开发者的宝典：CSV和JSON数据处理技巧大公开！

更多资料获取 📚 个人网站：涛哥聊Python 在Python中处理CSV和JSON数据时，需要深入了解这两种数据格式的读取、写入、处理和转换方法。 下面将详细介绍如何在Python中处理CSV和JSON数据，并提供一些示例和最佳实践。 CSV数据处理…...

编程日记 2023/10/15 14:56:20

Unity中Commpont类获取子物体的示例

// 本脚本用于演示Component类 方法 //任何一个组件 都可以从游戏物体获取或者从其父对象哪里 子对象哪里获取，一个组件也可以拿到同一个物体上的其他组件 using System.Collections; using System.Collections.Generic; using UnityEngine; public class Component…...

编程日记 2023/10/15 14:55:19

【Vue面试题二十一】、Vue中的过滤器了解吗？过滤器的应用场景有哪些？

文章底部有个人公众号：热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享？ 踩过的坑没必要让别人在再踩，自己复盘也能加深记忆。利己利人、所谓双赢。 面试官：Vue中的过滤器了解吗&am…...

编程日记 2023/10/15 14:54:17

Unity 3D基础——缓动效果

1.在场景中新建两个 Cube 立方体，在 Scene 视图中将两个 Cude的位置错开。 2.新建 C# 脚本 MoveToTarget.cs（写完记得保存） using System.Collections; using System.Collections.Generic; using UnityEngine;public class MoveToTarget : M…...

编程日记 2023/10/15 14:53:16

高校教务系统登录页面JS分析——南京邮电大学

高校教务系统密码加密逻辑及JS逆向 本文将介绍南京邮电大学教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文，你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习，勿用于非法用途。 一…...

编程日记 2023/10/15 14:52:15

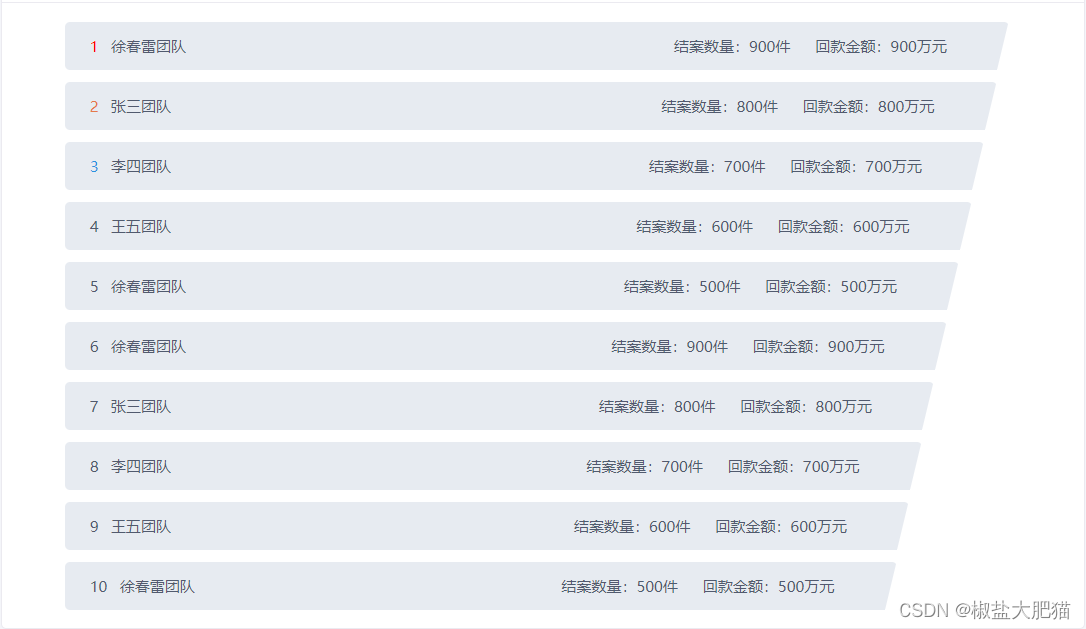
css实现排行榜样式（vue组件）

先看效果图&#xff1a; <template><div class"lawyer-refund-wrap"><div class"content"><divv-for"(item, index) in dataList" :key"index":style"{width: calc(100% - ${(index 1) * 10}px)}"c…...

编程日记 2023/10/15 14:51:14

I2VGen-XL高清图像生成视频大模型

本项目I2VGen-XL旨在解决根据输入图像生成高清视频任务。I2VGen-XL由达摩院研发的高清视频生成基础模型之一&#xff0c;其核心部分包含两个阶段&#xff0c;分别解决语义一致性和清晰度的问题&#xff0c;参数量共计约37亿&#xff0c;模型经过在大规模视频和图像数据混合预训…...

编程日记 2023/10/15 14:50:12

Angular知识点系列（1）-每天10个小知识

目录 1. Angular工作原理和与其他前端框架的区别2. 使用Angular的经验和最喜欢的特性3. 使用的最复杂的Angular组件或指令4. Angular的依赖注入系统和示例5. Angular的模块和组件生命周期6. 使用Angular路由和路由保护7. 在Angular应用中实现延迟加载8. 处理Angular应用中的状态…...

编程日记 2023/10/15 14:49:11

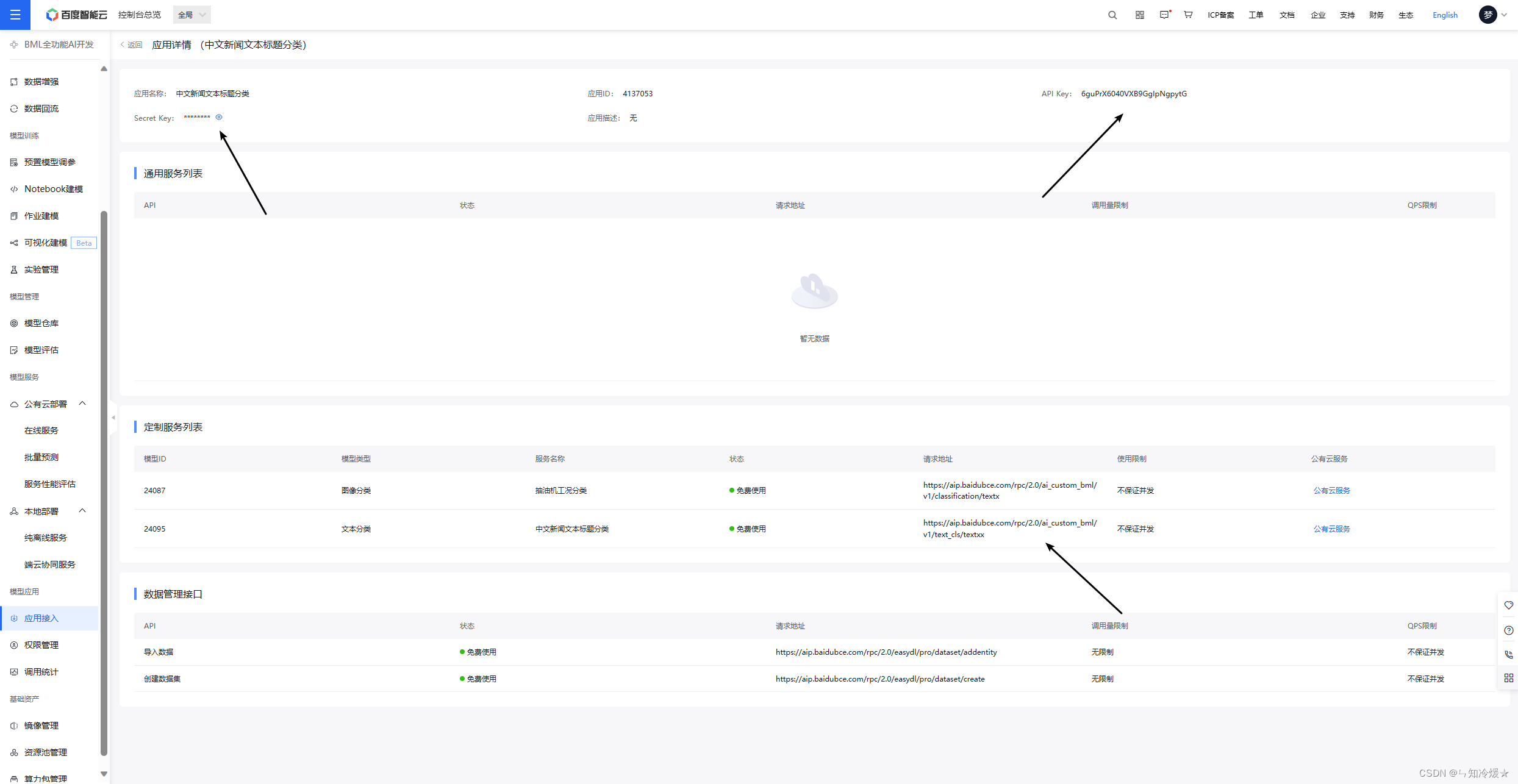
【从0开发】百度BML全功能AI开发平台【实操：以部署情感分析模型为例】

目录 一、全功能AI开发平台介绍二、AI项目落地应用流程&#xff08;以文本分类为例&#xff09;2-0、项目开始2-1、项目背景2-2、数据准备介绍2-3、项目数据2-4、建模调参介绍2-5、项目的建模调参2-6、开发部署2-7、项目在公有云的部署 附录&#xff1a;调用api代码总结 一、全…...

编程日记 2023/10/15 14:48:10

源码解析FlinkKafkaConsumer支持punctuated水位线发送

背景 FlinkKafkaConsumer支持当收到某个kafka分区中的某条记录时发送水位线&#xff0c;比如这条特殊的记录代表一个完整记录的结束等&#xff0c;本文就来解析下发送punctuated水位线的源码 punctuated 水位线发送源码解析 1.首先KafkaFetcher中的runFetchLoop方法 public…...

编程日记 2023/10/15 14:47:10

vue3学习（五）--- 父子组件传值

文章目录 defineProps普通写法TS写法 defineEmits普通写法TS写法 defineExpose defineProps 和 defineEmits 都是只能在 <script setup> 中使用的编译器宏。他们不需要导入&#xff0c;且会随着 <script setup> 的处理过程一同被编译掉。 defineProps 接收父组件传…...

编程日记 2023/10/15 14:46:08

寻找AI时代的关键拼图，从美国橡树岭国家实验室读懂AI存力信标

超算&#xff0c;是计算产业的明珠&#xff0c;是人类探索未知的航船。超算的发展与变化&#xff0c;不仅代表着各个国家与地区间的科技竞争力&#xff0c;更将作为趋势风向标&#xff0c;影响整个数字化体系的走向。 在目前阶段&#xff0c;超算与AI计算的融合是大势所趋。为了…...

编程日记 2023/10/15 14:45:07

多线程并发篇---第十二篇

系列文章目录 文章目录 系列文章目录一、说说ThreadLocal原理？二、线程池原理知道吗？以及核心参数三、线程池的拒绝策略有哪些？一、说说ThreadLocal原理？ hreadLocal可以理解为线程本地变量，他会在每个线程都创建一个副本，那么在线程之间访问内部 副本变量就行了，做到了…...

编程日记 2023/10/15 14:44:06

P7537 [COCI2016-2017#4] Rima

由于题目涉及到后缀&#xff0c;不难想到用 trie 树处理。 将每个字符串翻转插入 trie&#xff0c;后缀就变成了前缀&#xff0c;方便处理。 条件 LCS ( A , B ) ≥ max ⁡ ( ∣ A ∣ , ∣ B ∣ ) − 1 \text{LCS}(A,B) \ge \max(|A|,|B|)-1 LCS(A,B)≥max(∣A∣,∣B∣)−1&…...

编程日记 2023/10/15 14:43:05

SwiftUI Swift CoreData 计算某实体某属性总和

有一个名为 Item 的实体&#xff0c;它有一个名为 amount 的 Double 属性&#xff0c;向你的 View 添加一个计算属性&#xff1a; Code: struct ContentView: View {Environment(\.managedObjectContext) private var viewContextFetchRequest(sortDescriptors: [NSSortDescri…...

编程日记 2023/10/15 14:42:04

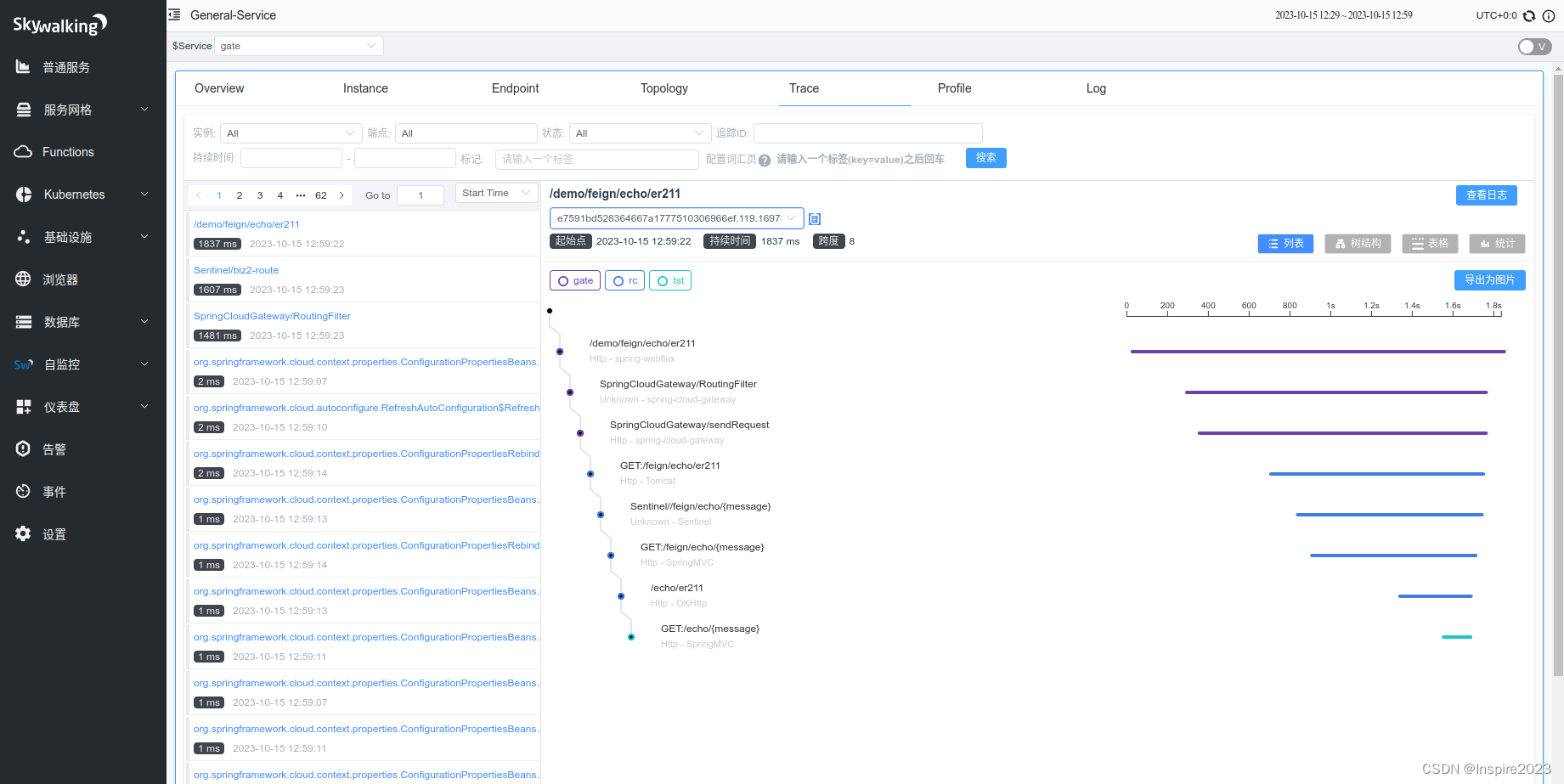
docker安装skyWalking笔记

确保安装了docker和docker-compose sudo docker -v Docker version 20.10.12, build 20.10.12-0ubuntu4 sudo docker-compose -v docker-compose version 1.29.2, build unknown 编写docker-compose.yml version: "3.1" services: skywalking-oap:image: apach…...

编程日记 2023/10/15 14:41:02

【Codeforces】 CF1097G Vladislav and a Great Legend

题目链接 CF方向 Luogu方向 题目解法 首先一个套路是普通幂转下降幂&#xff08;为什么&#xff1f;因为观察到 k k k 很小&#xff0c;下降幂可以转化组合数问题&#xff0c;从而 d p dp dp 求解&#xff09; 即 f ( X ) k ∑ i 0 k { k i } i ! ( f ( X ) i ) f(X)^k…...

编程日记 2023/10/15 14:40:01

力扣每日一题36：有效的数独

题目描述&#xff1a; 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 &#xff0c;验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#xff08;请参考…...

编程日记 2023/10/15 14:38:59

钉钉数字校园小程序开发：开启智慧教育新时代

随着信息技术的快速发展和校园管理的日益复杂化&#xff0c;数字校园已成为现代教育的重要趋势。钉钉数字校园小程序作为一种创新应用&#xff0c;以其专业性、思考深度和逻辑性&#xff0c;为学校提供了全新的管理、教学和沟方式。本文从需求分析、技术实现和应用思考三个方面…...

编程日记 2023/10/15 14:37:57

FFmpeg 低延迟同屏方案

引言 在实时互动需求激增的当下&#xff0c;无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作&#xff0c;还是游戏直播的画面实时传输&#xff0c;低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架&#xff0c;凭借其灵活的编解码、数据…...

编程新知 2025/11/4 6:26:59

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

【磁盘】每天掌握一个Linux命令 - iostat

目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat&#xff08;I/O Statistics&#xff09;是Linux系统下用于监视系统输入输出设备和CPU使…...

编程新知 2025/9/30 16:39:11

ArcGIS Pro制作水平横向图例+多级标注

今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作&#xff1a;ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等&#xff08;ArcGIS出图图例8大技巧&#xff09;&#xff0c;那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

编程新知 2026/2/4 17:18:03

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2026/1/31 13:13:32

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体&#xff08;对象或容器&#xff09;QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质&#xff08;定义颜色、反光等&#xff09;QFirstPersonC…...

编程新知 2026/1/29 5:26:37

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2026/1/30 3:27:35

MySQL 索引底层结构揭秘：B-Tree 与 B+Tree 的区别与应用

文章目录 一、背景知识&#xff1a;什么是 B-Tree 和 BTree&#xff1f; B-Tree&#xff08;平衡多路查找树&#xff09; BTree&#xff08;B-Tree 的变种&#xff09; 二、结构对比&#xff1a;一张图看懂 三、为什么 MySQL InnoDB 选择 BTree&#xff1f; 1. 范围查询更快 2…...

编程新知 2026/2/3 19:38:38

【LeetCode】算法详解#6 ---除自身以外数组的乘积

1.题目介绍 给定一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O…...

编程新知 2026/2/9 9:22:40

数学建模-滑翔伞伞翼面积的设计，运动状态计算和优化 ！

我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态，并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

编程新知 2026/2/6 5:55:05