P4451 [国家集训队] 整数的lqp拆分
传送门:洛谷
解题思路:
考虑设 f ( i ) f(i) f(i)为和为 i i i的拆分权值和,那么我们可以得到一个递推关系式 f ( i ) = ∑ i = 1 n f ( n − i ) ∗ f i b ( i ) f(i)=\sum_{i=1}^nf(n-i)*fib(i) f(i)=i=1∑nf(n−i)∗fib(i)这个表达式的含义就是枚举一个数的值,由于分配率,我们给每一个和乘上一个数,相当于给整体乘上一个数
此时我们发现, f ( 0 ) f(0) f(0)应该为 1 1 1,但是光光的由上面的式子,我们并不能得到 f ( 0 ) f(0) f(0)为1,所以我们考虑补充定义 f ( 0 ) = 1 f(0)=1 f(0)=1
也就是说此时 f ( i ) = [ n = 1 ] + ∑ i = 1 n f ( n − i ) ∗ f i b ( i ) f(i)=[n=1]+\sum_{i=1}^nf(n-i)*fib(i) f(i)=[n=1]+i=1∑nf(n−i)∗fib(i)
发现很像一个卷积式子,但是下标不为 1 1 1,因为 f i b ( 0 ) = 0 fib(0)=0 fib(0)=0(这意味着常数项一定为0,不会影响 f ( 0 ) f(0) f(0)的值),所以我们不妨考虑临时扩展上述式子,可以得到:
f ( i ) = [ n = 1 ] + ∑ i = 0 n f ( n − i ) ∗ f i b ( i ) f(i)=[n=1]+\sum_{i=0}^nf(n-i)*fib(i) f(i)=[n=1]+i=0∑nf(n−i)∗fib(i)
所以我们可以得到, F = F ∗ F I B + 1 F=F*FIB+1 F=F∗FIB+1
化解一下可以得到 F = 1 1 − F I B F=\frac{1}{1-FIB} F=1−FIB1,对于 F I B FIB FIB数列,我们有一个生成函数的结论(限于篇幅,此处不证)
F I B = x 1 − x − x 2 FIB=\frac{x}{1-x-x^2} FIB=1−x−x2x
所以此时我们可以很轻易的写出 F F F的生成函数, F = 1 + x 1 − 2 ∗ x − x 2 F=1+\frac{x}{1-2*x-x^2} F=1+1−2∗x−x2x
我们现在需要做的事就是将 F F F展开回去,因为 F [ 1 ] = 1 F[1]=1 F[1]=1,所以1可以直接分开拿出来,现在考虑后面的那一个分式.
根据套路,这应该是一个可以裂项的式子,考虑待定系数法来裂项,
我们可以得到 x 1 − 2 ∗ x − x 2 = 2 4 ∗ ( 1 1 − ( 1 + 2 ) x − 1 1 − ( 1 − 2 ) x ) \frac{x}{1-2*x-x^2}=\frac{\sqrt{2}}{4}*(\frac{1}{1-(1+\sqrt{2})x}-\frac{1}{1-(1-\sqrt{2})x}) 1−2∗x−x2x=42∗(1−(1+2)x1−1−(1−2)x1)
根据一些生成函数的小结论, ∑ i = 0 ∞ x i = 1 1 − x \sum_{i=0}^{\infty}x^i=\frac{1}{1-x} ∑i=0∞xi=1−x1
我们对上述式子进行展开,可以得到:
F = 1 ∗ x 0 + 2 4 ∗ ∑ i = 0 ∞ ( ( 1 + 2 ) i − ( 1 − 2 ) i ) x i F=1*x^0+\frac{\sqrt{2}}{4}*\sum_{i=0}^\infty((1+\sqrt{2})^i-(1-\sqrt{2})^i)x^i F=1∗x0+42∗i=0∑∞((1+2)i−(1−2)i)xi
不难看出,我们最终的答案就是 ( 1 + 2 ) i − ( 1 − 2 ) i (1+\sqrt{2})^i-(1-\sqrt{2})^i (1+2)i−(1−2)i
此时还需要考虑 2 \sqrt{2} 2的二次剩余,也就是考虑这样的一个同余方程:
x 2 ≡ 2 m o d p x^2\equiv2\;mod\;p x2≡2modp
因为我们现在并不是解决二次剩余问题,我们只需要求出一个数的二次剩余,所以我们大可以在本地跑出这个式子的答案.
至此,本题解决.
下面是本题的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const int mod=1e9+7;
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int qpow(int a,int b) {int ans=1;while(b) {if(b&1) ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans;
}
int sqrt2=59713600;
void init() {for(int i=1;i<=mod;i++) {if(i*i%mod==2) {sqrt2=i;break;}}
}
signed main() {int n=0;string s;cin>>s;for(int i=0;i<s.length();i++) n=(n*10+s[i]-'0')%(mod-1);
// init();cout<<(qpow(1+sqrt2,n)-qpow((1-sqrt2+mod)%mod,n)%mod+mod)%mod*qpow(2*sqrt2%mod,mod-2)%mod<<endl;return 0;
}
相关文章:

P4451 [国家集训队] 整数的lqp拆分
传送门:洛谷 解题思路: 考虑设 f ( i ) f(i) f(i)为和为 i i i的拆分权值和,那么我们可以得到一个递推关系式 f ( i ) ∑ i 1 n f ( n − i ) ∗ f i b ( i ) f(i)\sum_{i1}^nf(n-i)*fib(i) f(i)i1∑nf(n−i)∗fib(i)这个表达式的含义就是枚举一个数的值,由于分配率,我们…...

Mysql 日常命令记录
索引操作 加联合组件: ALTER TABLE dws_stock_age_material_transactions_total_pri_rpt_update ADD INDEX index_sio (organization_id(16),item_code,subinventory_code); 查看索引: SHOW INDEX FROM dws_stock_age_material_transactions_detail_…...

可视化上证50结构图
可视化上证50结构图 缘由收集数据先获取50支成分股列表获取各成分股票K线数据 数据处理找出来,再删除,然后重新下载数据最终获得每日报价的变化值 图形结构处理聚类分析使用affinity_propagation(亲和传播)聚类 嵌入二维平面空间可视化小结热力图 缘由 …...

STM32_PID通用算法增量式和位置式
STM32_PID通用算法增量式和位置式 前言: 此算法为入门级PID算法,调试好参数后可应用于温度控制、舵机控制、直流电机的转速控制和直流电机的角度控制等等,下面就以温度控制举例 pid.c #include "pid.h" #include "sensor.h&q…...

Spark的数据输入、数据计算、数据输出
PySpark的编程,主要氛围三大步骤:1)数据输入、2)数据处理计算、3)数据输出 1)数据输入:通过SparkContext对象,晚上数据输入 2)数据处理计算:输入数据后得到RDD对象,对RDD…...
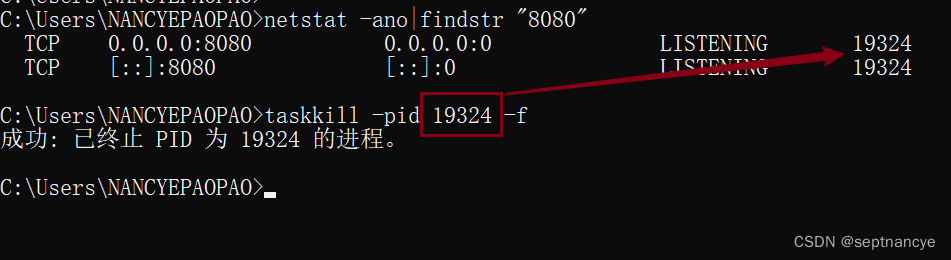
Windows端口号被占用的查看方法及解决办法
Windows端口号被占用的查看方法及解决办法 Error starting ApplicationContext. To display the conditions report re-run your application with debug enabled. 2023-10-14 22:58:32.069 ERROR 6488 --- [ main] o.s.b.d.LoggingFailureAnalysisReporter : ***…...
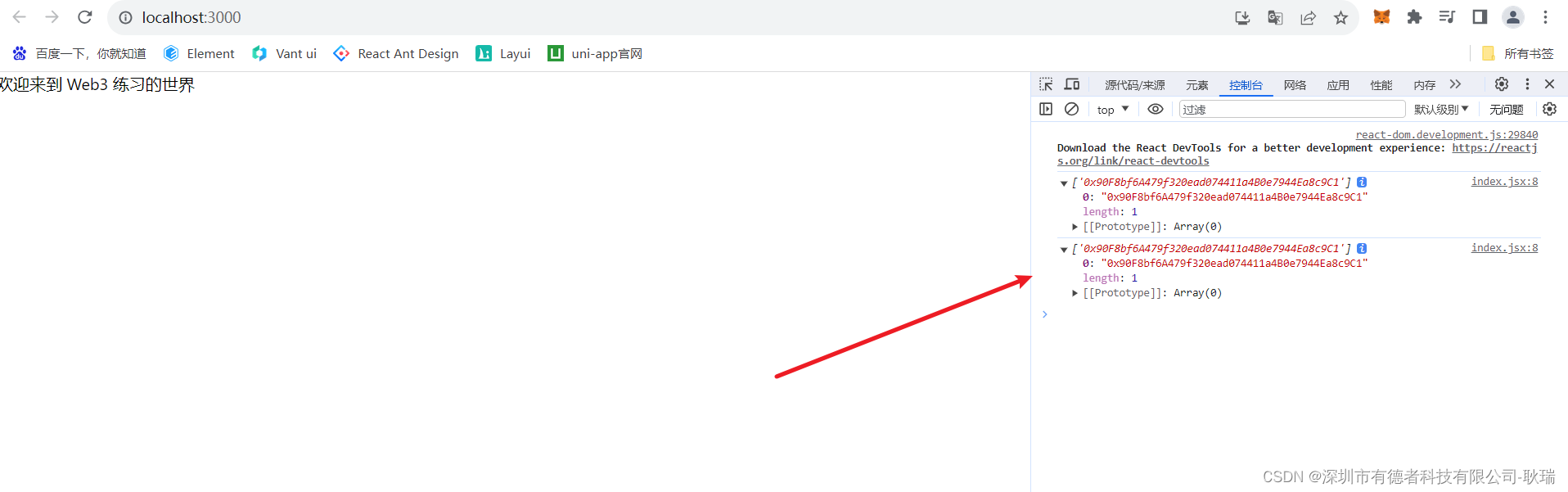
Web3 整理React项目 导入Web3 并获取区块链信息
上文 WEB3 创建React前端Dapp环境并整合solidity项目,融合项目结构便捷前端拿取合约 Abi 我们用react 创建了一个 dapp 项目 并将前后端代码做了个整合 那么 我们就来好好整理一下 我们的前端react的项目结构 我们在 src 目录下创建一个 components 用来存放我们的…...

基于SpringBoot的旅游网站开题报告
一、选题背景 随着旅游业的蓬勃发展和人们对旅游需求的增长,开发一个基于Spring Boot的旅游网站具有重要的意义。传统的旅行社模式逐渐不能满足人们个性化、多样化的旅游需求,因此开发一个在线旅游网站能够为用户提供更加便捷、灵活、个性化的旅游服务&…...
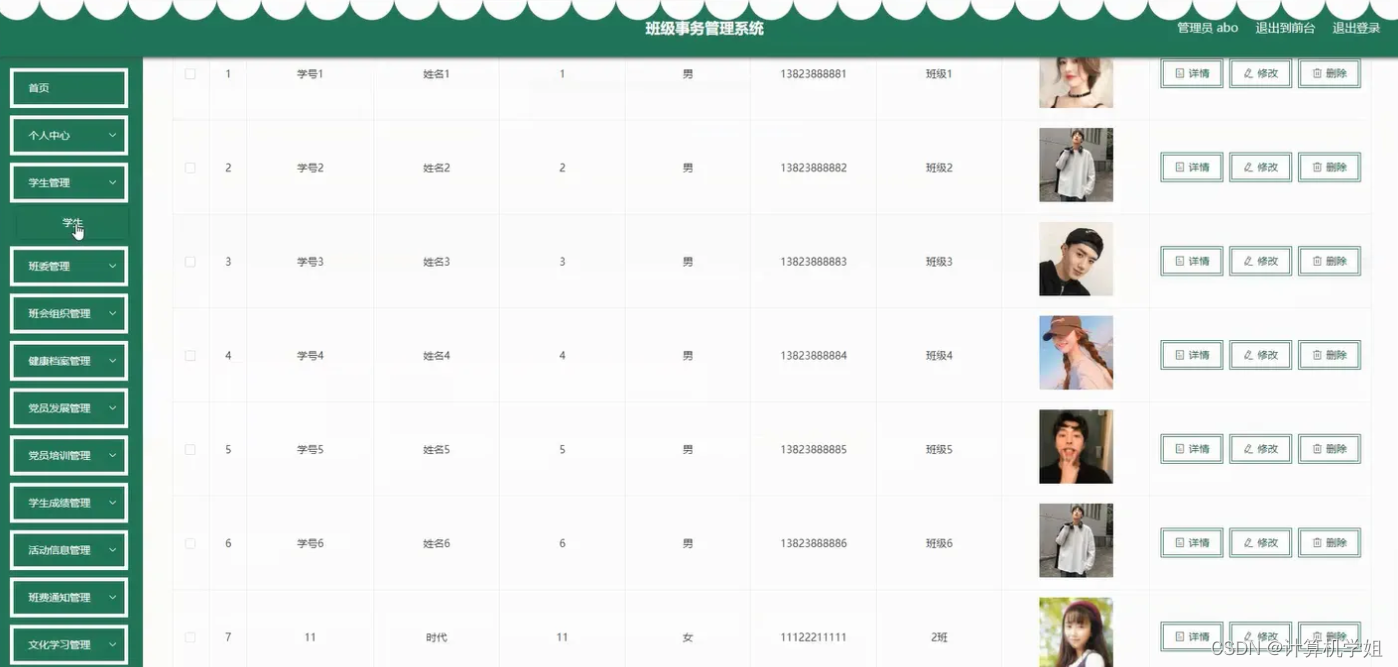
基于SSM的班级事务管理系统
基于SSM的班级事务管理系统 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 前台界面 登录界面 班委界面 学生界面 管理员界面 摘要 基于SSM(Spring、Spring…...

基于Spring Boot开发的汽车租赁管理系统
文章目录 项目介绍主要功能截图:后台前台部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于Spring Boot开发的汽车租赁…...
精品基于django的高校竞赛比赛管理系统Python
《[含文档PPT源码等]精品基于django的高校竞赛管理系统》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程等! 软件开发环境及开发工具: 开发语言:python 使用框架:Django 前端技术:JavaScri…...

RustDay04------Exercise[01-10]
1.做题须知 这一题告诉我们可以尝试修改下面的输出,在觉得OK之后删除// I AM NOT DONE注释即可进入下一题 // intro1.rs // About this I AM NOT DONE thing: // We sometimes encourage you to keep trying things on a given exercise, even // after you already figured …...
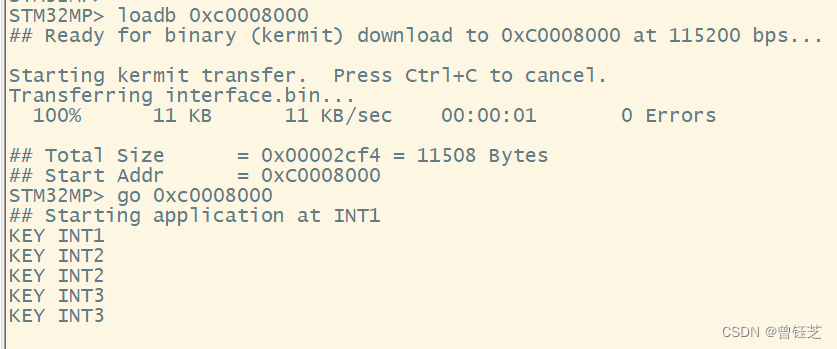
ARM day9
src/key_it.c #include "key_it.h" #include "led.h" void key_it_config() {//RCC使能GPIOF时钟RCC->MP_AHB4ENSETR | (0x1<<5);//设置PF9 PF7 PF8GPIO输入//PF9GPIOF->MODER & (~(0x3<<18));//PF8GPIOF->MODER & (~(0x3&l…...

【TensorFlow2 之013】TensorFlow-Lite
一、说明 在这篇文章中,我们将展示如何构建计算机视觉模型并准备将其部署在移动和嵌入式设备上。有了这些知识,您就可以真正将脚本部署到日常使用或移动应用程序中。 教程概述: 介绍在 TensorFlow 中构建模型将模型转换为 TensorFlow Lite训练…...

Java基础--阳光总在风雨后,请相信彩虹
1、今日任务 JAVA SE-韩顺平视频教程–30p以上(今天得50p以上因为是基础)计算机基础八股记忆总结刷题(两题)可以先用python 1、SSM ssm->Spring(轻量级的文本开发框架)/SpringMVC(分层的w…...

高级网络调试技巧:使用Charles Proxy捕获和修改HTTP/HTTPS请求
今天我将与大家分享一种强大的网络调试技巧,那就是使用Charles Proxy来捕获和修改HTTP/HTTPS请求。如果您是一位开发人员或者网络调试爱好者,那么这个工具肯定对您有着很大的帮助。接下来,让我们一起来学习如何使用Charles Proxy进行高级网络…...
Discuz大气游戏风格模板/仿lol英雄联盟游戏DZ游戏模板GBK
Discuz大气游戏风格模板,lol英雄联盟游戏模板,DZ游戏娱乐模板GBK。模板名称:lol英雄联盟游戏(m0398_lol) 下载地址:https://bbs.csdn.net/topics/617408069...
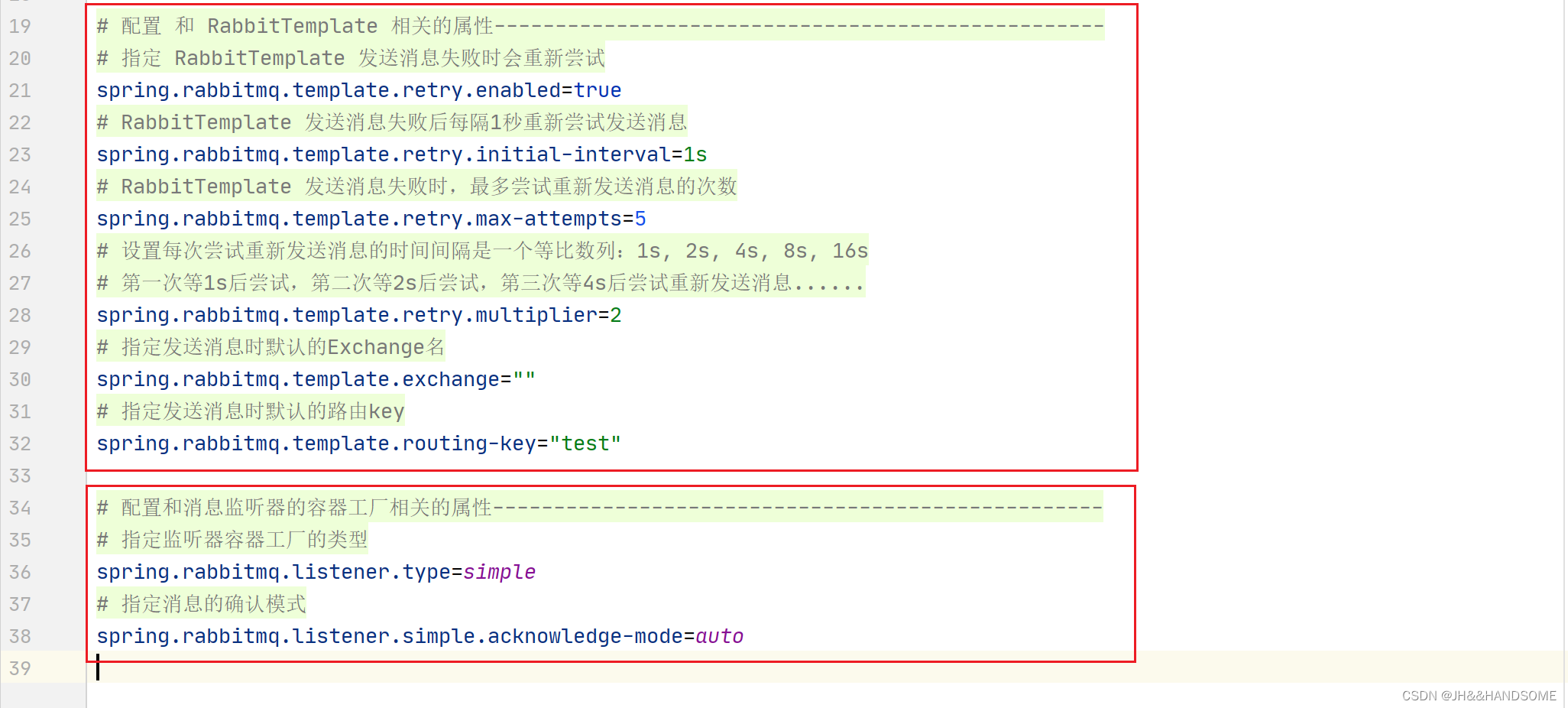
206、SpringBoot 整合 RabbitMQ 的自动配置类 和 对应的属性处理类 的知识点
目录 ★ Spring Boot 为 RabbitMQ 提供的自动配置▲ 自动配置类:RabbitAutoConfiguration▲ 属性处理类:RabbitProperties相关配置 ★ AmqpAdmin的方法★ AmqpTemplate的方法代码演示创建一个springboot的项目。application.properties 配置属性 ★ Spri…...
网络链接失败怀疑是服务器处于非正常状态?如何用本地电脑查看服务器是否正常?
网络链接失败怀疑是服务器处于非正常状态?如何用本地电脑查看服务器是否正常? 网页会出现链接失败,可以实时用cdm大法,cdm可以更好的排查字节数据的返回,可以让我们更好的要检查服务器是否处于正常状态,接下…...

文件操作(打开关闭文件、文件顺序以及随机读写)
文章目录 写在前面1. 文件的打开与关闭1.1 文件指针1.2 文件的打开(fopen)与关闭(fclose)1.2.1 fopen函数1.2.2 fclose函数 2. 文件的顺序读写2.1. fgetc 和 fputc函数2.1.1 fputc函数2.1.2 fgetc函数 2.2 fgets 和 fputs函数2.2.1 fputs函数2.2.2 fgets函数 2.3 fscanf和fprin…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
