时间复杂度为 O(n^2) 的排序算法
大家好,我是 方圆。对于小规模数据,我们可以选用时间复杂度为 O(n2) 的排序算法,因为时间复杂度并不代表实际代码的执行时间,而且它也省去了低阶、系数和常数,仅代表的增长趋势,所以在小规模数据情况下, O(n2) 的排序算法可能会比 O(nlogn) 的排序算法执行效率高。不过随着数据规模增大, O(nlogn) 的排序算法是不二选择。本篇我们主要对 O(n2) 的排序算法进行介绍,在介绍之前,我们先了解一下算法特性:
-
算法特性:
-
稳定性:经排序后,若等值元素之间的相对位置不变则为稳定排序算法,否则为不稳定排序算法
-
原地排序:是否借助额外辅助空间
-
自适应性: 自适应性排序受输入数据的影响,即最佳/平均/最差时间复杂度不等,而非自适应排序时间复杂度恒定
-
本篇我们将着重介绍插入排序,选择排序和冒泡排序了解即可。
插入排序
插入排序的工作方式像 整理手中的扑克牌一样,即不断地将每一张牌插入到其他已经有序的牌中适当的位置。
插入排序的当前索引元素左侧的所有元素都是有序的:若当前索引为 i,则 [0, i - 1] 区间内的元素始终有序,这种性质被称为 循环不变式,即在第一次迭代、迭代过程中和迭代结束时,这种性质始终保持不变。
不过,这些有序元素的索引位置暂时不能确定,因为它们可能需要为更小的元素腾出空间而向右移动。插入排序的代码实现如下:
private void sort(int[] nums) {for (int i = 1; i < nums.length; i++) {int base = nums[i];int j = i - 1;while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j--];}nums[j + 1] = base;}}
它的实现逻辑是取未排序区间中的某个元素为基准数 base,将 base 与其左侧已排序区间元素依次比较大小,并"插入"到正确位置。插入排序对 部分有序(数组中每个元素距离它的最终位置都不远或数组中只有几个元素的位置不正确等情况)的数组排序效率很高。事实上,当逆序很少或数据量不大(n2和nlogn比较接近)时,插入排序可能比其他任何排序算法都要快,这也是一些编程语言的内置排序算法在针对小数据量数据排序时选择使用插入排序的原因。
算法特性:
-
空间复杂度:O(1)
-
原地排序
-
稳定排序
-
自适应排序:当数组为升序时,时间复杂度为 O(n);当数组为降序时,时间复杂度为 O(n2)
希尔排序
插入排序对于大规模乱序数组排序很慢,因为它只会交换相邻的元素,所以元素只能一步步地从一端移动到另一端,如果最小的元素恰好在数组的最右端,要将它移动到正确的位置需要移动 N - 1 次。
希尔排序是基于插入排序改进的排序算法,它可以交换不相邻的元素以对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。它的思想是使数组中间隔为 h 的元素有序(h 有序数组),如下图为间隔为 4 的有序数组:
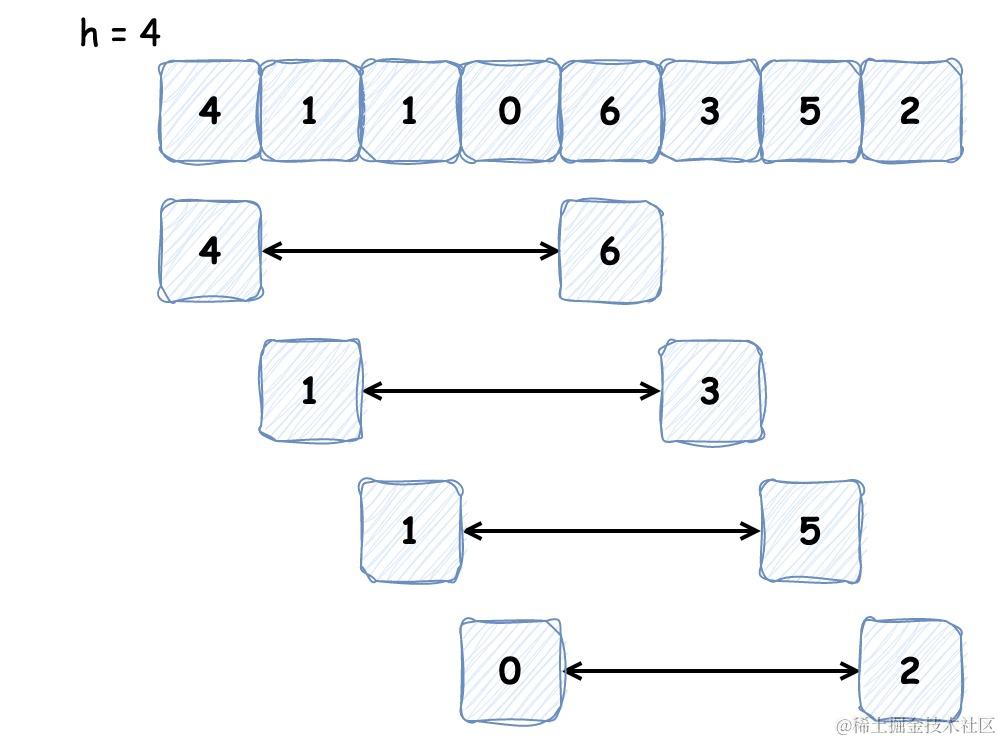
排序之初 h 较大,这样我们能将较小的元素尽可能移动到靠近左端的位置,为实现更小的 h 有序创造便利,最后一次循环时 h 为 1,便是我们熟悉的插入排序。这就是希尔排序的过程,代码实现如下:
private void sort(int[] nums) {int N = nums.length;int h = 1;while (h < N / 3) {h = 3 * h + 1;}while (h >= 1) {for (int i = h; i < N; i++) {int base = nums[i];int j = i - h;while (j >= 0 && nums[j] > base) {nums[j + h] = nums[j];j -= h;}nums[j + h] = base;}h /= 3;}}
希尔排序更高效的原因是它权衡了子数组的规模和有序性,它也可以用于大型数组。排序之初,各个子数组都很短,排序之后子数组都是部分有序的,这两种情况都很适合插入排序。
选择排序
选择排序的实现非常简单:每次选择未排序数组中的最小值,将其放到已排序区间的末尾,代码实现如下:
private void sort(int[] nums) {for (int i = 0; i < nums.length; i++) {int min = i;for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[min]) {min = j;}}swap(nums, i, min);}}private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
算法特性:
-
空间复杂度:O(1)
-
原地排序
-
非稳定排序:会改变等值元素之间的相对位置
-
非自适应排序:最好/平均/最坏时间复杂度均为 O(n2)
冒泡排序
冒泡排序通过 连续地比较与交换相邻元素实现排序,每轮循环会将未被排序区间内的最大值移动到数组的最右端,这个过程就像是气泡从底部升到顶部一样,代码实现如下:
public void sort(int[] nums) {for (int i = nums.length - 1; i > 0; i--) {// 没有发生元素交换的标志位boolean flag = true;for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {swap(nums, j, j + 1);flag = false;}}if (flag) {break;}}}private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
算法特性:
-
空间复杂度:O(1)
-
原地排序
-
稳定排序
-
自适应排序:经过优化后最佳时间复杂度为 O(n)
巨人的肩膀
-
《算法导论 第三版》第 2.1 章
-
《算法 第四版》第 2.1 章
-
《Hello 算法》第 11 章
-
排序算法-希尔排序
相关文章:

时间复杂度为 O(n^2) 的排序算法
大家好,我是 方圆。对于小规模数据,我们可以选用时间复杂度为 O(n2) 的排序算法,因为时间复杂度并不代表实际代码的执行时间,而且它也省去了低阶、系数和常数,仅代表的增长趋势,所以在小规模数据情况下&…...

ES6 Map数据结构
1.Map是什么? ES6 提供的另一种新的引用类型的数据结构 它类似于对象,也是键值对的集合,但是“键”的范围不限于字符串,各种类型的值(包括对象)都可以当作键) 以前引用类型中的对象也是键值对…...

网页数据采集HTTP Get,Post登录提交数据--VBS之Microsoft.XMLHTTP对象
MSXML中提供了Microsoft.XMLHTTP对象,能够完成从数据包到Request对象的转换以及发送任务。 创建XMLHTTP对象的语句如下: Set objXML CreateObject("Msxml2.XMLHTTP") 或 Set objXML CreateObject(“Microsoft.XMLHTTP”) Or, for version 3…...

强化科技创新“辐射力”,中国移动的数智化大棋局
作者 | 曾响铃 文 | 响铃说 丝滑流畅的5G连接、每时每刻的数字生活服务、无处不在的智能终端、拟人交流的AI助手、梦幻般的XR虚拟现实、直接感受的裸眼3D…… 不知不觉,那个科幻片中的世界,越来越近。 数智化新世界的“气氛”,由一个个具…...

喜报 | 擎创科技实力亮相2023科创会并荣获科技创新奖
近日,由国家互联网数据中心产业技术创新战略联盟(NIISA)主办的“2023第二届国际互联网产业科技创新大会暨互联网创新产品展览会”于北京圆满落幕。 擎创科技副总裁冯陈湧受邀出席本次论坛,并发表了“银行分布式核心智能运维体系思…...
--- keep-alive缓存组件)
vue3学习(九)--- keep-alive缓存组件
有时候我们不希望组件被重新渲染影响使用体验;或者处于性能考虑,避免多次重复渲染降低性能。而是希望组件可以缓存下来,维持当前的状态。这时候就需要用到keep-alive组件。 keep-alive有两个独有的生命周期:activated、 deactivated 接下来看…...

用servlet实现一个简单的猜数字游戏。
需要两个页面,一个jsp页面(guess.jsp)和servlet页面(servlet)。 一.jsp页面 在jsp页面中需要实现: 1.创建随机数并且保存在session中。 2.做个form表单提交猜的数字给servlet页面。 <%page import&…...

前端取消请求
取消请求 发送一个异步请求获取数据,并在控制台中打印出返回结果。这里使用了 fetch 方法来发送请求,同时使用 AbortController 对象来实现请求的取消操作。 具体来说,代码中定义了一个 list 函数,该函数会创建一个 AbortContro…...

关于6轴球腕机械臂的肩部奇异描述纠正
对于常见的球腕6轴机械臂构型,在大多数资料中奇异点描述如下: 肩部奇异点(Shoulder singularity): 肩部奇异点是在机器人手腕的中心与J1轴关节在同一条直线上时发生。这种情况下,会导致关节轴1和4试图瞬间旋…...

Python —— hou.Node class
Houdini内所有节点(Object、SOP、COP等)的基类,该类的实例对应houdini内的节点; 每个节点都有一个唯一的路径(定义其在节点树内的位置);节点路径层次结构类似于文件系统中的文件和文件夹的层次结…...
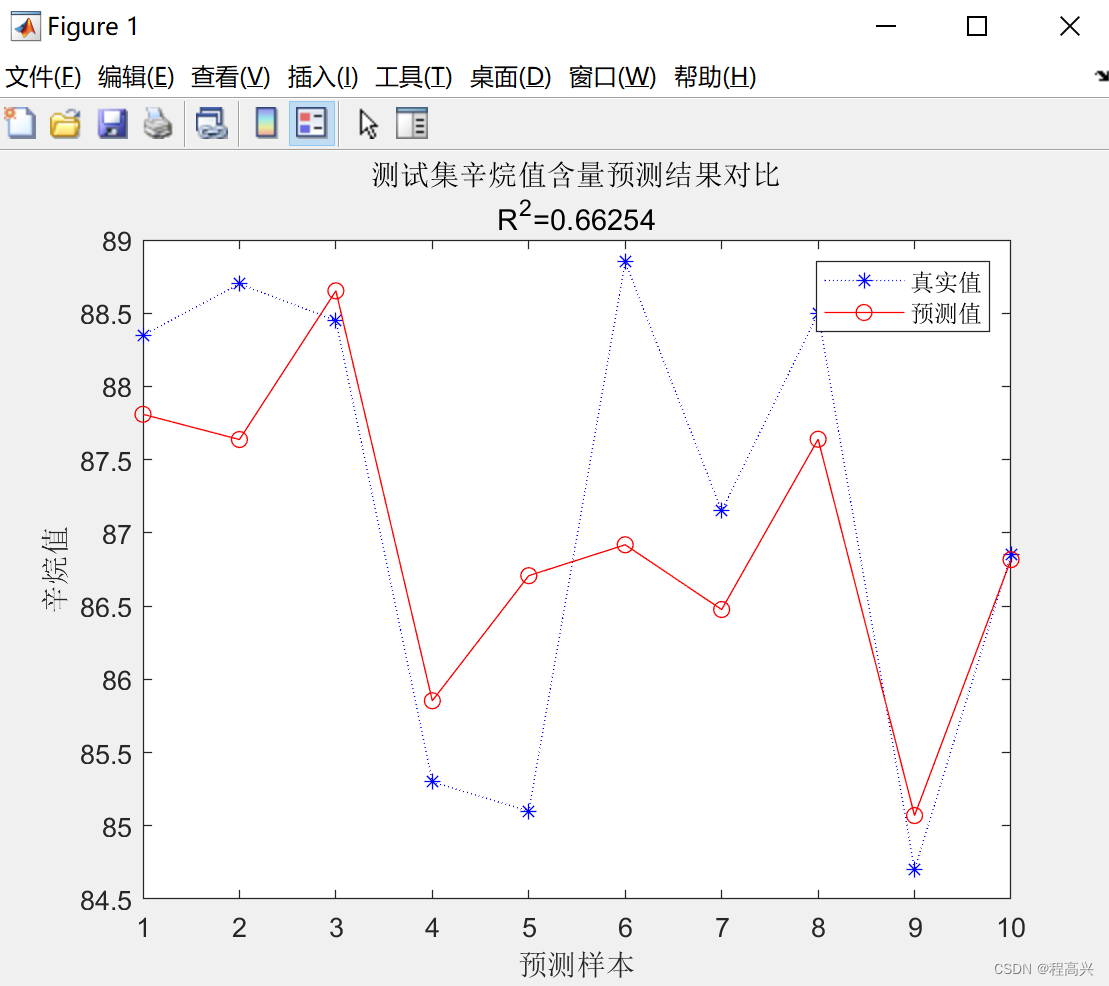
MATLAB——RBF、GRNN和PNN神经网络案例参考程序
欢迎关注“电击小子程高兴的MATLAB小屋” %————RBF程序实例 %% I. 清空环境变量 clear all clc %% II. 训练集/测试集产生 %% % 1. 导入数据 load spectra_data.mat %% % 2. 随机产生训练集和测试集 temp randperm(size(NIR,1)); % 训练集——50个样本 P_train NIR(t…...

E138: Can‘t write viminfo file
E138: Can’t write viminfo file /home/xxx/.viminfo! 原因 进入/home/xxx/目录下,用ls -a你会发现有很多.viminfa.tmp - .viminfz.tmp 这种的临时文件,这是因为使用vim编辑器时,如果编辑器没有正常退出就会生成一个暂存文件,…...
Compose Canvas基础(2) 图形转换
Compose Canvas基础(2)图形转换 前言平移 translate缩放 scale旋转 rotate自定义绘图区域及绘制内边距inset组合转换 withTransform完整代码总结 上一篇文章 Compose Canvas基础(1) drawxxx方法 前言 阅读本文需要一定compose基…...
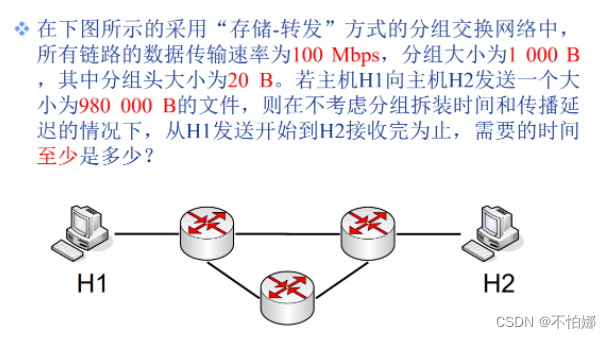
【计算机网络笔记】分组交换中的报文交付时间计算例题
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 系列文章目录题目解答 题目 在下图所示的采用“存储-转发”方式的分组交换网络中所有链路的数据传输速率为100 Mbps,分…...
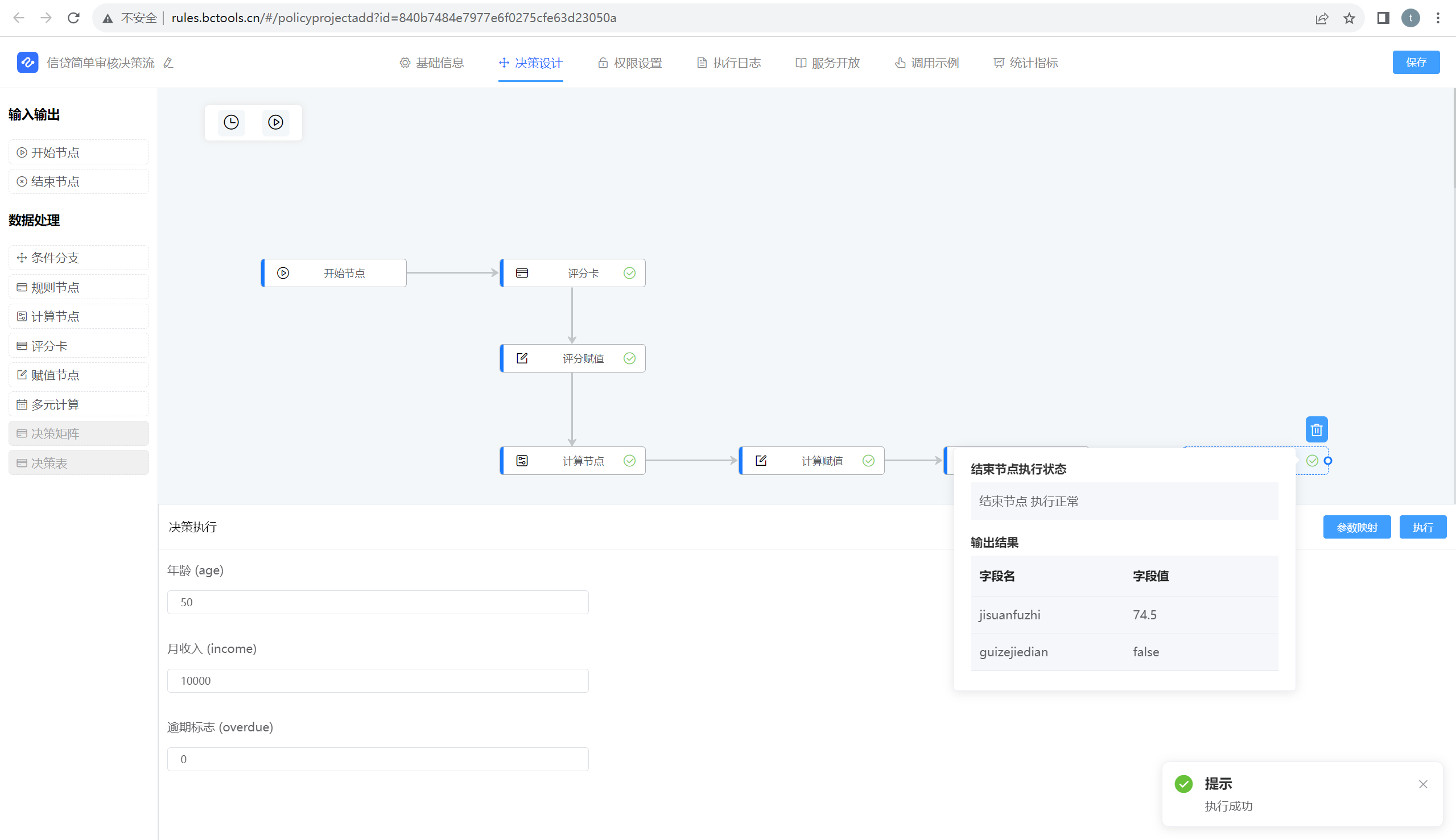
JVS-rules规则引擎,解决大数据风控的自动化决策利器
规则引擎中的评分卡节点是一种用于评估客户信用、风险等级或其他指标的重要工具。它通常用于金融、信贷等领域,以便根据一系列预定义的规则和权重来对客户进行评分。以下是评分卡节点的主要功能、作用以及配置方式的介绍: 功能和作用: 评估…...
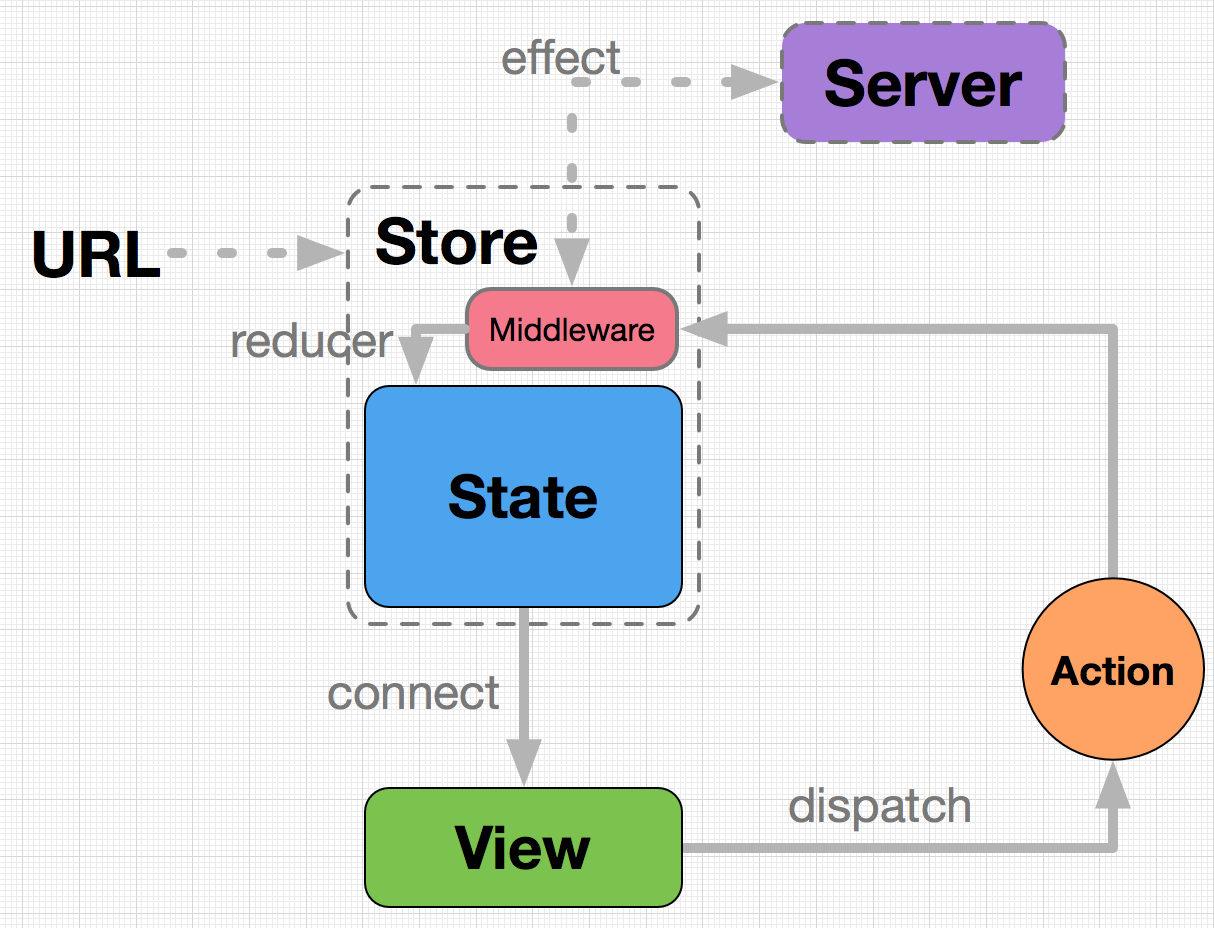
dvaJs在react 项目中的简单使用
官网:入门课 | DvaJS 备注:个人学习 代码示例: getColumns.js const getColumns [{title: 姓名, // 列标题dataIndex: name, // 数据字段名称,与数据中的字段名对应key: name, // 列的唯一键},{title: 年龄, // 列标题dataIn…...

如何将las数据转换为osgb数据?
答:如果是需要用点云建模可使用重建大师。如果只是想转换格式可以使用网格大师的点云转osgb工具。 重建大师是一款专为超大规模实景三维数据生产而设计的集群并行处理软件,输入倾斜照片,激光点云,POS信息及像控点,输出…...

创新与重塑,佛塑科技打造集团型 CRM 建设标杆
“十四五”时期是我国全面建成小康社会、实现第一个百年奋斗目标之后,乘势而上开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的第一个五年。 在政府有序推进“十四五”规划的进程中,佛山佛塑科技集团股份有限公司(证券简…...
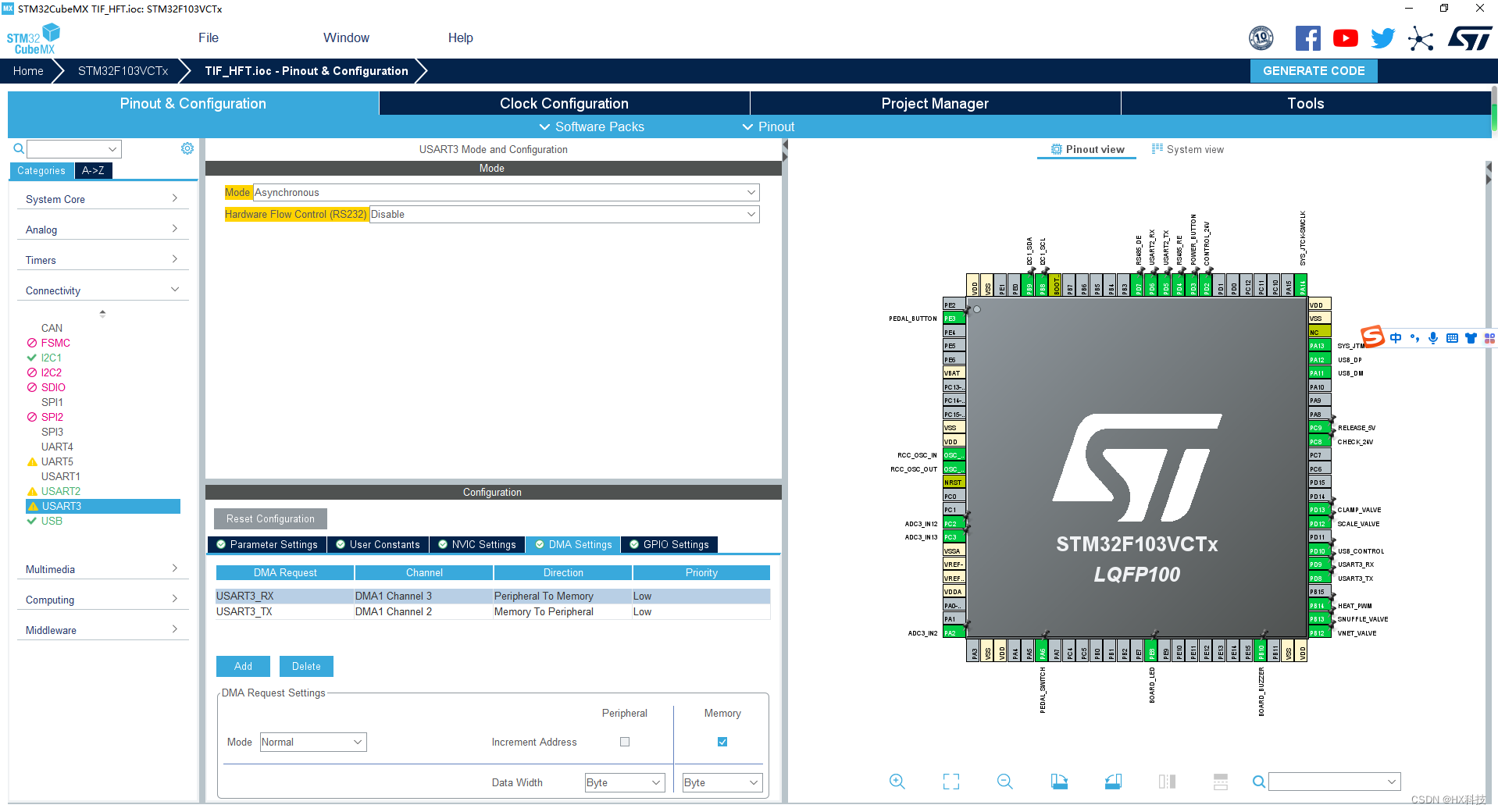
STM32CUBEMX_DMA串口空闲中断接收+接收发送缓冲区
STM32CUBEMX_DMA串口空闲中断接收接收发送缓冲区 前言: 我了解的串口接收指令的方式有:在这里插入图片描述 1、接收数据中断特定帧尾 2、接收数据中断空闲中断 3、DMA接收空闲中断 我最推荐第三种,尤其是数据量比较大且频繁的时候 串口配置 …...
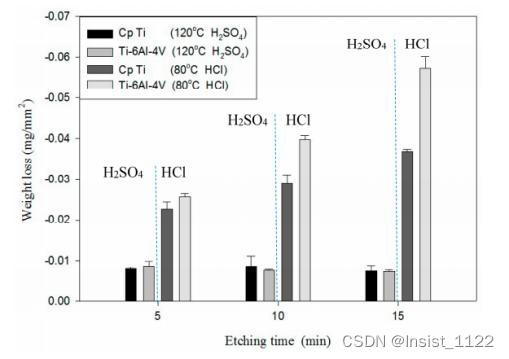
酸蚀刻对钛医药材料纳米形态表面特性及活化能的影响
引言 由于商业纯钛(CP Ti)具有抗腐蚀性,并且具有合适的机械性能以及生物相容性,因此,目前一直被用作牙科植入材料。为了在临床手术中获得高水平的成功,CP Ti的表面质量和形貌是影响植入手术结果的比较关键的因素之一,…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
