AtCoder abc130
F题提交了无数遍,最后发现是三分求解的写法错了
C - Rectangle Cutting
盲猜都在xy的中心点时可以无限分割,否则不能
D - Enough Array
前缀和二分求位置
E - Common Subsequence
公共子序列求有几种组合
设 d p [ i ] [ j ] dp[i][j] dp[i][j]代表s取到i t取到j时的序列数
当s[i]!=t[j] 时
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] − d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i-1] [j] + dp[i][j - 1] - dp[i - 1][j - 1] dp[i][j]=dp[i−1][j]+dp[i][j−1]−dp[i−1][j−1]
因为 d p [ i ] [ j ] dp[i][j] dp[i][j]可以视作为 d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j]添上s[i]后总的序列数
d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]是 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]添上t[j]的序列数
另一边 d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1]也将 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]包含在内,因此计算了两次 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]需要减去
当s[i]==t[j]时, d p [ i ] [ j ] dp[i][j] dp[i][j]在 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]的序列上各增加一个长度,因此在刚才的计算后再加上 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @author : yhdu@tongwoo.cn
# @desc :
# @file : atcoder.py
# @software : PyCharm
import bisect
import copy
import sys
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(100010)mod = 10 ** 9 + 7def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdinn, m = map(int, fp.readline().split())s = list(map(int, fp.readline().split()))t = list(map(int, fp.readline().split()))dp = [[0] * (m + 1) for _ in range(n + 1)]for i in range(n + 1):dp[i][0] = 1for i in range(m + 1):dp[0][i] = 1for i in range(1, n + 1):for j in range(1, m + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]else:dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]dp[i][j] %= modprint(dp[n][m])if __name__ == "__main__":main()F - Minimum Bounding Box
max-min显然是凸函数(忘了证明方法),暴力三分可以过
还有一种不那么暴力的解法:
不需要维护所有的x y
只需要维护向上、向下的y中最大值与最小值
向左向右x最大值与最小值
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @author : yhdu@tongwoo.cn
# @desc :
# @file : atcoder.py
# @software : PyCharm
import bisect
import copy
import sys
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(100010)def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdinn = int(fp.readline())min_x, min_y, max_x, max_y = 10 ** 20, 10 ** 20, -10 ** 20, -10 ** 20uy, dy, lx, rx = [], [], [], []for i in range(n):items = fp.readline().strip().split()x, y = int(items[0]), int(items[1])d = items[2]if d == 'U':uy.append(y)min_x, max_x = min(min_x, x), max(max_x, x)elif d == 'D':dy.append(y)min_x, max_x = min(min_x, x), max(max_x, x)elif d == 'L':lx.append(x)min_y, max_y = min(min_y, y), max(max_y, y)else:rx.append(x)min_y, max_y = min(min_y, y), max(max_y, y)uy.sort()dy.sort()lx.sort()rx.sort()def get(t):x0, y0, x1, y1 = min_x, min_y, max_x, max_yif len(uy) > 0:y0 = min(uy[0] + t, y0)y1 = max(uy[-1] + t, y1)if len(dy) > 0:y0 = min(dy[0] - t, y0)y1 = max(dy[-1] - t, y1)if len(rx) > 0:x0 = min(rx[0] + t, x0)x1 = max(rx[-1] + t, x1)if len(lx) > 0:x0 = min(lx[0] - t, x0)x1 = max(lx[-1] - t, x1)return (y1 - y0) * (x1 - x0)lo, hi = 0, 10 ** 13c = 0ans = 1e18while c < 400:m0, m1 = lo + (hi - lo) / 3, hi - (hi - lo) / 3a0, a1 = get(m0), get(m1)if a0 > a1:lo = m0else:hi = m1ans = min(ans, a0)ans = min(ans, a1)c += 1print(ans)if __name__ == "__main__":main()相关文章:

AtCoder abc130
F题提交了无数遍,最后发现是三分求解的写法错了 C - Rectangle Cutting 盲猜都在xy的中心点时可以无限分割,否则不能 D - Enough Array 前缀和二分求位置 E - Common Subsequence 公共子序列求有几种组合 设 d p [ i ] [ j ] dp[i][j] dp[i][j]代表s取到…...
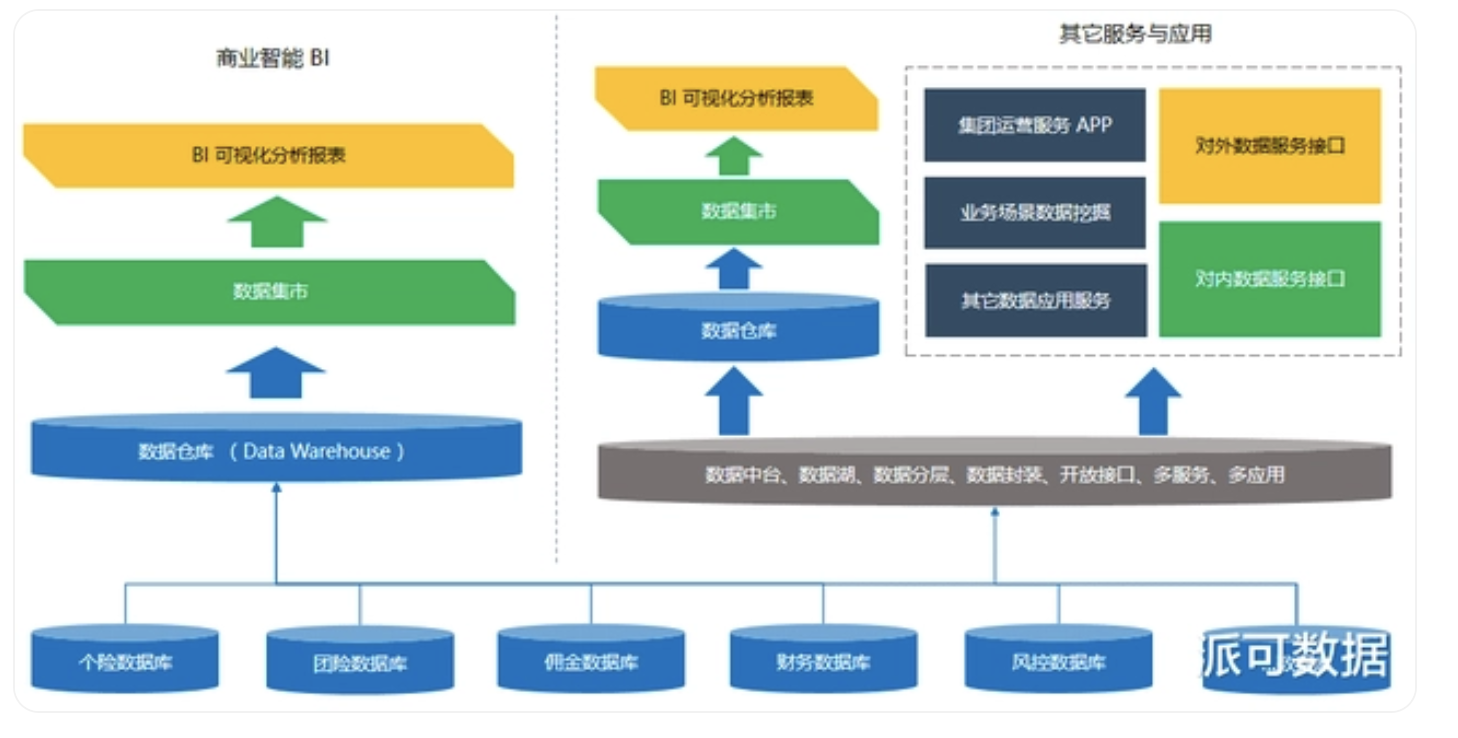
数据库、数据中台、数据仓库、数据湖区别
数据时代,各行业的企业都已经开始通过数据库来沉淀数据,但是真的论起数据库、数据仓库、数据中台,还是新出现的数据湖,它们的概念和区别,可能知道的人就比较少了,今天我们详细来比较了解一下。 一、数据仓…...

缺失的数据范围,思维,hduoj
Problem Description 著名出题人小Q出过非常多的题目,在这个漫长的过程中他发现,确定题目的数据范围是非常痛苦的一件事。 每当思考完一道题目的时间效率,小Q就需要结合时限以及评测机配置来设置合理的数据范围。 因为确定数据范围是一件痛苦…...
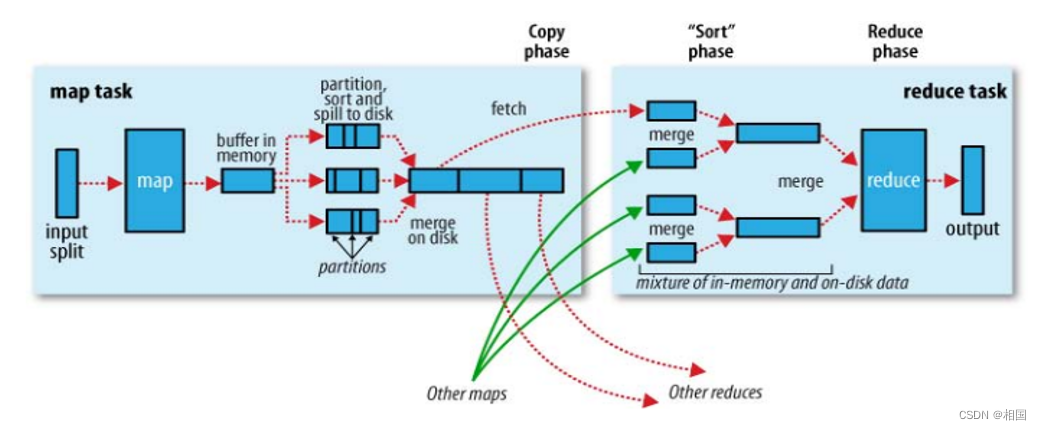
极简的MapReduce实现
目录 1. MapReduce概述 2. 极简MapReduce内存版 3. 复杂MapReduce磁盘版 4. MapReduce思想的总结 1. MapReduce概述 以前写过一篇 MapReduce思想 ,这次再深入一点,简单实现一把单机内存的。MapReduce就是把它理解成高阶函数,需要传入map和…...
)
更新暑假做过的项目(医学数据多标签分类与多标签分割,医学数据二分类)
写在前面 暑假参与了两个项目,收获颇多。搭建网络有许多走过的弯路与经验,调参也是一个必要的技能,在这里想一并分享给大家我在项目中积累的经验和一些小技巧。 PS:结合个人经验与网上经验,大家斟酌自取。 下面的几个…...

谷歌浏览器访问127.0.0.1时报错 Failed to read the ‘sessionStorage‘ property from ‘Window‘
谷歌浏览器访问 127.0.0.1 时报错如下: Uncaught DOMException: Failed to read the ‘sessionStorage’ property from ‘Window’: Access is denied for this document. 原因: 谷歌浏览器设置中禁止了 127.0.0.1 存储数据到浏览器设备上 解决方法…...
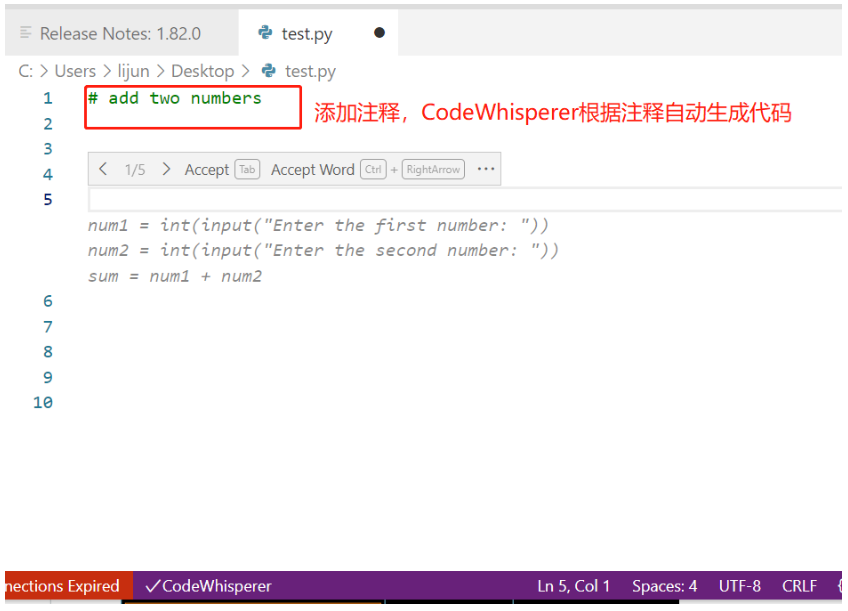
云技术分享 | 快速构建 CodeWhisperer 代码生成服务,让 AI 辅助编程
前言 Amazon CodeWhisperer 是 2023 年 4 月份发布的一款通用的、机器学习驱动的代码生成器服务,CodeWhisperer 经过数十亿行 Amazon 和公开可用代码的训练,可以理解用自然语言(英语)编写的评论,可在集成式开发环境 (…...

开发万岳互联网医院APP:技术要点和关键挑战
随着移动技术和互联网的飞速发展,互联网医院APP成为医疗领域的一项重要创新。这些应用程序为患者和医生提供了更多便利和互动性,但开发互联网医院APP也伴随着一系列的技术要点和关键挑战。本文将探讨互联网医院APP的技术要点以及在开发过程中需要面对的挑…...
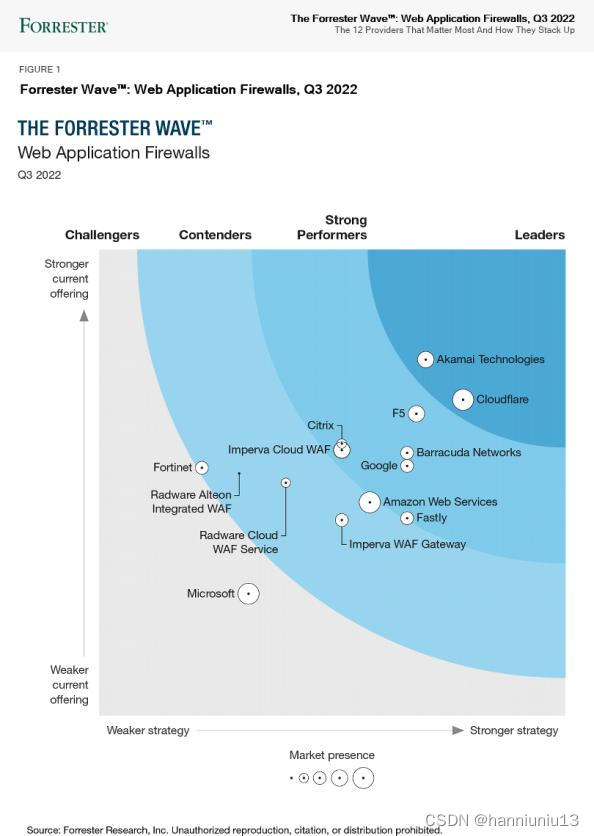
漫谈下一代防火墙与Web应用防火墙的区别
如今,Web应用程序变得越来越复杂,更是黑客非常感兴趣的目标。在谈到网络安全的话题时,我们总会讨论下一代防火墙与Web应用防火墙的区别。当已经拥有下一代防火墙(NGFW)时,为什么需要Web应用程序防火墙&…...

基于马尔可夫随机场的图像去噪算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1、马尔可夫随机场的基本原理 4.2、基于马尔可夫随机场的图像去噪算法 5.算法完整程序工程 1.算法运行效果图预览 原图: 加入噪声的图像: 滤波后的图像 迭代过程…...

【综合类型第 39 篇】HTTP 状态码详解
这是【综合类型第 39 篇】,如果觉得有用的话,欢迎关注专栏。 注: 本篇博客只是在「阿里云开发者社区版 HTTP 状态码详解」中按自己的写作风格做了断句,归纳整理,方便查看和阅读。 尊重原创,原文链接&…...

win10 hosts文件修改不生效
解决办法可以参考:修改hosts 不生效? 三种方法解决...
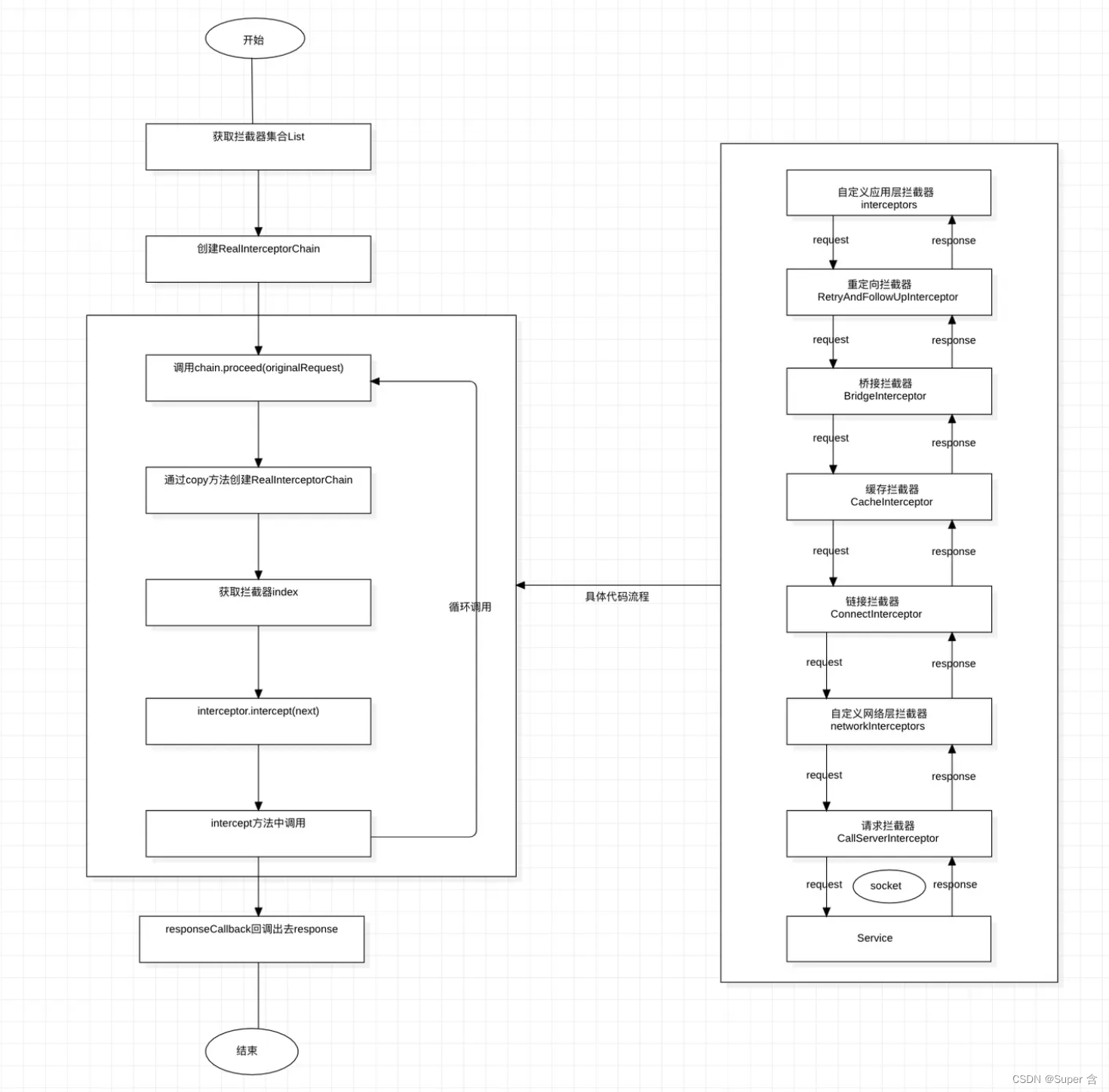
网络库OKHttp(1)流程+拦截器
序、慢慢来才是最快的方法。 背景 OkHttp 是一套处理 HTTP 网络请求的依赖库,由 Square 公司设计研发并开源,目前可以在 Java 和 Kotlin 中使用。对于 Android App 来说,OkHttp 现在几乎已经占据了所有的网络请求操作。 OKHttp源码官网 版…...
关于 Invalid bound statement (not found): 错误的解决
关于 Invalid bound statement not found: 错误的解决 前言错误原因解决方法1. 检查SQL映射文件2. 检查MyBatis配置3. 检查SQL语句4. 检查命名约定5. 清除缓存6. 启用日志记录 重点注意 结语 我是将军我一直都在,。! 前言 当开发Java Spring Boot应用程…...
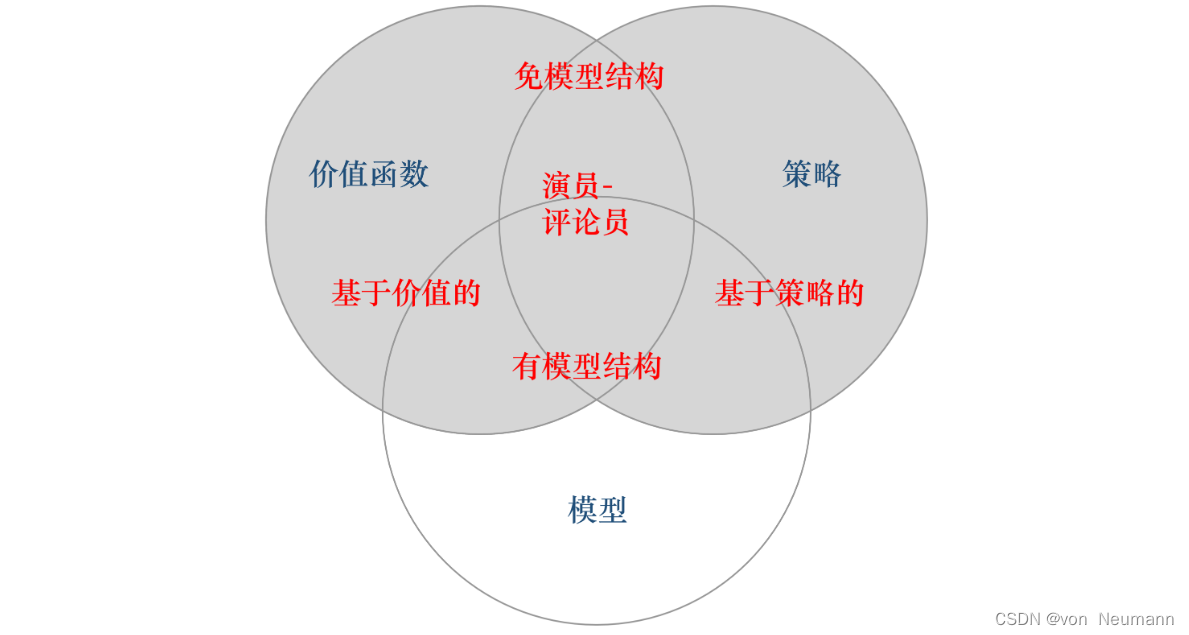
深入理解强化学习——智能体的类型:有模型强化学习智能体与免模型强化学习智能体
分类目录:《深入理解强化学习》总目录 根据智能体学习的事物不同,我们可以把智能体进行归类。基于价值的智能体(Value-based agent)显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。…...
vue项目获得开源代码之后跳过登录界面
readme运行 进入到账号和密码 找到main.js 比如说,以上这段代码 剩下next()就成功进入了...
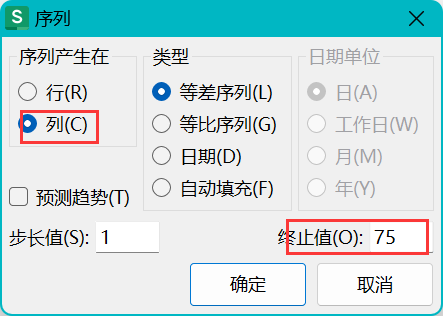
WPS、Excel表格增加一列,序列1到任意大小 / 填充某个范围的数字到列
Excel添加一列递增的数字方法有如下: 一、最常用的,使用鼠标放到右下角下拉增加 1、选中起始框的右下角,直到显示黑色实心十字 2、一直向下拖动 3、成功 这种填充方式是最常用的,100以内都可以轻松瞬间完成 1~100填充 但是如果…...
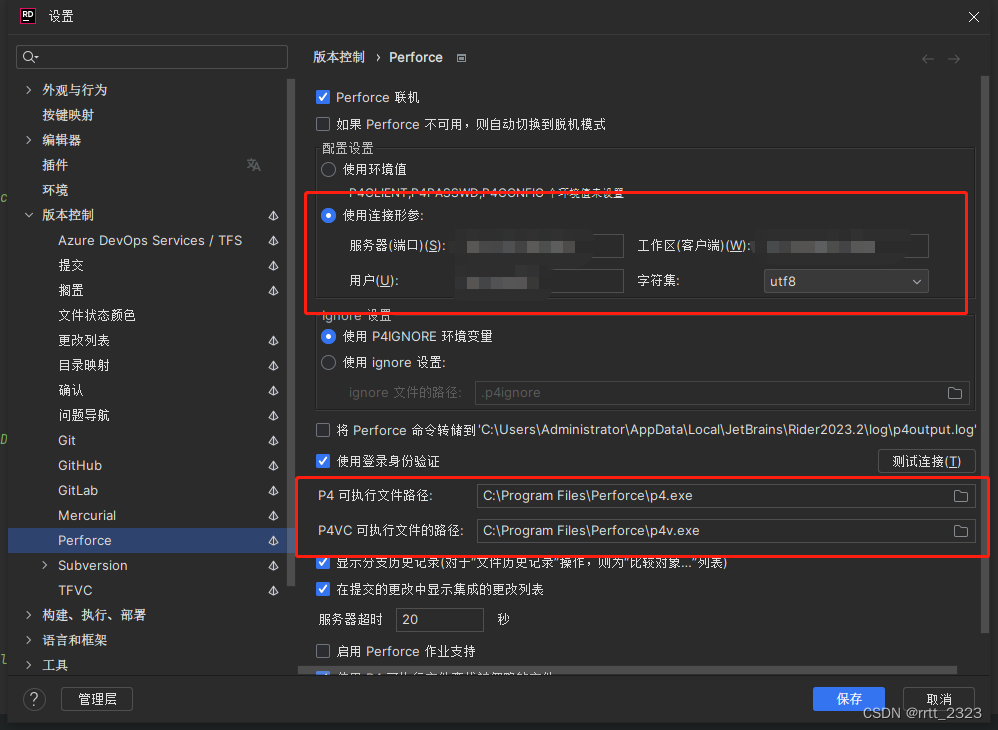
在 rider 里用配置 Perforce(P4)的注意事项
整个配置界面里,关键就配2处位置,但是都有些误导性。 1是连接形参的4个参数都得填,字符集看你项目的要求,这里工作区其实指的是你的工作空间,还不如显示英文的 Workspace 呢,搞得我一开始没填,…...
)
在Spring中,标签管理的Bean中,为什么使用@Autowired自动装配修饰引用类(前提条件该引用类也是标签管理的Bean)
Autowired是Spring框架的一个注解,它可以用来完成自动装配。 自动装配是Spring框架的一个特性,它可以避免手动去注入依赖,而是由框架自动注入。这样可以减少代码的重复性和提高开发效率。 在使用Autowired注解时,Spring会自动搜…...

俄罗斯YandexGPT 2在国家考试中获得高分;OpenAI API开发者快速入门指南
🦉 AI新闻 🚀 俄罗斯YandexGPT 2聊天机器人成功在国家考试中获得高分 摘要:俄罗斯YandexGPT 2聊天机器人通过国家统一考试文学科目,以55分的加权分数成功进入大学。Yandex团队强调他们在开发过程中确保数据库不包含任何关于统考…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
