数据结构--堆
一. 堆
1. 堆的概念
堆(heap):一种有特殊用途的数据结构——用来在一组变化频繁(发生增删查改的频率较高)的数据集中查找最值。
堆在物理层面上,表现为一组连续的数组区间:long[] array ;将整个数组看作是堆。
堆在逻辑结构上,一般被视为是一颗完全二叉树。
满足任意结点的值都大于其子树中结点的值,叫做大堆,或者大根堆,或者最大堆;反之,则是小堆,或者小根堆,或者最小堆。当一个堆为大堆时,它的每一棵子树都是大堆。
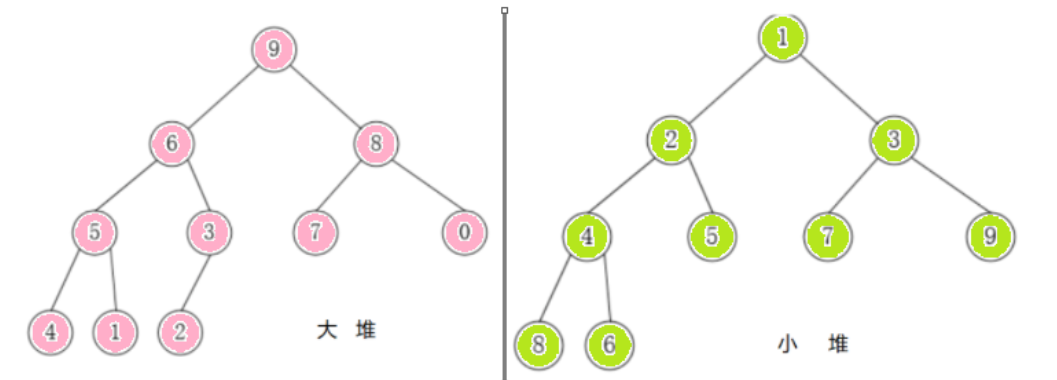
2. 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储;
假设 i 为结点在数组中的下标,则有:
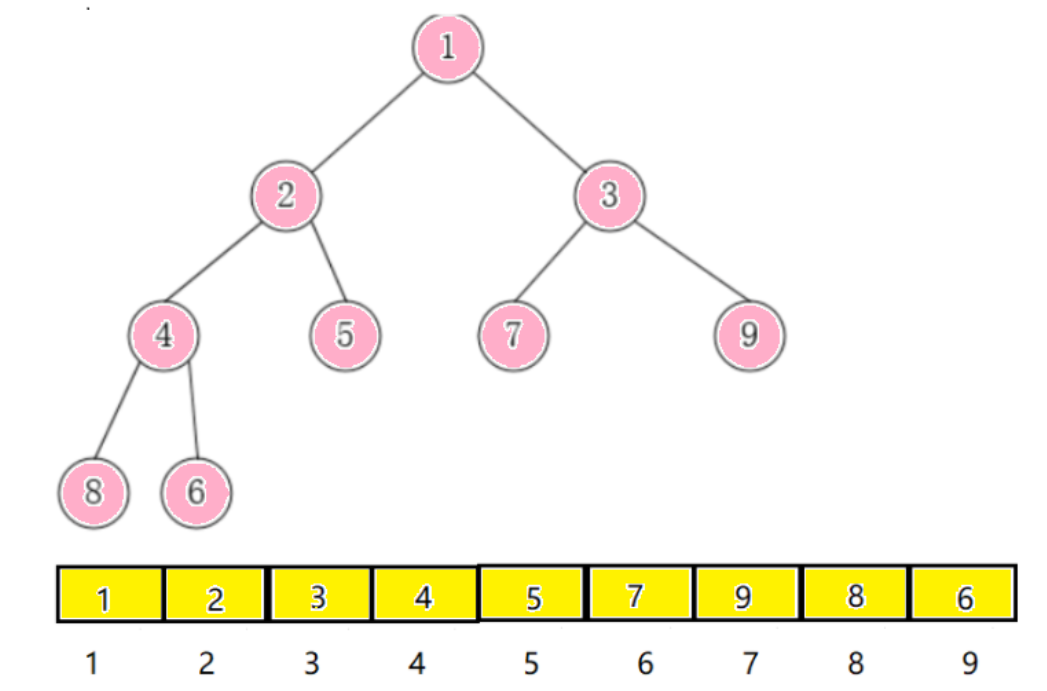
如果 i 为 0,则 i 表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2;
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子;
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子。
二. 堆的基本操作
1. 创建堆,向下调整与向上调整
创建堆只有两种堆可以创建,要不就是大根堆,要不就是小根堆。而要满足大根堆还是小根堆的逻辑,就要向下调整的操作才能实现。要想自己实现堆,堆本身就是一个数组,因此创建一个数组来创建堆。
对于集合 { 27,15,19,18,28,34,65,49,25,37 } 中的数据,如果将其创建成堆呢?
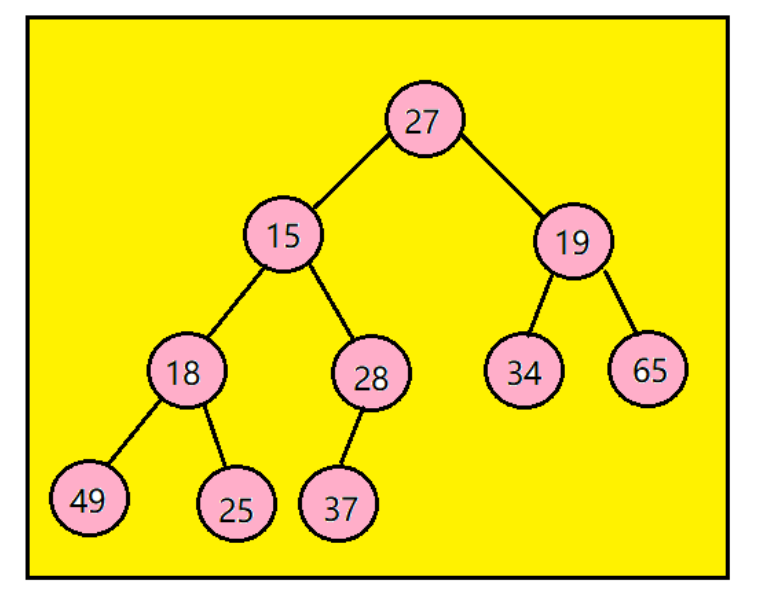
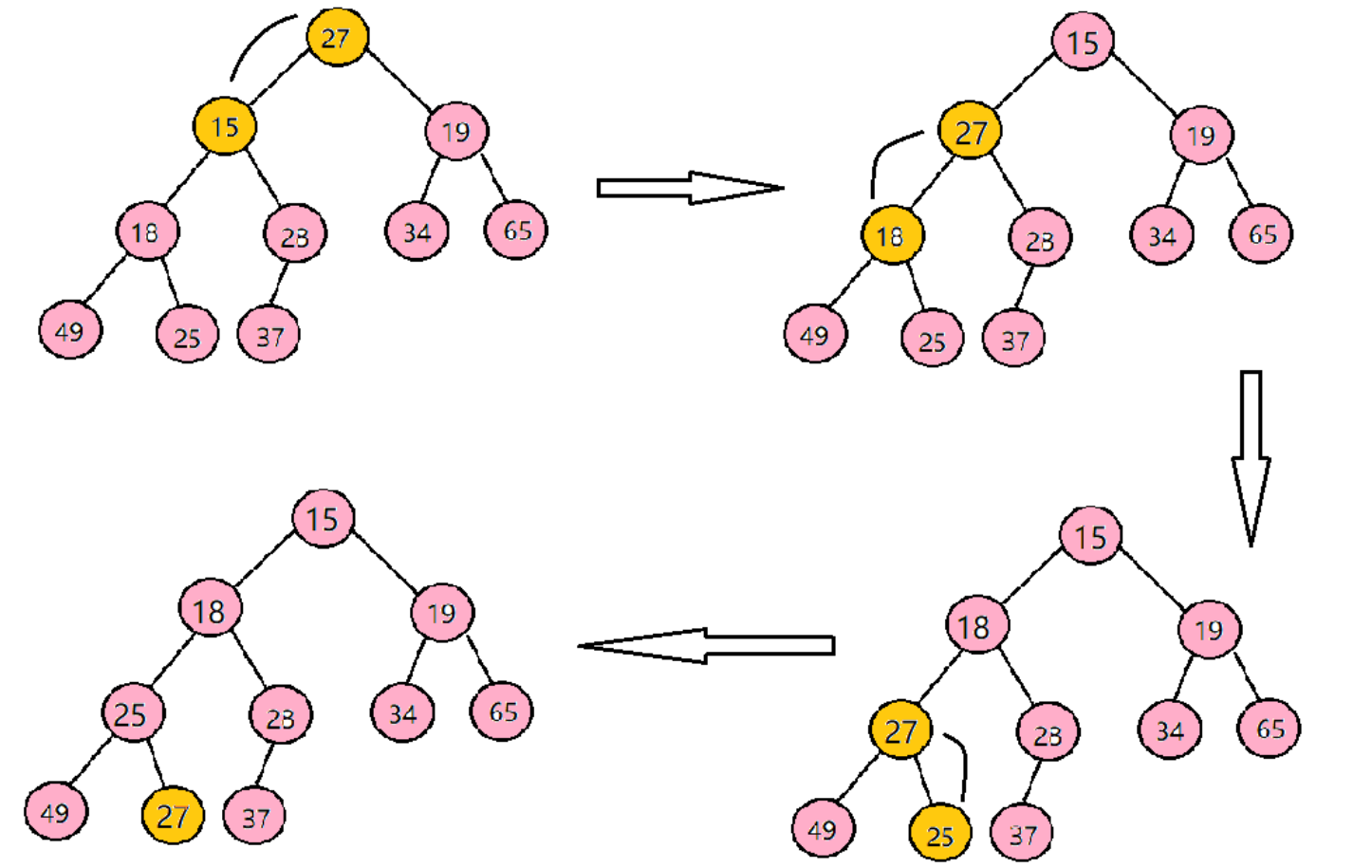
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。 向下过程(以小堆为例):
- 让 parent 标记需要调整的节点,child 标记 parent 的左孩子(注意:parent 如果有孩子一定先是有左 孩子)
- 如果 parent 的左孩子存在,即: child < size, 进行以下操作,直到 parent 的左孩子不存在:
- 看 parent 右孩子是否存在,存在找到左右孩子中最小的孩子,让 child 进行标
- 将 parent 与较小的孩子 child 比较,如果:
- parent 小于较小的孩子 child,调整结束;
- 否则:交换 parent 与较小的孩子 child,交换完成之后,parent 中大的元素向下移动,可能导致子树不满足对的性质,因此需要 继续向下调整,即 parent = child;child = parent*2+1;然后继续 2
def sift(li, low, high):"""建立大根堆:param li: 列表:param low: 堆的根节点位置:param high: 堆的最后一个元素的位置:return:"""i = low # 最开始指向根节点j = 2 * i + 1 # 开始是左孩子tmp = li[low] # 把堆顶存起来# 只要j位置有数while j <= high:# 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子大if j + 1 <= high and li[j + 1] > li[j]:j = j + 1 # 把j指向右孩子# 比较堆顶的tmp和j左右孩子大小比较if li[j] > tmp: # 如果孩子比堆顶大li[i] = li[j] # 把孩子大的换到上面父节点# 往下看一层,将i移动到孩子位置,将j继续向下移动到新i的孩子的位置i = jj = 2 * i + 1else: # tmp更大,把tmp放到i的位置上 结束循环li[i] = tmp # 把tmp放到某一级领导位置上break# 越界了else:li[i] = tmp # 说明i走到最下面一层了,j到还要下一层没有叶子节点位置,是空的,就把tmp放到叶子节点上
def sift(li, low, high):"""建立小根堆:param li: 列表:param low: 堆的根节点位置:param high: 堆的最后一个元素的位置:return:"""i = low # 最开始指向根节点j = 2 * i + 1 # 开始是左孩子tmp = li[low] # 把堆顶存起来# 只要j位置有数while j <= high:# 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子小if j + 1 <= high and li[j + 1] < li[j]:j = j + 1 # 把j指向右孩子# 比较堆顶的tmp和j左右孩子大小比较if li[j] < tmp: # 如果孩子比堆顶小li[i] = li[j] # 把孩子大的换到上面父节点# 往下看一层,将i移动到孩子位置,将j继续向下移动到新i的孩子的位置i = jj = 2 * i + 1else: # tmp更大,把tmp放到i的位置上 结束循环li[i] = tmp # 把tmp放到某一级领导位置上break# 越界了else:li[i] = tmp # 说明i走到最下面一层了,j到还要下一层没有叶子节点位置,是空的,就把tmp放到叶子节点上
建堆的时间复杂度是 O(n) ;向下调整的时间复杂度是 O(log(n))。
2. 堆的插入(offer)
堆的插入总共需要两个步骤:
- 先将元素放入到底层空间中(注意:空间不够时需要扩容)
- 将最后新插入的节点向上调整,直到满足堆的性质 ;
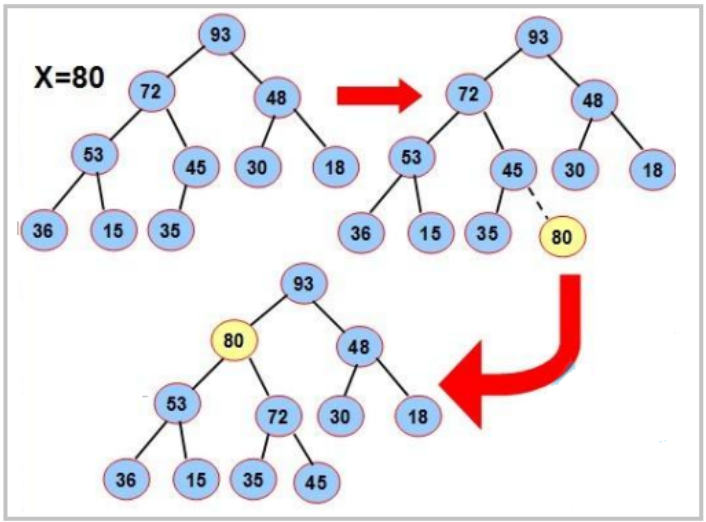
3. 堆的删除(poll)
具体如下:( 注意:堆的删除一定删除的是堆顶元素。)
- 将堆顶元素对堆中最后一个元素交换;
- 将堆中有效数据个数减少一个;
- 对堆顶元素进行向下调整;
代码待补充…
三. 堆的应用
1. 堆排序(从小到大排)
一个数组根据从小到大排序,要创建大堆来排;一个数组根据从大到小排序,要创建小堆来排。
此处就以创建大堆为例。首先将堆顶的元素和堆中的最后一个元素交换,交换后再向下调整,调整后再与堆的倒数第二个元素进行交换。
def sift(li, low, high):"""向下调整的一次过程:param li: 列表:param low: 堆的根节点位置:param high: 堆的最后一个元素的位置:return:"""i = low # 最开始指向根节点j = 2 * i + 1 # 开始是左孩子tmp = li[low] # 把堆顶存起来# 只要j位置有数while j <= high:# 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子大if j + 1 <= high and li[j + 1] > li[j]:j = j + 1 # 把j指向右孩子# 比较堆顶的tmp和j左右孩子大小比较if li[j] > tmp: # 如果孩子比堆顶大li[i] = li[j] # 把孩子大的换到上面父节点# 往下看一层,将i移动到孩子位置,将j继续向下移动到新i的孩子的位置i = jj = 2 * i + 1else: # tmp更大,把tmp放到i的位置上 结束循环li[i] = tmp # 把tmp放到某一级领导位置上break# 越界了else:li[i] = tmp # 说明i走到最下面一层了,j到还要下一层没有叶子节点位置,是空的,就把tmp放到叶子节点上# 堆排序过程
def heap_sort(li):"""1. 先建堆 从最后一个子堆开始,小堆到大堆 依次到根节点2. 向下调整 得到堆顶元素,为最大元素3. 挨个出数 堆顶最大元素和堆最后一个元素交换位置4. 重复2-3,直到堆变空:param li:待排序的列表:return:"""print("开始建大根堆")# n 列表长度n = len(li)# 遍历范围 首先求列表最后一个父元素,最后一个小堆,最后一个子元素下标是n - 1,父下标((n-1)-1))//2,通过左右孩子公式都一样的结果# 最后一个父元素开始,最后-1步长是倒着遍历到列表最后一个元素 找到堆顶0(中间-1,步长负数,-1+1=0),倒序遍历for i in range((n - 2) // 2, -1, -1):sift(li, i, n - 1)# for循环结束,建堆完成了# 挨个出数for i in range(n - 1, -1, -1): # 倒序 i从最后开始# i指向当前堆的最后一个元素li[0], li[i] = li[i], li[0]# 由于是倒序,挨个出数后,尾部有序区指针high,每次左移一位sift(li, 0, i - 1) # i-1是新的highli = [9, 6, 3, 5, 7, 2, 1, 8, 4]print(li)
heap_sort(li)
print(li)
2. top-k问题
若要从N个数字中取得最小的K个数字,则需要创建大小为K的大堆来获取。若要从N个数字中取得最大的K个数字,则需要创建大小为K的小堆来获取。
def sift(li, low, high):"""向上调整的一次过程:param li: 列表:param low: 堆的根节点位置:param high: 堆的最后一个元素的位置:return:"""i = low # 最开始指向根节点j = 2 * i + 1 # 开始是左孩子tmp = li[low] # 把堆顶存起来# 只要j位置有数while j <= high:# 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子小if j + 1 <= high and li[j + 1] < li[j]:j = j + 1 # 把j指向右孩子# 比较堆顶的tmp和j左右孩子大小比较if li[j] < tmp: # 如果孩子比堆顶小li[i] = li[j] # 把孩子大的换到上面父节点# 往下看一层,将i移动到孩子位置,将j继续向下移动到新i的孩子的位置i = jj = 2 * i + 1else: # tmp更大,把tmp放到i的位置上 结束循环li[i] = tmp # 把tmp放到某一级领导位置上break# 越界了else:li[i] = tmp # 说明i走到最下面一层了,j到还要下一层没有叶子节点位置,是空的,就把tmp放到叶子节点上def topk(li, k):# 先取列表前k个元素heap = li[0:k]# 1. 建小根堆for i in range((k - 2) // 2, -1, -1):sift(heap, i, k - 1)print("*" * 80)print("小根堆heap建堆完成,", heap)print("*" * 80)# 2. 遍历 li列表里k后面剩下的元素for i in range(k, len(li)):# 依次拿k后面的值和小根堆 堆顶的值比较大小if li[i] > heap[0]: # 如果值 大于 堆顶元素值heap[0] = li[i] # 把大的值 放到堆顶sift(heap, 0, k - 1)# 3. 挨个出数for i in range(k - 1, -1, -1): # 倒序 i从最后开始# i指向当前堆的最后一个元素heap[0], heap[i] = heap[i], heap[0]sift(heap, 0, i - 1) # i-1是新的highreturn heapli = [i for i in range(20)]
random.shuffle(li)print(li)
print(topk(li, 10))
print(li)
相关文章:

数据结构--堆
一. 堆 1. 堆的概念 堆(heap):一种有特殊用途的数据结构——用来在一组变化频繁(发生增删查改的频率较高)的数据集中查找最值。 堆在物理层面上,表现为一组连续的数组区间:long[] array &…...

Android12之报错 error: BUILD_COPY_HEADERS is obsolete(一百六十七)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

vue前端中v-model与ref的区别
v-model <template><input type"text" v-model"message"> </template>作用:将输入框与message绑定,及将用户输入的内容绑定到message这个变量上,但是message是无法在script中获取到的,要想…...

探索未来:硬件架构之路
文章目录 🌟 硬件架构🍊 基本概念🍊 设计原则🍊 应用场景🍊 结论 📕我是廖志伟,一名Java开发工程师、Java领域优质创作者、CSDN博客专家、51CTO专家博主、阿里云专家博主、清华大学出版社签约作…...

Linux 系统安装 Redis7 —— 超详细操作演示!
内存数据库 Redis7 一、Redis 概述1.1 Redis 简介1.2 Redis 的用途1.3 Redis 特性1.4 Redis 的IO模型 二、Redis 的安装与配置2.1 Redis 的安装2.2 连接前的配置2.3 Redis 客户端分类2.4 Redis 配置文件详解 三、Redis 命令四、Redis 持久化五、Redis 主从集群六、Redis 分布式…...
首次建站用香港服务器有影响没?
对于首次租用香港服务器的朋友来说,难免会对它没有一个很清晰的认知。因此,本文就从香港服务器适用人群,以及建站影响,选择技巧上做一个全方位的解答。 1. 哪一类人群适合使用香港服务器建站? 做外贸业务的网站。香港走的国…...

大数据Flink(九十八):SQL函数的归类和引用方式
文章目录 SQL函数的归类和引用方式 一、SQL 函数的归类...
Python文件共享+cpolar内网穿透:轻松实现公网访问
文章目录 1.前言2.本地文件服务器搭建2.1.Python的安装和设置2.2.cpolar的安装和注册 3.本地文件服务器的发布3.1.Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有广泛的应用&#…...

Flink之源算子Data Source
源算子Data Source 概述内置Data Source基于集合构建基于文件构建基于Socket构建 自定义Data SourceSourceFunctionRichSourceFunction 常见连接器第三方系统连接器File Source连接器DataGen Source连接器Kafka Source连接器RabbitMQ Source连接器MongoDB Source连接器 概述 Fl…...
在雷电模拟器9上安装magisk并安装LSPosed模块以及其Manager管理器(一)
环境:win10 64,雷电模拟器9.0.60(9),Android 9。 之前我都是用雷电模拟器版本4.0.78,Android版本7.1.2,为什么本篇要使用9了呢?先解答下这个问题。原因如下:经过我的测试,LSPosed不支…...
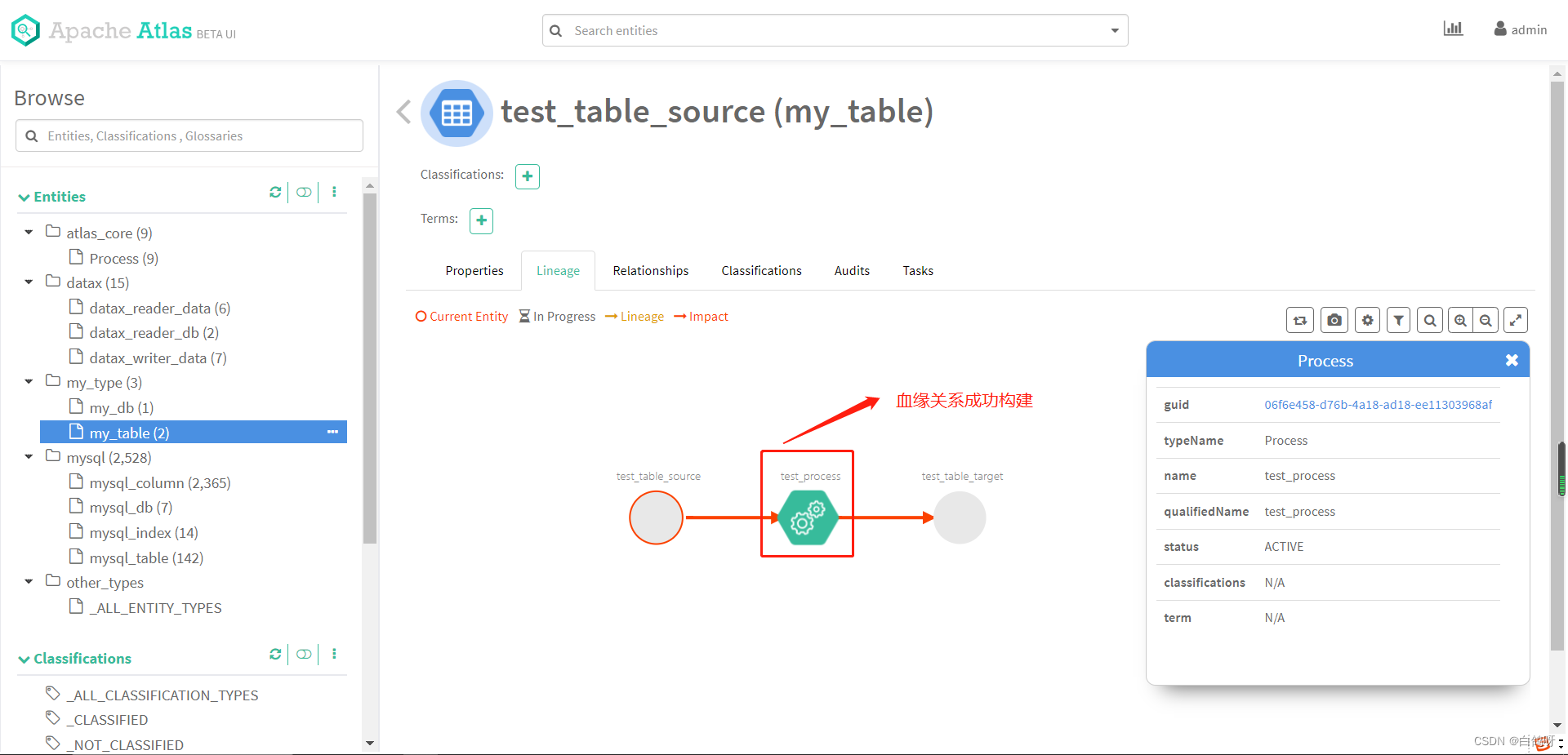
Apache atlas 元数据管理治理平台使用和架构
1、前言 Apache Atlas 是托管于 Apache 旗下的一款元数据管理和治理的产品,目前在大数据领域应用颇为广泛,可以很好的帮助企业管理数据资产,并对这些资产进行分类和治理,为数据分析,数据治理提供高质量的元数据信息。…...

MFF论文笔记
论文名称:Improving Pixel-based MIM by Reducing Wasted Modeling Capability_发表时间:ICCV2023 作者及组织:上海人工智能实验室,西门菲沙大学,香港中文大学 问题与贡献 MIM(Model Maksed Model)方法可以分为两部分…...

Leetcode 02.07 链表相交(链表)
Leetcode 02.07 链表相交(链表) 解法1 尾部对齐解法2:太厉害了,数学归纳推导的方法 很巧妙,这就是将链表的尾端对齐后再一起遍历,这样能满足题目的要求。因为相交之后两个链表到结束的所有节点都一样了&…...

Bootstrap的媒体对象组件(图文展示组件),挺有用的一个组件。
Bootstrap的.media类是用于创建媒体对象的,媒体对象通常用于展示图像(图片)和文本内容的组合,这种布局在展示新闻文章、博客帖子等方面非常常见。.media类使得创建这样的媒体对象非常简单,通常包含一个图像和相关的文本…...
Day2力扣打卡
打卡记录 无限数组的最短子数组(滑动窗口) 链接 思路:先求单个数组的总和,再对两个重复数组所组成的新数组上使用 不定长的滑动窗口 来求得满足目标的最小长度。 class Solution { public:int minSizeSubarray(vector<int>…...
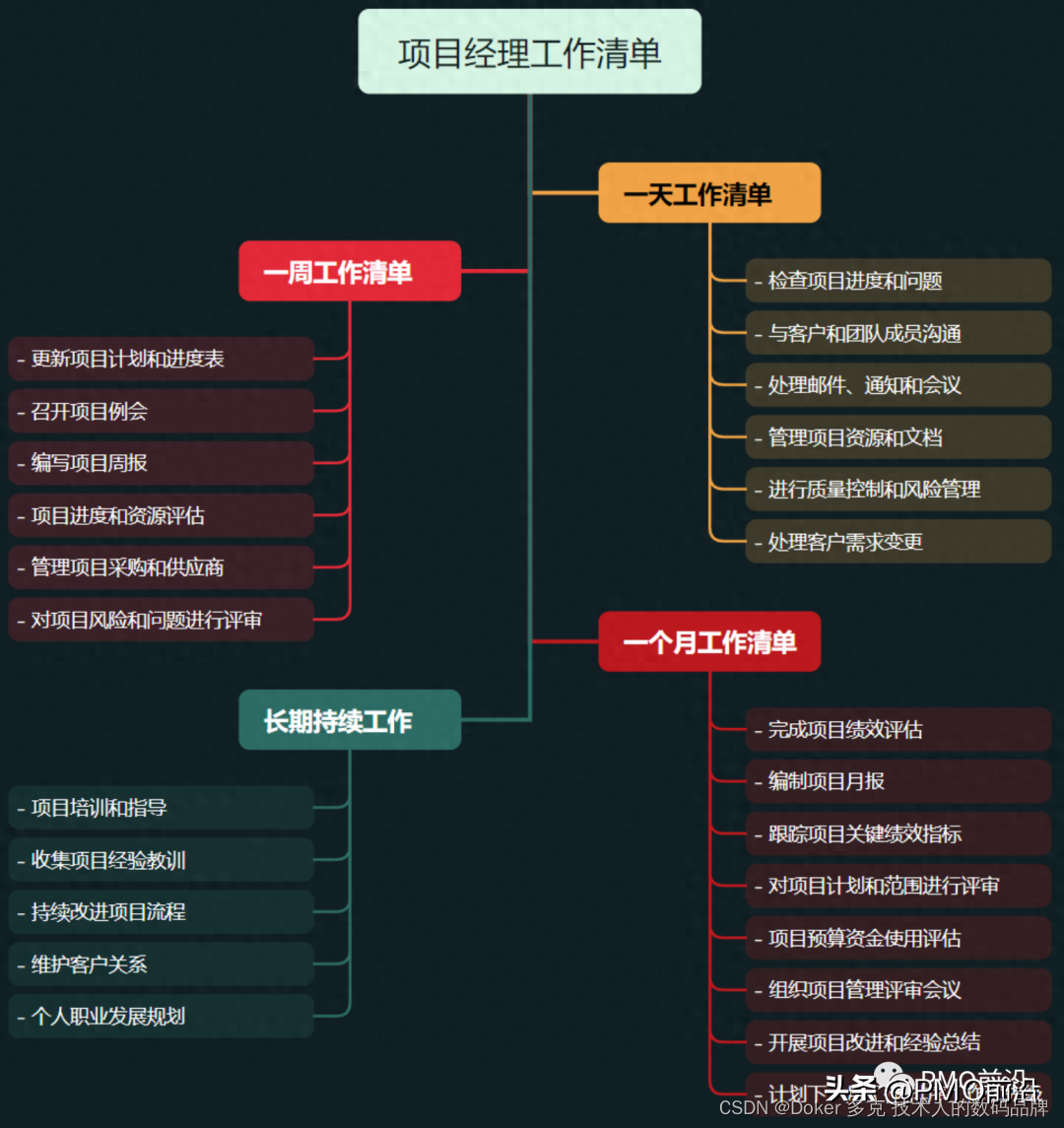
项目经理每天,每周,每月的工作清单
很多不懂项目管理的伙伴问,项目经理每天每周每个月的工作是什么呢? 仿佛他们什么都管,但是又没有具体的产出,但是每天看他们比谁都忙,其实很简单,项目中的每个环节负责具体的事情,但是每个环节…...
Java —— 运算符
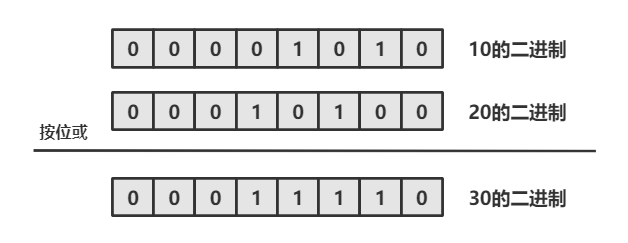
目录 1. 什么是运算符 2. 算术运算符 2.1 基本四则运算符: 加减乘除模( - * / %) 2.2 增量运算符 - * %与 自增/自减运算符 -- 3. 关系运算符 4. 逻辑运算符 4.1 逻辑与 && 4.2 逻辑或|| 4.3 逻辑非 ! 4.4 短路求值 5. 位运算符 5.1 按位与 & 5.2 按位或 5.3 按位…...

【C++ 中的友元函数:解密其神秘面纱】
友元函数,作为C中一个重要但常常被误解的概念,经常让初学者感到困惑。本文将带您逐步了解友元函数的含义、用途以及如何正确使用它们。 什么是友元函数? 在C中,友元函数是一种特殊的函数,它允许某个类或类的成员函数…...
YOLOv8涨点技巧:手把手教程,注意力机制如何在不同数据集上实现涨点的工作,内涵多种网络改进方法
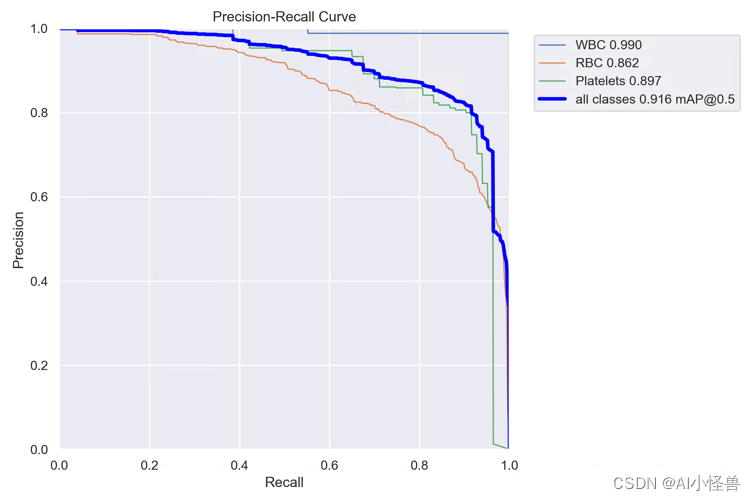
💡💡💡本文独家改进:手把手教程,解决注意力机制引入到YOLOv8在自己数据集不涨点的问题点,本文提供五种改进方法来解决此问题; ContextAggregation | 亲测在血细胞检测项目中涨点,…...

牛客:FZ12 牛牛的顺时针遍历
FZ12 牛牛的顺时针遍历 文章目录 FZ12 牛牛的顺时针遍历题目描述题解思路题解代码 题目描述 题解思路 通过一个变量来记录当前方向,遍历矩阵,每次遍历一条边,将该边的信息加入到结果中 题解代码 func spiralOrder(matrix [][]int) []int {…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
