代码随想录【Day25】| 216. 组合总和 III、17. 电话号码的字母组合
216. 组合总和 III
题目链接
题目描述:
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]
示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]
难点:
思路:
- 递归进入下一层时,传入剩余需要的总和数
- 总和数为0(减去已被添加元素值)和元素个数为k均满足,添加至结果集
- 剪枝:当前所需总和小于零 或 结果集元素个数大于k 直接返回
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();int curSum;public List<List<Integer>> combinationSum3(int k, int n) {backtracking(n, k, 1);return result;}public void backtracking(int n, int k, int startIdx) {if (n < 0 || path.size() > k) return; // 当前所需总和小于零 或 结果集元素个数大于kif (path.size() == k && n == 0) { // 总和数和元素个数均满足result.add(new ArrayList<>(path));return;}for (int i = startIdx; i <= 9; i++) {path.add(i);curSum += i;backtracking(n-i, k, i+1); // 传入剩余需要的总和数path.remove(path.size()-1);curSum -= i;}}
}
时长:
15min
收获:
17. 电话号码的字母组合
题目链接
题目描述:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例:
- 输入:“23”
- 输出:[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
难点:
多层for循环不可取。。。。
这题有难度的。。。
思路:
class Solution {List<String> result = new ArrayList<>();//每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuilderStringBuilder path = new StringBuilder();public List<String> letterCombinations(String digits) {if (digits == null || digits.length() == 0) return result;//因为数据规模不大,采用数组结构存储映射关系。//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""String[] numStrs = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};backtracking(digits, numStrs, 0);return result;}public void backtracking(String digits, String[] numStrs, int num) {//num代表递归层数,也代表拼接的字符数量if (num == digits.length()) {result.add(path.toString());return;}//str 表示当前num对应的字符串String str = numStrs[digits.charAt(num)-'0'];for (int i = 0; i < str.length(); i++) {path.append(str.charAt(i));backtracking(digits, numStrs, num+1);path.deleteCharAt(path.length()-1);}}
}
时长:
30min
收获:
递归参数传递不要用num++这种啊啊啊啊,num是自增的!不对不对!!!
相关文章:

代码随想录【Day25】| 216. 组合总和 III、17. 电话号码的字母组合
216. 组合总和 III 题目链接 题目描述: 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。 说明: 所有数字都是正整数。 解集不能包含重复的组合。 示例 1: 输入: k 3, n 7 输…...
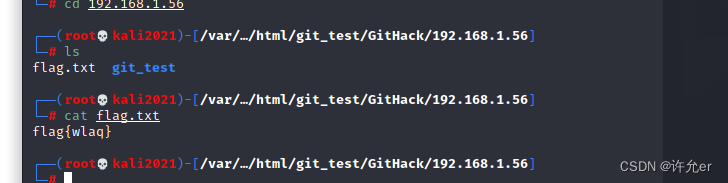
web中git漏洞的形成的原理及使用
目录 1.Git漏洞的成因 1.不正确的权限设置: 2.代码注入漏洞: 3.未经身份验证的访问: 4.非安全传输: 5.跨站脚本攻击(XSS): 2.git泄露环境的搭建 git init: git add࿱…...
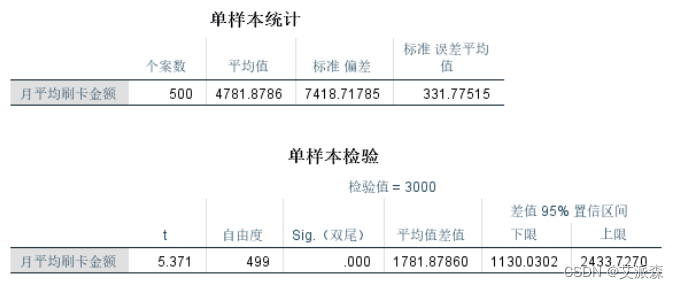
【SPSS】单样本T检验分析详细操作教程(附案例实战)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
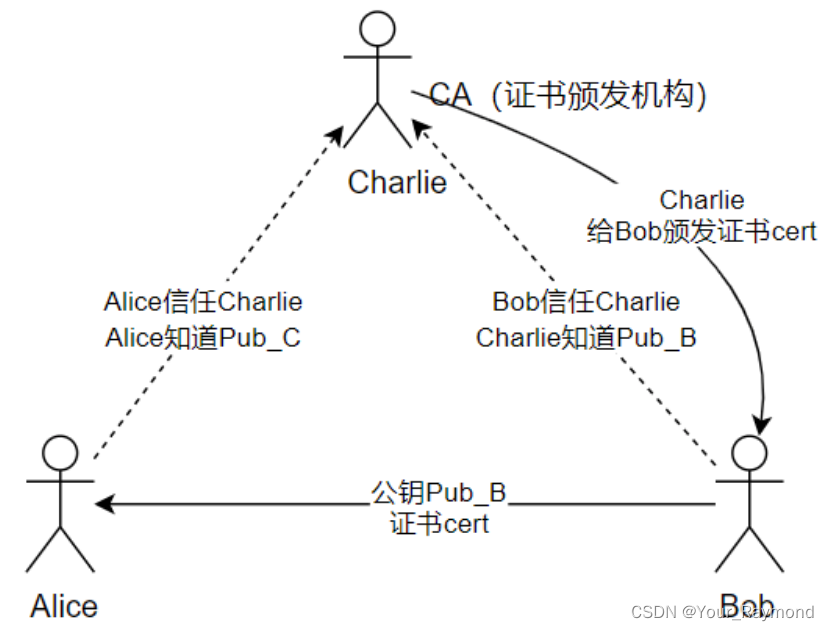
计算机网络笔记、面试八股(三)—— HTTPS协议
本章目录3. HTTPS协议3.1 HTTPS协议简介3.2 SSL/TLS协议3.2.1 SSL/TLS功能的实现3.3 HTTP和HTTPS的区别3.4 HTTPS协议的优点3.5 HTTPS协议的缺点3.6 HTTPS协议的工作流程3.7 HTTPS是如何解决HTTP的缺点的3.7.1 解决内容可能被窃听的问题——加密3.7.1.1 方法1.对称加密3.7.1.2 …...
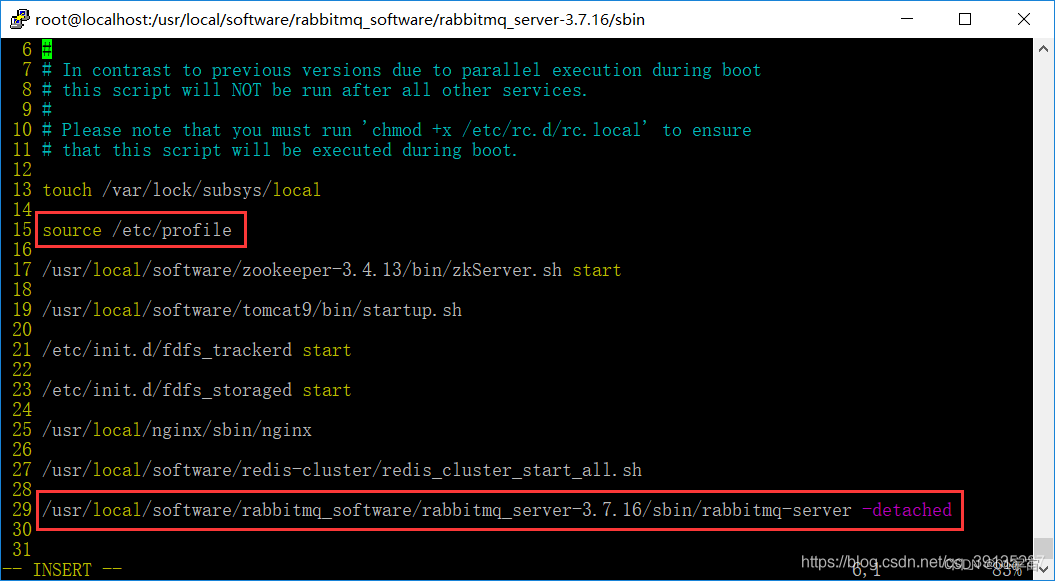
浅谈liunx init.d 和 rc.local 两种起动方式
浅谈liunx init.d 和 rc.local 两种起动方式 以rabbitmq 举例 (一).init.d 方式 开机自动重启设置 1.在/etc/init.d 目录下新建一个 rabbitmq [rootlocalhost init.d]# vi rabbitmq具体脚本如下所示: #!/bin/bash # # chkconfig: 2345 …...

元宇宙+教育,正在引发哪些剧烈变革?机会在哪里?丨圆桌实录
图片来源:由无界AI绘画工具生成2月23日,温州元宇宙创新中心为2023年第一批申请入驻的项目企业举办了签约仪式。温州临境网络科技有限公司、温州好玩文化产业有限公司、温州云兮科技有限公司(筹)等企业完成签约。这意味着ÿ…...
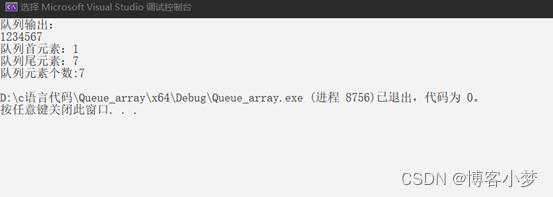
追梦之旅【数据结构篇】——详解C语言实现顺序队列
详解C语言实现顺序队列~😎前言🙌预备小知识🙌队列的概念及结构😊1.顺序队列头文件编写🙌2.Queue.c文件的编写🙌1)队列的初始化函数实现😊2)队列的销毁函数实现Ƕ…...

使用自己的数据集Fine-tune PaddleHub预训练模型
使用自己的数据Fine-tune PaddleHub预训练模型 果农需要根据水果的不同大小和质量进行产品的定价,所以每年收获的季节有大量的人工对水果分类的需求。基于人工智能模型的方案,收获的大堆水果会被机械放到传送带上,模型会根据摄像头拍到的图片…...

带组态物联网平台源码 代码开源可二次开发 web MQTT Modbus
物联网IOT平台开发辅助文档 技术栈:JAVA [ springmvc / spring / mybatis ] 、Mysql 、Html 、 Jquery 、css 使用协议和优势: TCP/IP、HTTP、MQTT 通讯协议 1.1系统简介 IOT通用物联网系统平台带组态,是一套面向通用型业务数据处理的系统…...

计算机网络的发展历程
计算机网络的历史可以追溯到20世纪60年代。那个时候,计算机还非常昂贵,只有少数大型机可以被用于处理重要任务。这些大型机通常被安装在大型企业、政府机构和大学中。由于这些机器非常昂贵,许多企业、机构和大学只能通过终端连接来访问它们。…...

【华为OD机试模拟题】用 C++ 实现 - 不含 101 的数(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

面试题-下单后位置信息上报的方案
面试题:外卖下单后每10min上报位置事件的具体实现方案。需要考虑哪些点。存储方案:考虑到数据量很大,需要快速响应查询请求,建议使用分布式存储方案,如 HBase、MongoDB 等。这些分布式存储系统可以水平扩展,…...
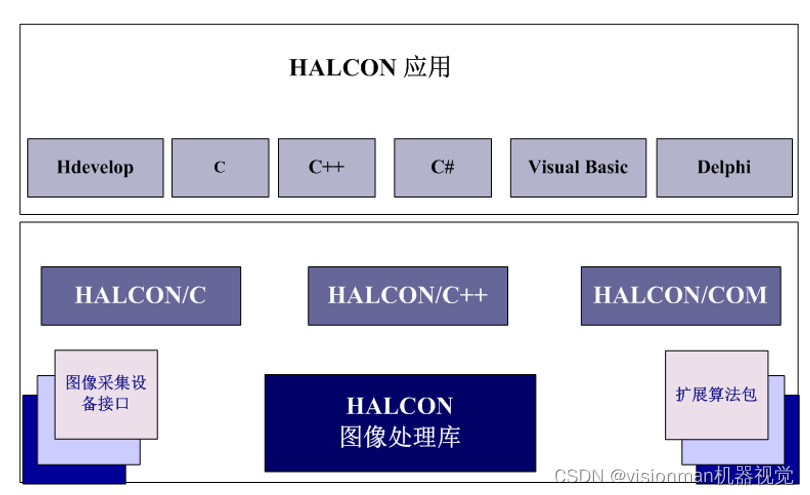
视觉人培训团队把它称之为,工业领域人类最伟大的软件创造,它的名字叫Halcon
目前为止,世界上综合能力强大的机器视觉软件,,它的名字叫Halcon。 视觉人培训团队把它称之为,工业领域人类最伟大的软件创造,它的名字叫Halcon。 持续不断更新最新的图像技术,软件综合能力持续提升。 综…...
干了2年的手工点点点,感觉每天浑浑噩噩,我的自动化测试之路...
作为一个测试人员,从业年期从事手工测试的工作是没有太多坏处的,当然,如果一直点来点去那么确实自身得不到提高,这时候选择学习自动化测试是一件很有必要的事情,一来将自己从繁重的重复工作中解放出来,从事…...
嵌入式系统硬件设计与实践(学习方法)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 刚读书的时候,对什么是嵌入式,其实并不太清楚。等到自己知道的时候,已经毕业很多年了。另外对于计算机毕业的学…...
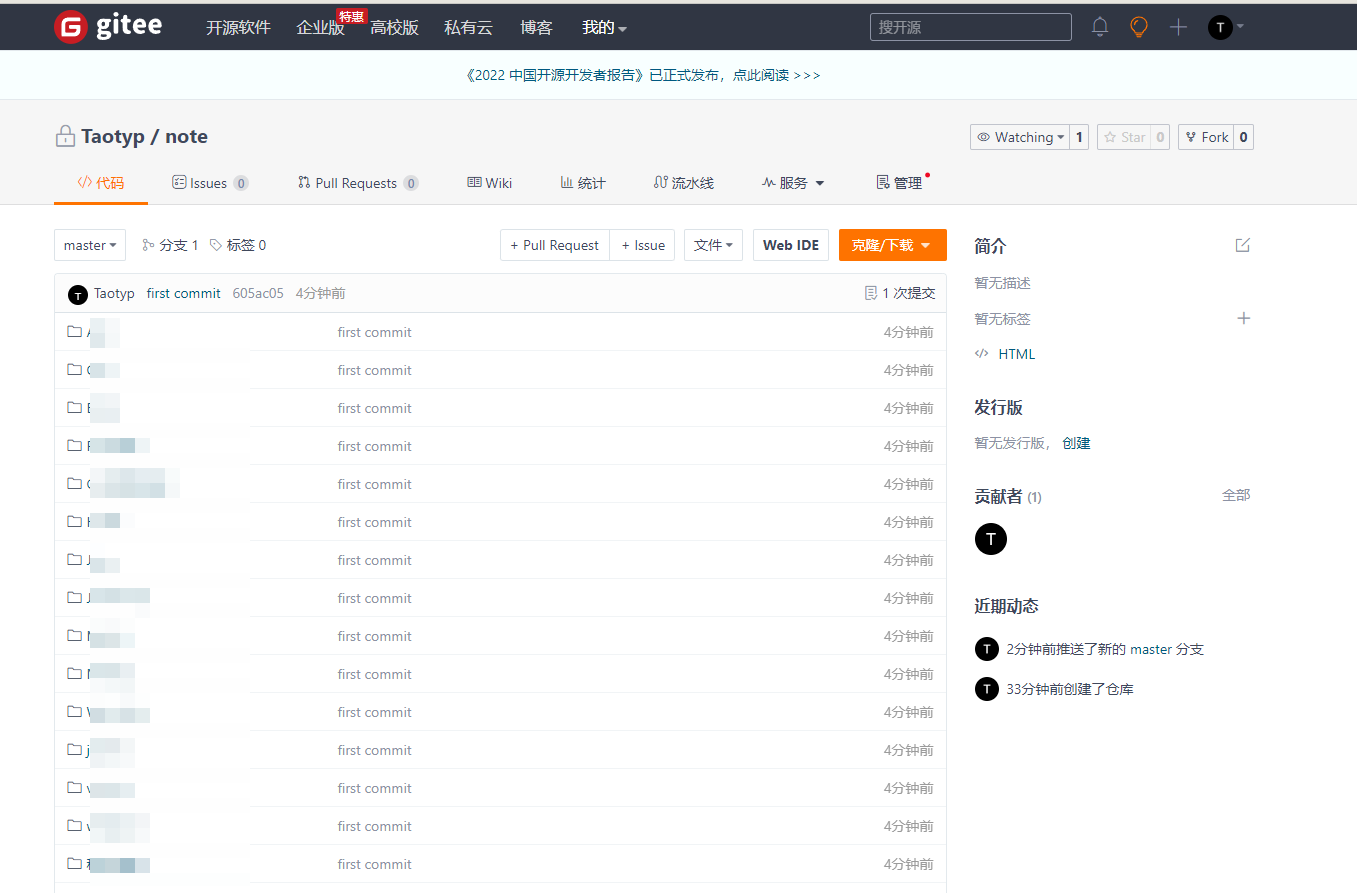
如何拥有自己的Gitee代码仓库
本教程适用码云代码托管平台 https://gitee.com/ 首先在电脑上安装Git(哔站有安装Git教程)和注册gitee账号后再来阅读此教程 1、在设置页面中点击 SSH公钥 2、点击 怎样生成公钥 3、点击公钥管理 4、点击 生成\添加SSH公钥 5、打开终端 输入如图红框中的…...
通用信息抽取技术UIE产业案例解析,Prompt 范式落地经验分享!
想了解用户的评价究竟是“真心夸赞”还是“阴阳怪气”?想快速从多角色多事件的繁杂信息中剥茧抽丝提取核心内容?想通过聚合相似事件准确地归纳出特征标签?……想了解UIE技术在产业中的实战落地经验?通用信息抽取技术 UIE 产业案例…...
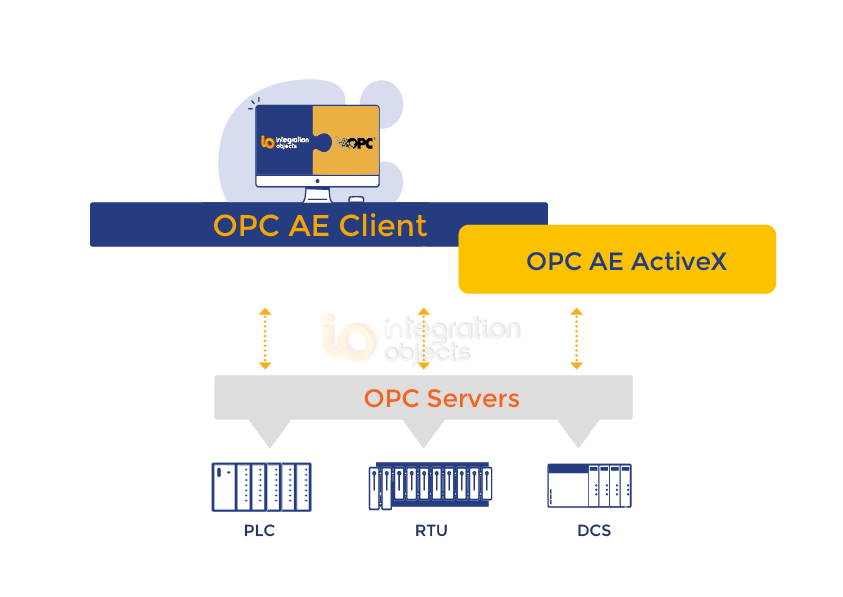
integrationobjects/OPC AE Client ActiveX Crack
使用 OPC AE 客户端 ActiveX 进行快速 OPC 警报和事件客户端编程! OPC AE Client ActiveX包括多个 OPC ActiveX 控件,可以轻松嵌入到最流行的 OLE 容器中。这允许用户与任何 OPC AE 服务器连接并实时检索警报和事件。 这种易于使用的 OPC AE ActiveX 简化…...
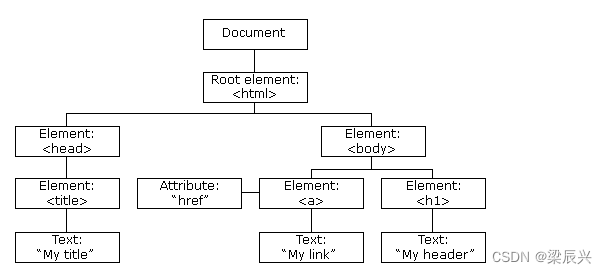
JavaScript HTML DOM 简介
文章目录JavaScript HTML DOM 简介HTML DOM (文档对象模型)HTML DOM 树查找 HTML 元素通过 id 查找 HTML 元素通过标签名查找 HTML 元素通过类名找到 HTML 元素下面我们将学到如下内容JavaScript HTML DOM 简介 通过 HTML DOM,可访问 JavaScript HTML 文档的所有元素…...
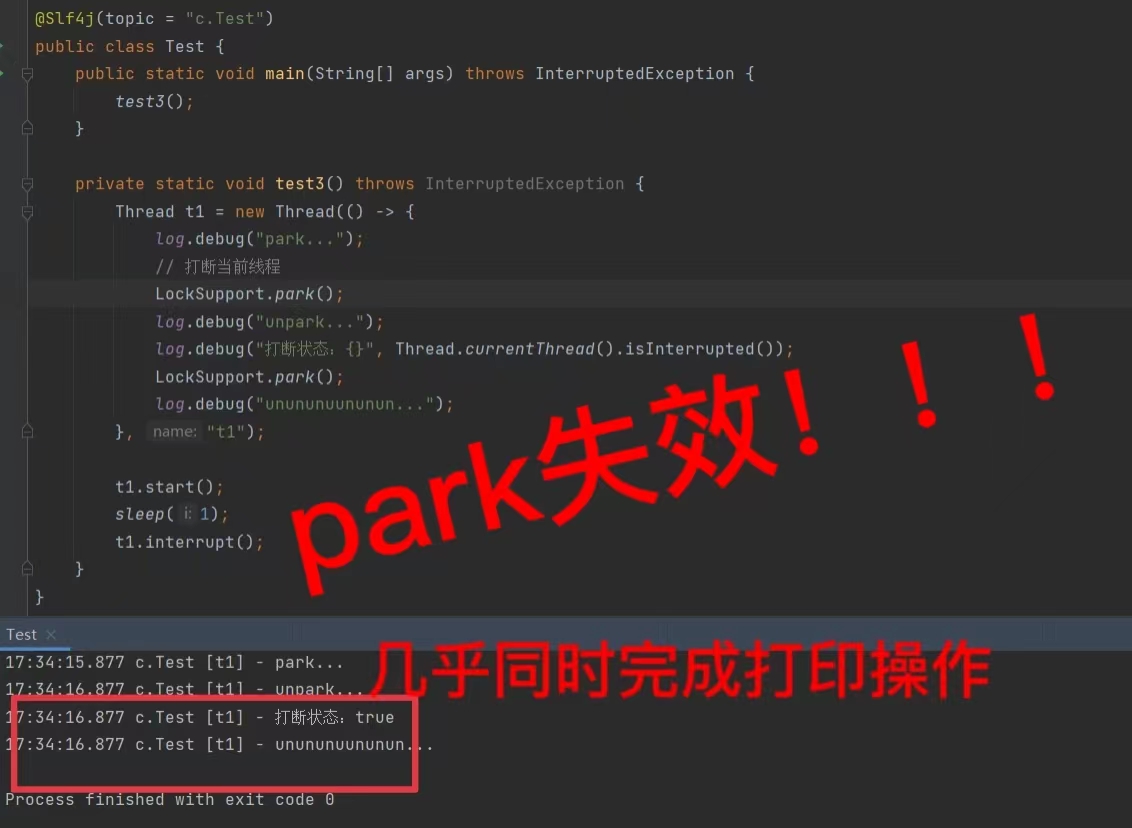
interrupt多线程设计模式
1. 两阶段终止-interrupt Two Phase Termination 在一个线程T1中如何“优雅”终止线程T2?这里的【优雅】指的是给T2一个料理后事的机会。 错误思路 ● 使用线程对象的stop()方法停止线程(强制杀死) —— stop()方法…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
