深度学习——卷积神经网络(CNN)基础二
深度学习——卷积神经网络(CNN)基础二
文章目录
- 前言
- 三、填充和步幅
- 3.1. 填充
- 3.2. 步幅
- 3.3. 小结
- 四、多输入多输出通道
- 4.1. 多输入通道
- 4.2. 多输出通道
- 4.3. 1×1卷积层
- 4.4. 小结
- 总结
前言
上文对卷积有了初步的认识,其实卷积操作就是通过卷积核对每个通道的矩阵从左到右、从上至下进行互相关运算(可以提取图像中的特征,卷积窗口的填充和滑动步长都是超参数)得到一个输出矩阵,最后把多个通道的值也对应加起来得到最终的输出值。本章将继续学习有关知识。
三、填充和步幅
按前面所学内容,假设输入形状为 n h × n w n_h\times n_w nh×nw,卷积核形状为 k h × k w k_h\times k_w kh×kw,那么输出形状将是 ( n h − k h + 1 ) × ( n w − k w + 1 ) (n_h-k_h+1) \times (n_w-k_w+1) (nh−kh+1)×(nw−kw+1)。
因此,卷积的输出形状取决于输入形状和卷积核的形状。
填充(padding)和*步幅(stride)*这两个因素会影响输出的大小
假设以下情景:
有时,在应用了连续的卷积之后,我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于 1 1 1所导致的。比如,一个 240 × 240 240 \times 240 240×240像素的图像,经过 10 10 10层 5 × 5 5 \times 5 5×5的卷积后,将减少到 200 × 200 200 \times 200 200×200像素。如此一来,原始图像的边界丢失了许多有用信息。而填充是解决此问题最有效的方法;
有时,我们可能希望大幅降低图像的宽度和高度。例如,如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。
3.1. 填充
如上所述,在应用多层卷积时,我们常常丢失边缘像素。解决这个问题的简单方法即为填充:在输入图像的边界填充元素(通常填充元素是 0 0 0)。
我们将 3 × 3 3 \times 3 3×3输入填充到 5 × 5 5 \times 5 5×5,那么它的输出就增加为 4 × 4 4 \times 4 4×4。阴影部分是第一个输出元素以及用于输出计算的输入和核张量元素:

通常,如果我们添加 p h p_h ph行填充(大约一半在顶部,一半在底部)和 p w p_w pw列填充(左侧大约一半,右侧一半),则输出形状将为
( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) 。 (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1)。 (nh−kh+ph+1)×(nw−kw+pw+1)。
这意味着输出的高度和宽度将分别增加 p h p_h ph和 p w p_w pw。
在许多情况下,我们需要设置 p h = k h − 1 p_h=k_h-1 ph=kh−1和 p w = k w − 1 p_w=k_w-1 pw=kw−1,使输入和输出具有相同的高度和宽度。
这样可以在构建网络时更容易地预测每个图层的输出形状。
卷积神经网络中卷积核的高度和宽度通常为奇数,例如1、3、5或7。
选择奇数的好处是,保持空间维度的同时,我们可以在顶部和底部填充相同数量的行,在左侧和右侧填充相同数量的列。
此外,使用奇数的核大小和填充大小也提供了书写上的便利。对于任何二维张量X,当满足:
- 卷积核的大小是奇数;
- 所有边的填充行数和列数相同;
- 输出与输入具有相同高度和宽度
则可以得出:输出Y[i, j]是通过以输入X[i, j]为中心,与卷积核进行互相关计算得到的。
比如,在下面的例子中,我们创建一个高度和宽度为3的二维卷积层,并(在所有侧边填充1个像素)。给定高度和宽度为8的输入,则输出的高度和宽度也是8。
#定义一个计算卷积的函数(初始化卷积层权重,并对输入和输出扩大和缩减相应的维数)
def comp_conv2d(conv2d,x):x = x.reshape((1,1)+x.shape)# 这里的(1,1)表示批量样本大小和通道数都为1y = conv2d(x)return y.reshape(y.shape[2:]) #省去前两个维度#这里每侧边都填充了1行1列,因此共填充了2行2列
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1)
x = torch.rand(size=(8,8))
print(comp_conv2d(conv2d,x).shape)#当卷积核的高度和宽度不同时,我们可以填充不同的高度和宽度
conv2d = nn.Conv2d(1,1,kernel_size=(5,3),padding=(2,1))
print(comp_conv2d(conv2d,x).shape)#结果:
torch.Size([8, 8])
torch.Size([8, 8])
3.2. 步幅
在计算互相关时,卷积窗口从输入张量的左上角开始,向下、向右滑动。 之前我们默认每次滑动一个元素。 但是,有时候为了高效计算或是缩减采样次数,卷积窗口可以跳过中间位置,每次滑动多个元素, 而每次滑动元素的数量称为步幅(stride)
如图是垂直步幅为 3 3 3,水平步幅为 2 2 2的二维互相关运算:

通常,当垂直步幅为 s h s_h sh、水平步幅为 s w s_w sw时,输出形状为:
⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ . \lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor. ⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋.
如果我们设置了 p h = k h − 1 p_h=k_h-1 ph=kh−1和 p w = k w − 1 p_w=k_w-1 pw=kw−1,则输出形状将简化为 ⌊ ( n h + s h − 1 ) / s h ⌋ × ⌊ ( n w + s w − 1 ) / s w ⌋ \lfloor(n_h+s_h-1)/s_h\rfloor \times \lfloor(n_w+s_w-1)/s_w\rfloor ⌊(nh+sh−1)/sh⌋×⌊(nw+sw−1)/sw⌋。
更进一步,如果输入的高度和宽度可以被垂直和水平步幅整除,则输出形状将为 ( n h / s h ) × ( n w / s w ) (n_h/s_h) \times (n_w/s_w) (nh/sh)×(nw/sw)。
下面,我们将高度和宽度的步幅设置为2,从而将输入的高度和宽度减半。
#步幅
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2)
print(comp_conv2d(conv2d,x).shape)
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
print(comp_conv2d(conv2d, x).shape)#结果:
torch.Size([4, 4])
torch.Size([2, 2])默认情况下,填充为0,步幅为1。在实践中,我们很少使用不一致的步幅或填充,也就是说,我们通常有ph=pw和sh=sw。
3.3. 小结
- 填充可以增加输出的高度和宽度。这常用来使输出与输入具有相同的高和宽。
- 步幅可以减小输出的高和宽,
- 填充和步幅可用于有效地调整数据的维度。
四、多输入多输出通道
当我们添加通道时,我们的输入和隐藏的表示都变成了三维张量。例如,每个RGB输入图像具有3×h×w的形状。我们将这个大小为3的轴称为通道(channel)维度。
4.1. 多输入通道
当输入包含多个通道时,需要构造一个与输入数据具有相同输入通道数的卷积核,以便与输入数据进行互相关运算
假设输入的通道数为 c i c_i ci,那么卷积核的输入通道数也需要为 c i c_i ci。如果卷积核的窗口形状是 k h × k w k_h\times k_w kh×kw,那么当 c i = 1 c_i=1 ci=1时,我们可以把卷积核看作形状为 k h × k w k_h\times k_w kh×kw的二维张量。
当 c i > 1 c_i>1 ci>1时,我们卷积核的每个输入通道将包含形状为 k h × k w k_h\times k_w kh×kw的张量。将这些张量 c i c_i ci连结在一起可以得到形状为 c i × k h × k w c_i\times k_h\times k_w ci×kh×kw的卷积核。由于输入和卷积核都有 c i c_i ci个通道,我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算,再对通道求和(将 c i c_i ci的结果相加)得到二维张量。

对图中所示用代码实现一下:
def corr2d_multi_in(x,k):return sum(d2l.corr2d(x,k) for x,k in zip(x,k))
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])print(corr2d_multi_in(X, K))#结果:
tensor([[ 56., 72.],[104., 120.]])4.2. 多输出通道
每一层有多个输出通道是至关重要的。在最流行的神经网络架构中,随着神经网络层数的加深,我们常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度。
我们可以将每个通道看作对不同特征的响应。而现实可能更为复杂一些,因为每个通道不是独立学习的,而是为了共同使用而优化的。因此,多输出通道并不仅是学习多个单通道的检测器。
def corr2d_multi_in_out(X, K):# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。# 最后将所有结果都叠加在一起return torch.stack([corr2d_multi_in(X, k) for k in K], 0)K = torch.stack((K, K + 1, K + 2), 0)
print(K.shape) #卷积核的数量是由K的第一个维度决定的,故这里是有三个卷积核(卷积核的输出通道数与卷积核的数量对应)
print(corr2d_multi_in_out(X,K))#结果:
torch.Size([3, 2, 2, 2])
tensor([[[ 56., 72.],[104., 120.]],[[ 76., 100.],[148., 172.]],[[ 96., 128.],[192., 224.]]])现在的输出包含3个通道,第一个通道的结果与先前输入张量X和多输入单输出通道的结果一致。
4.3. 1×1卷积层
1×1卷积,即kh=kw=1,看起来似乎没有多大意义。 毕竟,卷积的本质是有效提取相邻像素间的相关特征,而1×1卷积显然没有此作用。 尽管如此,1×1仍然十分流行,经常包含在复杂深层网络的设计中。
因为使用了最小窗口, 1 × 1 1\times 1 1×1卷积失去了卷积层的特有能力——在高度和宽度维度上,识别相邻元素间相互作用的能力。
其实 1 × 1 1\times 1 1×1卷积的唯一计算发生在通道上。
下图展示了使用 1 × 1 1\times 1 1×1卷积核与 3 3 3个输入通道和 2 2 2个输出通道的互相关计算。
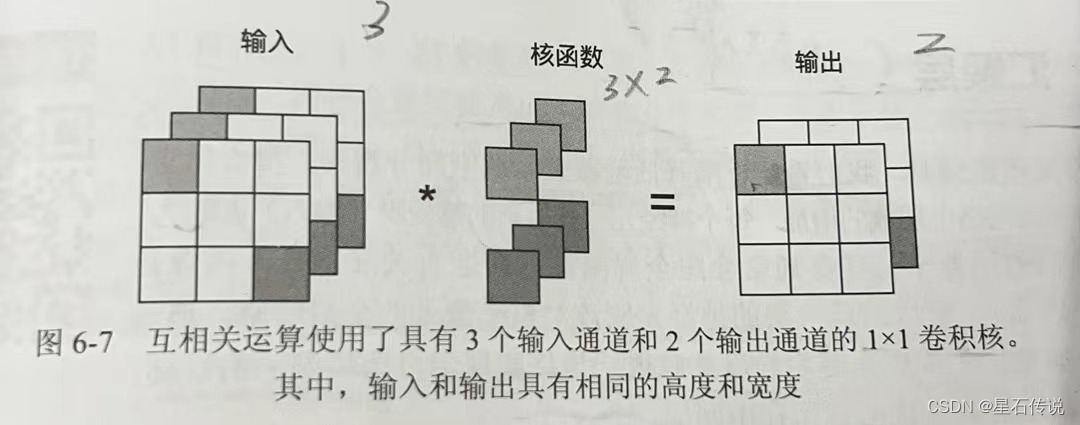
这里输入和输出具有相同的高度和宽度,输出中的每个元素都是从输入图像中同一位置的元素的线性组合。
我们可以将 1 × 1 1\times 1 1×1卷积层看作在每个像素位置应用的全连接层,以 c i c_i ci个输入值转换为 c o c_o co个输出值。
因为这仍然是一个卷积层,所以跨像素的权重是一致的。
同时, 1 × 1 1\times 1 1×1卷积层需要的权重维度为 c o × c i c_o\times c_i co×ci,再额外加上一个偏置。
下面,我们使用全连接层实现 1 × 1 1 \times 1 1×1卷积。请注意,我们需要对输入和输出的数据形状进行调整。
# 1x1卷积层
def corr2d_multi_in_out_1x1(X,K):c_i,h, w = X.shapec_o = K.shape[0]X = X.reshape((c_i,h*w)) #将每个通道的空间维度展平为一个列向量K = K.reshape((c_o,c_i))#全连接层中的矩阵乘法y = torch.matmul(K,X)return y.reshape(c_o,h,w) #恢复输出矩阵的通道数和空间维度#当执行1×1卷积运算时,上述函数相当于先前实现的互相关函数corr2d_multi_in_out。
X= torch.normal(0,1,(3,3,3))
K = torch.normal(0,1,(2,3,1,1))
y1 = corr2d_multi_in_out_1x1(X,K)
y2 = corr2d_multi_in_out(X,K)
print(y1);print(y2)
assert float(torch.abs(y1-y2).sum()) < 1e-6#结果:
tensor([[[ 0.5941, -0.5362, -1.0132],[ 1.8299, -1.2045, 1.1347],[-0.4486, -2.2969, -0.8045]],[[ 0.3476, 1.7180, 1.9936],[ 1.3062, 0.8710, 2.2610],[ 1.6681, -1.8917, -0.0728]]])
tensor([[[ 0.5941, -0.5362, -1.0132],[ 1.8299, -1.2045, 1.1347],[-0.4486, -2.2969, -0.8045]],[[ 0.3476, 1.7180, 1.9936],[ 1.3062, 0.8710, 2.2610],[ 1.6681, -1.8917, -0.0728]]])4.4. 小结
- 多输入多输出通道可以用来扩展卷积层的模型。
- 当以每像素为基础应用时, 1 × 1 1\times 1 1×1卷积层相当于全连接层。
- 1 × 1 1\times 1 1×1卷积层通常用于调整网络层的通道数量和控制模型复杂性。
总结
本章学习了填充和步幅这两个调整数据维度的应用原理,再就是学习了多输入与多输出通道的扩展卷积层模型的概念,以及1×1卷积层在调整通道数量上的运用。
下士闻道,大笑之──不笑,不足以为道。
–2023-10-12 进阶篇
相关文章:

深度学习——卷积神经网络(CNN)基础二
深度学习——卷积神经网络(CNN)基础二 文章目录 前言三、填充和步幅3.1. 填充3.2. 步幅3.3. 小结 四、多输入多输出通道4.1. 多输入通道4.2. 多输出通道4.3. 11卷积层4.4. 小结 总结 前言 上文对卷积有了初步的认识,其实卷积操作就是通过卷积…...
R语言进度条:txtProgressBar功能使用方法
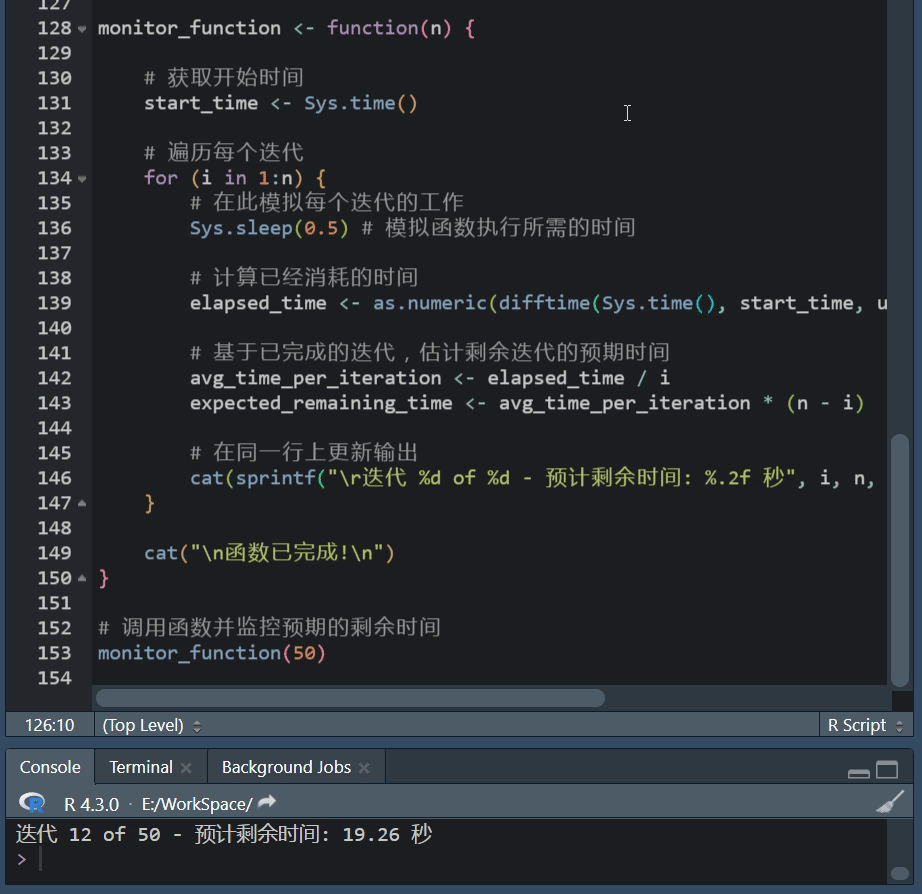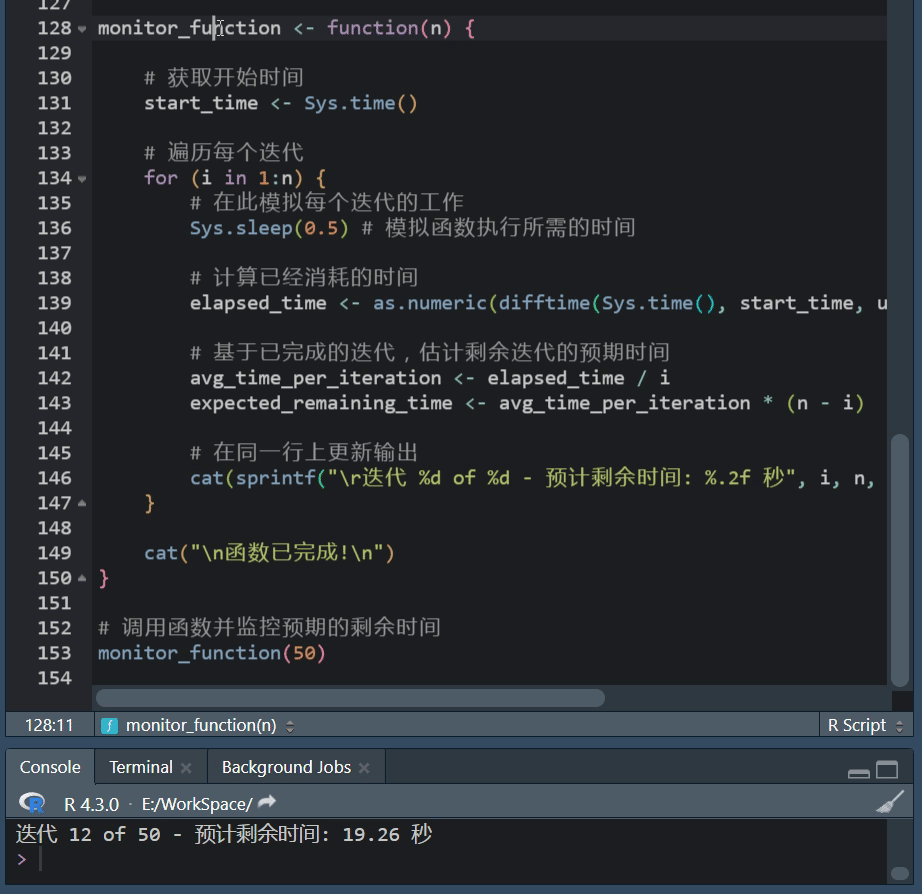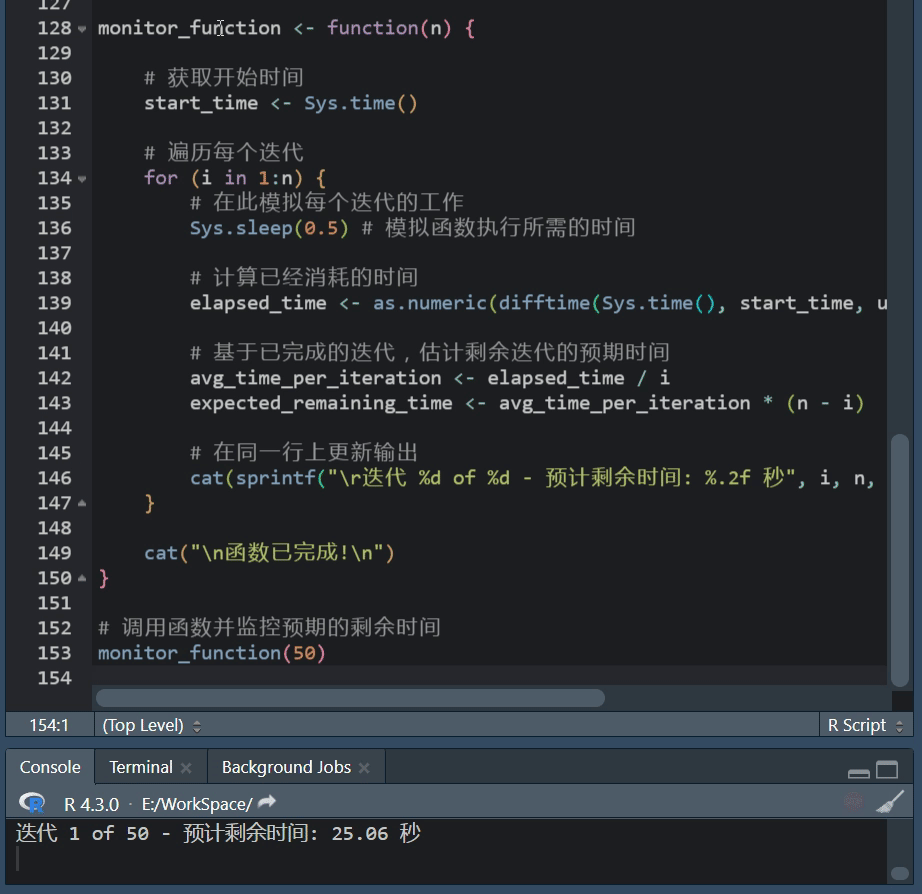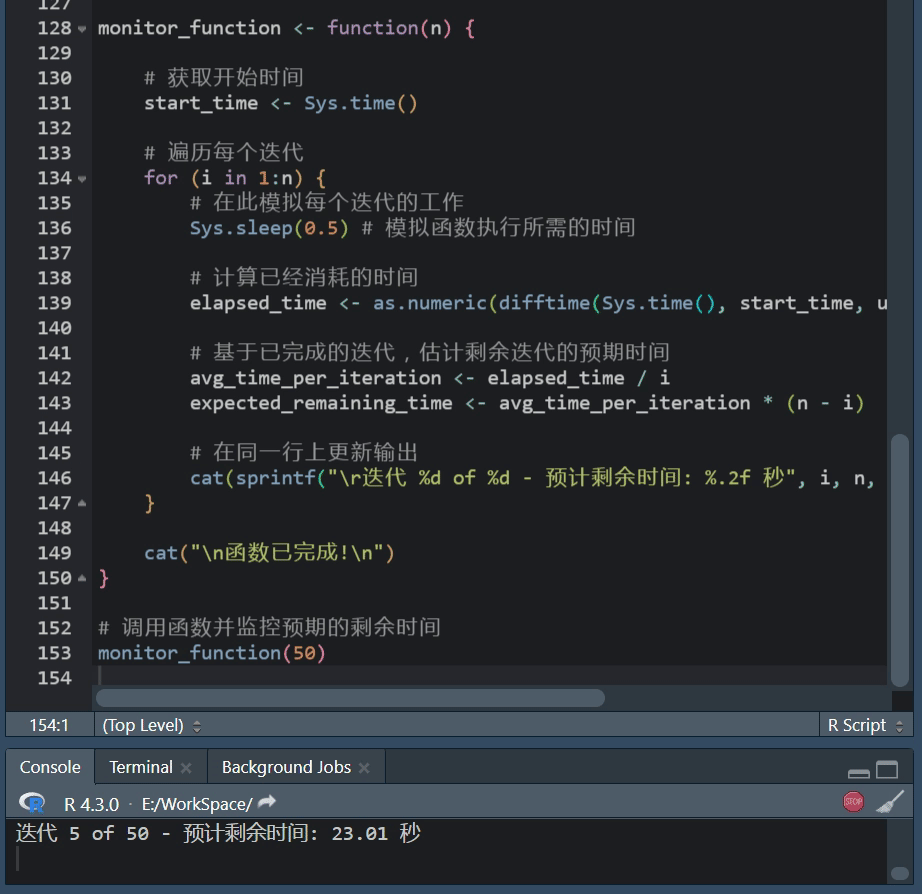
R语言进度条使用攻略 在数据处理、建模或其他计算密集型任务中,我们常常会执行一些可能需要很长时间的操作。 在这些情况下,展示一个进度条可以帮助我们了解当前任务的进度,以及大约还需要多长时间来完成,R语言提供了几种简单且灵…...

Maven实战-声明周期和插件
Maven实战-声明周期和插件 Maven 设计了插件机制,每个构建步骤都可以绑定一个或者多个插件行为,而且 Maven 为大多数构建步骤编写 并绑定了默认插件。例如,针对编译的插件有 maven-compiler-plugin,针对测试的插件有 maven-sure…...
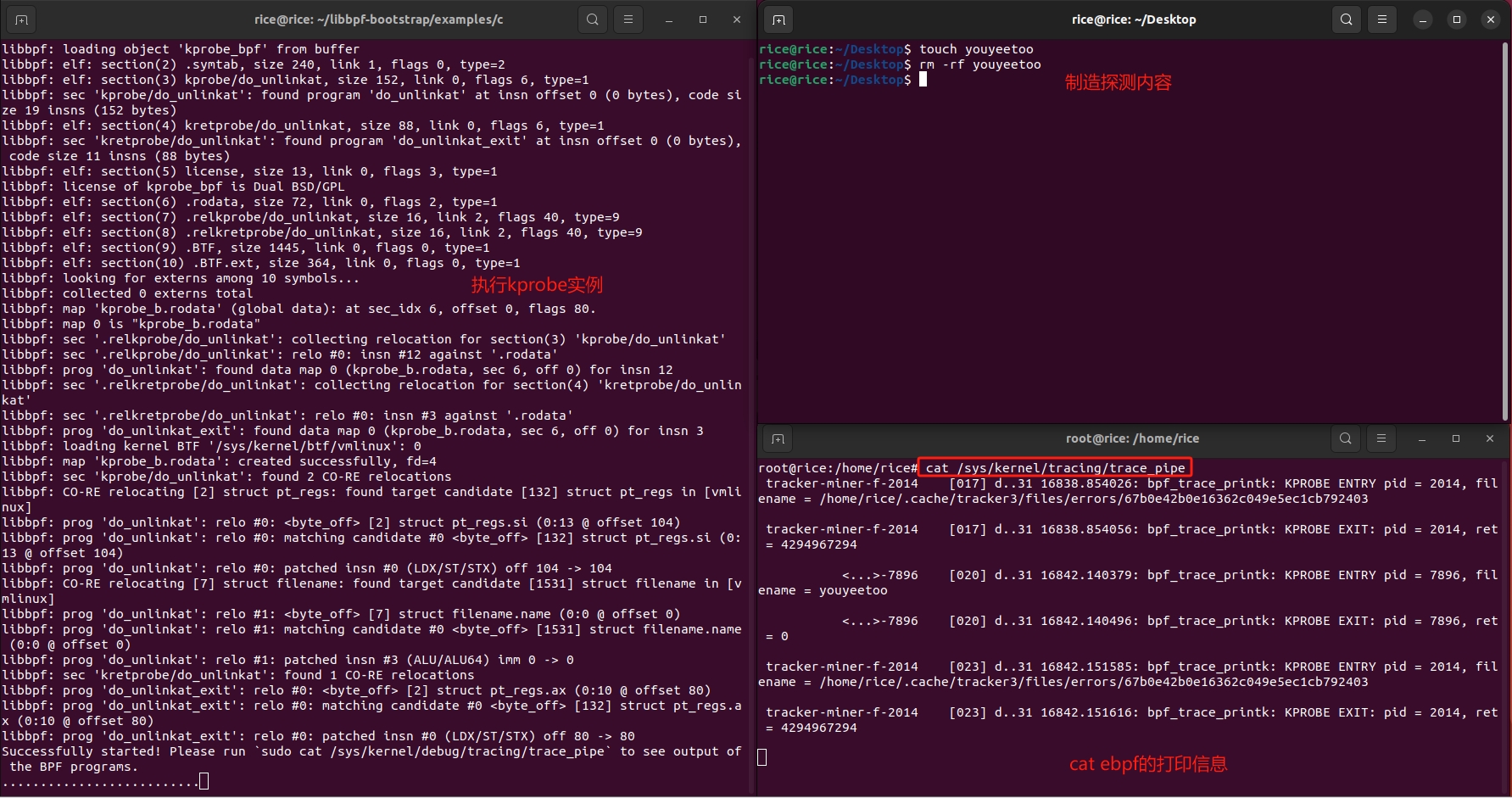
ebpf的快速开发工具--libbpf-bootstrap
基于ubuntu22.04-深入浅出 eBPF 基于ebpf的性能工具-bpftrace 基于ebpf的性能工具-bpftrace脚本语法 基于ebpf的性能工具-bpftrace实战(内存泄漏) 什么是libbpf-bootstrap libbpf-bootstrap是一个开源项目,旨在帮助开发者快速启动和开发使用eBPF(Extended Berk…...

万界星空科技/生产制造执行MES系统/开源MES/免费MES
开源系统概述: 万界星空科技免费MES、开源MES、商业开源MES、市面上最好的开源MES、MES源代码、免费MES、免费智能制造系统、免费排产系统、免费排班系统、免费质检系统、免费生产计划系统、免费数字化大屏。 万界星空开源MES制造执行系统的Java开源版本。开源mes…...

螺纹快速接头在卫浴行业中的应用提高产量降低生产成本
螺纹快速接头在卫浴行业主要用于上下水测试和密封性测试,可以快速密封连接待测产品和水管。取代之前的工人手拧编织管六角螺母的方式,方便快捷,密封性好,产品测试更稳定。 卫浴行业产品必须具备很好的密封性,防止在实际…...
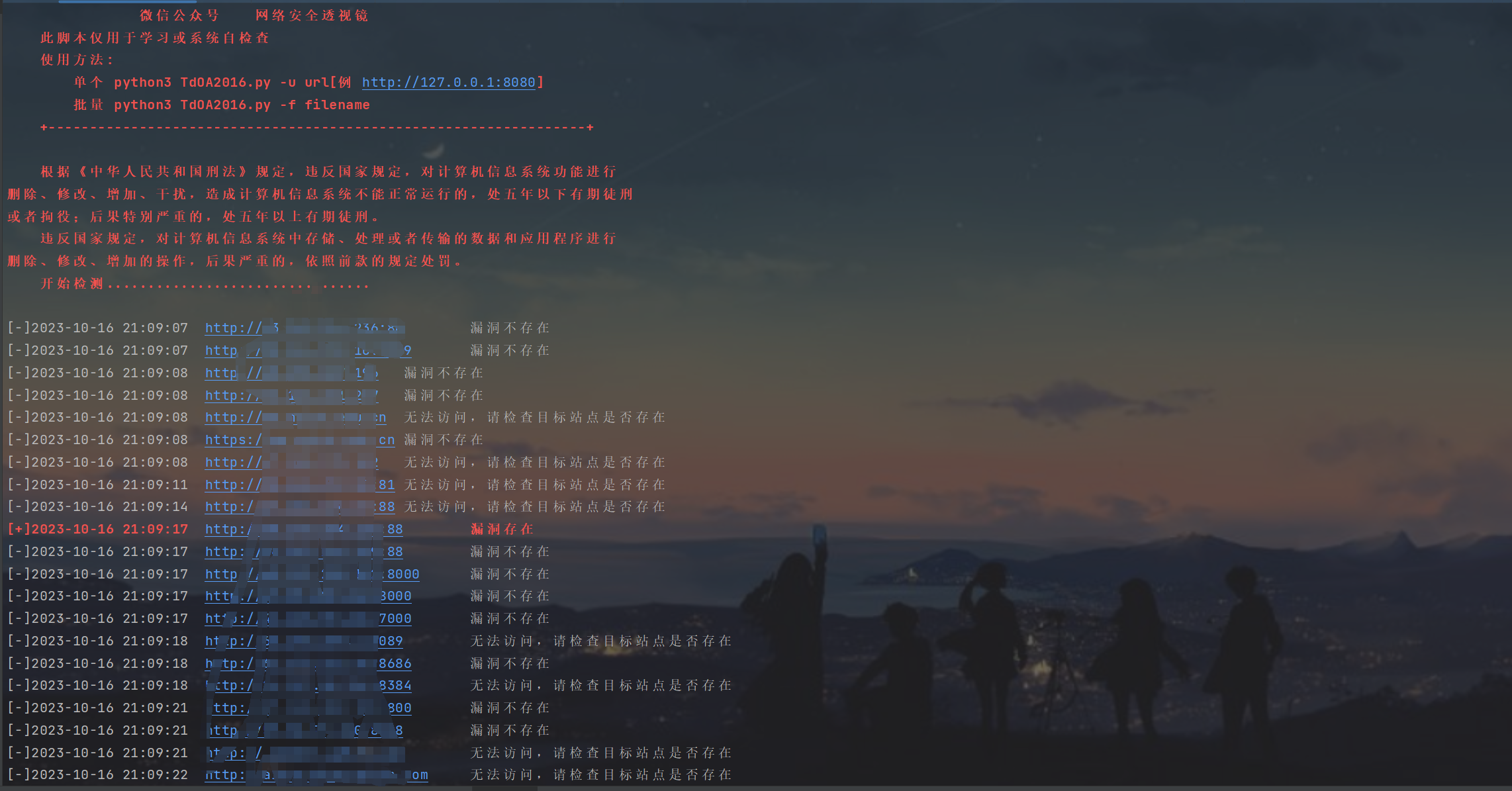
通达OA 2016网络智能办公系统 handle.php SQL注入漏洞
一、漏洞描述 北京通达信科科技有限公司通达OA2016网络智能办公系统 handle.php 存在sql注入漏洞,攻击者可利用此漏洞获取数据库管理员权限,查询数据、获取系统信息,威胁企业单位数据安全。 二、网络空间搜索引擎查询 fofa查询 app"T…...

parameter的各种用法以及localparam的用法
parameter的各种用法以及localparam的用法 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 module para_local();parameter a 10; // 第一种用法 parameter a 4d10; // 第二种用法 para…...

网络社区挖掘-图论部分的基本知识笔记
1 网络社区挖掘定义 网络社区挖掘是指利用数据挖掘技术和机器学习算法,分析社交网络、在线社区或互联网上的各种交互数据,以揭示其中隐藏的模式、关系和信息。这些社区可以是社交媒体平台、在线论坛、博客、微博等,人们在这些平台上进行交流…...

Vue Router - 路由的使用、两种切换方式、两种传参方式、嵌套方式
目录 一、Vue Router 1.1、下载 1.2、基本使用 a)引入 vue-router.js(注意:要在 Vue.js 之后引入). b)创建好路由规则 c)注册到 Vue 实例中 d)展示路由组件 1.3、切换路由的两种方式 1.…...

mysql为什么会选错索引,以及优化器是如何选择索引的
一:概念 在 索引建立之后,一条语句可能会命中多个索引,这时,索引的选择,就会交由 优化器 来选择合适的索引。 优化器选择索引的目的,是找到一个最优的执行方案,并用最小的代价去执行语句。 二…...
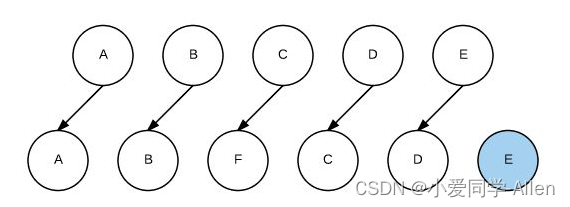
vue基础知识十七:你知道vue中key的原理吗?说说你对它的理解
一、Key是什么 开始之前,我们先还原两个实际工作场景 1.当我们在使用v-for时,需要给单元加上key <ul><li v-for"item in items" :key"item.id">...</li> </ul>2.用new Date()生成的时间戳作为key&#x…...
攻防演练蓝队|Windows应急响应入侵排查
文章目录 日志分析web日志windows系统日志 文件排查进程排查新增、隐藏账号排查启动项/服务/计划任务排查工具 日志分析 web日志 dirpro扫描目录,sqlmap扫描dvwa Python dirpro -u http://192.168.52.129 -b sqlmap -u "http://192.168.52.129/dvwa/vulnera…...

uniapp 小程序实现图片宽度100%、高度自适应的效果
因为image组件默认是有宽度跟高度的,所以这个高度不怎么好写 通过load事件来控制图片的高度 话不多说,直接上代码, <image class"img" src"/static/image.png" :style"{ height: imgHeight px }"mode&q…...

05. NXP官方SDK使用实验
05. NXP官方SDK使用实验 官方SDK移植 官方SDK移植 新建cc.h文件 SDK包里面会用到很多数据类型,所以需要在该文件中定义一些常用的数据类型 #pragma once #define __I volatile #define __O volatile #define __IO volatiletypedef sig…...

Python- JSON使用初探
JSON 在JSON格式中,{} 和 [] 是两种主要的数据结构,分别表示对象(或称为字典、哈希、map)和数组(或称为列表、序列)。 {} - 对象 在JSON中,对象是一组"key": value对的集合。这些键必…...

vim的配置文件
用户级别配置文件 ~/.vimrc 修改用户级别的配置文件只会影响当前用户, 不会影响其他的用户. 例如: 在用户的家目录下的.vimrc文件中添加 set tabstop4 ----设置缩进4个空格 set nu ----设置行号 set shiftwidth4 —设置ggG缩进4个空格, 默认是缩进8个空格 系统级别配置文件 /e…...
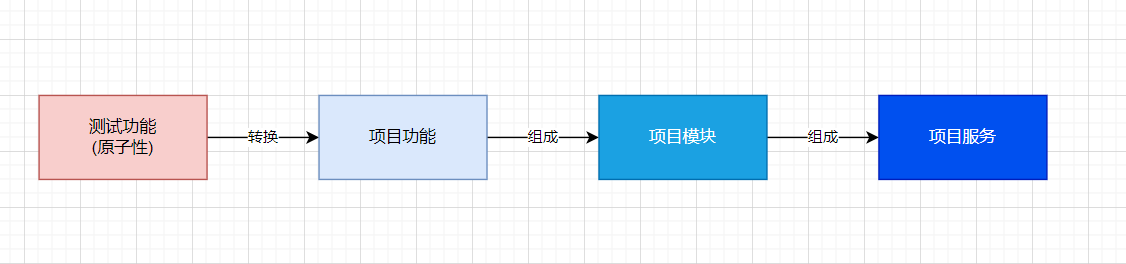
[python] pytest
在写一个项目前, 可以先编写测试模块 测试模块中包含了一个个最小的功能 当每一个功能都完善正确时 再将这些功能转换成项目运行的功能 多个项目运行的功能就组成了一个模块 多个模块就组成了一个项目服务 pytest 是一个 Python 测试框架,它提供了简单易用的语…...

【王道代码】【2.2顺序表】d1
关键字: 删除最小值最后位补齐;逆置;删除所有x;删除值为s到t区间的元素...

【Linux】【创建文件】Linux系统下在命令行中创建文件的方法
🐚作者简介:花神庙码农(专注于Linux、WLAN、TCP/IP、Python等技术方向)🐳博客主页:花神庙码农 ,地址:https://blog.csdn.net/qxhgd🌐系列专栏:Linux技术&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
