【数据结构】排序--插入排序(希尔排序)
目录
一 基本思想
二 直接插入排序
三 希尔排序
一 基本思想
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想
二 直接插入排序
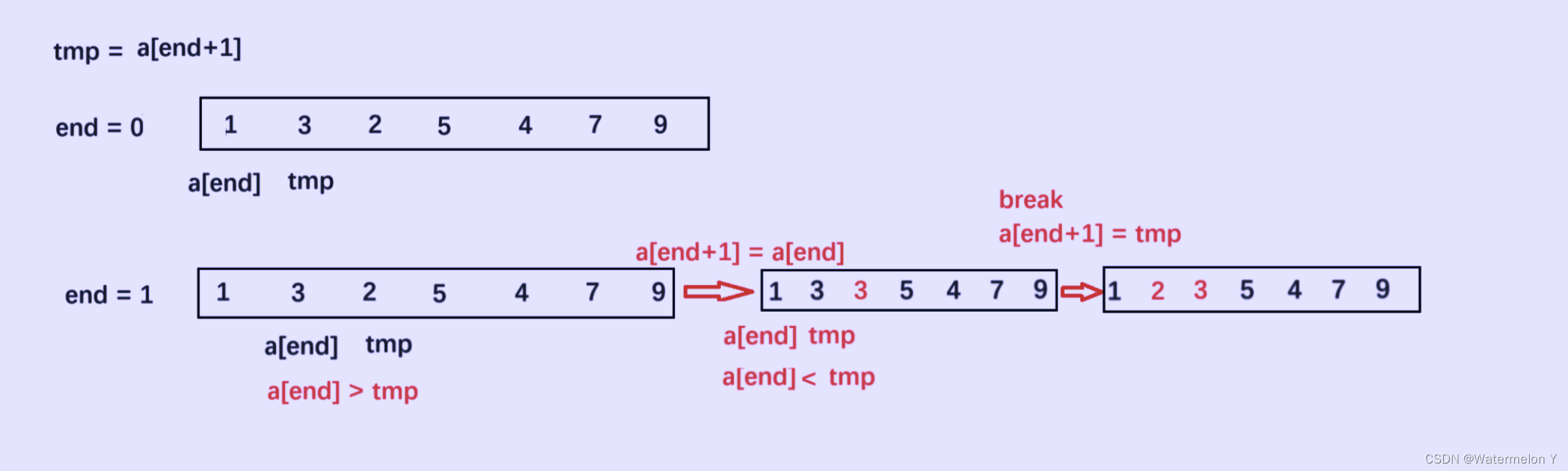
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与 array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N ^ 2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
#include<stdio.h>
void InsertSort(int* a, int n)
{int i = 0;for (i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;//因为前面end--了 所以这里是a[end+1]}
}
int main()
{int arr[] = { 1, 3, 2, 5, 4, 7, 9 };InsertSort(arr, sizeof(arr) / sizeof(int));//排升序for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}
}
三 希尔排序
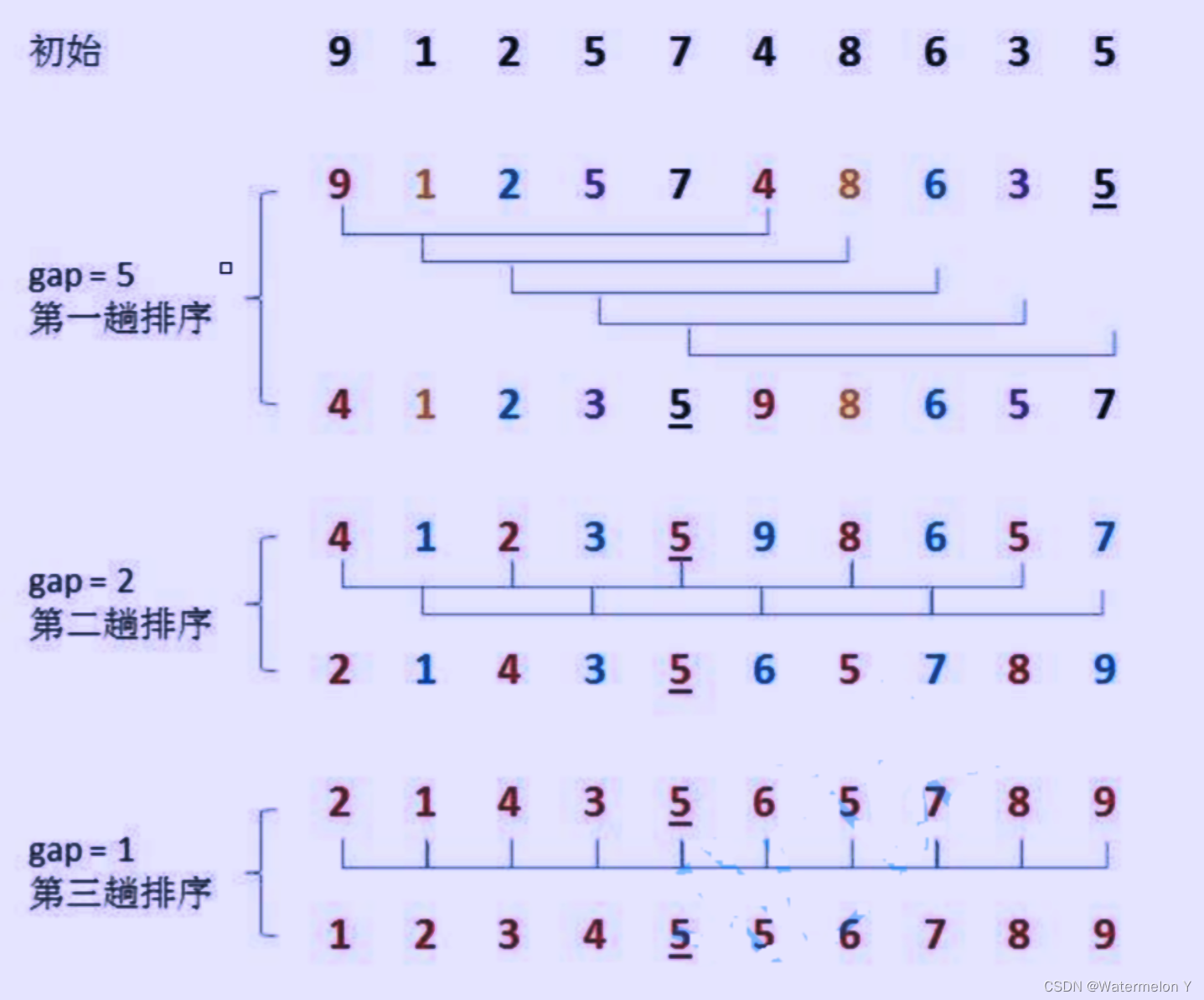
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个n 组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后,取重复上述分组和排序的工作。当到达gap == 1时,所有记录在统一组内排好序。
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap /= 2;gap = gap / 3 + 1;//这样可以更快//直接插入排序思想for (int i = 0; i < n- gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}int main()
{int arr[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5};//InsertSort(arr, sizeof(arr) / sizeof(int));//排升序InsertSort(arr, sizeof(arr) / sizeof(int));//排升序for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}
}

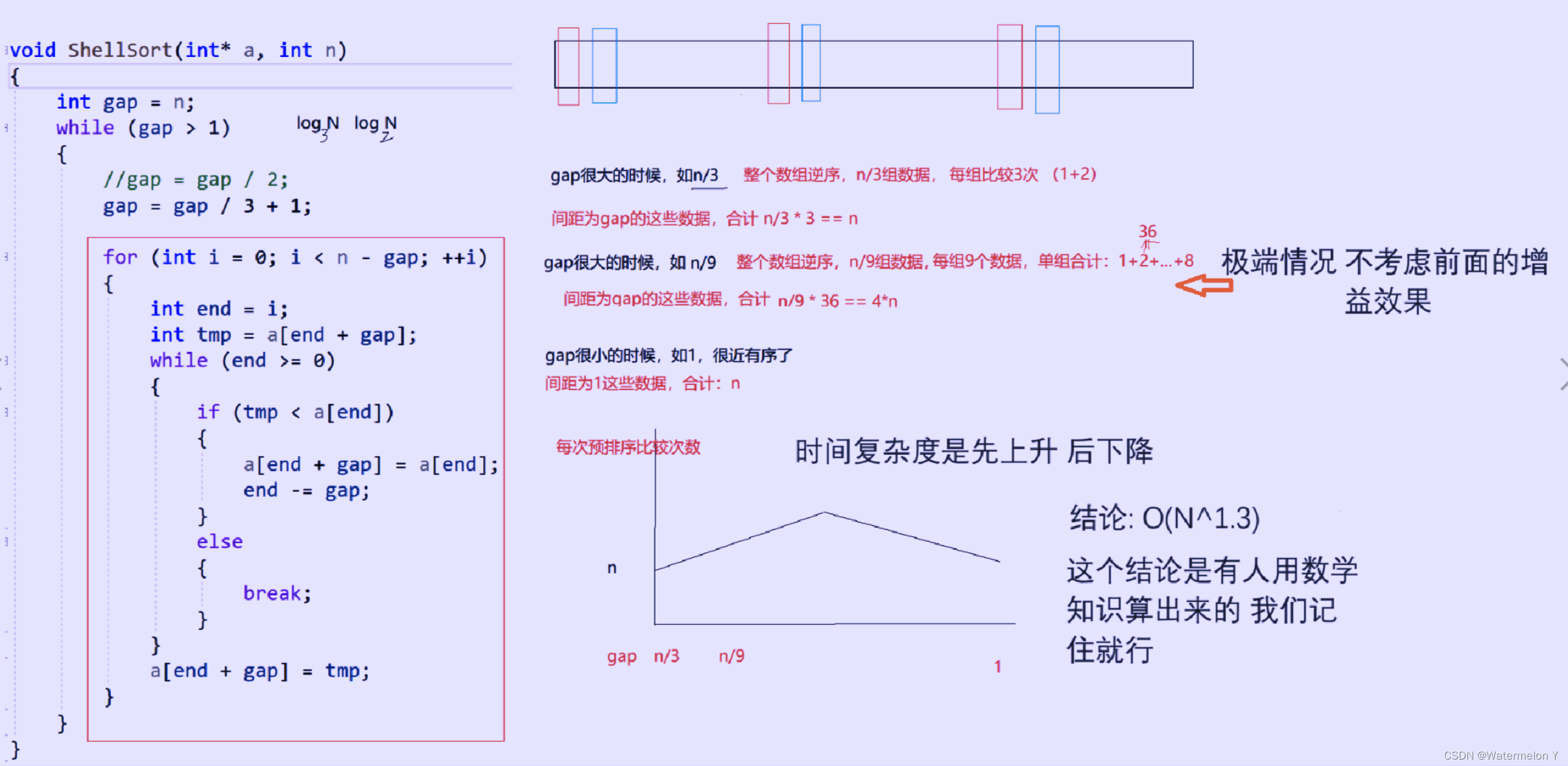
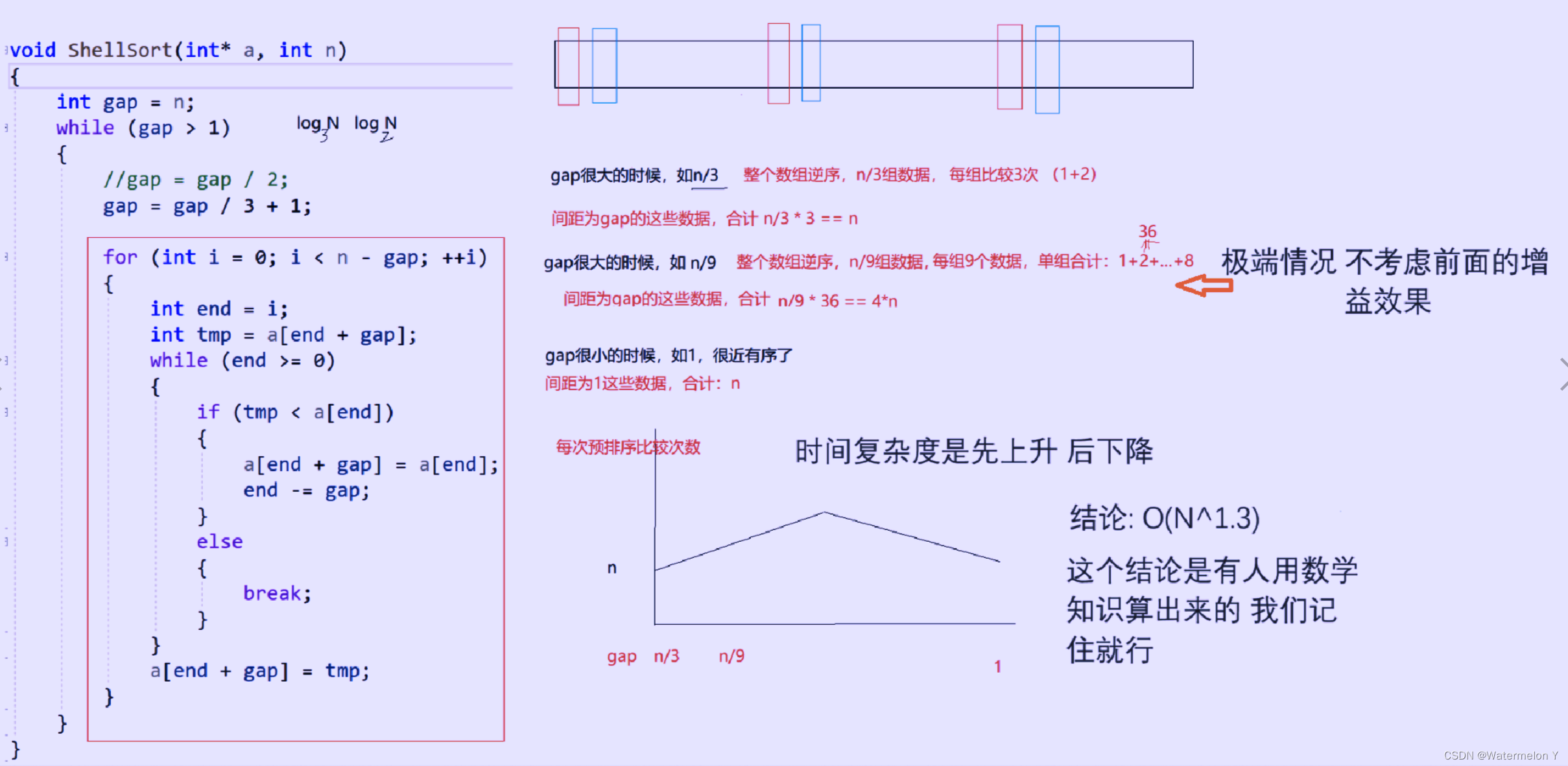
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就 会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的 希尔排序的时间复杂度都不固定
4. 稳定性:不稳定
本节的重难点是希尔排序, 希尔排序实际上就是直接插入排序的优化, 只要理解了直接插入排序, 希尔排序就不难了.大家可以根据图解和代码进行实操.
继续加油!
相关文章:

【数据结构】排序--插入排序(希尔排序)
目录 一 基本思想 二 直接插入排序 三 希尔排序 一 基本思想 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想 二…...

“探寻服务器的无限潜能:从创意项目到在线社区,你会做什么?”
文章目录 每日一句正能量前言什么是服务器?服务器能做什么?服务器怎么用?部署创意项目,还是在线社区亦或做其他的?后记 每日一句正能量 未知的下一秒,千万不要轻言放弃。 前言 在数字化时代,服…...
5年经验之谈 —— 深入了解性能测试:方法、工具和最佳实践!
性能测试是软件开发生命周期中至关重要的一部分,它有助于确保应用程序在不同负载条件下都能够高效运行。在竞争激烈的市场中,性能问题可能导致用户流失,损害声誉,并损害业务。本文将深入探讨性能测试的方法、工具和最佳实践&#…...
动态加载sprite是multiple模式(即该sprite包含了很多小图)里的小图
在Unity中,Resources.Load()方法可以用来加载资源。如果要加载Sprite下的multiple模式的图片,你需要知道这些图片的路径。 首先,你需要把你想要加载的资源放在一个名为"Resources"的文件夹内。然后,你可以使用以下代码…...
大数据 DataX 详细安装教程
目录 一、环境准备 二、安装部署 2.1 二进制安装 2.2 python 3 支持 三、Data X 初体验 3.1 配置示例 3.1.1. 生成配置模板 3.1.2 创建配置文件 3.1.3 运行 DataX 3.1.4 结果显示 3.2 动态传参 3.2.1. 动态传参的介绍 3.2.2. 动态传参的案例 3.3 迸发设置 …...
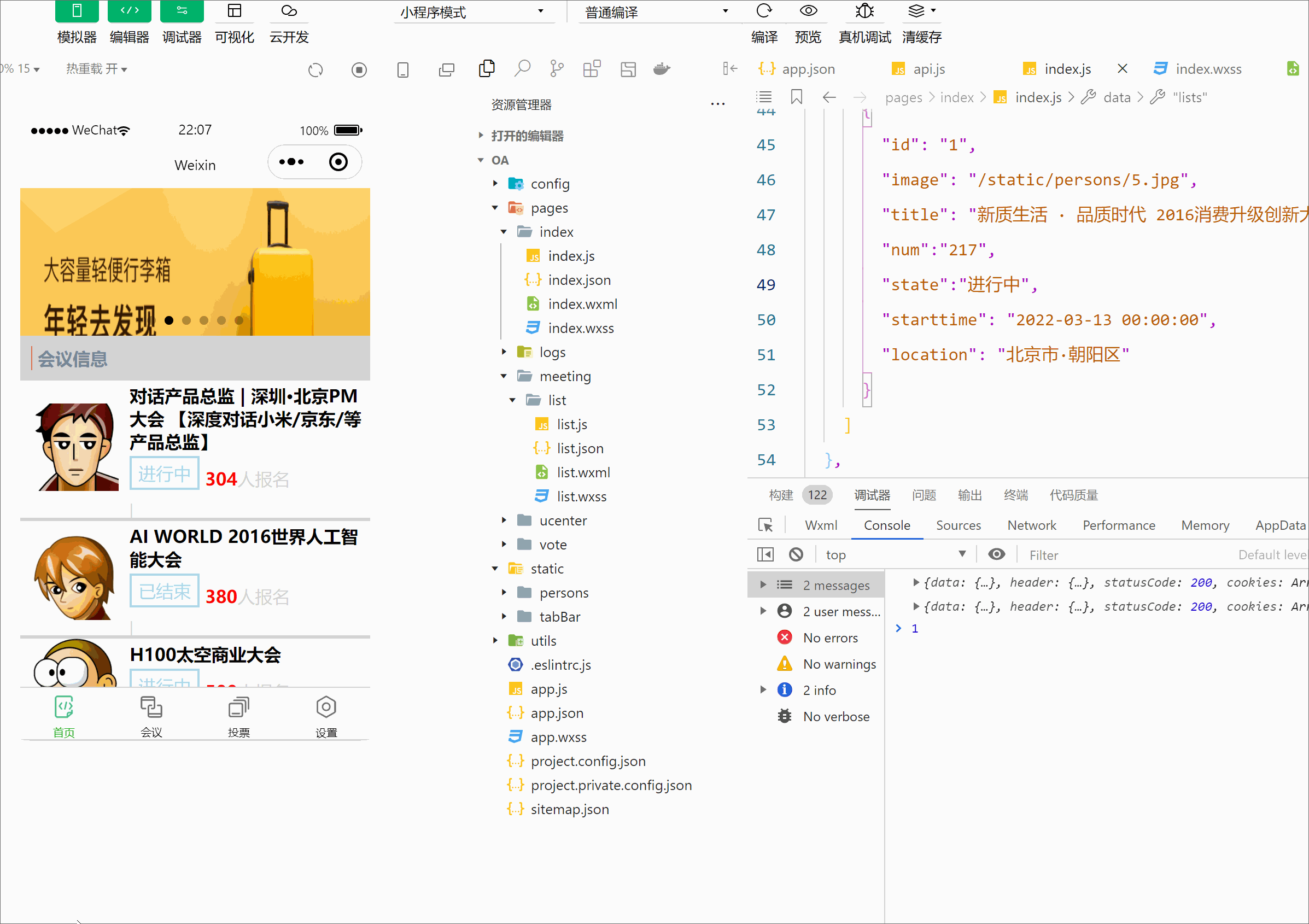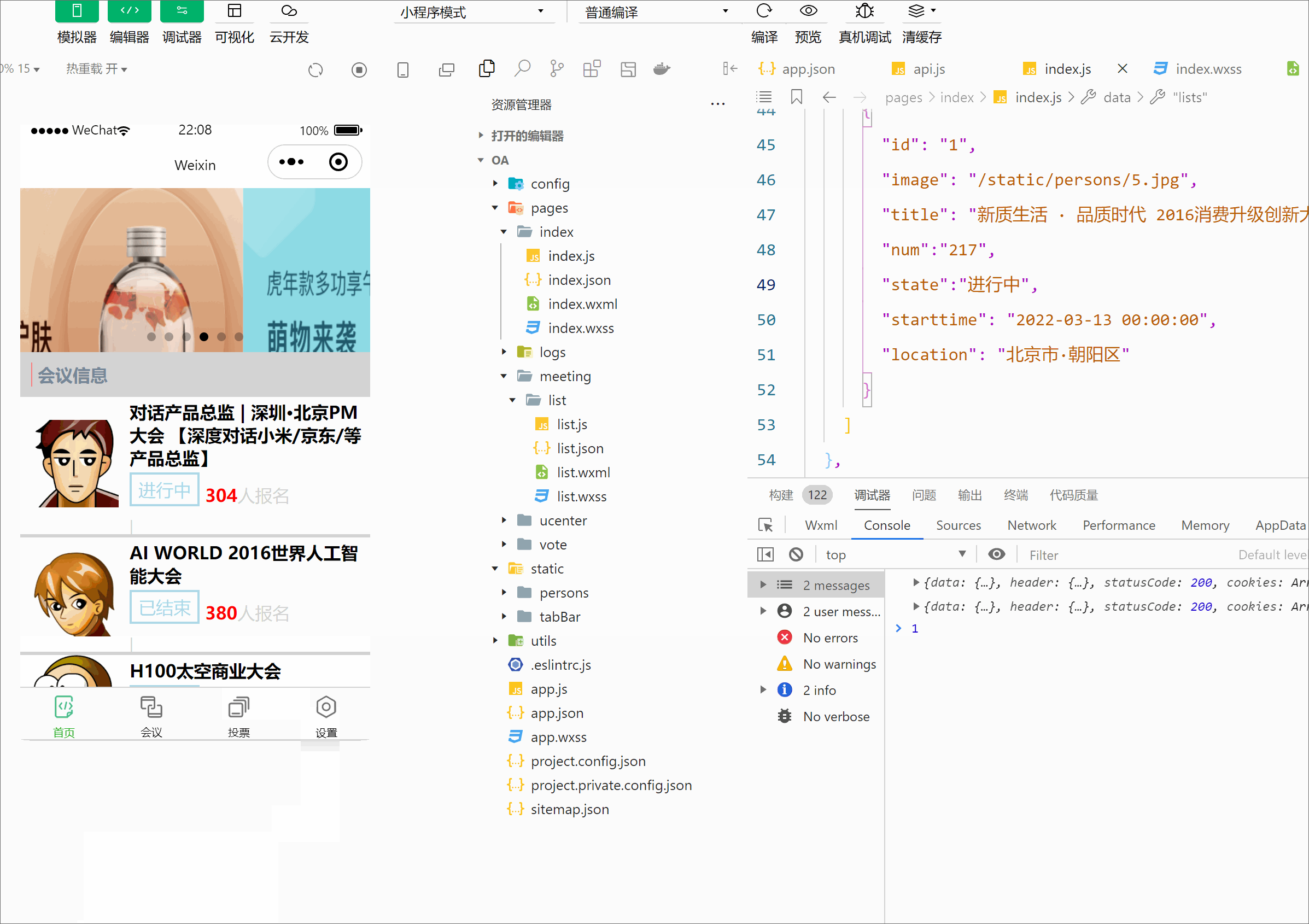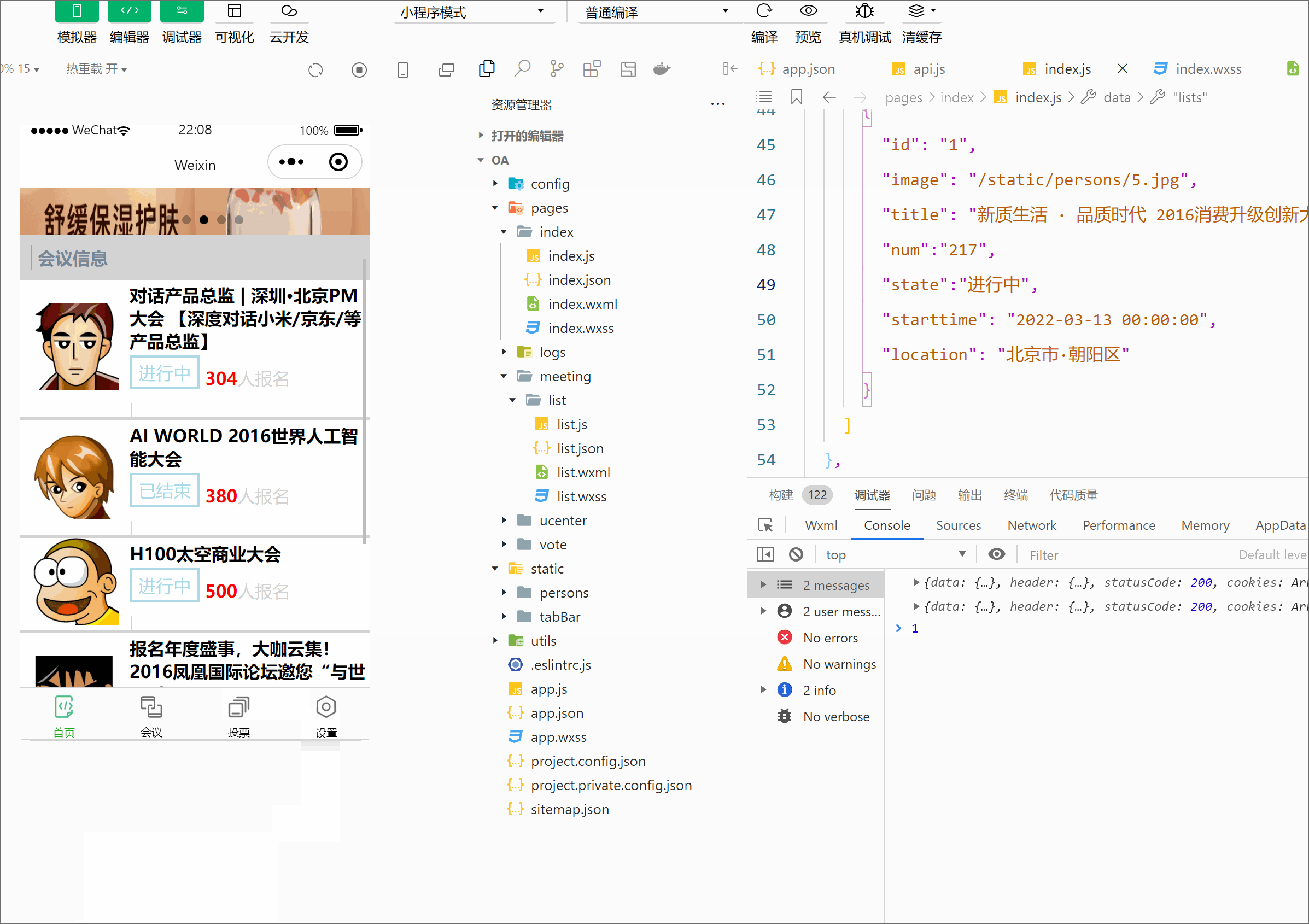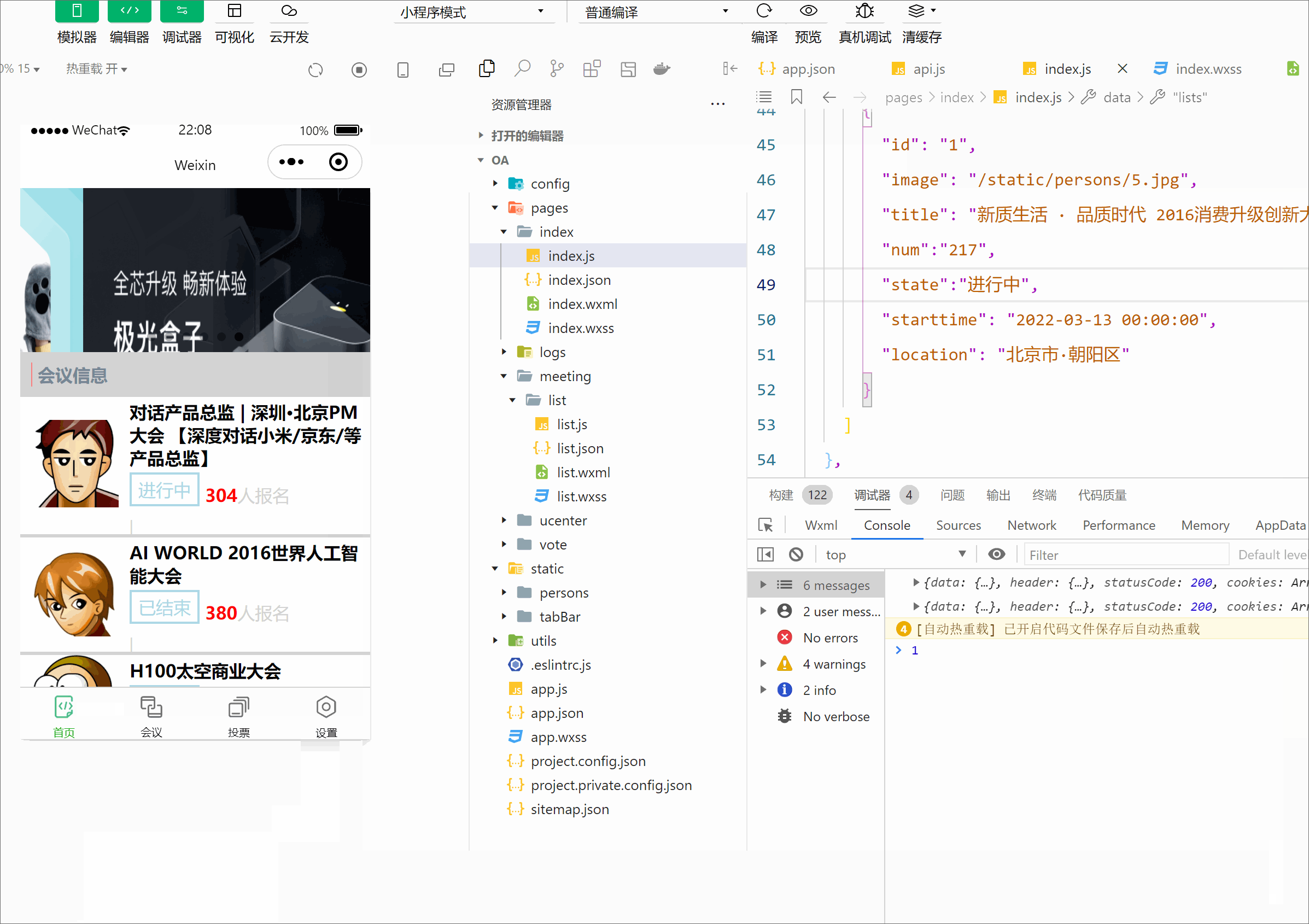
微信小程序开发之会议oa(首页搭建)
前言: 上一篇我们掌握了关于小程序的框架,这篇博客带你完成小程序版的会议OA首页。效果如下: 一, 1.1先创建OA首页页面: 首先我们先建一个新项目,在app.json中编写代码 {"pages": ["pages/…...

了解主启动类怎么运行
//SpringBootApplication 标注这个类是spring boot的应用,启动类下的所有资源都会被导入 SpringBootApplication public class SpringbootApplication { public static void main(String[] args) { //以为是启动了一个方法,没想到启动了一个服务 SpringA…...

【LeetCode】31. 下一个排列
1 问题 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地&a…...

支持语音与视频即时通讯项目杂记(一)
第一部分解释服务端的实现。 (服务端结构) 下面一个用于实现TCP服务器的代码,包括消息服务器(TcpMsgServer)和文件中转服务器(TcpFileServer)。 首先,TcpServer是TcpMsgServer和Tcp…...

文档:htm格式转txt
꧂ 两个地方都保存꧁ import os import codecs from bs4 import BeautifulSoupdef generate_output_filename(file_path, save_path):# 获取文件名(不包含扩展名)file_name os.path.splitext(os.path.basename(file_path))[0]# 构造保存路径和文件名ou…...

电子邮件地址注册过程详解
许多人可能对如何注册电子邮件地址感到困惑,本文将详细解析电子邮件地址的注册过程:确定邮箱厂商、创建邮箱账户、设置电子邮件地址。 1、确定要注册的邮箱厂商 首先我们需要确定要注册哪种类型的电子邮件服务。目前市场上有许多不同的电子邮件服务提供商…...
深度学习——卷积神经网络(CNN)基础二
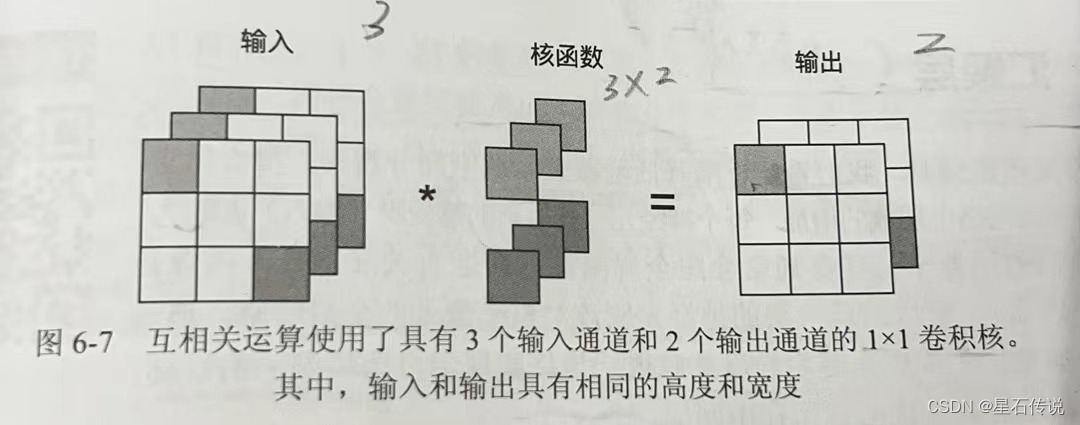
深度学习——卷积神经网络(CNN)基础二 文章目录 前言三、填充和步幅3.1. 填充3.2. 步幅3.3. 小结 四、多输入多输出通道4.1. 多输入通道4.2. 多输出通道4.3. 11卷积层4.4. 小结 总结 前言 上文对卷积有了初步的认识,其实卷积操作就是通过卷积…...
R语言进度条:txtProgressBar功能使用方法
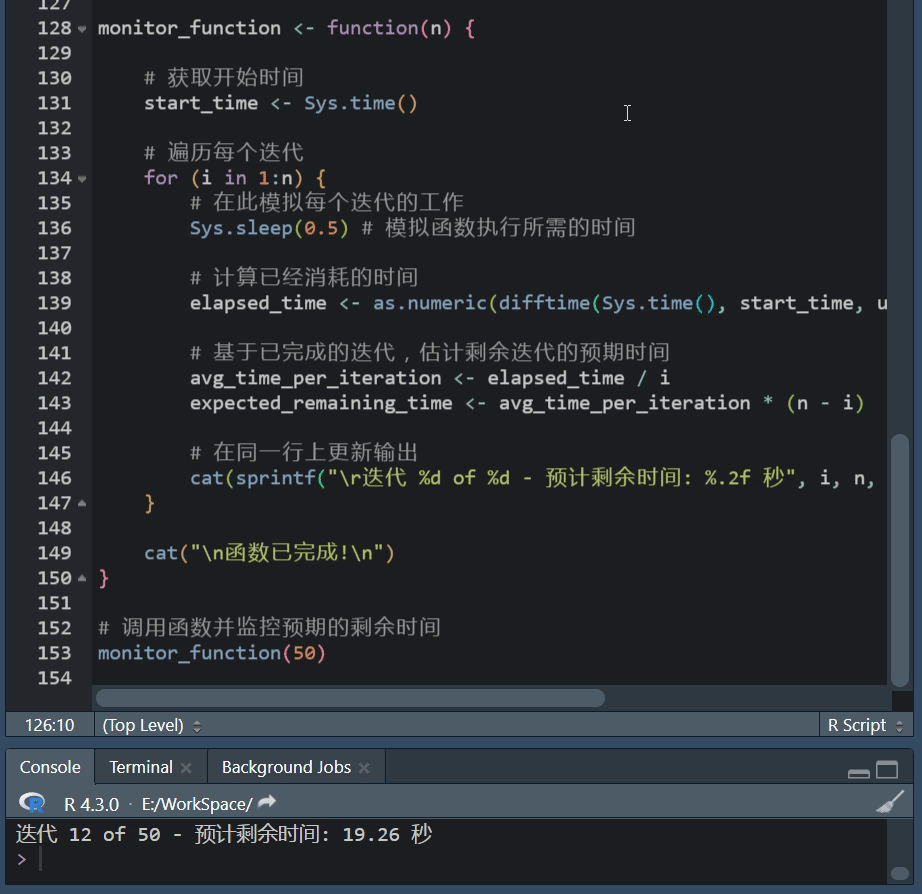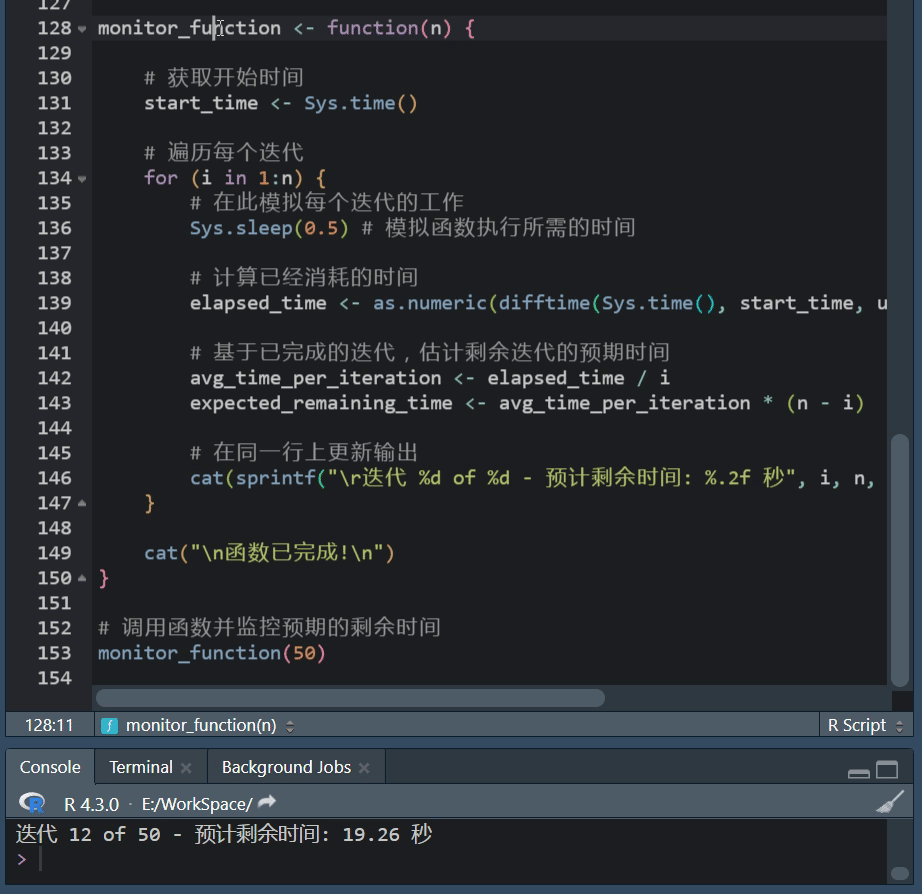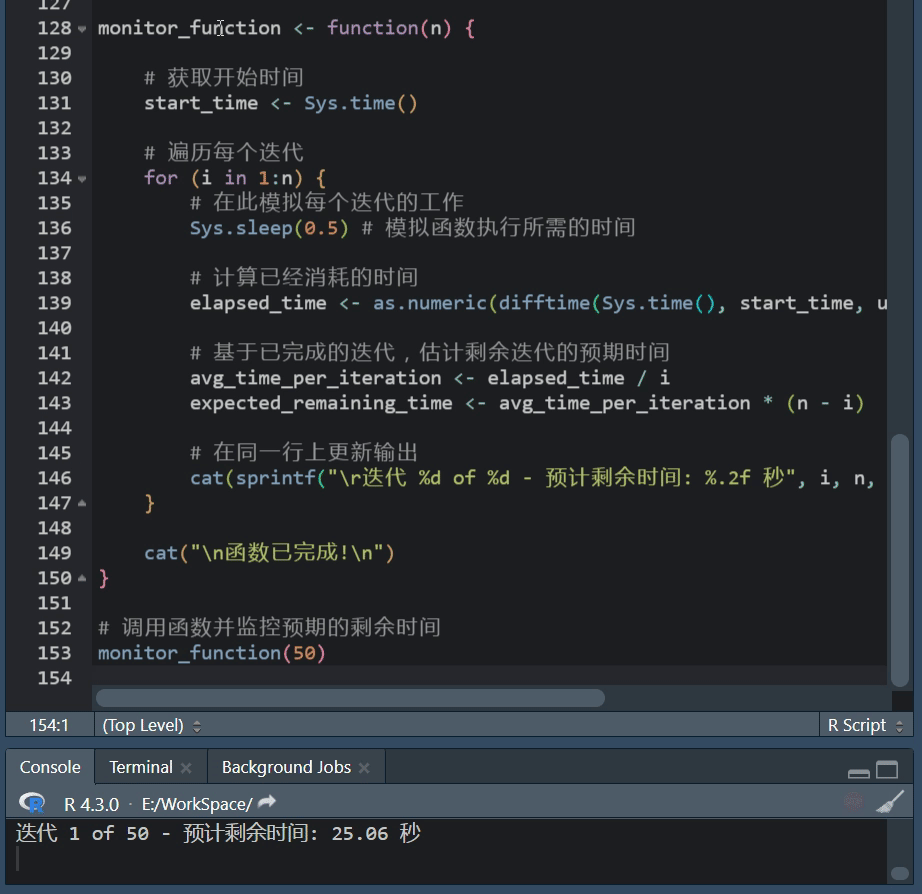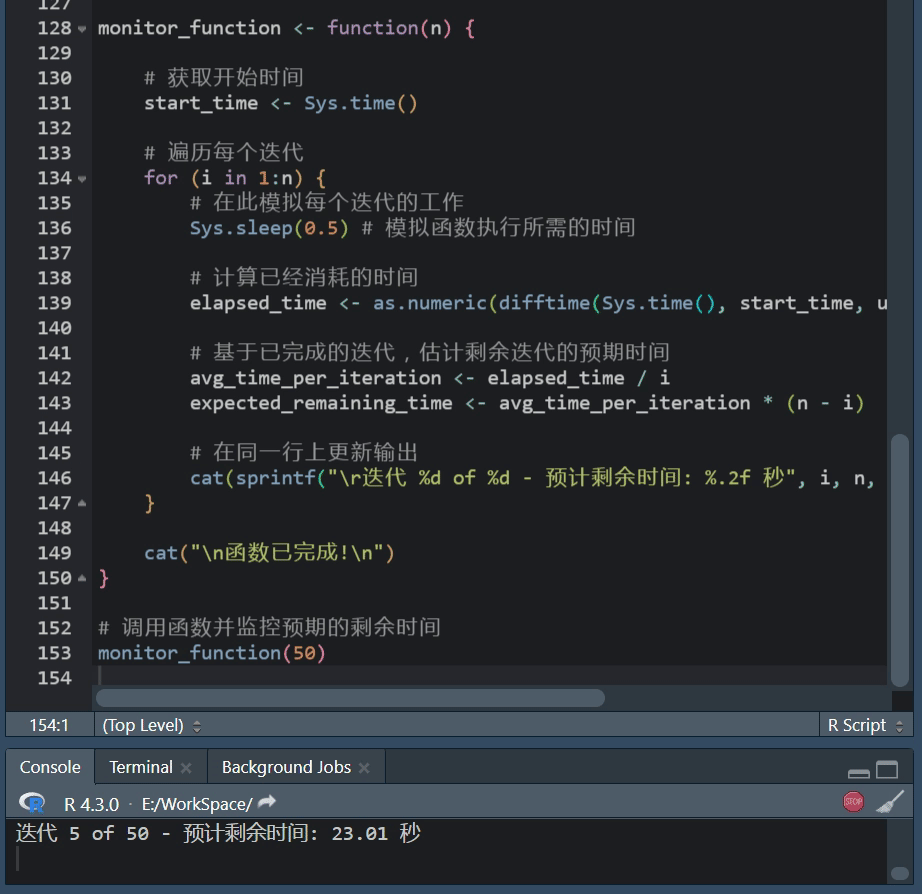
R语言进度条使用攻略 在数据处理、建模或其他计算密集型任务中,我们常常会执行一些可能需要很长时间的操作。 在这些情况下,展示一个进度条可以帮助我们了解当前任务的进度,以及大约还需要多长时间来完成,R语言提供了几种简单且灵…...

Maven实战-声明周期和插件
Maven实战-声明周期和插件 Maven 设计了插件机制,每个构建步骤都可以绑定一个或者多个插件行为,而且 Maven 为大多数构建步骤编写 并绑定了默认插件。例如,针对编译的插件有 maven-compiler-plugin,针对测试的插件有 maven-sure…...
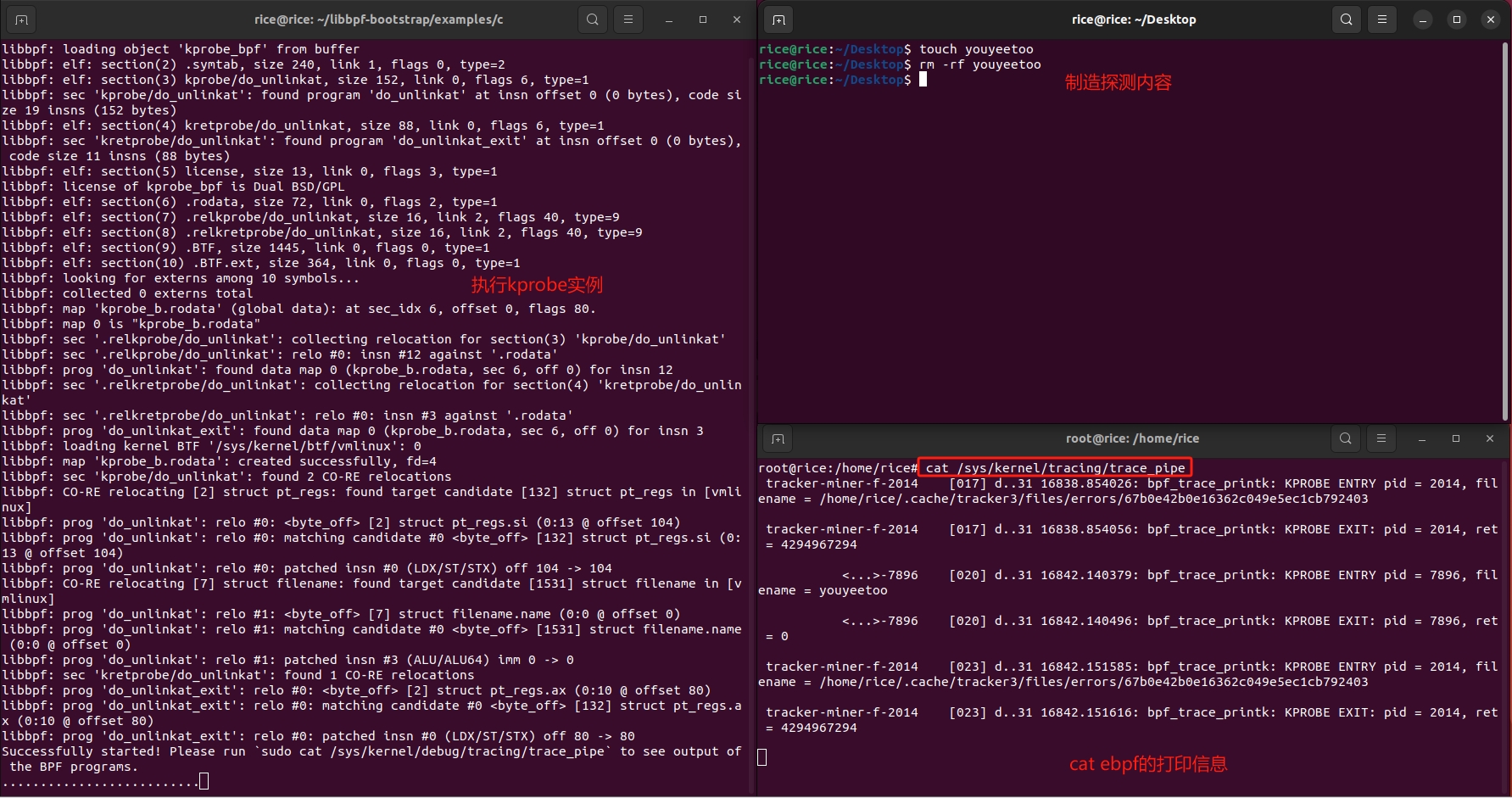
ebpf的快速开发工具--libbpf-bootstrap
基于ubuntu22.04-深入浅出 eBPF 基于ebpf的性能工具-bpftrace 基于ebpf的性能工具-bpftrace脚本语法 基于ebpf的性能工具-bpftrace实战(内存泄漏) 什么是libbpf-bootstrap libbpf-bootstrap是一个开源项目,旨在帮助开发者快速启动和开发使用eBPF(Extended Berk…...

万界星空科技/生产制造执行MES系统/开源MES/免费MES
开源系统概述: 万界星空科技免费MES、开源MES、商业开源MES、市面上最好的开源MES、MES源代码、免费MES、免费智能制造系统、免费排产系统、免费排班系统、免费质检系统、免费生产计划系统、免费数字化大屏。 万界星空开源MES制造执行系统的Java开源版本。开源mes…...

螺纹快速接头在卫浴行业中的应用提高产量降低生产成本
螺纹快速接头在卫浴行业主要用于上下水测试和密封性测试,可以快速密封连接待测产品和水管。取代之前的工人手拧编织管六角螺母的方式,方便快捷,密封性好,产品测试更稳定。 卫浴行业产品必须具备很好的密封性,防止在实际…...
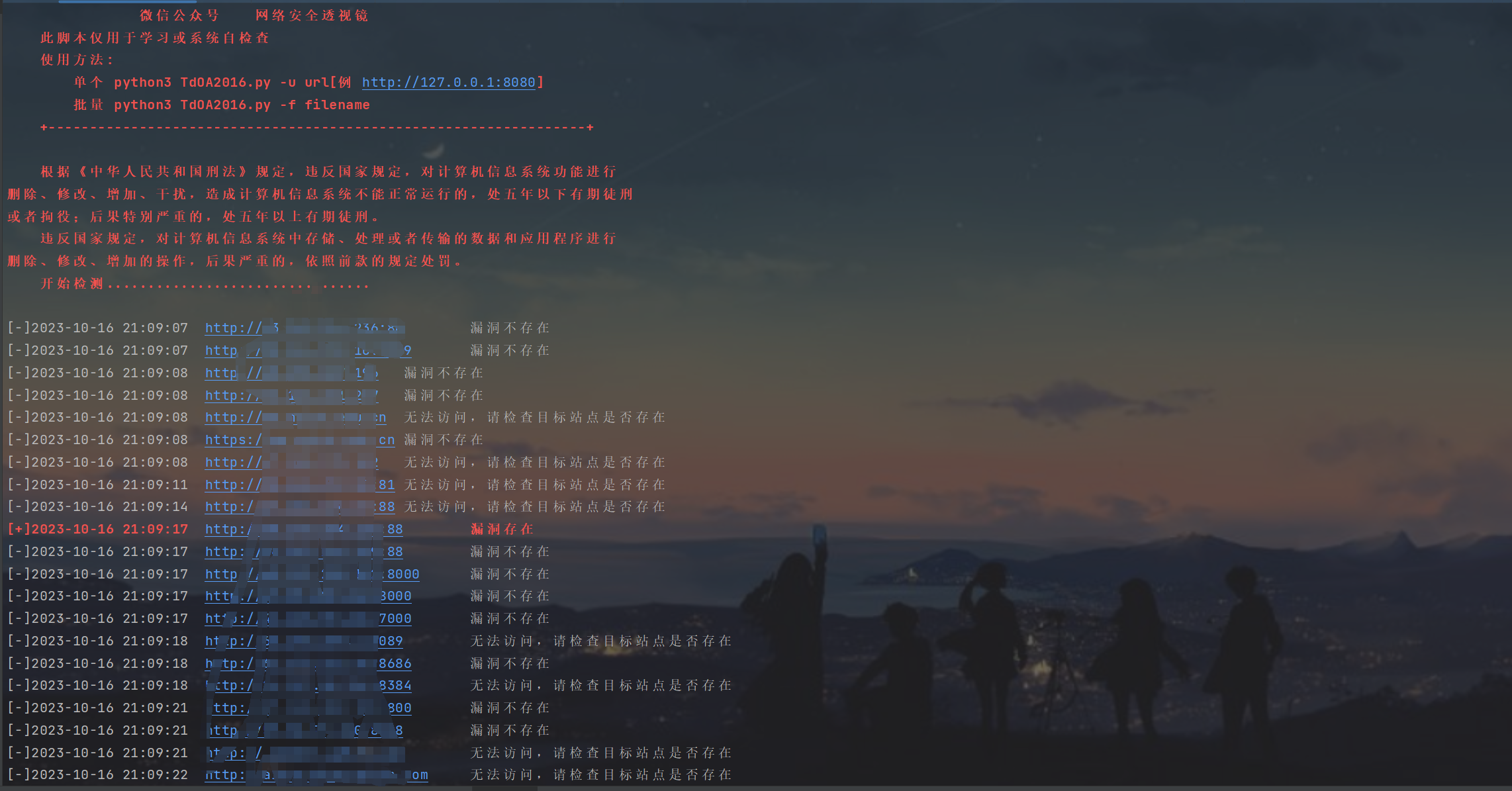
通达OA 2016网络智能办公系统 handle.php SQL注入漏洞
一、漏洞描述 北京通达信科科技有限公司通达OA2016网络智能办公系统 handle.php 存在sql注入漏洞,攻击者可利用此漏洞获取数据库管理员权限,查询数据、获取系统信息,威胁企业单位数据安全。 二、网络空间搜索引擎查询 fofa查询 app"T…...

parameter的各种用法以及localparam的用法
parameter的各种用法以及localparam的用法 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 module para_local();parameter a 10; // 第一种用法 parameter a 4d10; // 第二种用法 para…...

网络社区挖掘-图论部分的基本知识笔记
1 网络社区挖掘定义 网络社区挖掘是指利用数据挖掘技术和机器学习算法,分析社交网络、在线社区或互联网上的各种交互数据,以揭示其中隐藏的模式、关系和信息。这些社区可以是社交媒体平台、在线论坛、博客、微博等,人们在这些平台上进行交流…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
