【LeetCode】31. 下一个排列
1 问题
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
2 答案
这题直接不会,字典序如何排列?
官方解,从后向前迭代数组
class Solution:def nextPermutation(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""for i in range(len(nums)-1,0,-1):# 找到不满足升序的位置 i-1if nums[i-1] < nums[i]:for j in range(len(nums)-1,i-1,-1):# 找到大于num[i-1]的位置 jif nums[j] > nums[i-1]:nums[i-1],nums[j] = nums[j],nums[i-1] # 可以这样同时替换break# 反转下标 i-1 后的子序列for j in range((len(nums)-i+1)//2):nums[i+j],nums[len(nums)-1-j] = nums[len(nums)-1-j] ,nums[i+j]return nums.reverse() # 如果当前已经是最大,则直接翻转成最小的return
相关文章:

【LeetCode】31. 下一个排列
1 问题 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地&a…...

支持语音与视频即时通讯项目杂记(一)
第一部分解释服务端的实现。 (服务端结构) 下面一个用于实现TCP服务器的代码,包括消息服务器(TcpMsgServer)和文件中转服务器(TcpFileServer)。 首先,TcpServer是TcpMsgServer和Tcp…...

文档:htm格式转txt
꧂ 两个地方都保存꧁ import os import codecs from bs4 import BeautifulSoupdef generate_output_filename(file_path, save_path):# 获取文件名(不包含扩展名)file_name os.path.splitext(os.path.basename(file_path))[0]# 构造保存路径和文件名ou…...

电子邮件地址注册过程详解
许多人可能对如何注册电子邮件地址感到困惑,本文将详细解析电子邮件地址的注册过程:确定邮箱厂商、创建邮箱账户、设置电子邮件地址。 1、确定要注册的邮箱厂商 首先我们需要确定要注册哪种类型的电子邮件服务。目前市场上有许多不同的电子邮件服务提供商…...
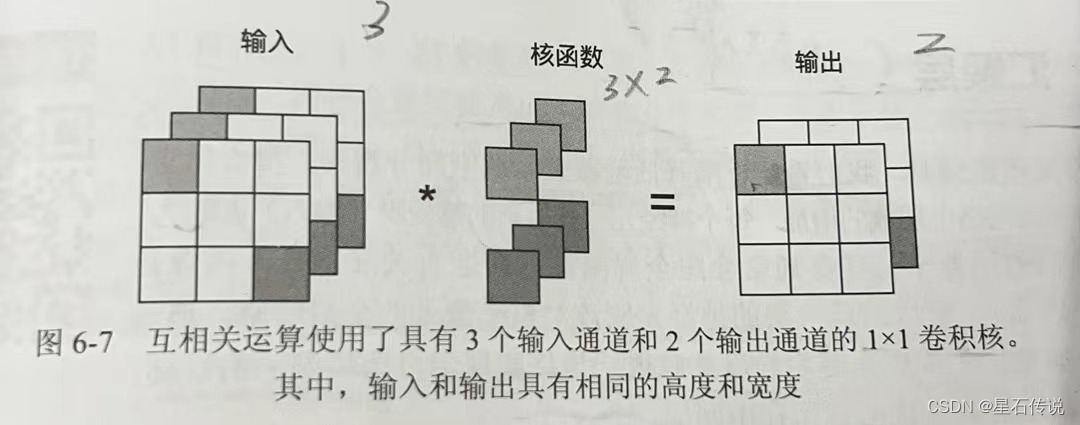
深度学习——卷积神经网络(CNN)基础二
深度学习——卷积神经网络(CNN)基础二 文章目录 前言三、填充和步幅3.1. 填充3.2. 步幅3.3. 小结 四、多输入多输出通道4.1. 多输入通道4.2. 多输出通道4.3. 11卷积层4.4. 小结 总结 前言 上文对卷积有了初步的认识,其实卷积操作就是通过卷积…...
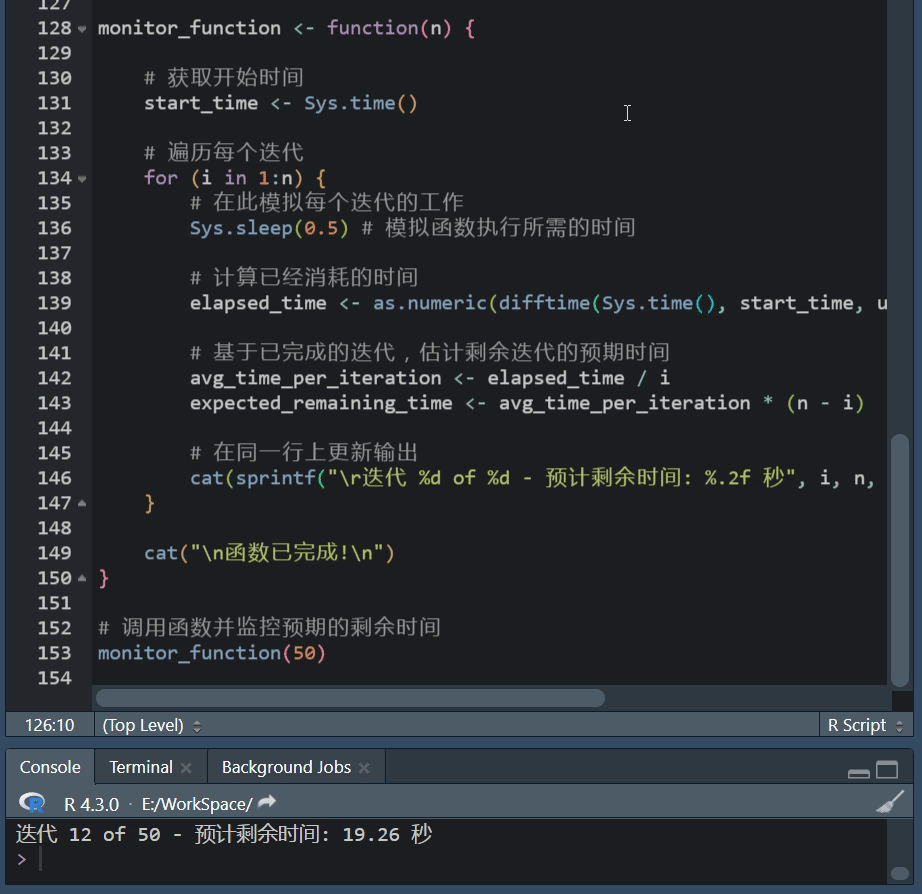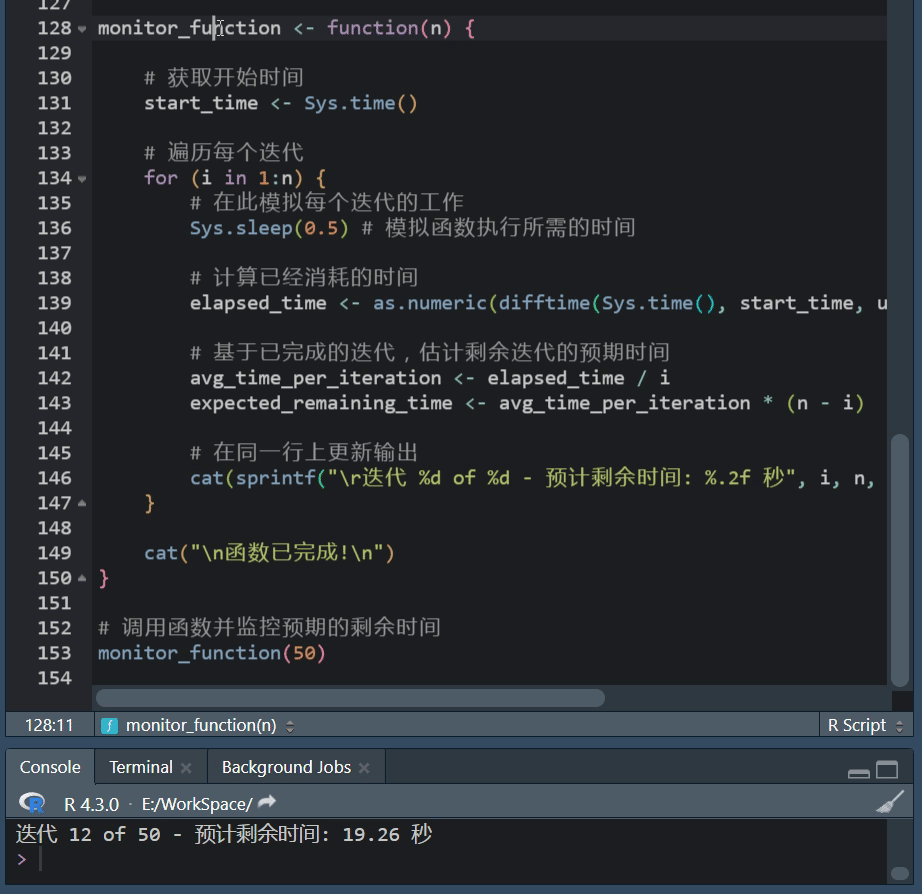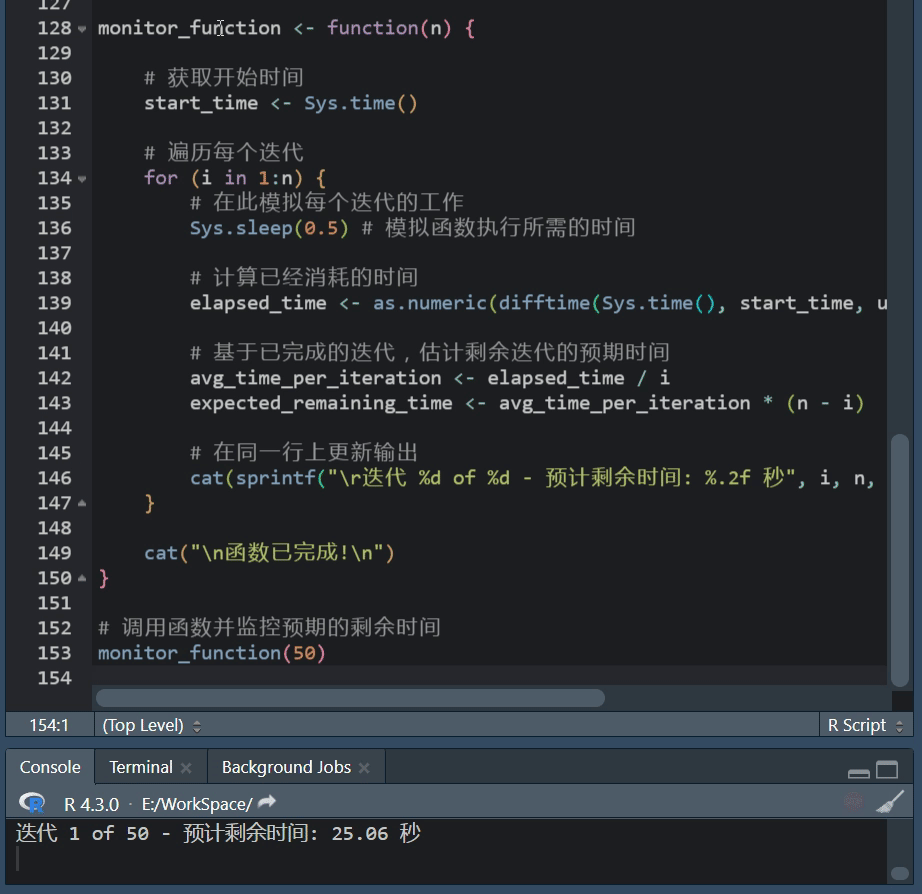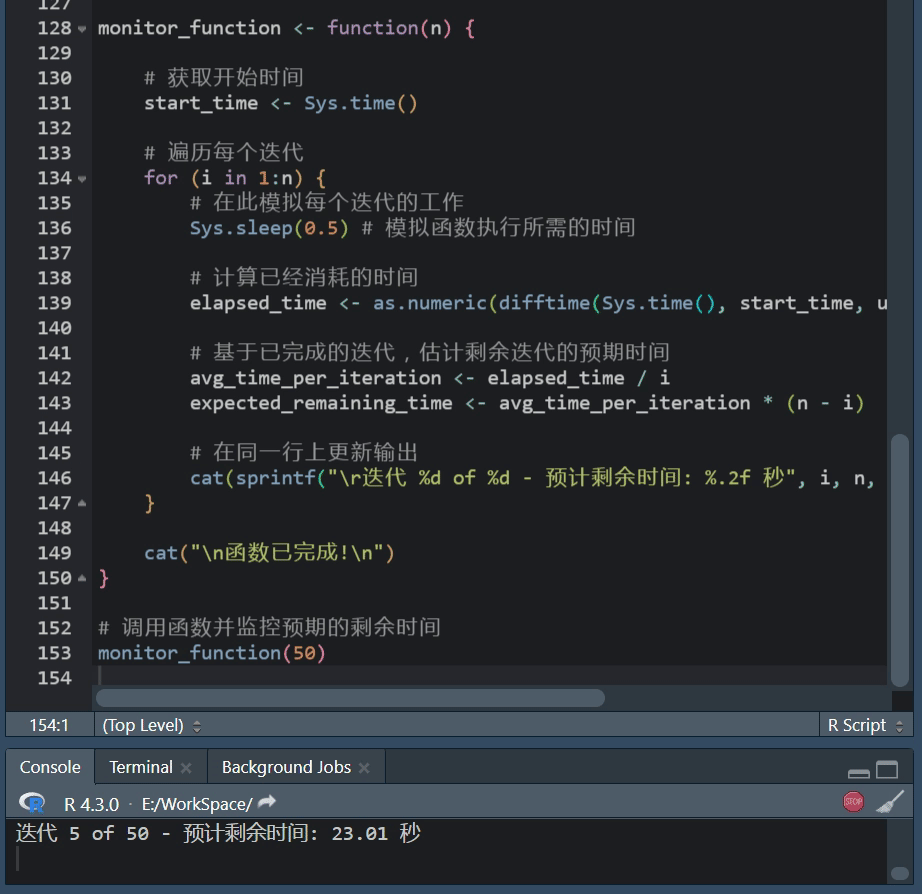
R语言进度条:txtProgressBar功能使用方法
R语言进度条使用攻略 在数据处理、建模或其他计算密集型任务中,我们常常会执行一些可能需要很长时间的操作。 在这些情况下,展示一个进度条可以帮助我们了解当前任务的进度,以及大约还需要多长时间来完成,R语言提供了几种简单且灵…...

Maven实战-声明周期和插件
Maven实战-声明周期和插件 Maven 设计了插件机制,每个构建步骤都可以绑定一个或者多个插件行为,而且 Maven 为大多数构建步骤编写 并绑定了默认插件。例如,针对编译的插件有 maven-compiler-plugin,针对测试的插件有 maven-sure…...
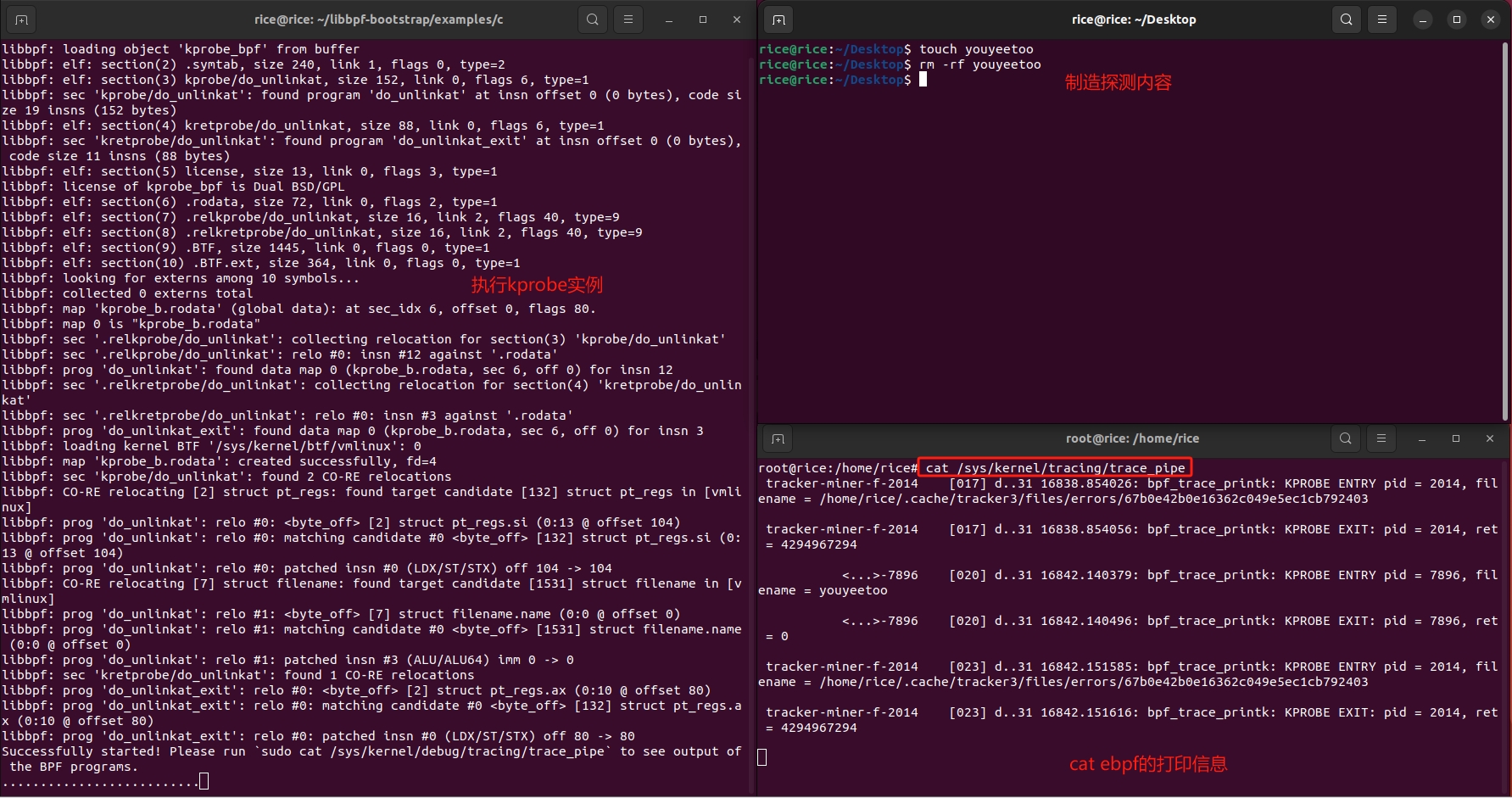
ebpf的快速开发工具--libbpf-bootstrap
基于ubuntu22.04-深入浅出 eBPF 基于ebpf的性能工具-bpftrace 基于ebpf的性能工具-bpftrace脚本语法 基于ebpf的性能工具-bpftrace实战(内存泄漏) 什么是libbpf-bootstrap libbpf-bootstrap是一个开源项目,旨在帮助开发者快速启动和开发使用eBPF(Extended Berk…...

万界星空科技/生产制造执行MES系统/开源MES/免费MES
开源系统概述: 万界星空科技免费MES、开源MES、商业开源MES、市面上最好的开源MES、MES源代码、免费MES、免费智能制造系统、免费排产系统、免费排班系统、免费质检系统、免费生产计划系统、免费数字化大屏。 万界星空开源MES制造执行系统的Java开源版本。开源mes…...

螺纹快速接头在卫浴行业中的应用提高产量降低生产成本
螺纹快速接头在卫浴行业主要用于上下水测试和密封性测试,可以快速密封连接待测产品和水管。取代之前的工人手拧编织管六角螺母的方式,方便快捷,密封性好,产品测试更稳定。 卫浴行业产品必须具备很好的密封性,防止在实际…...
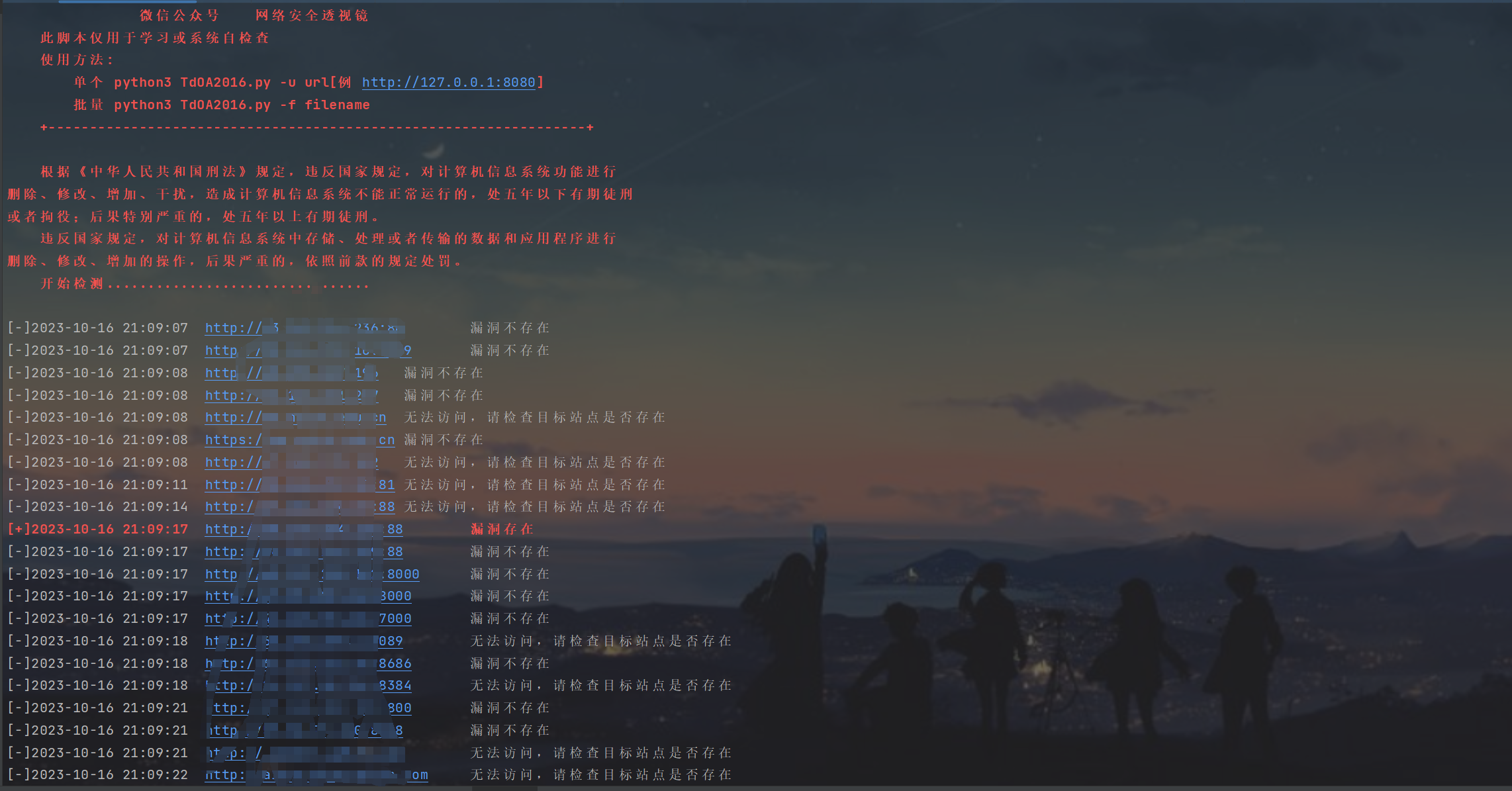
通达OA 2016网络智能办公系统 handle.php SQL注入漏洞
一、漏洞描述 北京通达信科科技有限公司通达OA2016网络智能办公系统 handle.php 存在sql注入漏洞,攻击者可利用此漏洞获取数据库管理员权限,查询数据、获取系统信息,威胁企业单位数据安全。 二、网络空间搜索引擎查询 fofa查询 app"T…...

parameter的各种用法以及localparam的用法
parameter的各种用法以及localparam的用法 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 一、这种写法放在v文件或者是用来调用其他的ram文件都是正确的。 module para_local();parameter a 10; // 第一种用法 parameter a 4d10; // 第二种用法 para…...

网络社区挖掘-图论部分的基本知识笔记
1 网络社区挖掘定义 网络社区挖掘是指利用数据挖掘技术和机器学习算法,分析社交网络、在线社区或互联网上的各种交互数据,以揭示其中隐藏的模式、关系和信息。这些社区可以是社交媒体平台、在线论坛、博客、微博等,人们在这些平台上进行交流…...

Vue Router - 路由的使用、两种切换方式、两种传参方式、嵌套方式
目录 一、Vue Router 1.1、下载 1.2、基本使用 a)引入 vue-router.js(注意:要在 Vue.js 之后引入). b)创建好路由规则 c)注册到 Vue 实例中 d)展示路由组件 1.3、切换路由的两种方式 1.…...

mysql为什么会选错索引,以及优化器是如何选择索引的
一:概念 在 索引建立之后,一条语句可能会命中多个索引,这时,索引的选择,就会交由 优化器 来选择合适的索引。 优化器选择索引的目的,是找到一个最优的执行方案,并用最小的代价去执行语句。 二…...
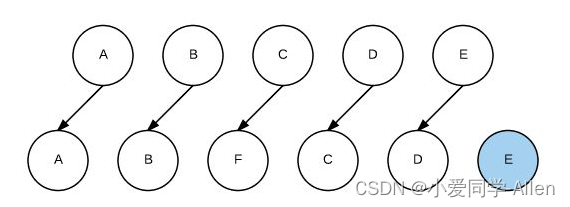
vue基础知识十七:你知道vue中key的原理吗?说说你对它的理解
一、Key是什么 开始之前,我们先还原两个实际工作场景 1.当我们在使用v-for时,需要给单元加上key <ul><li v-for"item in items" :key"item.id">...</li> </ul>2.用new Date()生成的时间戳作为key&#x…...
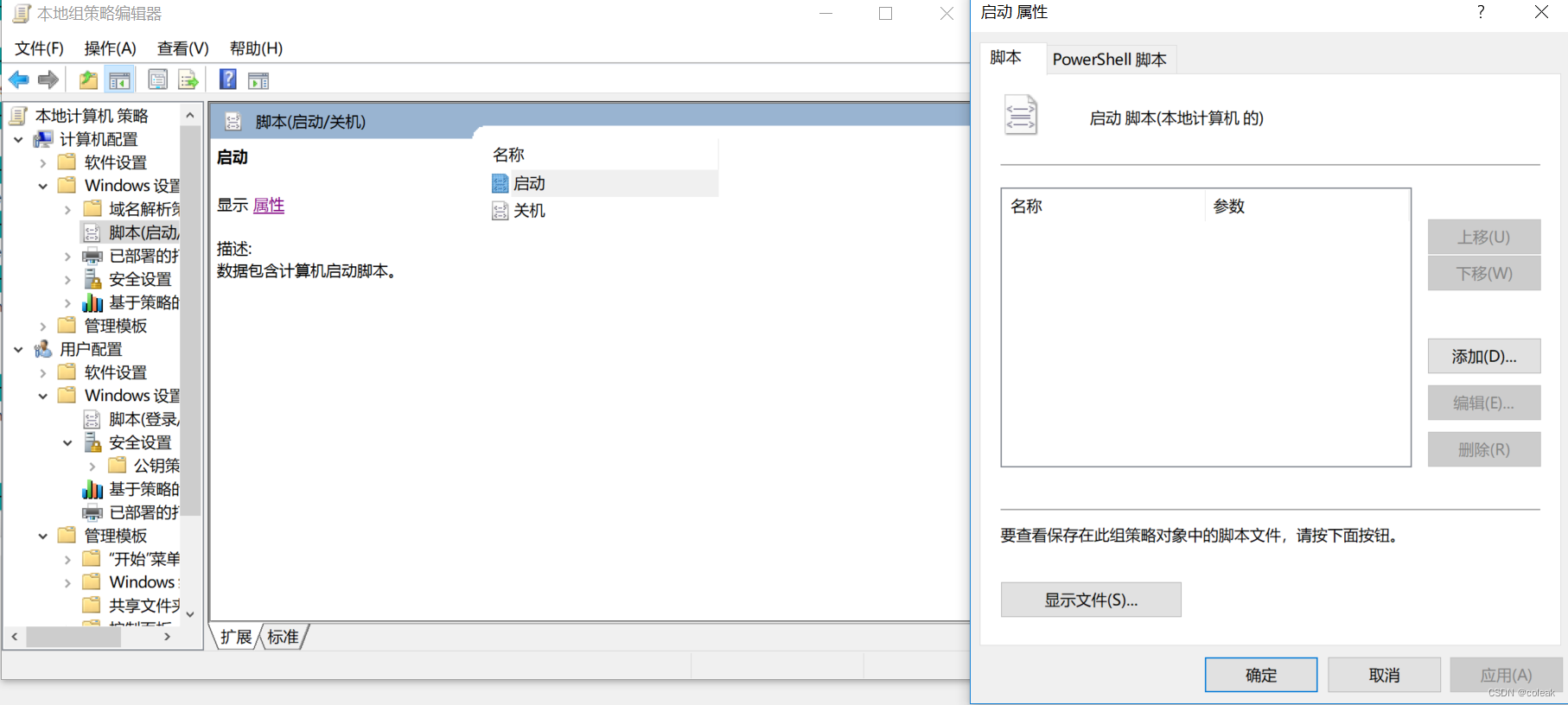
攻防演练蓝队|Windows应急响应入侵排查
文章目录 日志分析web日志windows系统日志 文件排查进程排查新增、隐藏账号排查启动项/服务/计划任务排查工具 日志分析 web日志 dirpro扫描目录,sqlmap扫描dvwa Python dirpro -u http://192.168.52.129 -b sqlmap -u "http://192.168.52.129/dvwa/vulnera…...

uniapp 小程序实现图片宽度100%、高度自适应的效果
因为image组件默认是有宽度跟高度的,所以这个高度不怎么好写 通过load事件来控制图片的高度 话不多说,直接上代码, <image class"img" src"/static/image.png" :style"{ height: imgHeight px }"mode&q…...

05. NXP官方SDK使用实验
05. NXP官方SDK使用实验 官方SDK移植 官方SDK移植 新建cc.h文件 SDK包里面会用到很多数据类型,所以需要在该文件中定义一些常用的数据类型 #pragma once #define __I volatile #define __O volatile #define __IO volatiletypedef sig…...

Python- JSON使用初探
JSON 在JSON格式中,{} 和 [] 是两种主要的数据结构,分别表示对象(或称为字典、哈希、map)和数组(或称为列表、序列)。 {} - 对象 在JSON中,对象是一组"key": value对的集合。这些键必…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
