TARJAN复习 求强连通分量、割点、桥
TARJAN复习 求强连通分量、割点、桥
文章目录
- TARJAN复习 求强连通分量、割点、桥
- 强连通分量
- 缩点
- 桥
- 割点
感觉之前写的不好,
强连通分量
“有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
----百度
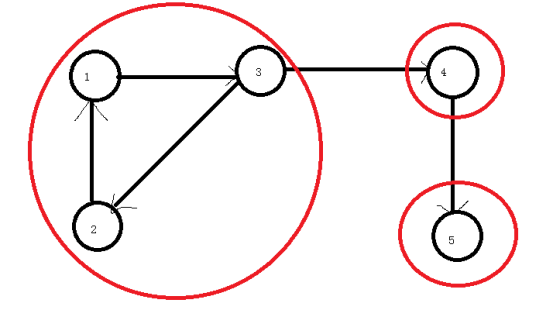
像上面的这个图就有三个强连通分量
1-2-3、4、5
设 d f n i dfn_i dfni 记录到达点 i i i 的时间戳
设 l o w i low_i lowi 表示 i i i 能到达的所有点的时间戳
如果 l o w i = = d f n i low_i == dfn_i lowi==dfni 就意味着 i i i 和 i i i 下面的点能够组成一个强连通分量,因为 i i i 下面已经没有边可以往 i i i 祖先方向上走了
实现的时候就用一个栈维护一下那个顺序就好了
缩点
P3387 【模板】缩点 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
看一下这个题
对于一个强连通分量来说
我们可以把它缩成一个点,并把这个点的权值设成这个强连通分量里面所有点的权值和。
然后再做 d p dp dp 就好了
#include<bits/stdc++.h>
#define LL long long
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
stack<int> stk;
queue<int> que;
const int N = 1e4 + 5 , M = 1e5 + 5;
LL ans , f[N] , w[N];
int hd[N] , hd2[N] , num , cnt2 , cnt , p[N] , dfn[N] , low[N] , a[N] , n , ru[N] , m , b[N] , num1;
struct E {int nt , to , fr;
}e[M << 1];
struct EE {int nt , to;
}e2[M << 1];
int read () {int val = 0 , fu = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') fu = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {val = val * 10 + (ch - '0');ch = getchar ();}return val * fu;
}
void add (int x , int y) {e[++cnt].to = y , e[cnt].nt = hd[x] , e[cnt].fr = x , hd[x] =cnt;
}
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;stk.push(x);int y;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (!dfn[y]) {dfs (y , x);low[x] = min (low[x] , low[y]);}else if (!p[y])low[x] = min (low[x] , dfn[y]);}if (low[x] == dfn[x]) {y = 0;num1 ++;while (y != x && !stk.empty()) {y = stk.top();stk.pop();p[y] = num1;w[num1] += a[y];}f[num1] = w[num1]; }
}
void add2 (int x , int y) { e2[++cnt2].to = y , e2[cnt2].nt = hd2[x] , hd2[x] = cnt2; }
void build () {int fa1 , fa2 , x , y;fu(i , 1 , cnt) {x = p[e[i].fr] , y = p[e[i].to];if (x == y) continue;add2 (x , y);ru[y] ++;}
}
void tuo () {fu(i , 1 , num1)if (!ru[i])que.push(i);int x , y;while (!que.empty()) {x = que.front();que.pop();for (int i = hd2[x] ; i ; i = e2[i].nt) {y = e2[i].to;ru[y] --;if (!ru[y])que.push(y);f[y] = max (f[y] , f[x] + w[y]);}}
}
int main () {int u , v;n = read () , m = read ();fu(i , 1 , n) a[i] = read ();fu(i , 1 , m) {u = read () , v = read ();add (u , v);}fu(i , 1 , n)if (!dfn[i])dfs (i , 0);build ();tuo ();fu(i , 1 , num)ans = max (ans , f[i]);printf ("%lld" , ans);return 0;
}
桥
在一个图中,如果存在一条边,把它删掉,使得整个图被分出来两个互相不连通的图,那么这条边就是桥
d f n dfn dfn 跟求强连通分量的一样
l o w i low_i lowi 表示 i i i 能够到达的最先被访问过的点**(不包括 i i i 的父亲)**
设 u , v u , v u,v , v v v 是 u u u 的儿子。
如果 l o w v > d f n u low_v > dfn_u lowv>dfnu 就意味着 v v v 不能到达 u u u 之前的点了,除非经过 u → v u\to v u→v 这条边,所以这条边就是桥
P1656 炸铁路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 155 , M = 5005;
int n , m , hd[N] , cnt = 1 , dfn[N] , low[N] , num , ans1;
struct E {int to , nt;
} e[M << 1];
struct ANS {int u , v;
} ans[M];
bool cmp (ANS x , ANS y) { return x.u != y.u ? x.u < y.u : x.v < y.v; }
void add (int x , int y) { e[++cnt].to = y , e[cnt].nt = hd[x] , hd[x] = cnt; }
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;int y;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (y == fa) continue;if (!dfn[y]) {dfs (y , x);if (dfn[x] < low[y]) {ans[++ans1].u = min (x , y);ans[ans1].v = max (x , y);}low[x] = min (low[x] , low[y]);}elselow[x] = min (low[x] , dfn[y]);}
}
int main () {int u , v;scanf ("%d%d" , &n , &m);fu (i , 1 , m) {scanf ("%d%d" , &u , &v);add (u , v) , add (v , u);}fu (i , 1 , n) {if (!dfn[i]) dfs (i , 0);}sort (ans + 1 , ans + ans1 + 1 , cmp);fu (i , 1 , ans1) printf ("%d %d\n" , ans[i].u , ans[i].v);return 0;
}
割点
在一个图中,如果能够删掉一个点和连接这个点的所有边,使得这个图分成两个不相连的连通块,那么这个点就是割点
跟桥差不多。
因为当你找到一条桥连接 u , v u , v u,v ,且 u u u 是 v v v 的父亲时, u u u 一定是割点,因为 v v v 连不出去了
还有一种情况就是 u u u 是根,且 u u u 有超过一个不同的子树,那么 u u u 也是割点。
P3388 【模板】割点(割顶) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 2e4 + 5 , M = 2e5 + 5;
int n , m , cnt , hd[N] , dfn[N] , low[N] , num , flg[N] , ans;
struct E {int to , nt;
} e[M << 1];
void add (int x , int y) { e[++cnt].to = y , e[cnt].nt = hd[x] , hd[x] = cnt; }
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;int y , sz = 0;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (!dfn[y]) {dfs (y , x);if (dfn[x] <= low[y] && fa)flg[x] = 1;low[x] = min (low[x] , low[y]);sz ++;}elselow[x] = min (low[x] , dfn[y]);}if (!fa && sz >= 2)flg[x] = 1;if (flg[x]) ans ++;
}
int main () {int u , v;scanf ("%d%d" , &n , &m);fu (i , 1 , m) {scanf ("%d%d" , &u , &v);add (u , v) , add (v , u);}fu (i , 1 , n) {if (!dfn[i]) dfs (i , 0);}printf ("%d\n" , ans);fu (i , 1 , n)if (flg[i])printf ("%d " , i);return 0;
}
相关文章:

TARJAN复习 求强连通分量、割点、桥
TARJAN复习 求强连通分量、割点、桥 文章目录 TARJAN复习 求强连通分量、割点、桥强连通分量缩点桥割点 感觉之前写的不好, 再水一篇博客 强连通分量 “有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有…...

python实现批量数据库数据插入
import pandas as pd import pymysql # 连接 MySQL 数据库 conn pymysql.connect( hostlocalhost, useryour_username, passwordyour_password, databaseyour_database_name, charsetutf8mb4, ) # 读取已有数据 existing_data pd.read_csv("86w全…...

python安装,并搞定环境配置和虚拟环境
鄙人使用Python来进行项目的开发,一般都是通过Anaconda来完成的。Anaconda不但封装了Python,还包含了创建虚拟环境的工具。 anaconda安装 安装anaconda,可以搜索清华镜像源,然后搜索anaconda,点击进入,然…...
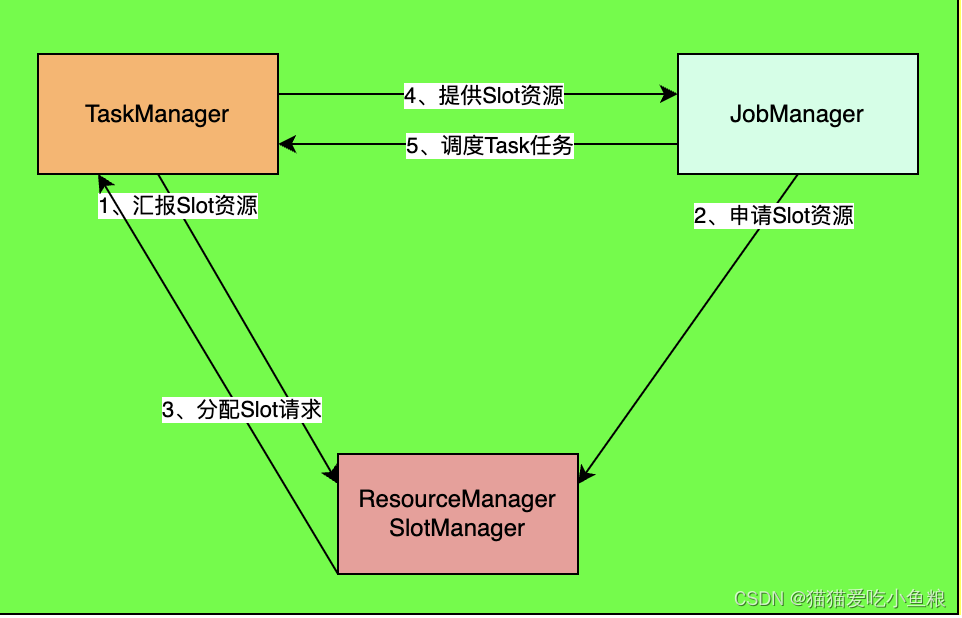
Flink 的集群资源管理
集群资源管理 一、ResourceManager 概述 1、ResourceManager 作为统一的集群资源管理器,用于管理整个集群的计算资源,包括 CPU资源、内存资源等。 2、ResourceManager 负责向集群资源管理器申请容器资源启动TaskManager实例,并对TaskManag…...

STM32学习笔记
前言 今天开始学习STM32,公司封闭git网络,所以选择CSDN来同步学习进度,方便公司和家里都能更新学习笔记。 参考学习资料 江科大STM32教学视频: 江科大自动协STM32视频_哔哩哔哩_bilibili...
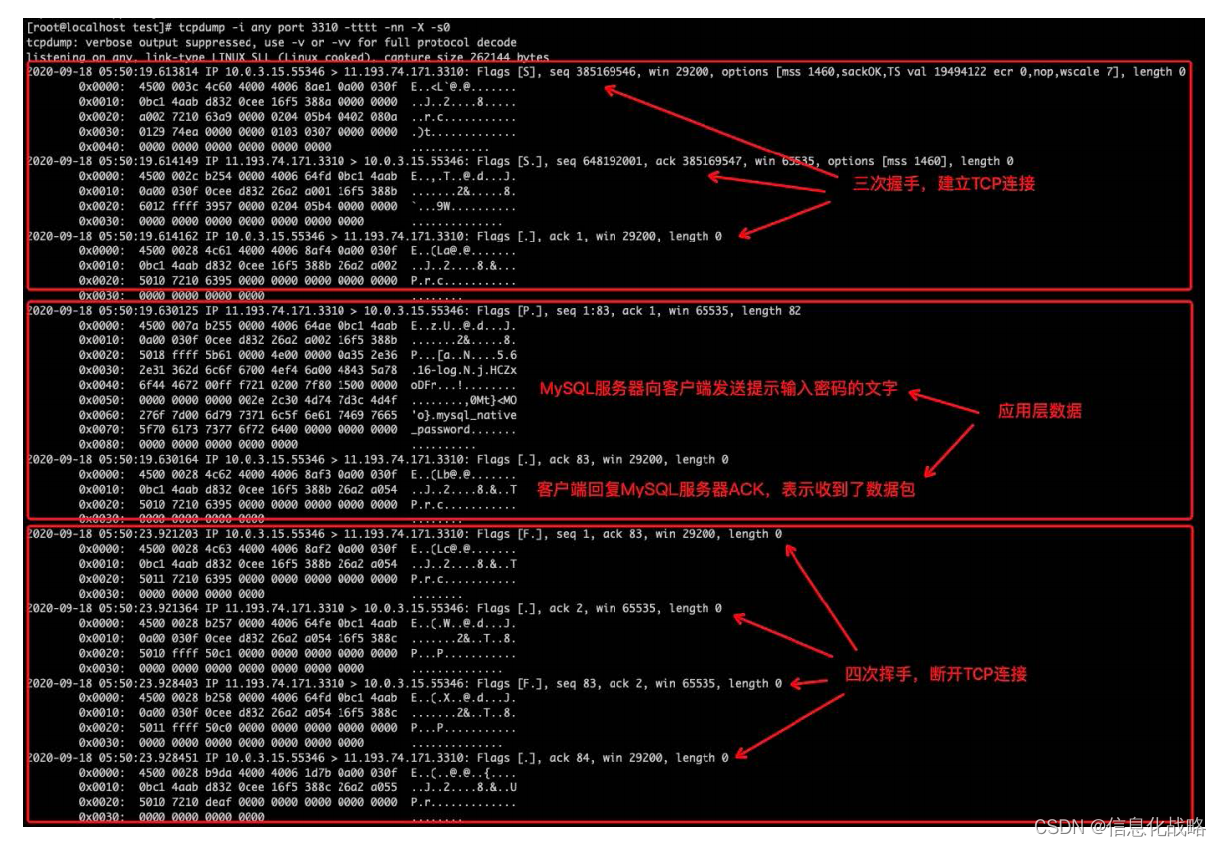
Java应用性能问题诊断技巧
作者:张彦东 参考:https://developer.aliyun.com/ebook/450?spma2c6h.20345107.ebook-index.28.6eb21f54J7SUYc 文章目录 (一)内存1.内存2.内存-JMX3.内存-Jmap4.内存-结合代码确认问题 (二)CPU1.CPU-JMX或…...

监控系列(六)prometheus监控DMHS操作步骤
一、监控的操作逻辑 给操作系统安装expect命令expect脚本执行dmhs_console脚本执行 cpt / exec 命令用脚本进行过滤字符串过滤dm_export读取脚本与当前日期作比较,然后返回差值 二、安装步骤 1. linux中Expect工具的安装及使用方法 https://blog.csdn.net/wangta…...

SLAM从入门到精通(dwa速度规划算法)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 要说搜路算法,这个大家都比较好理解。毕竟从一个地点走到另外一个地点,这个都是直觉上可以感受到的事情。但是这条道路上机…...
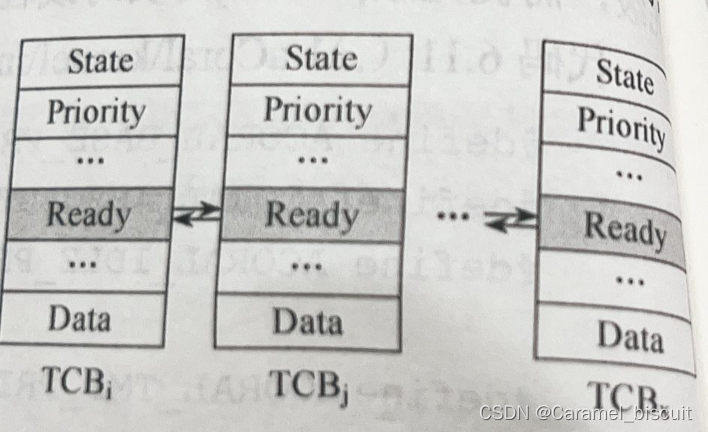
嵌入式实时操作系统的设计与开发(aCoral线程学习)
真正的RTOS,基本上没有做到进程,只是停留在多线程,因为多进程要解决很多问题,且需要硬件支持,这样就使得系统复杂了,从而就可能影响系统实时性。 线程之间是共享地址的,也就是说当前线程的地址…...
JAVA基础(JAVA SE)学习笔记(二)变量与运算符
前言 1. 学习视频: 尚硅谷Java零基础全套视频教程(宋红康2023版,java入门自学必备)_哔哩哔哩_bilibili 2023最新Java学习路线 - 哔哩哔哩 正文 第一阶段:Java基本语法 1. Java 语言概述 JAVA基础(JAVA SE)学习…...

chatgpt 接口 和 jupyter版本安装
一 接口代码 有时间继续测试 import openai # 填入你的api_key openai.api_key ""models openai.Model.list()# 定义API参数 params {role: "user", "content": }# 定义循环 while True:# 获取用户输入user_input input("请输入您的消…...

ubuntu20.04 nerf开山之作
源码 GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results. 代码的相关解读 NeRF代码解读-相机参数与坐标系变换 - 知乎 原文题目:NeRF: Representing Scenes as Neural Radiance Field…...

Java 中实现单例模式
单例模式 单例模式,就是一个类在任何情况下绝对只有一个实例,并且提供一个全局访问点来获取该实例。 要实现单例,至少需要满足两个点: 私有化构造方法,防止被外部实例化造成多实例问题 提供一个静态方位作为全局访问点…...
标签页的使用
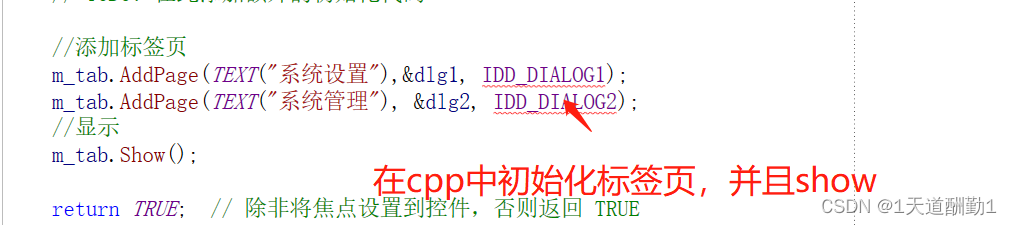
目录 1、引用TabSheet.h和TabSheet.cpp文件: 2、主窗口添加标签页: (1)、标签页的创建和属性更改 (2)、添加俩个标签页的类 (3)、主窗口添加成员变量 (4)…...
新一代开源语音库CoQui TTS冲到了GitHub 20.5k Star
Coqui TTS 项目介绍 Coqui 文本转语音(Text-to-Speech,TTS)是新一代基于深度学习的低资源零样本文本转语音模型,具有合成多种语言语音的能力。该模型能够利用共同学习技术,从各语言的训练资料集转换知识,来…...
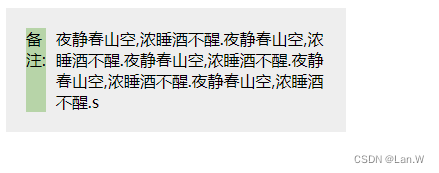
CSS 效果:多列文字,第一行对齐,flex方式元素被挤压
如图效果:2列,第一列只有一行,第二列多行。要求第一行对齐 实现:使用flex 如果不配置flex-shrink的话,第一列会被挤压 给第一列:备注配置压缩属性: flex-shrink:0。 <!DOCTYPE…...
优维低代码实践:片段
优维低代码技术专栏,是一个全新的、技术为主的专栏,由优维技术委员会成员执笔,基于优维7年低代码技术研发及运维成果,主要介绍低代码相关的技术原理及架构逻辑,目的是给广大运维人提供一个技术交流与学习的平台。 优维…...

【计算机网络】第一章、计算机网络体系结构
1.1计算机网络的组成与分类 1.计算机网络的组成 从不同的角度来看内容从组成上看硬件、软件、协议从工作方式上岸边缘部分、核心部分从功能上看通信子网、资源子网 2.计算机网络的分类 角度内容分布范围广域网、城域网、局域网、个域网传输技术广播式网络、点对点网络拓扑结…...

vr火灾逃生安全科普软件开展消防突击教育安全有效
VR火灾逃生自救虚拟体验是一种利用虚拟现实技术来模拟火灾逃生自救场景的教育工具。以下是这个体验的几个优点:VR消防安全体验馆的出现,为城市的安全教育开辟了新的途径。这种创新的体验方式,能够让市民在模拟的火灾场景中学习并掌握消防安全…...
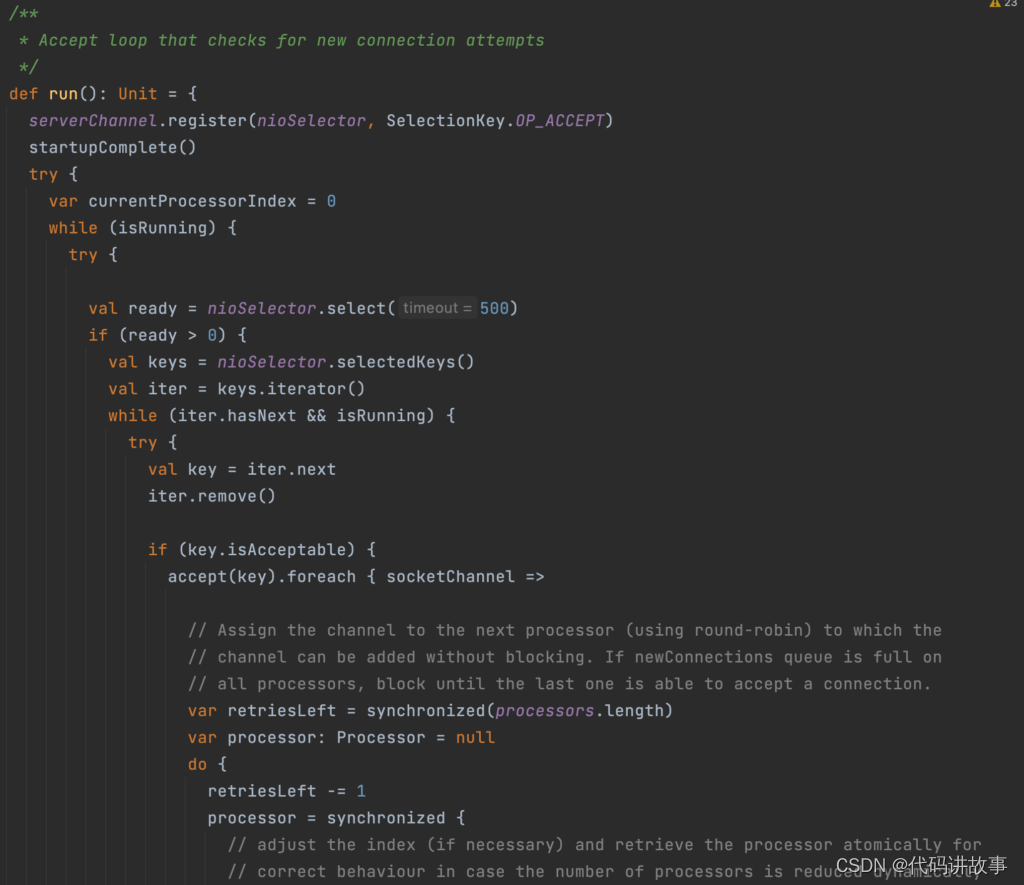
Kafka SASL认证授权(五)ACL源码解析
Kafka SASL认证授权(五)ACL源码解析。 官网地址:https://kafka.apache.org/ 一、ACL检查流程解析 一起看一下kafka server的启动与监听流程: Kafka -> KafkaServer -> SocketServer、KafkaRequestHandler 其中KafkaServer做相关的初始化,包括SocketServer 与 han…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
