基于Frenet优化轨迹的⾃动驾驶动作规划⽅法
动作规划(Motion Control)在⾃动驾驶汽⻋规划模块的最底层,它负责根据当前配置和⽬标配置⽣成⼀序列的动作,本⽂介绍⼀种基于Frenet坐标系的优化轨迹动作规划⽅法,该⽅法在⾼速情况下的ACC辅助驾驶和⽆⼈驾驶都具有较强的实⽤性,是⽬前普遍采⽤的⼀种动作规划算法。
基于Frenet坐标系的动作规划⽅法是由宝⻢的Moritz Werling提出的,为了简便,我们在后⽂中也会使⽤Werling⽅法简称。
在讨论基于Frenet坐标系的动作规划⽅法之前,⾸先定义什么是最优的动作序列:对于横向控制⽽⾔,假定由于⻋辆因为之前躲避障碍物或者变道或者其他制动原因⽽偏离了期望的⻋道线,那么此时最优的动作序列(或者说轨迹)是在⻋辆制动能⼒的限制下,相对最安全,舒适,简单和⾼效的轨迹。
同样的,纵向的最优轨迹也可以这么定义:如果⻋辆此时过快,或者太接近前⽅⻋辆,那么就必须做减速,具体什么是“舒适⽽⼜简单的”减速呢?
我们可以使⽤ Jerk 这个物理量来描述,Jerk即加速度的变化率,也即加加速度,通常来说,过⾼的加加速度会引起乘坐者的不适,所以,从乘坐舒适性⽽⾔,应当优化Jerk这个量,同时,引⼊轨迹的制动周期 T , 即⼀个制动的操作时间:

1
为什么使⽤Frenet坐标系
在Frenet坐标系中,使⽤道路的中⼼线作为参考线,使⽤参考线的切线向量t和法线向量n建⽴⼀个坐标系,如下图的右图所⽰,这个坐标系即为Frenet坐标系,它以⻋辆⾃⾝为原点,坐标轴相互垂直,分为s⽅向(即沿着参考线的⽅向,通常被称为纵向,Longitudinal)和d⽅向(即参考线当前的法向,被称为横向,Lateral)
相⽐于笛卡尔坐标系(下图的左图),Frenet坐标系明显地简化了问题,因为在公路⾏驶中,我们总是能够简单的找到道路的参考线(即道路的中⼼线),那么基于参考线的位置的表⽰就可以简单的使⽤纵向距离(即沿着道路⽅向的距离)和横向距离(即偏离参考线的距离)来描述,同样的,两个⽅向的速度

的计算也相对简单。

那么现在动作规划问题中的配置空间就⼀共有三个维度:

是规划出来的每⼀个动作的时间点,轨迹和路径的本质区别就是轨迹考虑了时间这⼀维度。Werling的动作规划⽅法⼀个很关键的理念就是将动作规划这⼀⾼维度的优化问题分割成横向和纵向两个⽅向上的彼此独⽴的优化问题,具体来看下⾯的图:

假设⾏为规划层要求当前⻋辆在
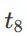
越过虚线完成⼀次变道,即⻋辆在横向上需要完成⼀个
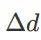
以及纵向上完成⼀个 的移动,则可以将s和d分别表⽰为关于t的函数:

(上图右图),那么d,s关于时间t的最优轨迹应该选择哪⼀条呢?
通过这种转换原来的动作规划问题被分割成了两个独立的优化问题,对于横向和纵向的轨迹优化,我们选取损失函数C,将使得C最⼩的轨迹作为最终规划的动作序列。而Werling方法中损失函数的定义,则与我们前⾯提到的加加速度 Jerk 相关。
2
Jerk最⼩化和5次轨迹多项式求解
由于我们将轨迹优化问题分割成了s和d两个⽅向,所以Jerk最⼩化可以分别从横向和纵向进⾏,令p为我们考量的配置(即s或d),加加速度
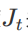
关于配置p在时间段
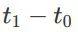
内累计的Jerk的表达式为:
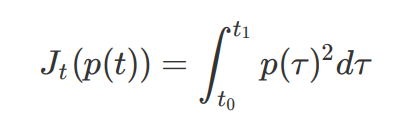
现在我们的任务是找出能够使得

,Takahashi的⽂章motion control for AGV in positioning中已经证明,任何Jerk最优化问题中的解都可以使⽤⼀个5次多项式来表⽰:
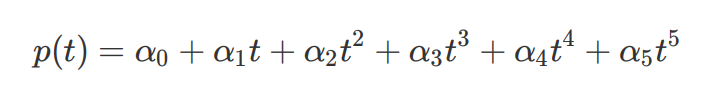
要解这个⽅程组需要⼀些初始配置和⽬标配置,以横向路径规划为例,初始配置为

,即
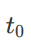
时刻⻋辆的横向偏移,横向速度和横向加速度为

,即可得⽅程组:
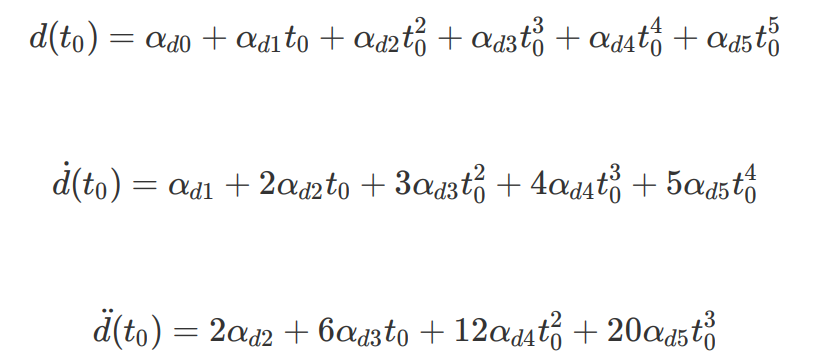
为了区分横向和纵向,我们使⽤

来分别表⽰d和s⽅向的多项式系数,同理,根据横向的⽬标配置
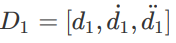
可得⽅程组:
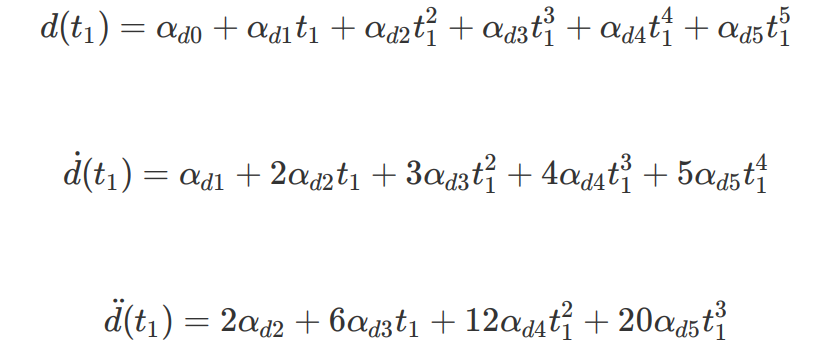

该⽅程的解可以通过Python的Numpy中的 np.linalg.solve简单求得。⾄此,我们在给定任意的初始配置

,⽬标配置
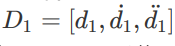
以及制动时间T的情况下,可以求的对应的d⽅向关于时间t的五次多项式的系数,同理,可以使⽤相同的⽅法来求解纵向(即s⽅向)的五次多项式系数。那么问题来了,我们如何去确定最优的轨迹呢?
Werling⽅法的思路是通过⼀组⽬标配置来求得轨迹的备选集合,然后在备选集合中基于Jerk最⼩化的原则选择最优轨迹 ,我们仍然以d⽅向的优化轨迹为例讲解:
我们可以取如下⽬标配置集合来计算出⼀组备选的多项式集合:
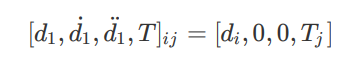
对于优化问题⽽⾔,我们实际上希望⻋辆最终沿着参考线(道路中⼼线)平⾏的⽅向⾏驶,所以我们令

,那么⽬标配置只涉及

两个变量的组合,⽽这两个变量在⽆⼈驾驶的应⽤场景中实际上是受限的,我们可以通过定义

来约束⽬标配置的取值范围,通过 和 来限制采样密度,从⽽在每⼀个制动周期获得⼀个有限的备选轨迹集合,如下图所⽰:
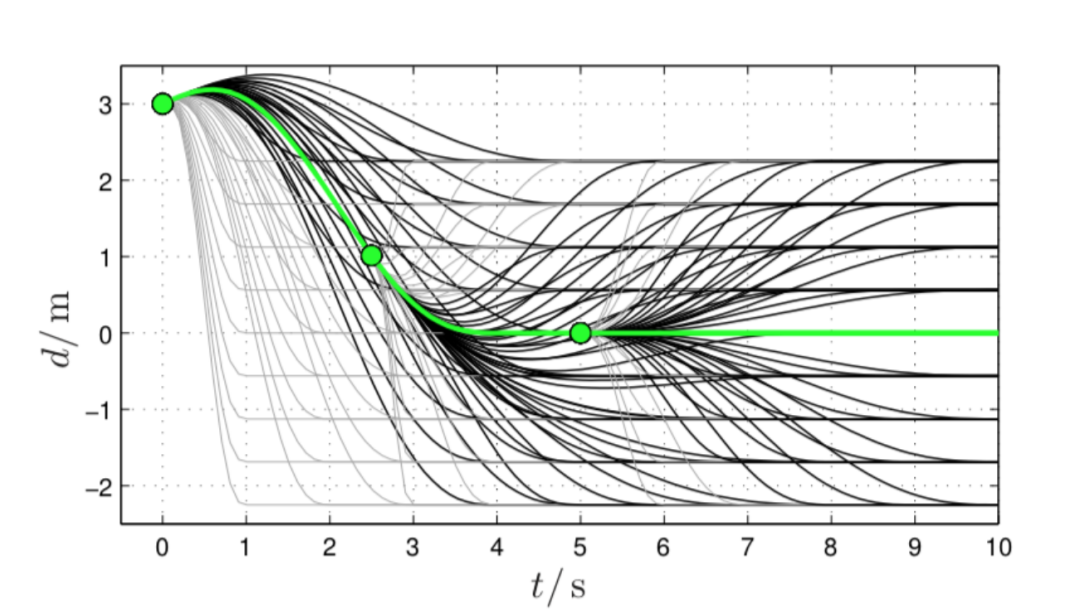
要在备选集合中选择最优轨迹(即上图中的绿⾊轨迹),我们需要设计损失函数,对于不同的场景,损失函数也不相同,以横向轨迹为例,在较⾼速度的情况下,损失函数为:
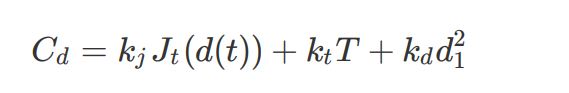
该损失函数包含三个惩罚项:

其中
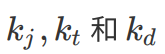
是这三个惩罚项的系数,它们的⽐值⼤⼩决定了我们的损失函数更加注重哪⼀个⽅⾯的优化,由此我们可以算出所有备选轨迹的损失,取损失最⼩的备选轨迹作为我们最终的横向轨迹。
值得注意的是,以上的损失函数仅适⽤于相对⾼速度的场景,在极端低速的情况下,⻋辆的制动能⼒是不完整的,我们不再将d表⽰为关于时间t的五次多项式,损失函数也会略有不同,但是这种基于有限采样轨迹,通过优化损失函数搜索最优轨迹的⽅法仍然是⼀样的,在此不再赘述。
讨论完横向的轨迹优化问题,我们再来看看纵向的轨迹优化,在不同的场景下纵向轨迹的优化的损失函数也各不相同,Werling⽅法中将纵向轨迹的优化场景⼤致分成如下三类:
跟⻋
汇流和停⻋
⻋速保持
在本⽂中我们详细了解⻋速保持场景下的纵向轨迹优化,在⾼速公路等应⽤场景中,⽬标配置中并不需要考虑⽬标位置(即 ),所以在该场景下,⽬标配置仍然是 ,⽬标配置变成了 ,损失函数为:
其中 是我们想要保持的纵向速度,第三个惩罚项的引⼊实际上是为了让⽬标配置中的纵向速度尽可能接近设定速度,该情景下的⽬标配置集为:

即优化过程中的可变参数为

,同样,也可以通过设置

来设置轨迹采样的密度,从⽽获得⼀个有限的纵向轨迹集合:

其中,绿线即为纵向最优轨迹。以上我们分别讨论了横向和纵向的最优轨迹搜索⽅法,在应⽤中,我们将两个⽅向的损失函数合并为⼀个,即:

这样,我们就可以通过最⼩化
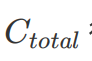
得到优化轨迹集合(我们不能得到“最优”的轨迹多项式参数,还可以得到“次优”,“次次优”轨迹等等)。
3
事故避免
(Collision Avoiding)
显然,上⾯的轨迹优化损失函数中并没有包含关于障碍物躲避的相关惩罚,并且我们的损失函数中也没有包含最⼤速度,最⼤加速度和最⼤曲率等制动限制,也就是说我们的优化轨迹集合并没有考虑障碍物规避和制动限制因素,不将障碍物避免加⼊到损失函数中的⼀个重要的原因在于碰撞惩罚项的引⼊将代⼊⼤量需要⼈⼯调整的参数(即权重),是的损失函数的设计变得复杂 ,Werling⽅法将这些因素的考量独⽴出来,在完成优化轨迹以后进⾏。
具体来说,我们会在完成所有备选轨迹的损失计算以后进⾏⼀次轨迹检查,过滤掉不符合制动限制的,可能碰撞障碍物的轨迹,检查内容包括:
s⽅向上的速度是否超过设定的最⼤限速
s⽅向的加速度是否超过设定的最⼤加速度
轨迹的曲率是否超过最⼤曲率
轨迹是否会引起碰撞(事故)
通常来说,障碍物规避⼜和⽬标⾏为预测等有关联,本⾝即使⼀个复杂的课题,⾼级⾃动驾驶系统通常具备对⽬标⾏为的预测能⼒,从⽽确定轨迹是否会发⽣事故。
在本节中,我们关注的重点是⾃动驾驶汽Ctotal =klat Cd +k C lonsC total⻋的动作规划,故后⾯的实例仅涉及静态障碍物的规避和动作规划。
4
基于Frenet优化轨迹的
⾃动驾驶汽⻋动作规划实例
由于planner的代码篇幅过⻓,本实例完整代码请⻅⽂末链接,在此仅讲解算法核⼼代码内容。和之前⼀样,我们仍然使⽤Python来实现该动作规划算法。⾸先,我们⽣成要追踪的参考线以及静态障碍物,参考线的⽣成只要使⽤了我们上⼀节提到的⽴⽅样条插值,代码如下:

⽣成如下参考路径以及障碍物:
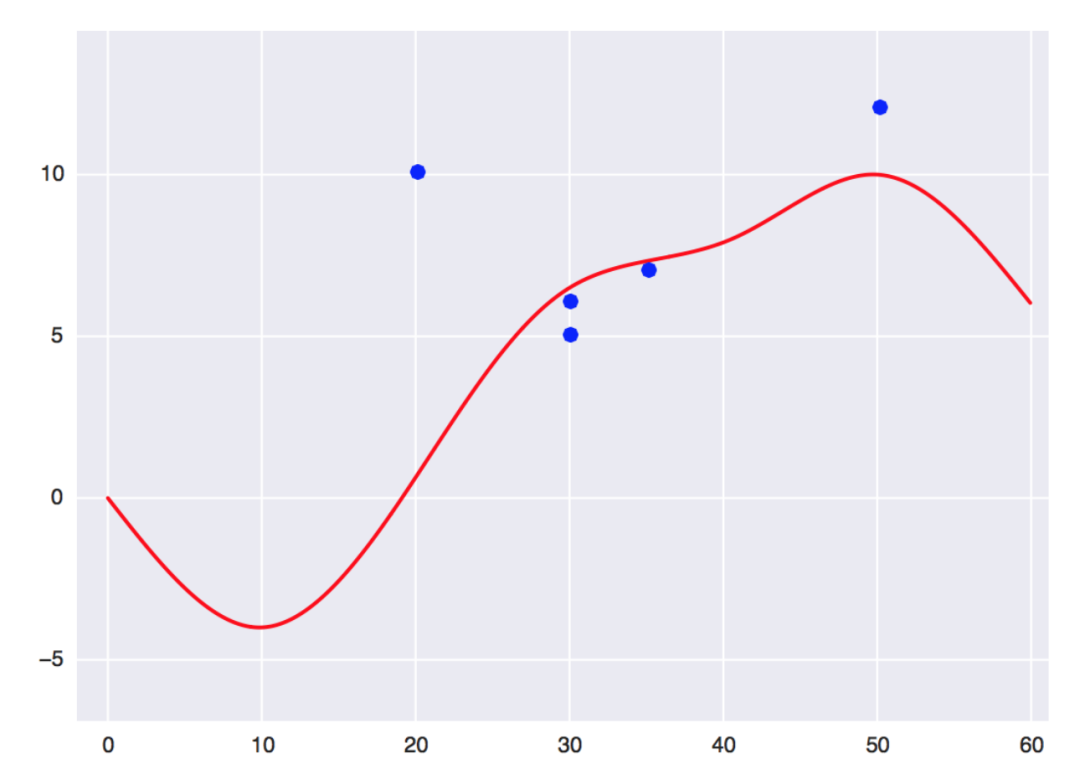
其中红线就是我们的全局路径,蓝点为障碍物。定义⼀些参数:

使⽤基于Frenet的优化轨迹⽅法⽣成⼀系列横向和纵向的轨迹,并且计算每条轨迹对应的损失:

其中,⼀个重要的类是五次多项式类,其定义如下:

这⾥的五次多项式的系数的求解过程和我们前⾯的理论讲解是⼀样的,只不过我们使⽤Numpy中的 np.linalg.solve(A, b)⽅法将矩阵解了出来。最后,我们来看⼀下障碍物规避是如何实现的:

由于我们将障碍物规避问题都简化为静态了,所以在这⾥我们只简单地计算了所有规划点到障碍物的距离,⼀句距离预计是否会发⽣碰撞,来看看完整的优化轨迹检查函数:

由此可以看出,最终的优化轨迹的选择并不单纯基于最⼩损失函数,轨迹检查还会过滤掉⼀些轨迹,所以使⽤基于Frenet的优化轨迹来做⾃动驾驶汽⻋的动作规划,通常能够找到有限集的最优解,当最优解⽆法通过检查是,⾃会采⽤“次优解”甚⾄更加“次优的”解。最后我们来看⼀下完整的动作规划效果:
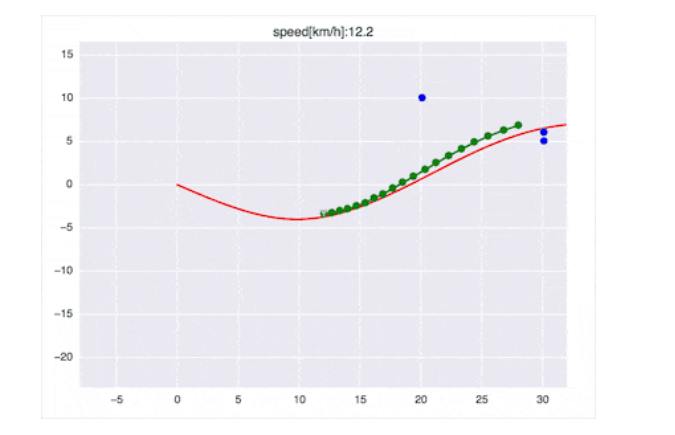
后台回复“21”领取完整代码~
相关文章:

基于Frenet优化轨迹的⾃动驾驶动作规划⽅法
动作规划(Motion Control)在⾃动驾驶汽⻋规划模块的最底层,它负责根据当前配置和⽬标配置⽣成⼀序列的动作,本⽂介绍⼀种基于Frenet坐标系的优化轨迹动作规划⽅法,该⽅法在⾼速情况下的ACC辅助驾驶和⽆⼈驾驶都具有较强…...
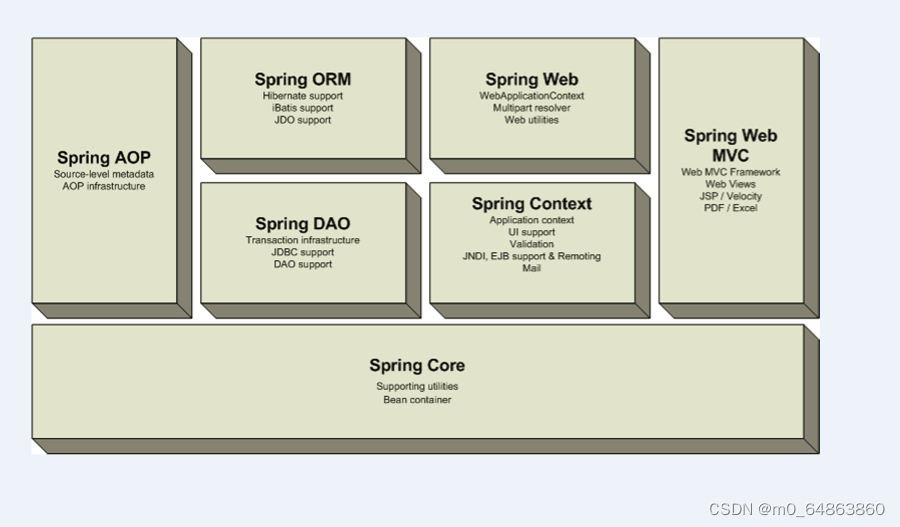
Spring(入门)
1. 什么是spring,它能够做什么?2. 什么是控制反转(或依赖注入)3. AOP的关键概念4. 示例 4.1 创建工程4.2 pom文件4.3 spring配置文件4.4 示例代码 4.4.1 示例14.4.2 示例2 (abstract,parent示例)4.4.3 使用有参数构造方法创建jav…...

2023-02-25力扣每日一题
链接: https://leetcode.cn/problems/minimum-swaps-to-make-strings-equal/ 题意: 给定字符串s1,s2,仅由x,y组成 每次可以在两边各挑一个字符交换 求让s1等于s2的最小步骤 解: 1000啊1000,双指针贪一下就过了 …...
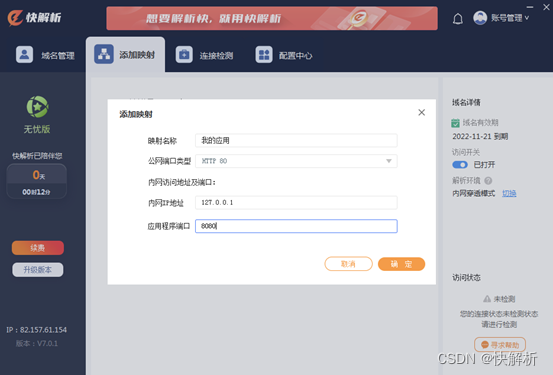
如何外网登录管理云通信短信网关平台?——快解析映射方案
云通信(Cloud Communications )是基于云计算商业模式应用的通信平台服务,简单易用,满足企业一键群发场景,支持多种语言SDK和API 接入。各个通信平台软件都集中在云端,且互通兼容,用户只要登录云通信平台,不…...

学习 Python 之 Pygame 开发魂斗罗(三)
学习 Python 之 Pygame 开发魂斗罗(三)继续编写魂斗罗1. 角色站立2. 角色移动3. 角色跳跃4. 角色下落继续编写魂斗罗 在上次的博客学习 Python 之 Pygame 开发魂斗罗(二)中,我们完成了角色的创建和更新,现…...

【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 分积木(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 吃火锅(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - RSA 加密算法(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 构成的正方形数量(2023.Q1) 【华为OD机试模拟…...

linux系统加exfat驱动
u盘假如是fat格式不支持大于4G文件,所以一般u盘用exfat格式,兼容性更好 有的老linux没支持exfat格式,那就自己装个驱动吧 sudo apt-get install exfat-fuse exfat-utils 有一台fedora27需要yum安装,国外源比较慢,改…...
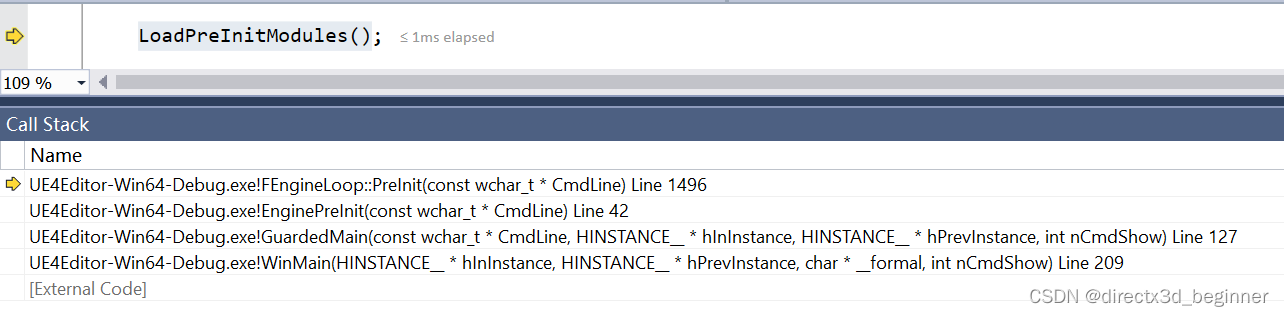
3,预初始化(一)(大象无形9.2)
正如书中所说,预初始化流程由FEngineLoop::PreInit()所实现 主要处理流程 1,设置路径:当前程序路径,当前工作目录路径,游戏的工程路径 2,设置标准输出:设置GLog系统输出的设备,是输出到命令行…...
)
【PAT甲级题解记录】1013 Battle Over Cities (25 分)
【PAT甲级题解记录】1013 Battle Over Cities (25 分) 前言 Problem:1013 Battle Over Cities (25 分) Tags:DFS 连通图 Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1013 Battle Over Cities (25 分) 问题描述 给…...

CSS-关键帧动画
animation和transition的区别 相同点:都是随时间改变元素的属性值 不同点:transition需要触发一个时间(hover或者click事件)才会随时间改变其css属性;而animation在不需要触发任何事件的情况下也是可以显示的随时间变化来改变元素的css属性值,从而达到一种动画的效果,cs…...
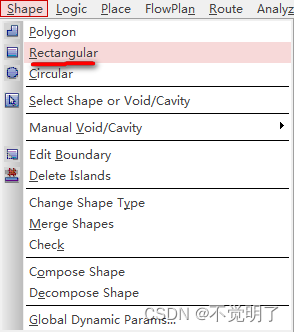
Allegro如何画Photoplot_Outline操作指导
Allegro如何画Photoplot_Outline操作指导 在用Allegro进行PCB设计的时候,最后进行光绘输出前,Photoplot_Outline是必备一个图形,所有在Photoplot_Outline中的图形将被输出,Photoplot_Outline以外的图形都将不被输出。 如何绘制Photoplot_Outline,具体操作如下 点击Shape点…...

ChatGPT对于普通人有什么机会和影响?
ChatGPT爆火“出圈”,短短三个月里,势如破竹。 月活已经达到1亿,什么概念呢?Tiktok在海外达到1亿月活用了将近9个月时间,Instagram用了大约2年半,就连比尔盖茨都表示“Web3没那么重要,元宇宙没…...

【人工智能 AI】可以从 RPA 中受益的 10 个行业 10 Industries That Can Benefit From RPA
目录 RPA技术介绍 Which industries can use robotic process automation?哪些行业可以使用机器人过程自动化? Robotic process automation in the retail industry零售业中的机器人过程自动化 Robotic process automation in the construction industry建筑行业的机器人…...

PHP 程序如何实现加密解密?
PHP 中有很多加密和解密的函数可用,以下是一些常用的加密解密方式和函数:对称加密:对称加密是一种加密方式,使用同一个密钥加密和解密数据。PHP 中可用的对称加密算法包括 AES、DES、3DES 等。以下是一些常用的对称加密函数&#…...
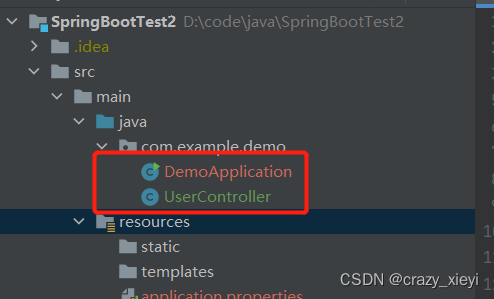
使用IDEA社区版如何创建SpringBoot项目?
Spring Boot 就是 Spring 框架的脚⼿架,它就是为了快速开发 Spring 框架⽽诞⽣的。首先谈谈SpringBoot的优点:1.快速集成框架,Spring Boot 提供了启动添加依赖的功能,⽤于秒级集成各种框架。 2.内置运⾏容器,⽆需配置 …...
)
HTML、CSS学习笔记3(平面转换:位移、旋转、缩放,渐变)
1.平面转换 使用 transform 属性实现元素的位移、旋转、缩放等效果 2D转换 2D转换是改变标签在二维平面上的位置和形状 移动:translate 旋转:rotate 缩放:scale 1.1位移translate translate语法 x就是X轴上水平移动,正向为右…...

【C语言经典例题】打印菱形
目录 一、题目要求 二、解题思路 上半部分三角形 打印空格 打印星号* 下半部分三角形 打印空格 打印星号* 三、完整代码 代码 运行截图: 一、题目要求 输入一个整数n(n为奇数),n为菱形的高,打印出该菱形 例&a…...
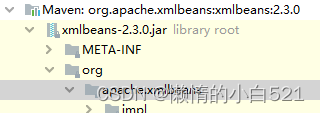
easyExcel与poi版本不兼容导致的后台报错问题
1、背景:最新接手公司系统excel导入解析模块,点击批量导入,后台报错如下 com.alibaba.excel.exception.ExcelAnalysisException: java.lang.NoClassDefFoundError: org/apache/poi/poifs/filesystem/FileMagicat com.alibaba.excel.analysis.…...
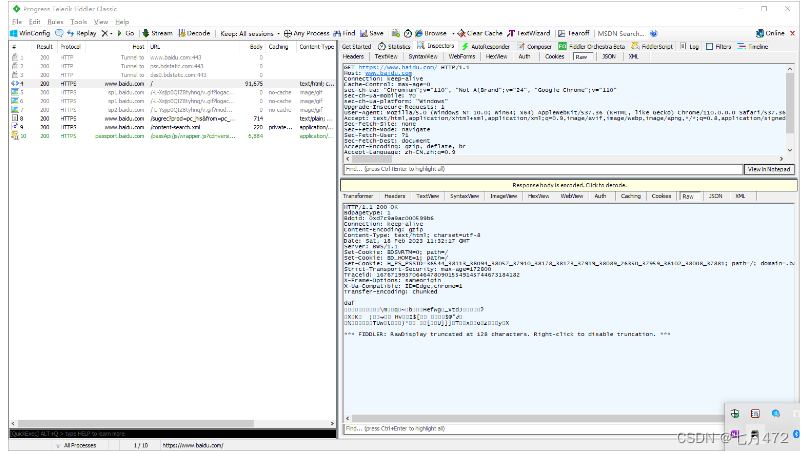
Fiddler报文分析-断点应用、模拟网络限速-HTTPS的 拦截
目录 一、报文分析 Statistics 请求性能数据 检查器(Inspectors) 自定义响应(AutoResponder) Composer Composer的功能就是用来创建HTTP Request然后发送请求。 允许自定义请求发送到服务器,即可以手动创建一个新…...
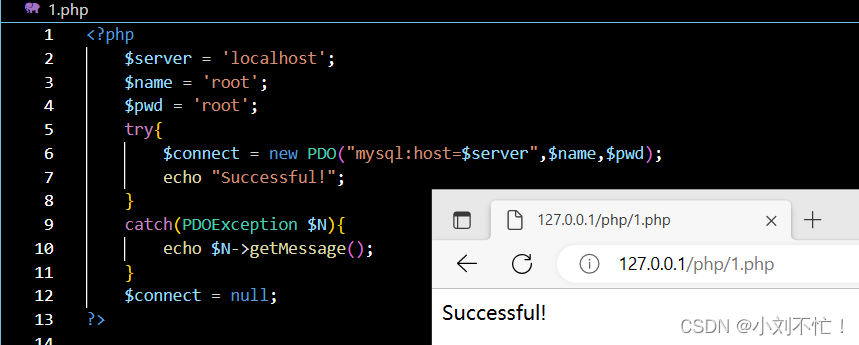
PHP基础(3)
PHP基础表单提交文件处理PHP连接数据库异常抛出表单提交 PHP通过全局变量 $_GET和 $_POST来收集表单数据。 接下来改用post方式进行提交,再次查看是否隐藏了提交的内容: 发现提交的信息已经不在链接之中进行显示了。 GET与POST区别在于一个会在连接…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
