一篇文章讲明白double、float丢失精度的问题
1.背景
1.1+0.1 = 1.2000000000000002
发现上面计算的值竟然和数学计算不一致
2. 问题
计算机是通过二进制计算的,如果我们在二进制的视角来看待上面问题,就很容易发现问题了。
例如:把「0.1」转成二进制的表示,然后还原成十进制,就能看出问题。
3. 0.1转二进制
小数转二进制,是通过除法进行的
0.1 = 1 ÷ 10
很简单,二进制就是要算
1 ÷ 1010
最终0.1转二进制是:0.0001100110011001100110011001100110011001100110011001101
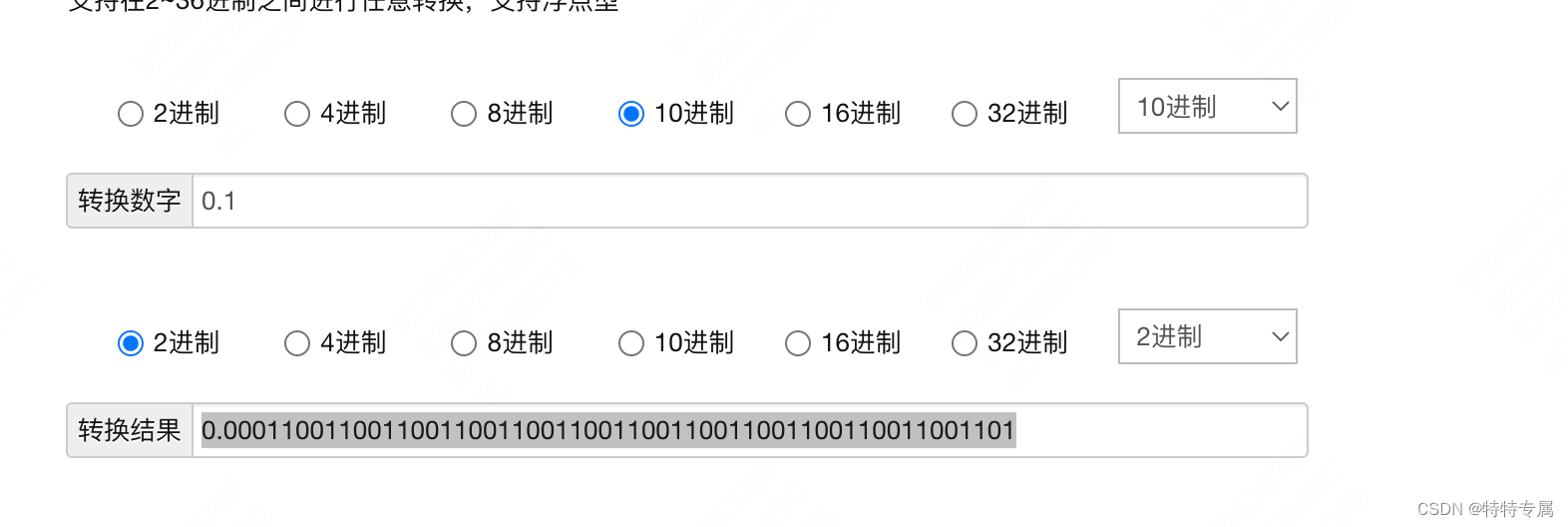
4.转换成对应精度数值
float的精度为7~8位有效数字,7位肯定能保证,8位的值也存在。
double的精度为16~17位有效数字
所以
二进制展示
1.1+0.1 = 1.0011001100110011001100110011001100110011001100110100
十进制展示
1.1+0.1 = 1.2000000000000002
5.解决方案
针对浮点数丢失精度的问题,我们可以通过BigDecimal来解决
new BigDecimal(double val)
该方法是不可预测的,以0.1为例,你以为你传了一个double类型的0.1,最后会返回一个值为0.1的BigDecimal吗?不会的,原因在于,0.1无法用有限长度的二进制数表示,无法精确地表示为双精度数,最后的结果会是0.100000xxx。
new BigDecimal(String val)
该方法是完全可预测的,也就是说你传入一个字符串"0.1",他就会给你返回一个值完全为0,1的BigDecimal,官方也表示,能用这个构造函数就用这个构造函数叭。
BigDecimal.valueOf(double val)
第二种构造方式已经足够优秀,可你还是想传入一个double值,怎么办呢?官方其实提供给你思路并且实现了它,可以使用Double.toString(double val)先将double值转为String,再调用第二种构造方式,你可以直接使用静态方法:valueOf(double val)。
总结:将double转为BigDecimal的时候,需要先把double转换为字符串,然后再作为BigDecimal(String val)构造函数的参数,这样才能避免出现精度问题。
相关文章:

一篇文章讲明白double、float丢失精度的问题
1.背景 1.10.1 1.2000000000000002 发现上面计算的值竟然和数学计算不一致 2. 问题 计算机是通过二进制计算的,如果我们在二进制的视角来看待上面问题,就很容易发现问题了。 例如:把「0.1」转成二进制的表示,然后还原成十进制&…...

Day 2 Qt
#include "my_widget.h" #include "ui_my_widget.h"My_Widget::My_Widget(QWidget *parent): QWidget(parent), ui(new Ui::My_Widget) {ui->setupUi(this);//窗口的相关设置 // this -> resize(800,500);this -> setWindowTitle("QQ聊天…...
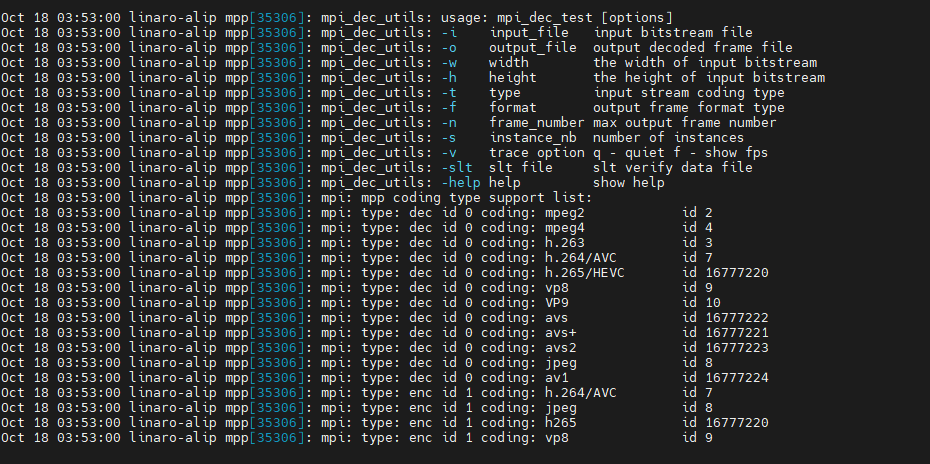
ArmSoM-W3之RK3588 MPP环境配置
1. 简介 瑞芯微提供的媒体处理软件平台(Media Process Platform,简称 MPP)是适用于瑞芯微芯片系列的 通用媒体处理软件平台。该平台对应用软件屏蔽了芯片相关的复杂底层处理,其目的是为了屏蔽不 同芯片的差异,为使用者…...

【C++ 拷贝构造函数详解】
在 C 编程中,拷贝构造函数是一个重要的概念,用于创建一个对象的副本。拷贝构造函数允许你在不改变原始对象的情况下创建一个新的对象,这在很多情况下非常有用。在本篇博客中,我们将详细讨论 C 拷贝构造函数的用法和实现。 什么是…...
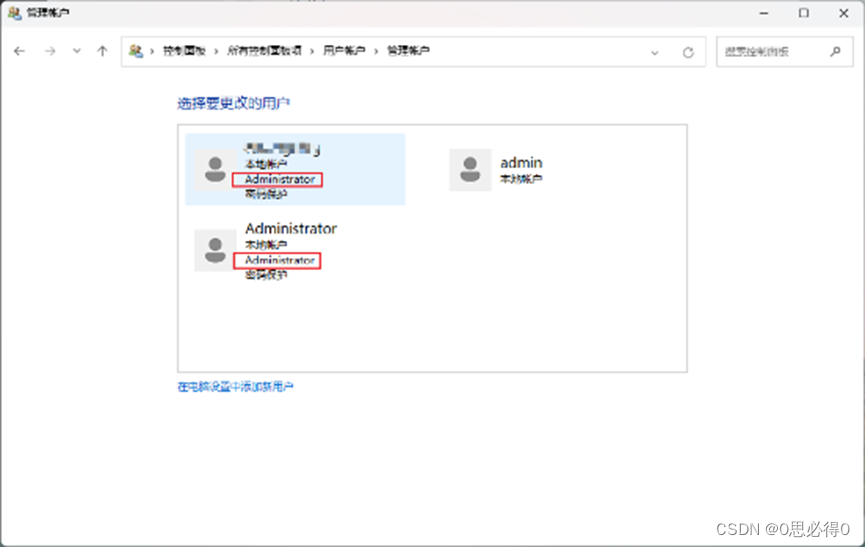
[计算机提升] 用户和用户组
1.1 用户和用户组 1.1.1 用户 用户账户是计算机操作系统中用于标识和管理用户身份的概念。 每个用户都拥有一个唯一的用户账户,该账户包含用户的登录名、密码和其他与用户身份相关的信息。 用户账户通常用于验证用户身份,并授权对系统资源的访问权限。…...
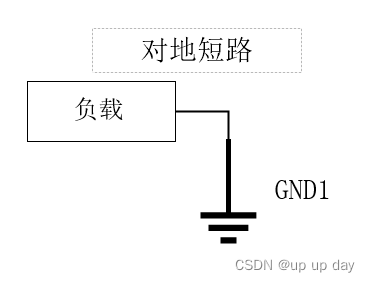
开路、断路和短路区别
文章目录 开路和断路击穿电源短路、用电器短路、对地短路和对电源短路 开路和断路 开路和断路是电路中两种用于描述电流流动情况的状态。 两者易混淆,常被混淆使用,但是它们还是有所不同。 开路表示电路中存在一个断链,电流无法从一个点流到…...

springBoot web开发自动配置和默认效果
web开发自动配置和默认效果 自动配置默认配置 自动配置 绑定了配置文件的一堆配置项 1、springMVC的所有配置 spring.mvc 2、Web场景通用配置 spring.web 3、文件上传配置 spring.servlet.multipart 4、服务器的配置serve: 比如:编码方式等 默认配置 重要…...
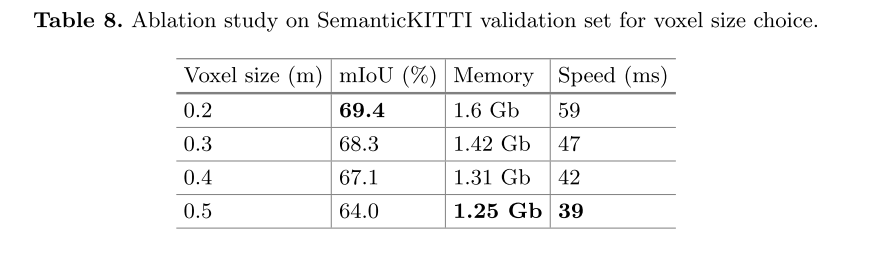
论文阅读:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks
来源:ECCV2022 链接:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks | SpringerLink 0、Abstract 在点云学习中,稀疏性和几何性是两个核心特性。近年来,为了提高点云语义分割的性能,人们提…...
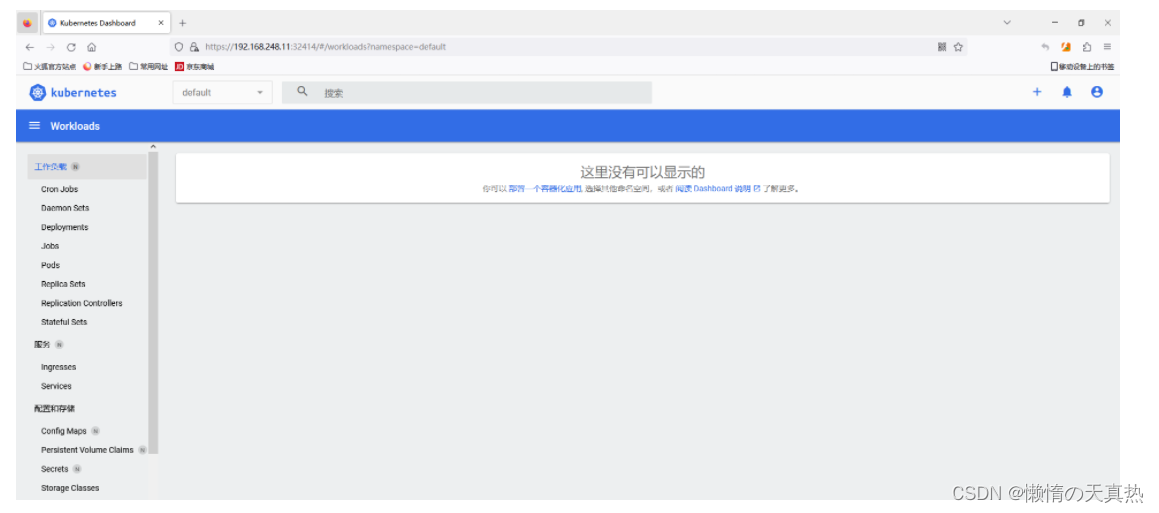
1-k8s1.24-底座搭建-基于containerd
文章目录 一、服务器准备二、安装Containerd三、安装k8s四、安装部署dashboard ps:第一遍搭建ks8的时候,由于k8s在1.24版本之后就放弃了对docker的支持,如果要继续使用docker需要自己加载插件。所以一开始就是直接使用 k8s1.24containerd进行…...

Java文件前后端上传下载工具类
任何非压缩格式下载 package com.pisx.pd.eco.util;import java.io.*; import java.util.Collections; import java.util.HashMap; import java.util.Map;import javax.servlet.ServletOutputStream; import javax.servlet.http.HttpServletResponse;import org.springframewo…...

内燃机可变气门驱动研究进展
Review of Advancement in Variable Valve Actuation of Internal Combustion Engines AbstractIntroduction燃烧和气体交换需要电子控制 paper Abstract 近年来,人们对空气污染和能源使用的日益关注导致了车辆动力总成系统的电气化。 另一方面,一个多世…...

NEFU离散数学实验2-容斥原理
相关概念 离散数学中的容斥原理是一种使用集合运算的技巧,通常用于计算两个或更多集合的并集或交集的大小。以下是一些与容斥原理相关的常见概念和公式。 概念: 1. 集合:由元素组成的对象,通常用大写字母表示,如A、B、…...
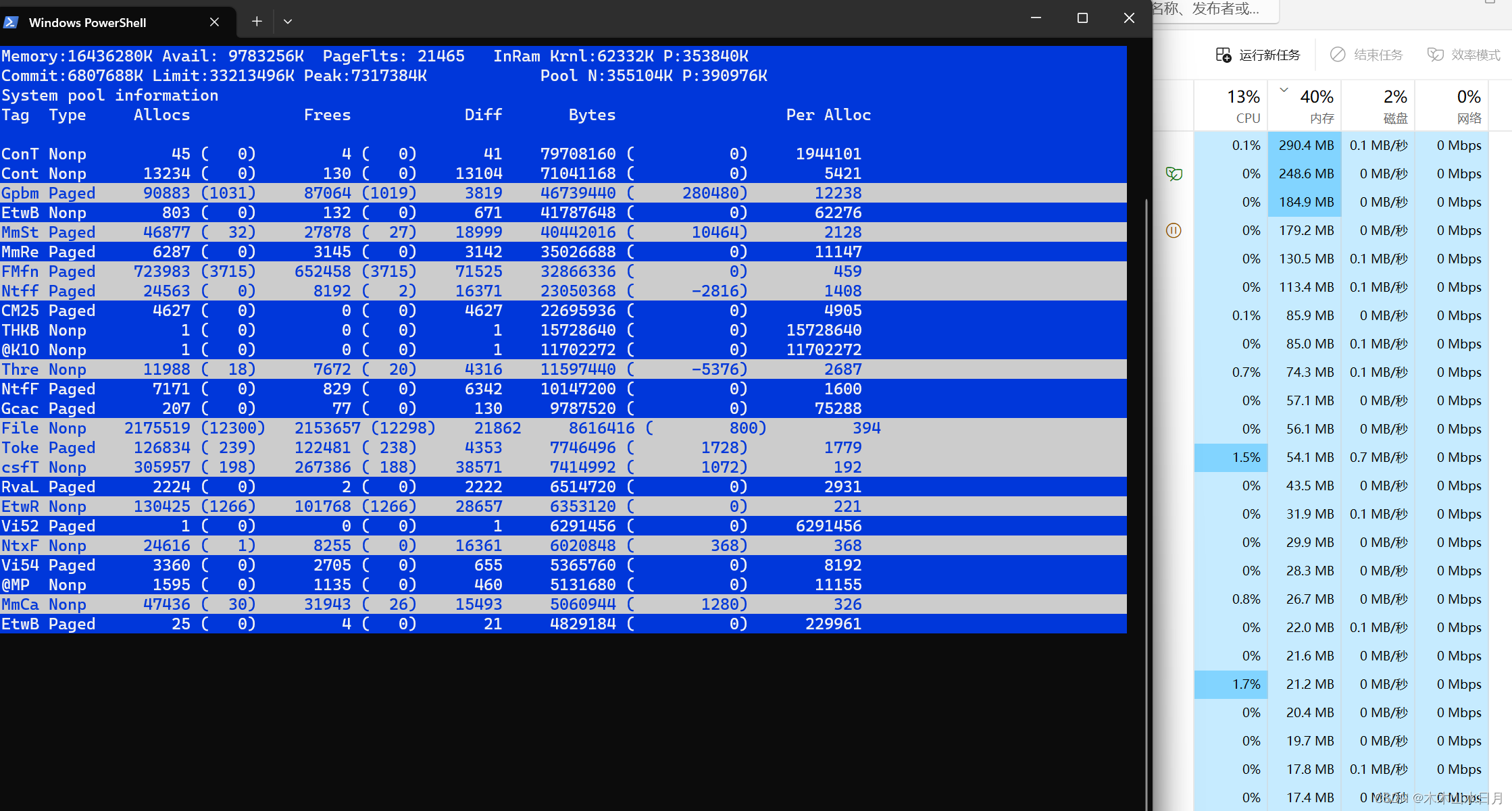
解决Windows内存溢出/占满死机问题-PoolMon工具
某一天, 工作所用笔记本突然越来越卡直至死机 以为只是windows11的抽风行为,之前就因为windows11资源管理器经常卡死(后升级小版本好多了)。 遂长按电源键强制关机重启。 然慢慢又越来越卡,直至卡死,无…...
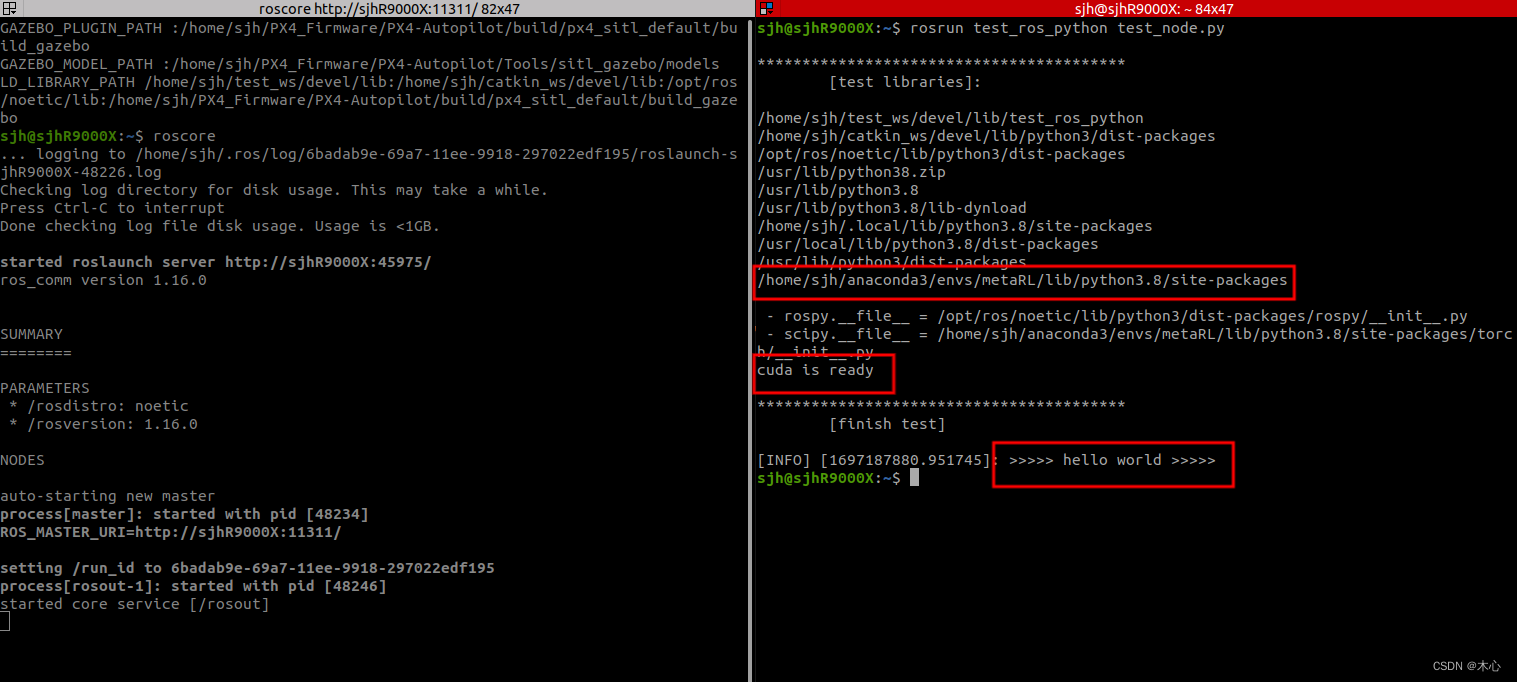
【ROS】ros-noetic和anaconda联合使用【教程】
【ROS】ros-noetic和anaconda联合使用【教程】 文章目录 【ROS】ros-noetic和anaconda联合使用【教程】1. 安装anaconda2. 创建虚拟环境3. 查看python解释器路径4. 在虚拟环境中使用任意的包5. 创建工作空间和ros功能包进行测试Reference 1. 安装anaconda 在Ubuntu20.04中安装…...

自动化RPA开发 --获取所有窗口信息和进程信息
场景 准备做一个RPA工具,可以从桌面和浏览器选择元素,获取窗口信息和进程信息是必要的,因为获取了窗口信息和进程,可用对程序做一些想要的操作。 coding 工具类 /*** Windows系统工具类*/ public class WinOsUtils {static fi…...

【Qt之布局】QVBoxLayout、QHBoxLayout、QGridLayout、QFormLayout介绍及使用
在Qt中,布局管理器(Layout)用于管理窗口中的控件的位置和大小,以适应不同大小的窗口。 常用的布局管理器包括QVBoxLayout、QHBoxLayout、QGridLayout和QFormLayout。 先放张布局UI: 1. QVBoxLayout(垂直布…...
【计算机毕业设计】python在线课程培训学习考试系统637r7-PyCharm项目
使用说明 使用Navicat或者其它工具,在mysql中创建对应名称的数据库,并导入项目的sql文件; 使用PyCharm 导入项目,修改配置,运行项目; 将项目中config.ini配置文件中的数据库配置改为自己的配置,…...
vue3后台管理系统之登录界面和业务的实现
1.静态页面的搭建 <template><div class"login_container"><el-row><el-col :span"12" :xs"0" /><el-col :span"12" :xs"24"><!-- 登录的表单 --><el-form ref"loginForms&qu…...
GEE19:基于Landsat8的常见的植被指数逐年获取
植被指数逐年获取 1. 常见的植被指数1.1 比值植被指数(Ratio vegetation index,RVI)1.2 归一化植被指数(Normalized Difference Vegetation Index,NDVI)1.3 增强植被指数(Enhanced Vegetation I…...

Python【多分支实际应用的练习】
要求:某商店T恤的价格为35元/件(2件9折,3件以上8折),裤子的价格为120 元/条(2条以上9折)小明在该店买了3件T恤和2条裤子,请计算并显示小明应该付多少钱? 代码如下: tshirt_price 35 # T恤的单价 pan…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
