数组(二)-- LeetCode[303][304] 区域和检索 - 数组不可变
1 区域和检索 - 数组不可变
1.1 题目描述

题目链接:https://leetcode.cn/problems/range-sum-query-immutable/
1.2 思路分析
最朴素的想法是存储数组 nums 的值,每次调用 sumRange 时,通过循环的方法计算数组 nums 从下标 iii 到下标 jjj 范围内的元素和,需要计算 j−i+1j−i+1j−i+1 个元素的和。由于每次检索的时间和检索的下标范围有关,因此检索的时间复杂度较高,如果检索次数较多,则会超出时间限制。
由于会进行多次检索,即多次调用 sumRange,因此为了降低检索的总时间,应该降低 sumRange 的时间复杂度,最理想的情况是时间复杂度 O(1)O(1)O(1)。为了将检索的时间复杂度降到 O(1)O(1)O(1),需要在初始化的时候进行预处理。
注意到当 i≤ji≤ji≤j 时,sumRange(i,j) 可以写成如下形式:
sumRange(i,j)=∑k=ijnums[k]=∑k=0jnums[k]−∑k=0i−1nums[k]\begin{aligned} & \operatorname{sum} \operatorname{Range}(i, j) \\ = & \sum_{k=i}^j n u m s[k] \\ = & \sum_{k=0}^j n u m s[k]-\sum_{k=0}^{i-1} n u m s[k]\end{aligned}==sumRange(i,j)k=i∑jnums[k]k=0∑jnums[k]−k=0∑i−1nums[k]
由此可知,要计算 sumRange(i,j),则需要计算数组 nums 在下标 jjj 和下标 i−1i−1i−1 的前缀和,然后计算两个前缀和的差。
如果可以在初始化的时候计算出数组 nums 在每个下标处的前缀和 pre_sum,即可满足每次调用 sumRange 的时间复杂度都是 O(1)O(1)O(1)。
示例代码:
class NumArray:def __init__(self, nums: List[int]):self.pre_sum = [0] # 便于计算累加和,若直接分配数组空间,计算效率更高for i in range(len(nums)):self.pre_sum.append(self.pre_sum[i] + nums[i]) # 计算nums累加和def sumRange(self, left: int, right: int) -> int:return self.pre_sum[right+1] - self.pre_sum[left]
下面以数组 [1, 12, -5, -6, 50, 3] 为例,展示了求 pre_sum 的过程。

复杂度分析
- 时间复杂度:初始化 O(n)O(n)O(n),每次检索 O(1)O(1)O(1),其中 nnn 是数组 nums 的长度。初始化需要遍历数组 nums 计算前缀和,时间复杂度是 O(n)O(n)O(n)。每次检索只需要得到两个下标处的前缀和,然后计算差值,时间复杂度是 O(1)O(1)O(1)。
- 空间复杂度:O(n)O(n)O(n),其中 nnn 是数组 nums 的长度。需要创建一个长度为 n+1n+1n+1 的前缀和数组。
2 二维区域和检索 - 矩阵不可变
2.1 题目描述

题目链接:https://leetcode.cn/problems/range-sum-query-2d-immutable/
2.2 思路分析
这部分借鉴自:笨猪爆破组的题解————从暴力法开始优化 「二维前缀和」做了什么事 | leetcode.304
1. 暴力法
对二维矩阵,求子矩阵 (n∗m)(n*m)(n∗m) 的和。两重循环,累加求和。
每次查询时间复杂度 O(n∗m)O(n∗m)O(n∗m),n和m是子矩阵的行数和列数。查询的代价大。
2. 第一步优化
上面的暴力法其实也分了 n 步:第一行的求和,到第 n 行的求和,它们是 n 个一维数组。
昨天我们学习了一维前缀和,我们可以对这n个一维数组求前缀和,得到n个一维pre_sum数组。
为了节省查询的时间,我们求出整个矩阵每一行的一维pre_sum数组
根据前缀和定义:pre_sum[i]=nums[0]+nums[1]+⋯+nums[i]{pre}\_{sum}[i]=nums[0]+nums[1]+\cdots+nums[i]pre_sum[i]=nums[0]+nums[1]+⋯+nums[i],求出前缀和(下图红字):

然后套用通式:nums[i]+⋯+nums[j]=pre_sum[j]−pre_sum[i−1]nums[i]+\cdots+nums[j]=pre\_sum[j]-pre\_sum[i-1]nums[i]+⋯+nums[j]=pre_sum[j]−pre_sum[i−1]
即可求出粉色子阵列的和,计算情况如下图。

可见,如果想多次查询子阵列的和,我们可以提前求出每一行数组的一维前缀和。
那么查询阶段,求出一行子数组的求和,就只是 O(1)O(1)O(1),查询 n 行的子阵列,每次就查询花费 O(n)O(n)O(n),比 O(n2)O(n^2)O(n2) 好
3. 示例代码:
class NumMatrix:def __init__(self, matrix: List[List[int]]):m, n = len(matrix), len(matrix[0]) # 矩阵的行和列self.pre_sum = [[0] for _ in range(m)] # 构造一维前缀和矩阵for i in range(m):for j in range(n):self.pre_sum[i].append(self.pre_sum[i][j]+matrix[i][j])def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:return sum([self.pre_sum[i][col2+1]-self.pre_sum[i][col1] for i in range(row1, row2+1)])
4. 第二步优化
还可以继续优化吗?
我们引入一个概念:二维前缀和,定义式如下

pre_sum[i][j] 表示:左上角为 arr[0][0],右下角为 arr[i][j] 的阵列的求和.
我们把这个阵列拆分成四个部分,如图中的色块。
要想求出 pre_sum[i][j],根据上图,由容斥原理,有:

移项后:
arr[i][j]=pre_sum[i][j]+pre_sum[i−1][j−1]−pre_sum[i−1][j]−pre_sum[i][j−1]arr[i][j] = pre\_sum[i][j] + pre\_sum[i-1][j-1] - pre\_sum[i-1][j] - pre\_sum[i][j-1]arr[i][j]=pre_sum[i][j]+pre_sum[i−1][j−1]−pre_sum[i−1][j]−pre_sum[i][j−1]
现在想求:行 从 a 到 A,列 从 b 到 B 的子阵列的和。叠加上式,各种相消后。得:

回到粉色子阵列,求她的和,就是如下图的 4 个 pre_sum 矩阵元素相加减。

问题来了,怎么求出 pre_sum 二维阵列的每一项?
就是用遍历原矩阵,两层循环,套下图的公式。
注意到上图黄字,在 -1 位置上预置了 0,只是为了让处于边界的 preSum 元素,也能套用下面的通式。

两个关键式 pre_sum[i][j] 的定义式如下,并且预置 pre-sum[-1][j] 和 pre_sum[i][-1] 为 0:
preSum[i][j]=∑x=0i∑y=0jarr[x][y]\operatorname{preSum}[i][j]=\sum_{x=0}^i \sum_{y=0}^j \operatorname{arr}[x][y] preSum[i][j]=x=0∑iy=0∑jarr[x][y]
求:行从 a 到 A,列从 b 到 B 的子阵列的和的通式:
∑i=aA∑i=bBarr[i][j]=pre_sum[A][B]+pre_sum[a−1][b−1]−pre_sum[A][b−1]−pre_sum[a−1][B]\sum_{i=a}^A \sum_{i=b}^B \operatorname{arr}[i][j]=\operatorname{pre\_sum}[A][B]+\operatorname{pre\_sum}[a-1][b-1]-\operatorname{pre\_sum}[A][b-1]-\operatorname{pre\_sum}[a-1][B] i=a∑Ai=b∑Barr[i][j]=pre_sum[A][B]+pre_sum[a−1][b−1]−pre_sum[A][b−1]−pre_sum[a−1][B]
查询的时间复杂度降下来了
因此子阵列的求和,都只需要访问二维 pre_sum 数组的四个值。
预处理阶段,求出二维 pre_sum 数组,需要花费 O(n∗m)O(n∗m)O(n∗m),n和m是子矩阵的行数和列数。
但之后每次查询,就都是 O(1)O(1)O(1) 的时间复杂度
5. 调整 pre_sum 矩阵
为了减少特判的代码,我们调整一下 pre_sum 矩阵,原先 arr[i][j] 对应 pre_sum[i][j]
现在错开,arr[i][j] 对应 pre_sum[i+1][j+1]。
如下图所示,pre_sum 阵列会比原矩阵多一行一列,为了让 pre_sum 的 -1 列 -1 行变成 0 行 0 列

现在 preSum[i][j] 的定义式,改一下
pre_sum[i+1][j+1]=∑x=0i∑y=0jarr[x][y]\operatorname{pre\_sum}[i+1][j+1]=\sum_{x=0}^i \sum_{y=0}^j \operatorname{arr}[x][y] pre_sum[i+1][j+1]=x=0∑iy=0∑jarr[x][y]
并且预置 pre_sum[0][j] 和 pre_sum[i][0] 为 0
求:行从 a 到 A,列从 b 到 B 的子阵列的和,的通式,改一下:
∑i=aA∑i=bBarr[i][j]=pre_sum[A+1][B+1]+pre_sum[a][b]−pre_sum[A+1][b]−pre_sum[a][B+1]\sum_{i=a}^A \sum_{i=b}^B \operatorname{arr}[i][j]=\operatorname{pre\_sum}[A+1][B+1]+\operatorname{pre\_sum}[a][b]-\operatorname{pre\_sum}[A+1][b]-\operatorname{pre\_sum}[a][B+1] i=a∑Ai=b∑Barr[i][j]=pre_sum[A+1][B+1]+pre_sum[a][b]−pre_sum[A+1][b]−pre_sum[a][B+1]
6. 示例代码:
class NumMatrix:def __init__(self, matrix: List[List[int]]):m, n = len(matrix), len(matrix[0]) # 矩阵的行和列self.pre_sum = [[0]*(n+1) for _ in range(m+1)] # 构造一维前缀和矩阵for i in range(m):for j in range(n):self.pre_sum[i+1][j+1] = self.pre_sum[i+1][j] + self.pre_sum[i][j+1] - self.pre_sum[i][j] + matrix[i][j]def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:return (self.pre_sum[row2+1][col2+1] - self.pre_sum[row1][col2+1] - self.pre_sum[row2+1][col1] + self.pre_sum[row1][col1])
7. 复杂度分析
- 时间复杂度:初始化 O(mn)O(mn)O(mn),每次检索 O(1)O(1)O(1),其中 m 和 n 分别是矩阵 matrix 的行数和列数。初始化需要遍历矩阵 matrix 计算二维前缀和,时间复杂度是 O(mn)O(mn)O(mn)。每次检索的时间复杂度是 O(1)O(1)O(1)。
- 空间复杂度:O(mn)O(mn)O(mn),其中m和n分别是矩阵 matrix 的行数和列数。需要创建一个 m+1 行 n+1 列的二维前缀和数组 pre_sum。
做题心得:以后会不会延伸到张量呢,更高维数的也是总结通式,就比如三维是一个立方体,依然是计算每个小立方体的和。
相关文章:

数组(二)-- LeetCode[303][304] 区域和检索 - 数组不可变
1 区域和检索 - 数组不可变 1.1 题目描述 题目链接:https://leetcode.cn/problems/range-sum-query-immutable/ 1.2 思路分析 最朴素的想法是存储数组 nums 的值,每次调用 sumRange 时,通过循环的方法计算数组 nums 从下标 iii 到下标 jjj …...
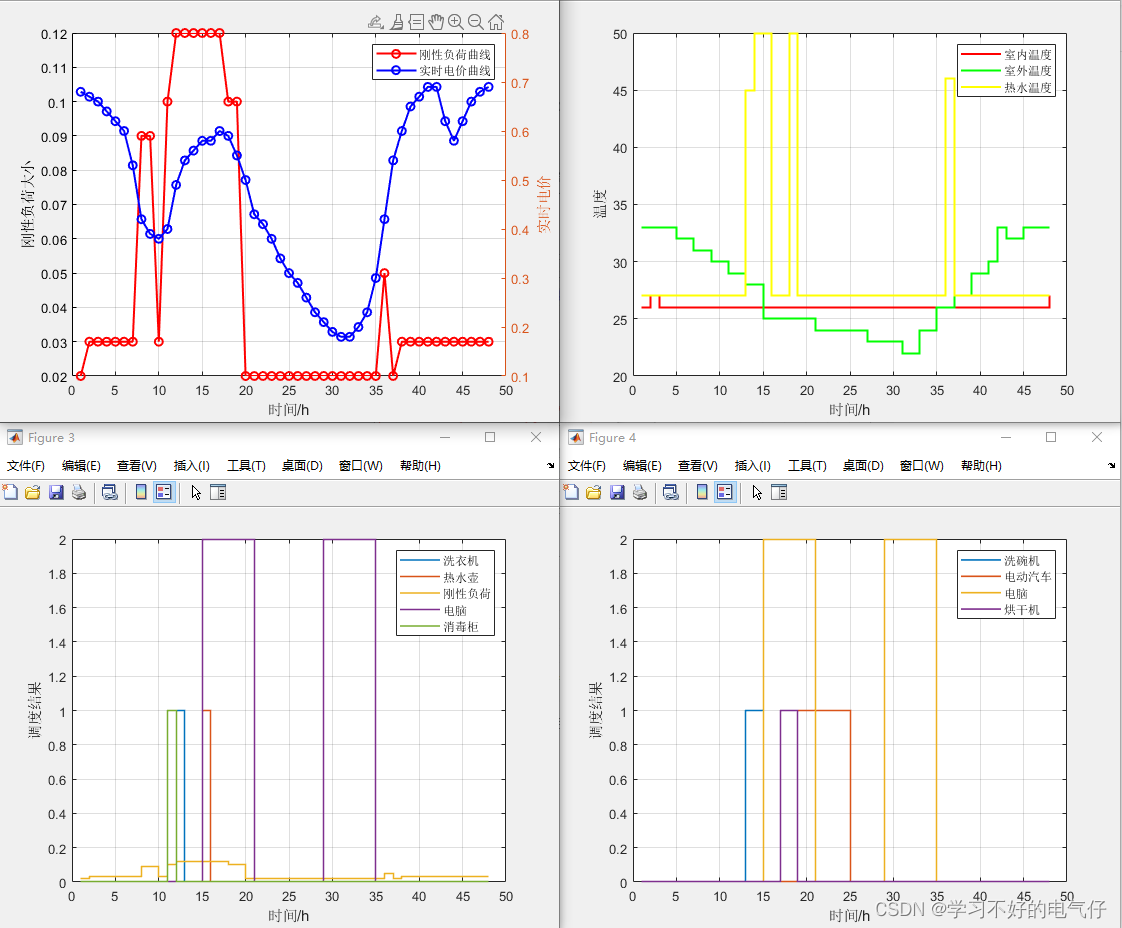
22-基于分时电价条件下家庭能量管理策略研究MATLAB程序
参考文献:《基于分时电价和蓄电池实时控制策略的家庭能量系统优化》参考部分模型《计及舒适度的家庭能量管理系统优化控制策略》参考部分模型主要内容:主要做的是家庭能量管理模型,首先构建了电动汽车、空调、热水器以及烘干机等若干家庭用户…...
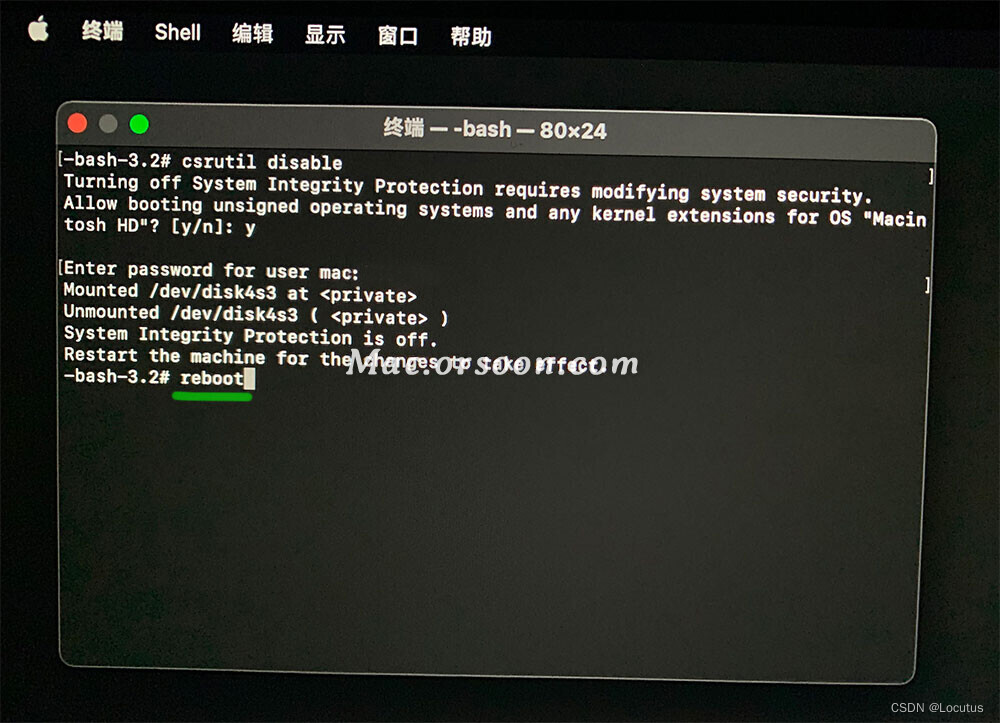
“XXX.app 已损坏,打不开。您应该将它移到废纸篓”,Mac应用程序无法打开或文件损坏的处理方法(2)
1. 检查状态 在sip系统完整性关闭前,我们先检查是否启用了SIP系统完整性保护。打开终端输入以下命令【csrutil status】并回车: 你会看到以下信息中的一个,用来指示SIP状态。已关闭 disabled: System Integrity Protection status: disabl…...

flask入门-3.Flask操作数据库
3. Flask操作数据库 1. 连接数据库 首先下载 MySQL数据库 其次下载对应的包: pip install pymysql pip install flask-sqlalchemy在 app.py 中进行连接测试 from flask import Flask, request, render_template from flask_sqlalchemy import SQLAlchemyhostname "1…...
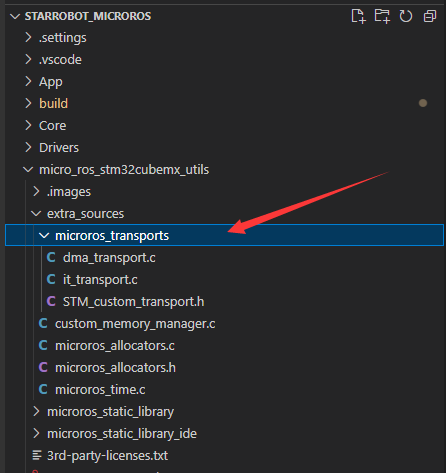
STM32 使用microros与ROS2通信
本文主要介绍如何在STM32中使用microros与ROS2进行通信,在ROS1中标准的库是rosserial,在ROS2中则是microros,目前网上的资料也有一部分了,但是都没有提供完整可验证的demo,本文将根据提供的demo一步步给大家进行演示。1、首先如果你用的不是S…...

51单片机入门 - 测试:SDCC / Keil C51 会让没有调用的函数参与编译吗?
Small Device C Compiler(SDCC)是一款免费 C 编译器,适用于 8 位微控制器。 不想看测试过程的话可以直接划到最下面看结论:) 关于软硬件环境的信息: Windows 10STC89C52RCSDCC (构建HEX文件&…...

【计算机网络】计算机网络
目录一、概述计算机网络体系结构二、应用层DNS应用文件传输应用DHCP 应用电子邮件应用Web应用当访问一个网页的时候,都会发生什么三、传输层UDP 和 TCP 的特点UDP 首部格式TCP 首部格式TCP 的三次握手TCP 的四次挥手TCP 流量控制TCP 拥塞控制三、网络层IP 数据报格式…...
【java web篇】项目管理构建工具Maven简介以及安装配置
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
springboot笔记
微服务架构 微服务是一种架构风格,开发构建应用的时候把应用的业务构建成一个个的小服务(这就类似于把我们的应用程序构建成了一个个小小的盒子,它们在一个大的容器中运行,这种一个个的小盒子我们把它叫做服务)&#…...
【多线程与高并发】- 浅谈volatile
浅谈volatile简介JMM概述volatile的特性1、可见性举个例子总结2、无法保证原子性举个例子分析使用volatile对原子性测试使用锁的机制总结3、禁止指令重排什么是指令重排序重排序怎么提高执行速度重排序的问题所在volatile禁止指令重排序内存屏障(Memory Barrier)作用volatile内…...
avro格式详解
【Avro介绍】Apache Avro是hadoop中的一个子项目,也是一个数据序列化系统,其数据最终以二进制格式,采用行式存储的方式进行存储。Avro提供了:丰富的数据结构可压缩、快速的二进制数据格式一个用来存储持久化数据的容器文件远程过程…...

【涨薪技术】0到1学会性能测试 —— LR录制回放事务检查点
前言 上一次推文我们分享了性能测试分类和应用领域,今天带大家学习性能测试工作原理、事务、检查点!后续文章都会系统分享干货,带大家从0到1学会性能测试,另外还有教程等同步资料,文末免费获取~ 01、LR工作原理 通常…...

卡尔曼滤波原理及代码实战
目录简介1.原理介绍场景假设(1).下一时刻的状态(2).增加系统的内部控制(3).考虑运动系统外部的影响(4).后验估计:预测结果与观测结果的融合卡尔曼增益K2.卡尔曼滤波计算过程(1).预测阶段(先验估计阶段)(2).更新阶段(后验估计阶段&…...
Jmeter使用教程
目录一,简介二,Jmeter安装1,下载2,安装三,创建测试1,创建线程组2,创建HTTP请求默认值3,创建HTTP请求4,添加HTTP请求头5,添加断言6,添加查看结果树…...

论文笔记|固定效应的解释和使用
DeHaan E. Using and interpreting fixed effects models[J]. Available at SSRN 3699777, 2021. 虽然固定效应在金融经济学研究中无处不在,但许多研究人员对作用的了解有限。这篇论文解释了固定效应如何消除遗漏变量偏差并影响标准误差,并讨论了使用固…...
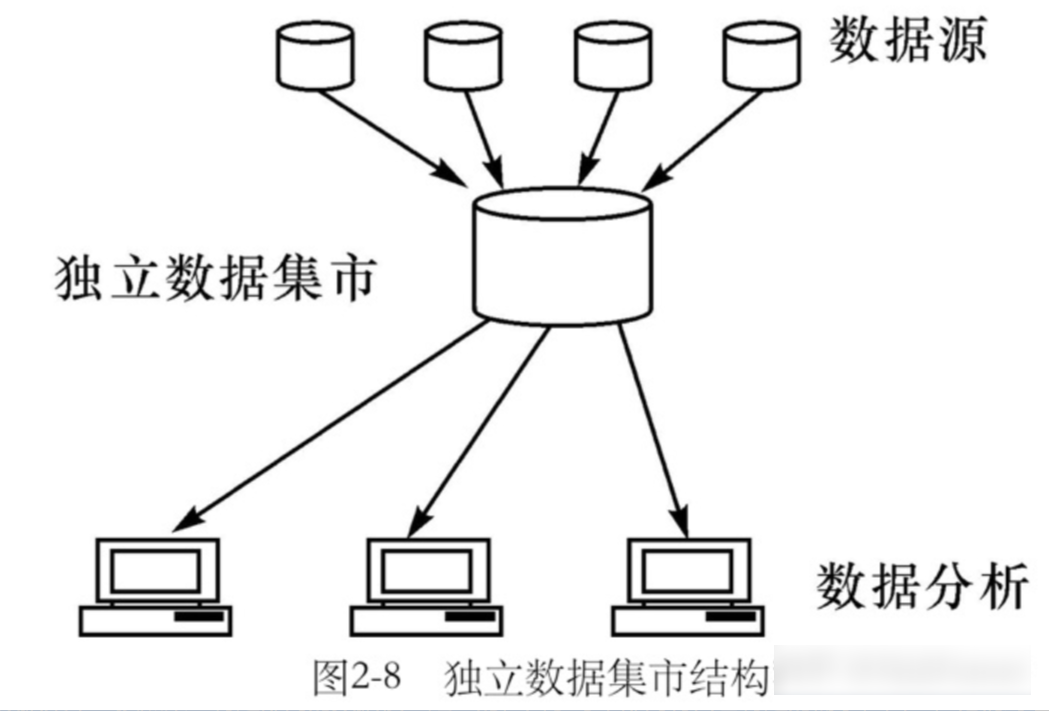
数据集市与数据仓库的区别
数据仓库是企业级的,能为整个企业各个部门的运作提供决策支持;而数据集市则是部门级的,一般只能为某个局部范围内的管理人员服务,因此也称之为部门级数据仓库。 1、两种数据集市结构 数据集市按数据的来源分为以下两种 &#x…...

Golang学习Day3
😋 大家好,我是YAy_17,是一枚爱好网安的小白。 本人水平有限,欢迎各位师傅指点,欢迎关注 😁,一起学习 💗 ,一起进步 ⭐ 。 ⭐ 此后如竟没有炬火,我便是唯一的…...
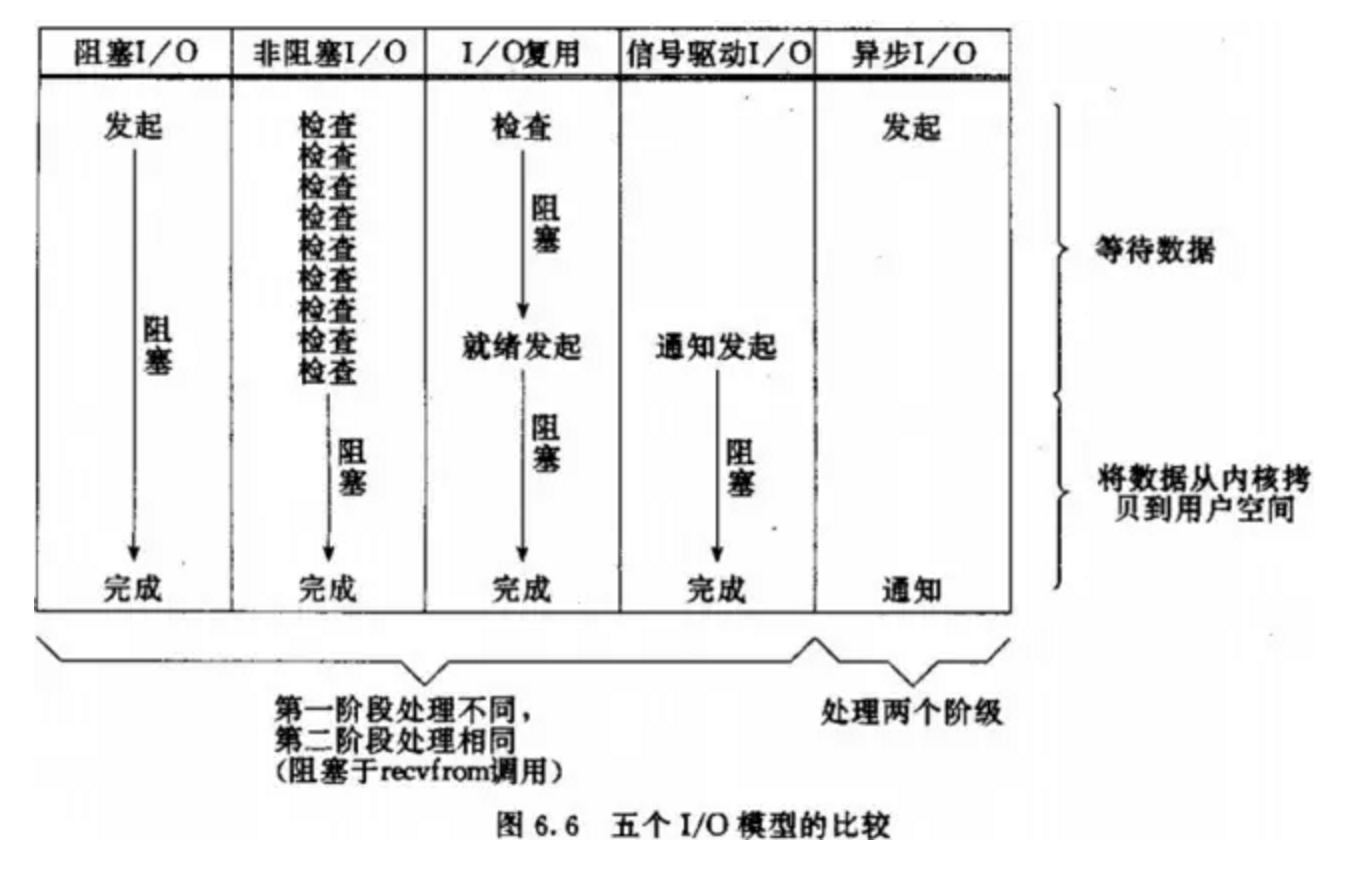
Python并发编程-事件驱动模型
一、事件驱动模型介绍 1、传统的编程模式 例如:线性模式大致流程 开始--->代码块A--->代码块B--->代码块C--->代码块D--->......---&…...
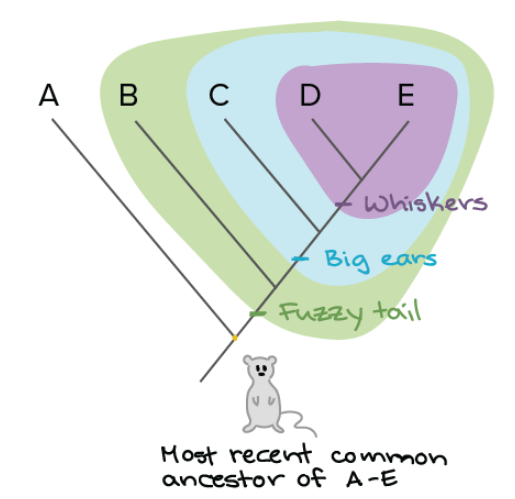
构建系统发育树简述
1. 要点 系统发育树代表了关于一组生物之间的进化关系的假设。可以使用物种或其他群体的形态学(体型)、生化、行为或分子特征来构建系统发育树。在构建树时,我们根据共享的派生特征(不同于该组祖先的特征)将物种组织成…...
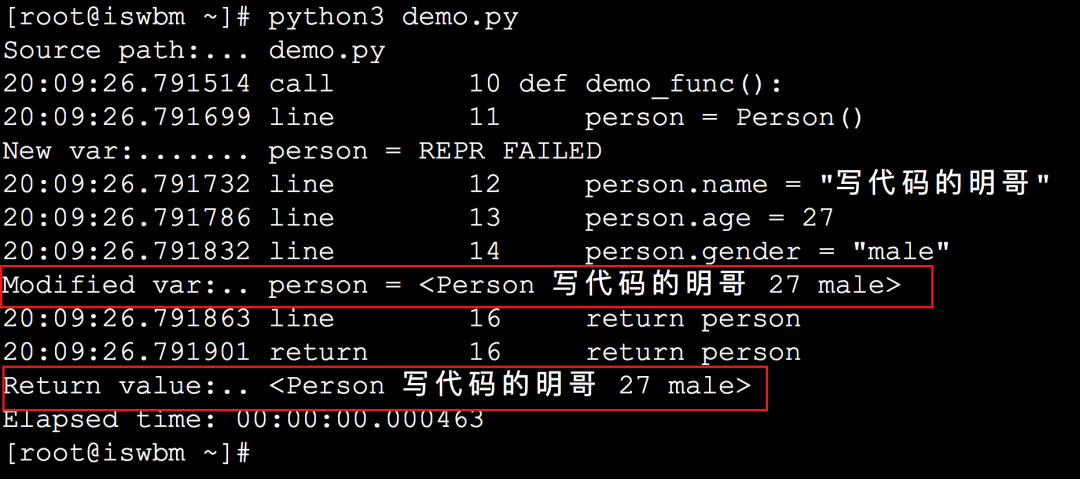
这款 Python 调试神器推荐收藏
大家好,对于每个程序开发者来说,调试几乎是必备技能。 代码写到一半卡住了,不知道这个函数执行完的返回结果是怎样的?调试一下看看 代码运行到一半报错了,什么情况?怎么跟预期的不一样?调试一…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
