CCF CSP认证 历年题目自练Day35
题目一
试题编号: 202305-1
试题名称: 重复局面
时间限制: 1.0s
内存限制: 512.0MB
问题描述:
题目背景
国际象棋在对局时,同一局面连续或间断出现3次或3次以上,可由任意一方提出和棋。
问题描述
国际象棋每一个局面可以用大小为 8*8的字符数组来表示,其中每一位对应棋盘上的一个格子。六种棋子王、后、车、象、马、兵分别用字母 k、q、r、b、n、p 表示,其中大写字母对应白方、小写字母对应黑方。棋盘上无棋子处用字符 * 表示。两个字符数组的每一位均相同则说明对应同一局面。
现已按上述方式整理好了每步棋后的局面,试统计每个局面分别是第几次出现。
输入格式
从标准输入读入数据。
输入的第一行包含一个正整数 n,表示这盘棋总共有 n 步。
接下来 8×n 行,依次输入第 1 到第 n 步棋后的局面。具体来说每行包含一个长度为 8 的字符串,每 8 行字符串共 64 个字符对应一个局面。
输出格式
输出到标准输出中。
输出共 n 行,每行一个整数,表示该局面是第几次出现。
样例输入
8
********
******pk
*****r*p
p*pQ****
********
**b*B*PP
****qP**
**R***K*
********
******pk
*****r*p
p*pQ****
*b******
****B*PP
****qP**
**R***K*
********
******pk
*****r*p
p*p*****
*b**Q***
****B*PP
****qP**
**R***K*
******k*
******p*
*****r*p
p*p*****
*b**Q***
****B*PP
****qP**
**R***K*
******k*
******p*
*****r*p
p*pQ****
*b******
****B*PP
****qP**
**R***K*
********
******pk
*****r*p
p*pQ****
*b******
****B*PP
****qP**
**R***K*
********
******pk
*****r*p
p*p*****
*b**Q***
****B*PP
****qP**
**R***K*
********
******pk
******rp
p*p*****
*b**Q***
****B*PP
****qP**
**R***K*
样例输出
1
1
1
1
1
2
2
1
样例说明
第 6、7 步后的局面分别与第 2、3 步后的局面相同。第 8 步后的局面与上图相对应。
子任务
输入数据满足 n≤100。
提示
判断重复局面仅涉及字符串比较,无需考虑国际象棋实际行棋规则。
题目分析(个人理解)
- 题目挺长,但是很水,直接看样例输入输出即可知道题意,就是第一行输入n个局面,一个局面有8行8列,输出每一个局面出现的次数。
- 我的核心思想是这样的,将每个局面存入一个容器,当再出现相同局面的时候计数器加一(将计数器的每一步都存入列表count[]),最后遍历输出count的元素即可。
- 第一种方法,我选择将每个局面用temp(str型)表示,并且全部存入列表l[],(用.append()方法追加写入)每追加写入一个局面就判断一次前面是否出现过,如果出现,计数器加一,存入存放计数器的列表。
- 上代码!!!
temp=''
l=[]
n=int(input())
count=[1]*n
for i in range(n):for j in range(8):temp+=input()l.append(temp)for x in range(i):if temp in l[x]:count[i]+=1temp=''
for i in count:print(i)- 当然用字典更简单一些,用字典的keys表示每一个局面,values表示出现的次数,只需要每一步都输出然后更新字典即可。
- 上代码!!!
n = int(input())
chess = {}
for i in range(n):temp = ''for j in range(8):temp += input()if temp not in chess:chess[temp] = 1else:chess[temp] += 1print(chess[temp])题目二
试题编号: 202305-2
试题名称: 矩阵运算
时间限制: 5.0s
内存限制: 512.0MB
问题描述:
题目背景

是 Transformer 中注意力模块的核心算式,其中 Q、K 和 V 均是 n 行 d 列的矩阵,KT 表示矩阵 K 的转置,× 表示矩阵乘法。
问题描述
为了方便计算,顿顿同学将 Softmax 简化为了点乘一个大小为 n 的一维向量 W:(W⋅(Q×KT))×V
点乘即对应位相乘,记 W(i) 为向量 W 的第 i 个元素,即将 (Q×KT) 第 i 行中的每个元素都与 W(i) 相乘。
现给出矩阵 Q、K 和 V 和向量 W,试计算顿顿按简化的算式计算的结果。
输入格式
从标准输入读入数据。
输入的第一行包含空格分隔的两个正整数 n 和 d,表示矩阵的大小。
接下来依次输入矩阵 Q、K 和 V。每个矩阵输入 n 行,每行包含空格分隔的 d 个整数,其中第 i 行的第 j 个数对应矩阵的第 i 行、第 j 列。
最后一行输入 n 个整数,表示向量 W。
输出格式
输出到标准输出中。
输出共 n 行,每行包含空格分隔的 d 个整数,表示计算的结果。
样例输入
3 2
1 2
3 4
5 6
10 10
-20 -20
30 30
6 5
4 3
2 1
4 0 -5
样例输出
480 240
0 0
-2200 -1100
子任务
70 的测试数据满足:n≤100 且 d≤10;输入矩阵、向量中的元素均为整数,且绝对值均不超过 30。
全部的测试数据满足:n≤104 且 d≤20;输入矩阵、向量中的元素均为整数,且绝对值均不超过 1000。
提示
请谨慎评估矩阵乘法运算后的数值范围,并使用适当数据类型存储矩阵中的整数。
题目分析(个人理解)
- 读到题目先和大家复习一下线性代数的矩阵转置,很简单一句话,行变列,列变行。设矩阵m* n则转置矩阵就是n*m。要求(W⋅(Q×KT))×V,再看输入只让输入k,那么必须要实现转置的操作,有以下几种方法实现:
- 第一种双重循环:
# python 双重循环arr = [[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9],[10, 11, 12]]arr2 = []
# 数组的第二维维度
for i in range(len(arr[0])):#len(arr[0])=3 temp = []# 数组的第一维维度for j in range(len(arr)):#len(arr)=4temp.append(arr[j][i])arr2.append(temp)
print(arr2)'''
# 输出结果为:
[[1, 4, 7, 10], [2, 5, 8, 11], [3, 6, 9, 12]]
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21- 第二种列表推导式:(和第一种没啥区别就是看上去更简洁)
# python 列表表达式
# 使用嵌套的列表表达式
arr = [[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9],[10, 11, 12]]
# i 为第二个维度,j 为第一个维度
arr2 = [[arr[j][i] for j in range(len(arr))] for i in range(len(arr[0]))]
print(arr2)
'''
# 输出结果为:
[[1, 4, 7, 10], [2, 5, 8, 11], [3, 6, 9, 12]]
'''- 第三种使用python zip函数
# python zip函数
arr = [[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9],[10, 11, 12]]
# zip(* )在这里是解压的作用
# 将arr 看做是一个打包后的数组
arr2 = zip(* arr)
print(list(arr2))
'''
# 输出结果为:
[(1, 4, 7, 10), (2, 5, 8, 11), (3, 6, 9, 12)]
'''5.第四种使用numpy转置
# 使用numpy转置
import numpy as nparr = [[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9],[10, 11, 12]]
arr = np.array(arr)
# 这里可以三种方法达到转置的目的
# 第一种方法
print(arr.T)
# 第二种方法
print(arr.transpose())
# 第三种方法
print(arr.swapaxes(0, 1))
# 上面三种方法等价
'''
# 三种方法的输出结果均为:
[[ 1 4 7 10][ 2 5 8 11][ 3 6 9 12]]
'''- 言归正传,还是再看输入,第一行输入n,d表示矩阵n行d列,然后下面的几行依次输入矩阵Q,K,V,还是选择列表存储吧(类矩阵惯用二维列表表示)。直接用列表推导式。接着就是运算了,这道题其实只用按照逆矩阵的顺序做点乘即可,就是 W(i) 为向量 W 的第 i 个元素,即将 (Q×KT) 第 i 行中的每个元素都与 W(i) 相乘。
- 上代码!!!
n, d = map(int, input().split())
Q = [[i for i in map(int, input().split())] for j in range(n)]
K = [[i for i in map(int, input().split())] for j in range(n)]
V = [[i for i in map(int, input().split())] for j in range(n)]
W = [i for i in map(int, input().split())]
tmp = []#存放 计算: K的转置 * V
ans = []# 计算 Q * tmp = ans# 计算 K的转置 * V = tmp
for i in range(d):tmp.append([])#print(tmp)for j in range(d):tmp[i].append(0)#把每一步的初始计算: K的转置 * V先赋值为0#print(tmp)for k in range(n):#k表示行,注意这里只按照逆矩阵的顺序遍历运算即可n是原矩阵的行tmp[i][j] += K[k][i]*V[k][j]#矩阵的运算相乘再相加#print(tmp)
# 计算 Q * tmp = ans
for i in range(n):ans.append([])for j in range(d):ans[i].append(0)for k in range(d):ans[i][j] += Q[i][k]*tmp[k][j]ans[i][j] *= W[i]for i in range(n):a = []for j in range(d):a.append(ans[i][j])print(*a)#输出的时候空格隔开每一个元素总结

相关文章:

CCF CSP认证 历年题目自练Day35
题目一 试题编号: 202305-1 试题名称: 重复局面 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目背景 国际象棋在对局时,同一局面连续或间断出现3次或3次以上,可由任意一方提出和棋。 问题…...

应用crash时发送广播及信息
一、环境 高通865 Android 10 二、情景 应用崩溃时,将奔溃信息以广播的形式发送 二、代码位置 frameworks/base/core/java/com/android/internal/os/RuntimeInit.java private static class KillApplicationHandler implements Thread.UncaughtExceptionHandle…...

【亲测可用】图像目标识别入门-利用笔记本电脑摄像头识别人脸标记出来采用深度学习模型实现
更高的精度和准确性,可以考虑使用基于深度学习的人脸检测和识别方法,例如基于人脸特征的人脸检测器和具有高识别率的人脸识别模型。下面是使用基于深度学习的人脸检测和识别方法的代码示例: 首先,安装必要的库和模型:…...
数字孪生技术:煤矿运输的未来革命
煤矿是我国能源工业的重要支柱,然而,煤矿运输过程中一直存在着诸多问题,如安全隐患、能源浪费、效率低下等,这不仅对煤矿行业的可持续发展构成威胁,也对环境造成负面影响。因此,数字孪生技术应运而生&#…...
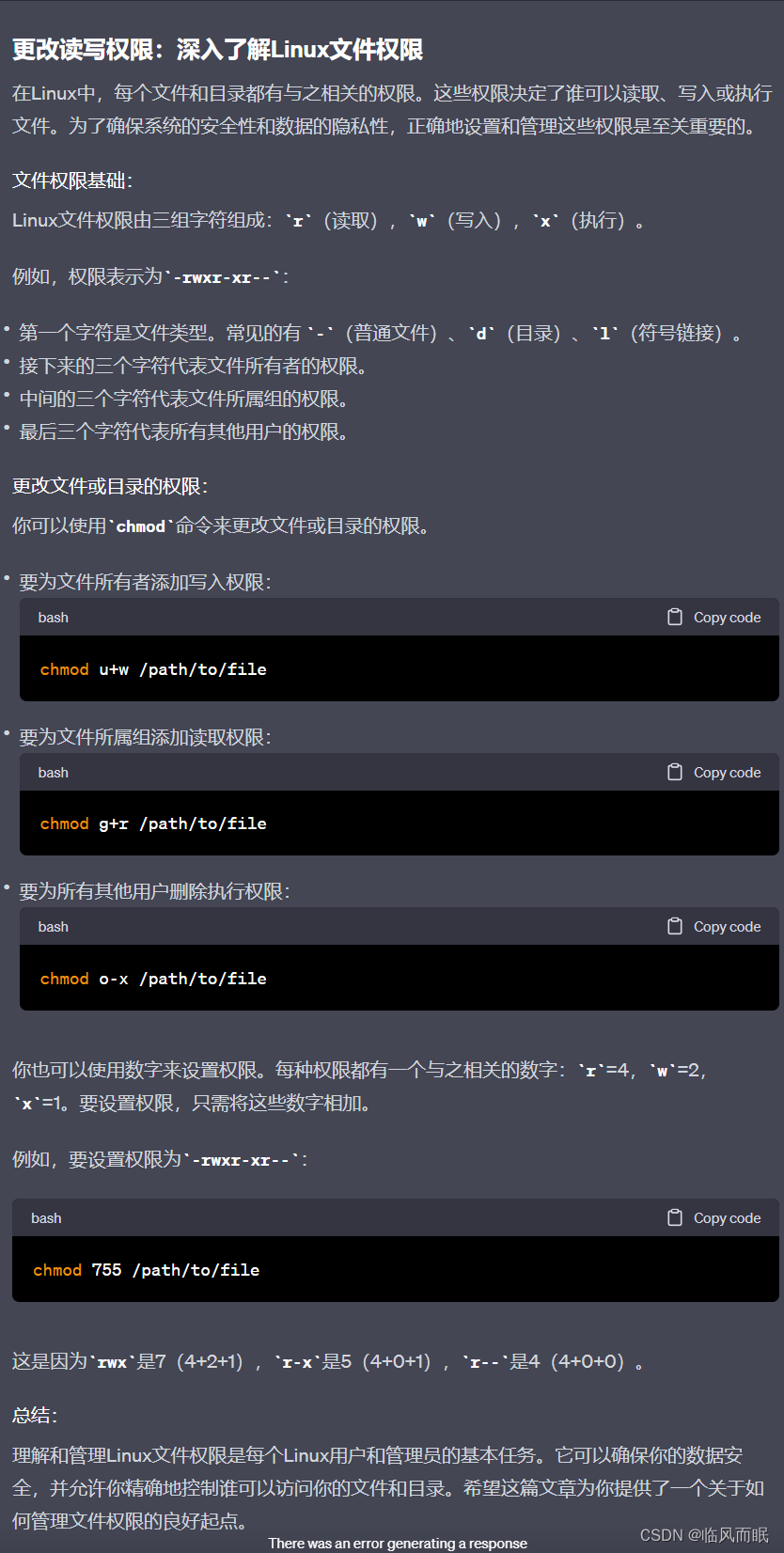
一些bug总结
今天被几个小问题和bug折磨了一天,来总结一下… 权限问题 用vscode连接服务器,如果是在root用户连接的情况下新建的文件/文件夹,然后切换到别的用户的时候去写的代码 可能会遇到各种问题 解决方案是更改文件或文件夹的所有权。这可以通过使用…...

第三章 内存管理 九、基本分段存储管理方式
目录 一、概括 二、什么是分段 三、段表 四、地址转换 五、分段和分页的对比 六、总结 一、概括 基本分段存储管理方式是一种操作系统的内存管理方式,采用这种方式,将进程所需的内存分成若干个段,每个段都可以单独进行管理和保护。 具…...

轻重链剖分+启发式合并专题
Codeforces-741D(Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths) 一棵根为1 的树,每条边上有一个字符(a-v共22种)。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中…...
、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略)
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略 目录 信贷风控简介 信贷风控两大场景...
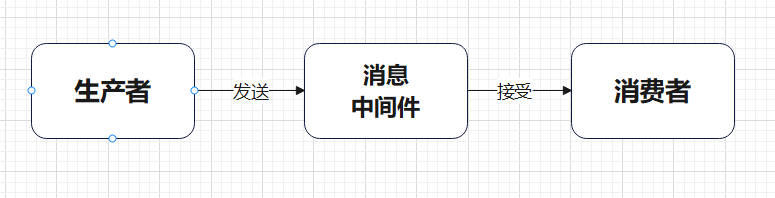
【学习笔记】RabbitMQ01:基础概念认识以及快速部署
参考资料 RabbitMQ官方网站RabbitMQ官方文档噼咔噼咔-动力节点教程 文章目录 一、认识RabbitMQ1.1 消息中间件(MQ Message Queue 消息队列1.2 主流的消息中间件1.3 MQ的应用场景1.3.1 异步处理1.3.2 系统解耦1.3.3 流量削峰1.3.4 日志处理 二、RabbitMQ运行环境搭建…...

Java数据结构之第二十章、手撕平衡AVL树
目录 一、二叉平衡树 1.1二叉搜索树回顾以及性能分析 1.1.1二叉搜索树的概念 1.2二叉搜索树的查找 1.3二叉树查询性能分析 二、AVL树 2.1AVL树的概念 2.2AVL树节点的定义 2.3AVL树的插入 2.4AVL树的旋转 2.4.1新节点插入较高左子树的左侧---右单旋 2.4.2新节点插入较…...

SQL 在PostgreSQL中使用SQL将多行连接成数组
在本文中,我们将介绍如何使用SQL语言在PostgreSQL数据库中将多行数据连接成一个数组。在开发和分析应用程序时,我们经常需要将数据库中的多个行合并为一个,以便更方便地进行处理和分析。PostgreSQL提供了一种名为ARRAY_AGG的聚合函数…...

Ajax技术实现前端开发
一、原生AJAX 1.1AJAX 简介 AJAX 全称为Asynchronous JavaScript And XML,就是异步的JS 和XML。 通过AJAX 可以在浏览器中向服务器发送异步请求,最大的优势:无刷新获取数据。 AJAX 不是新的编程语言,而是一种将现有的标准组合在一起使用的新方式。 1.2XML 简介 XML 可扩…...

WebMail:网页注册成功发送邮件
1.特别注意 isELIgnored"false" 如果没有这个El表达式无法识别 2.pre work pox.xml <dependencies><dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>3.8.1</version><scope>…...
Electron之集成vue+vite开发桌面程序
在electron中集成vue开发桌面程序 使用我们之前创建的electron项目 创建vue 项目 命令行进入electron根目录 执行下面命令 npm create vitelatest vue -- --template vue这样就创建了一个vue项目,文件名是vue,命令行进入vue下,执行下面命…...

pycharm社区版创建Django项目的一种方式
pycharm社区版创建Django项目 pycharm创建New project安装django,如果安装过可略过安装完成后查看安装情况生成Django项目需要的文件这里注意生成语句后面的 . 不可以省略 生成文件后,框架搭建完成,配置启动我这里在配置完后,报了…...
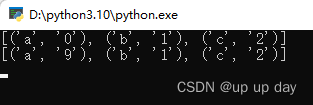
Python configparser模块使用教程
文章目录 .ini 拓展名文件简介.ini 文件格式1. 节2. 参数3. 注解 configparser 模块简介configparser 模块的初始化和读取获取 ini 中所有 section获取 section 下的 key获取 section 下的 value获取指点section的所用配置信息修改某个key,如果不存在则会出创建检查…...

Kotlin + 协程 + Room 结合使用
文章目录 前言集成Room结合协程的使用总结 一、前言, 现在kotlin 是趋势,那必然就要用到协程,还有就是随着jetpack 的发力,带来了很多好用的库,比如今天提到Room,是一个类似greenDao的数据库。它不但支持kotlin协程…...
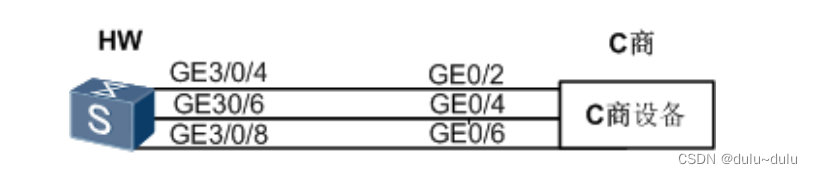
网工记背命令(6)----链路聚合配置
目录 1.配置手工负载分担模式链路聚合 2.配置LACP模式的链路聚合 3.HUAWEI设备与C厂商设备对接 链路聚合(Link Aggregation)是将多条物理链路捆绑在一起成为一条逻辑链路,从而增加链路带 宽的技术。 常用配置命令 1、执行命令 interface …...

使用 Service 把前端连接到后端
使用 Service 把前端连接到后端 如何创建前端(Frontend)微服务和后端(Backend)微服务。后端微服务是一个 hello 欢迎程序。 前端通过 nginx 和一个 Kubernetes 服务暴露后端所提供的服务。 使用部署对象(Deployment ob…...

vue 如何优化首页的加载速度?vue 首页白屏是什么问题引起的?如何解决呢?
vue 如何优化首页的加载速度? 路由懒加载ui框架按需加载gzip压缩 vue首页白屏是什么问题引起的 第一种,打包后文件引用路径不对,导致找不到文件报错白屏 解决办法:修改一下config下面的index.js中bulid模块导出的路径。因为in…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
