联合体(共用体)
1. 联合类型的定义
2.联合大小的计算
#include<stdio.h>
union un1
{int a;char b;
};
union un2
{char str[5];int c;
};
void main()
{union un1 u1;union un2 u2;u1.a =0x11223344;//u1.b = 0x55;printf("%d\n",sizeof(union un1));printf("%d\n", sizeof(union un2));printf("%x\n",u1.a);//printf("%x\n", u1.b);
}
因为u1中数据类型最大的占4个字节,所以u1大小为4字节。因为u2中有一个字符串数组,最大为5字节,但是对齐的话得对齐最大数据类型的整数倍。也就是8。
相关文章:

联合体(共用体)
1. 联合类型的定义 联合也是一种特殊的自定义类型。 这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间。 2.联合大小的计算 联合的大小 至少是最大成员的大小 。 当最大成员大小不是最大对齐数的整数倍的时候,就要对 齐到最大对齐数…...

从零开始:GitFlow详细教程,轻松掌握分支策略
前序 GitFlow是一种用于管理Git仓库中软件开发工作流程的模型,它提供了一种结构化的方法来处理特性开发、版本发布和维护。下面是一个详细的GitFlow教程,帮助你了解GitFlow的基本概念和使用方法。 安装GitFlow 首先,确保你已经安装了Git。…...

深度学习硬件介绍
目录 1. 深度学习电脑选型1.1 深度学习常用框架1.2 深度学习硬件选择1.3 GPU 厂商介绍科普 你真的需要这么一块阵列卡 1. 深度学习电脑选型 1.1 深度学习常用框架 常见的深度学习框架:百度的飞桨框架、Google 的TensorFlow,伯克利亚学院的Caffe&#x…...
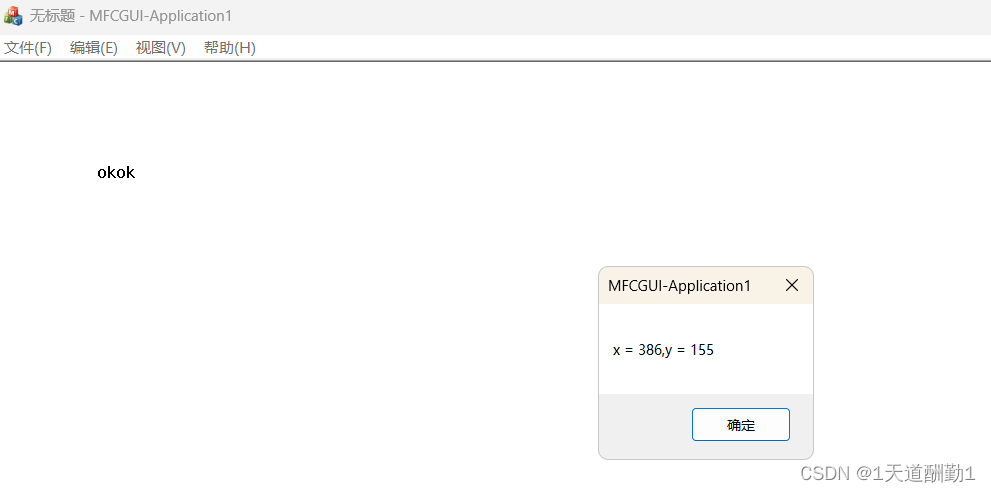
利用向导创建MFC
目录 1、项目的创建: 2、项目的管理 : 3、分析以及生成的项目代码 : (1)、查看CFrame中的消息映射宏 (2)、自动生成事件 (3)、在CFrame中添加对应的鼠标处理函数 …...
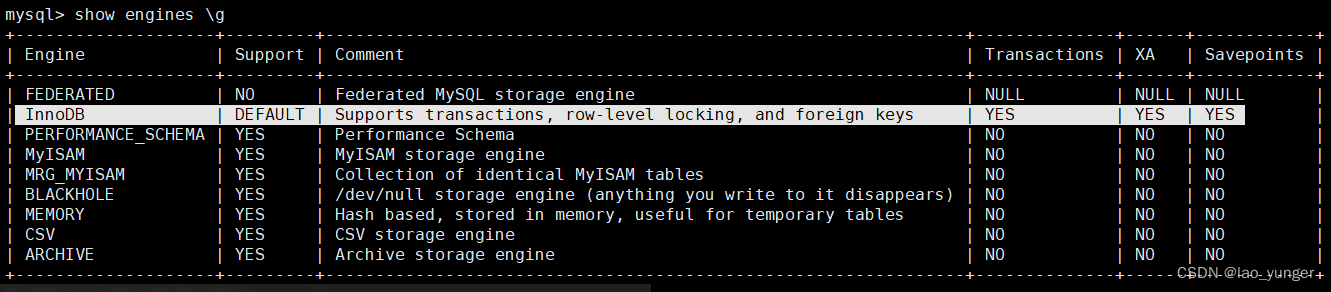
MySQL 8.0 OCP认证精讲视频、环境和题库之五 事务、缓存
redo log buffer: 缓存与事务有关的redo log ,用来对mysql进行crash恢复,不可禁用; 日志缓冲区是存储要写入磁盘上日志文件的数据的内存区域。日志缓冲区大小由innodb_Log_buffer_size变量定义。 默认大小为16MB。日志缓冲区的内容会定…...
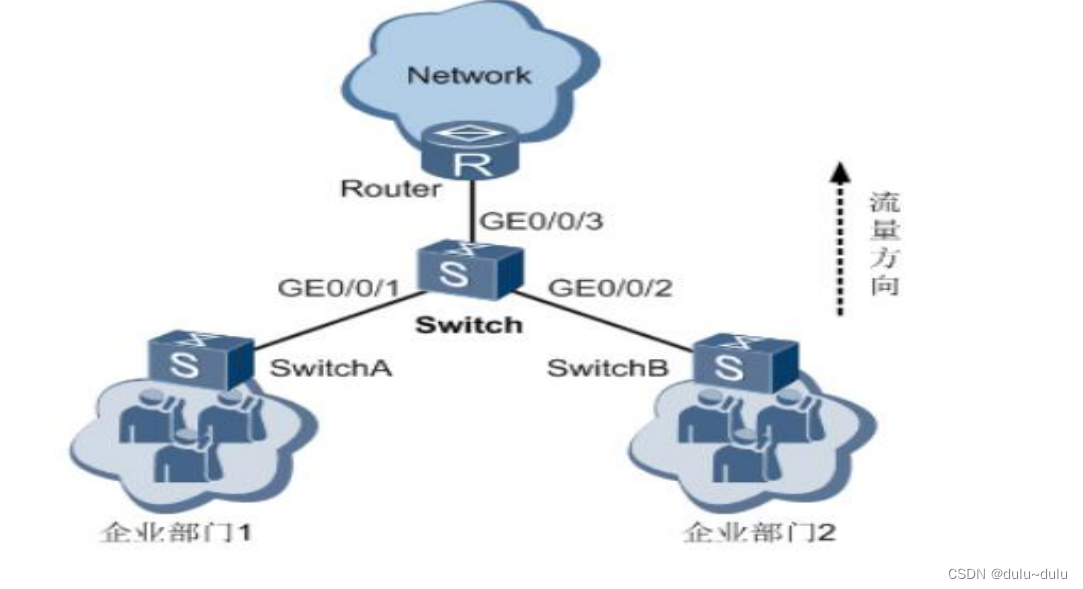
ACL配置
目录 1.使用基本ACL配置交换telnet访问的权限 2.使用高级ACL配置流分类实现限制互访某一台服务器 3.使用二层ACL配置流分类拒绝指定报文通过 4.通过流策略实现策略路由(重定向到不同的下一跳) 5.通过流策略实现不同网段间限制互访 6.通过流策略实现限速功能 7.通过流策略…...

微信小程序修改van-popup的背景颜色
效果图: van-popup背景颜色渐变 使用深度修改样式不生效,直接在 custom-style里面修改即可; <van-popup position"bottom"custom-style"height:25%;background:linear-gradient(95deg, #F8FCFF -0.03%, #EDF5FF 64.44…...
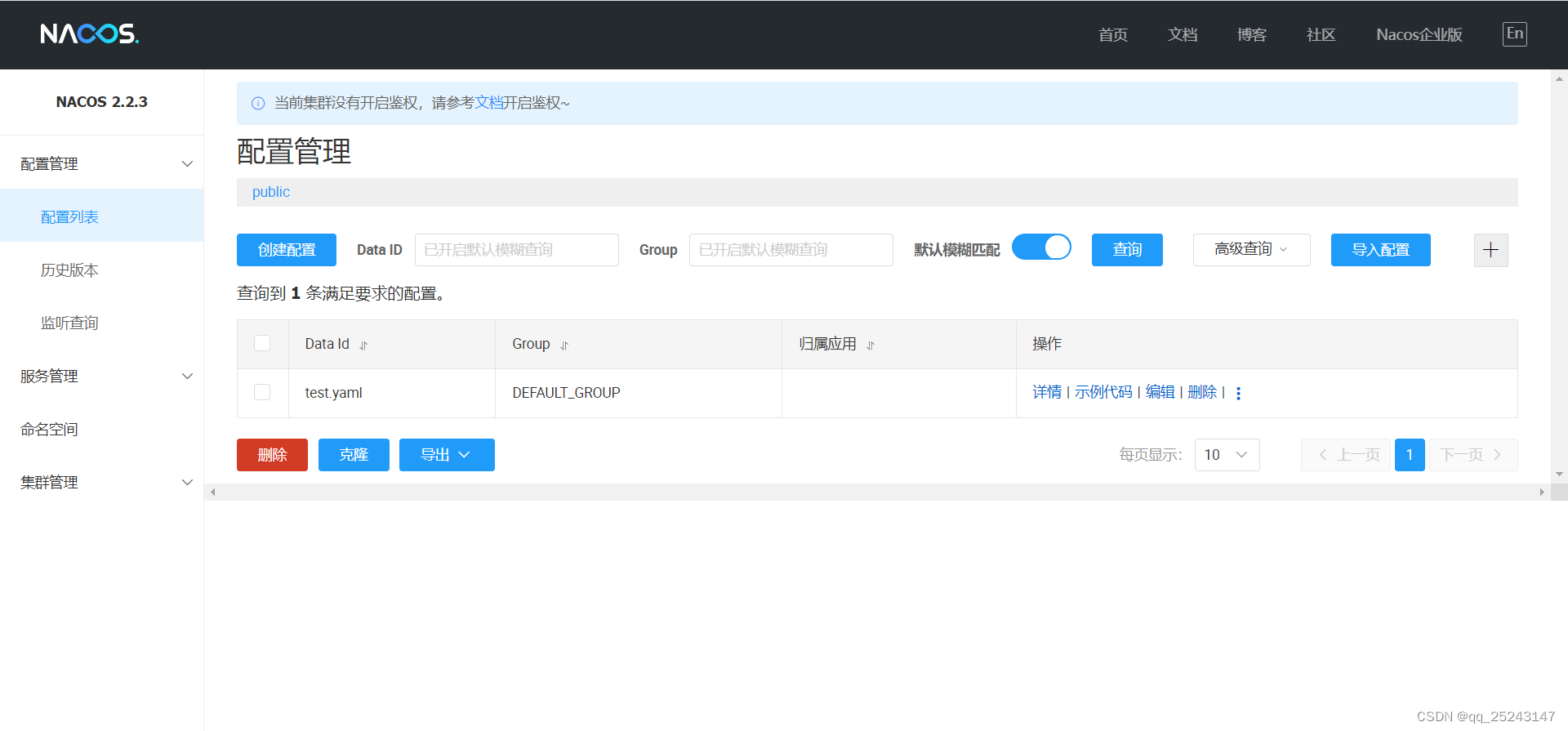
SpringCloud-Nacos
一、介绍 (1)作为服务注册中心和配置中心 (2)等价于:EurekaConfigBus (3)nacos集成了ribbon,支持负载均衡 二、安装 (1)官网 (2) …...
)
动态规划12(Leetcode221最大正方形)
代码: class Solution {public int maximalSquare(char[][] matrix) {int m matrix.length;int n matrix[0].length;int[][]area new int[m][n];area[0][0] matrix[0][0];int max 0;for(int i0;i<m;i){area[i][0] matrix[i][0]1? 1:0;max Math.max(area…...
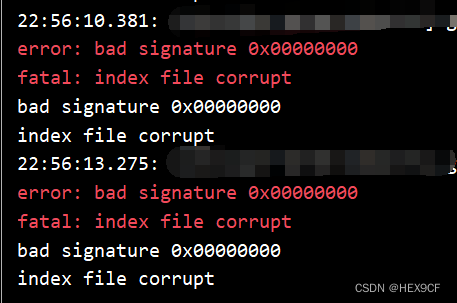
【Git】bad signature 0x00000000 index file corrupt. fatal: index file corrupt
问题描述 电脑写代码时蓝屏。重启后 git commit 出错。 error: bad signature 0x00000000 fatal: index file corrupt原因分析 当电脑发生蓝屏或异常关机时,Git 的索引文件可能损坏。 解决方案 删除损坏的索引文件。 rm -Force .git/index回退到上一个可用的版…...

GO 语言的函数??
函数是什么? 学过编程的 xdm 对于函数自然不会陌生,那么函数是什么呢? 函数是一段可以重用的代码块,可以被多次调用,我们可以通过使用函数,提高咱们代码代码的模块化,提高程序的可读性和可维护…...
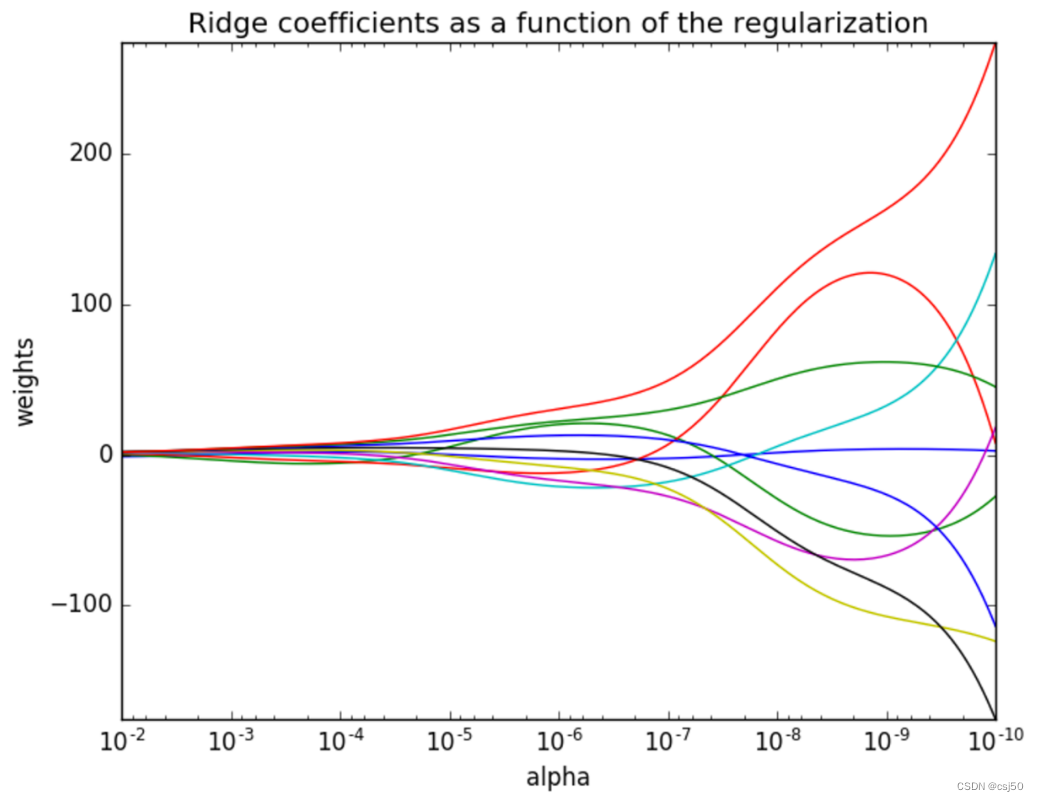
机器学习基础之《回归与聚类算法(3)—线性回归优化:岭回归》
一、什么是岭回归 其实岭回归就是带L2正则化的线性回归 岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果 二、API 1、sklearn.linear_model.Ridge(alpha1.0, fit_interceptTrue…...
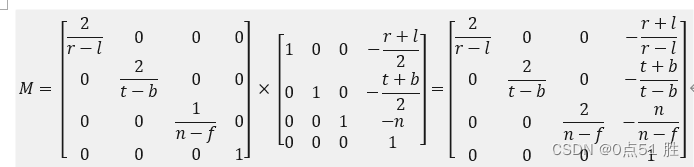
DirectX3D 正交投影学习记录
所谓正交投影变换,就是已知盒状可视空间内任意点坐标(x,y,z),求解垂直投影到xy平面的对应点坐标。 按照这个定义,xyz坐标系本身就是正交坐标系,盒状可视空间内任意点的坐标(x,y,z)投影到(x,y)平面,只要简单地丢弃z坐标…...
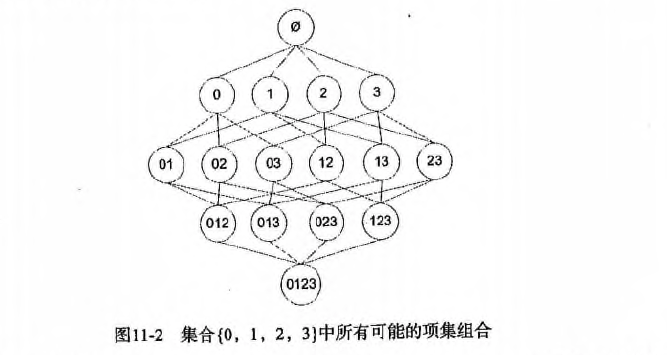
数据挖掘十大算法--Apriori算法
一、Apriori 算法概述 Apriori 算法是一种用于关联规则挖掘的经典算法。它用于在大规模数据集中发现频繁项集,进而生成关联规则。关联规则揭示了数据集中项之间的关联关系,常被用于市场篮分析、推荐系统等应用。 以下是 Apriori 算法的基本概述&#x…...

[蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11, 最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N, M和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 输入 #1 3…...

解决在部署springboot项目的docker中执行备份与之相连接的mysql容器命令
文章目录 问题描述解决思路问题解决容器构建mysql客户端安装容器与主机的交互docker中执行 mysqldump 命令解决mysql8密码验证问题解决密码插件警告 问题描述 由于,使用1panel可视化的面板来部署springboot项目,可以很方便地安装和使用mysql,…...

正文Delphi XE Android下让TMemo不自动弹出键盘
用TMemo来显示一段说明文字,可一点Memo,就弹出键盘,找了半天控制键盘的属性,没找到。最后将readOnly设置为True搞定。 如果需要一个form都不显示keyboard,那么可以利用全局变量 VKAutoShowMode来控制,这个全局变量可以有下面三个值…...

[1Panel]开源,现代化,新一代的 Linux 服务器运维管理面板
测评介绍 本期测评试用一下1Panel这款面板。1Panel是国内飞致云旗下开源产品。整个界面简洁清爽,后端使用GO开发,前端使用VUE的Element-Plus作为UI框架,整个面板的管理都是基于docker的,想法很先进。官方还提供了视频的使用教程&…...
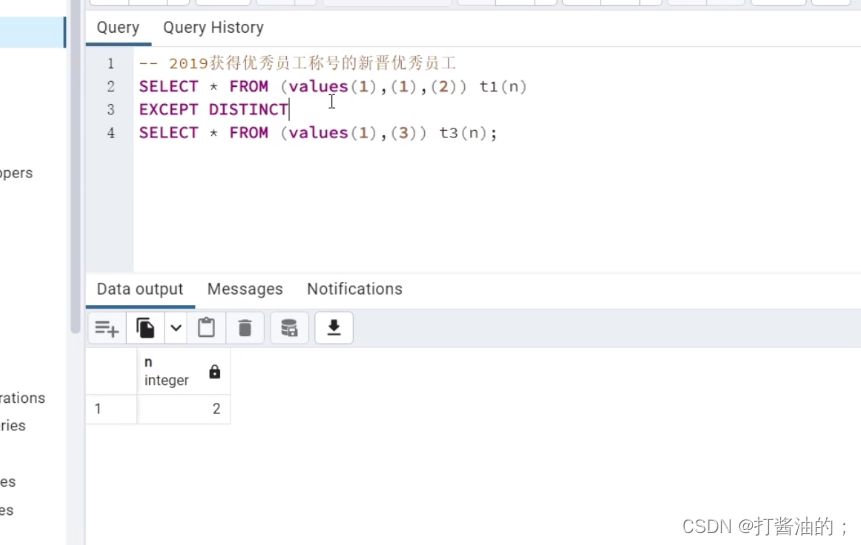
PG集合查询
1.运算符 1.1 union并集 连接上下语句 union distinct连接并且去重 all不去重 1.2 intersect交集 上下交集 distinct连接并且去重 all不去重 1.3 except除外 上面除了下面 distinc去重 all不去重...
目标检测应用场景和发展趋势
参考: 目标检测的未来是什么? - 知乎 (zhihu.com)https://www.zhihu.com/question/394900756/answer/32489649815大应用场景 1 行人检测: 遮挡问题:行人之间的互动和遮挡是非常常见的,这给行人检测带来了挑战。非刚性…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...

android计算器代码
本次作业要求实现一个计算器应用的基础框架。以下是布局文件的核心代码: <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"andr…...
