当前位置： 首页 > news >正文

【Python机器学习】零基础掌握MinCovDet协方差估计

news 2026/4/2 18:45:29

如何更精准地评估资产的风险和收益？

在投资领域，资产的风险和收益评估是至关重要的。传统的协方差矩阵虽然在某种程度上能反映资产间的关联性，但也存在一定的局限性。例如如果样本数量较少，传统的协方差矩阵可能会出现偏差，从而影响投资决策。

假设现在有一个投资组合，包括4种不同的资产，以下是过去一段时间内这4种资产的收益率：

资产A资产B资产C资产D
5%7%6%4%
4%6%7%5%
6%8%5%7%
…………

为了更精准地评估各资产之间的关联性和风险，可以使用LedoitWolf算法进行更精准的协方差矩阵估计。

文章目录

  • LedoitWolf
    • Sklearn 实现代码演示
    • Sklearn API参数详解与调参
  • 应用案例
    • 三大历史人物对古代市场的影响力分析
    • 高考科目选择优化方案
  • <

相关文章：

【Python机器学习】零基础掌握MinCovDet协方差估计

如何更精准地评估资产的风险和收益？ 在投资领域，资产的风险和收益评估是至关重要的。传统的协方差矩阵虽然在某种程度上能反映资产间的关联性，但也存在一定的局限性。例如如果样本数量较少，传统的协方差矩阵可能会出现偏差，从而影响投资决策。 假设现在有一个投资组合，…...

编程日记 2023/10/19 9:48:27

2023年【四川省安全员A证】模拟试题及四川省安全员A证作业模拟考试

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 2023年四川省安全员A证模拟试题为正在备考四川省安全员A证操作证的学员准备的理论考试专题&#xff0c;每个月更新的四川省安全员A证作业模拟考试祝您顺利通过四川省安全员A证考试。 1、【多选题】36V照明适用的场所条…...

编程日记 2023/10/19 9:47:27

Flask项目log的集成

一、引入log 在项目的init.py文件中&#xff1a; import logging from logging.handlers import RotatingFileHandlerfrom flask_wtf.csrf import CSRFProtect from flask import Flask from flask_sqlalchemy import SQLAlchemy from redis import StrictRedis from flask_s…...

编程日记 2023/10/19 9:46:25

Open3D(C++) 最小二乘拟合平面（拉格朗日乘子法）

目录 一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创，原文链接。 一、算法原理 设拟合出的平面方程为： a x + b y + c...

编程日记 2023/10/19 9:44:24

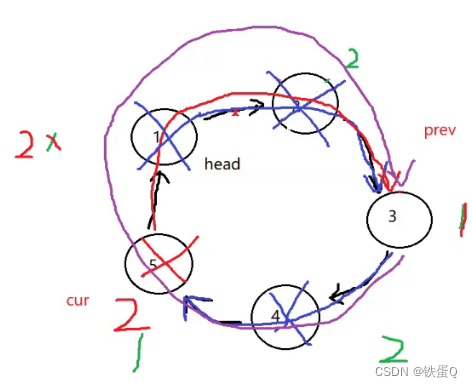
c语言练习93：环形链表的约瑟夫问题

环形链表的约瑟夫问题 环形链表的约瑟夫问题_牛客题霸_牛客网 描述 编号为 1 到 n 的 n 个人围成一圈。从编号为 1 的人开始报数&#xff0c;报到 m 的人离开。 下一个人继续从 1 开始报数。 n-1 轮结束以后&#xff0c;只剩下一个人&#xff0c;问最后留下的这个人编号是…...

编程日记 2023/10/19 9:42:22

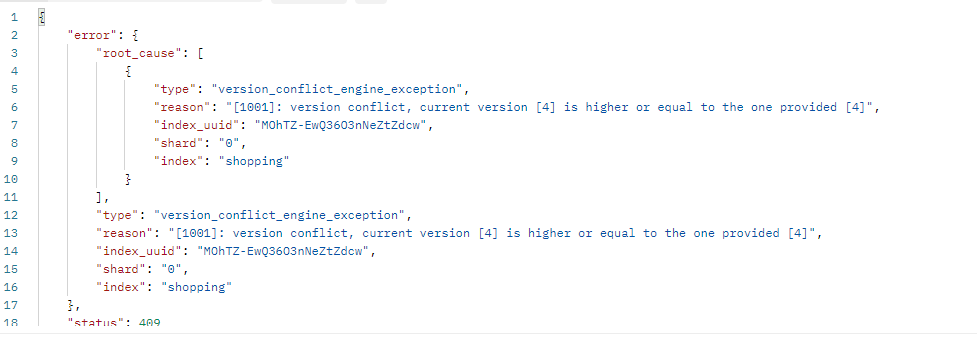
从入门到进阶 之 ElasticSearch 文档、分词器 进阶篇

&#x1f339; 以上分享 ElasticSearch 文档、分词器 进阶篇&#xff0c;如有问题请指教写。&#x1f339;&#x1f339; 如你对技术也感兴趣&#xff0c;欢迎交流。&#x1f339;&#x1f339;&#x1f339; 如有需要&#xff0c;请&#x1f44d;点赞&#x1f496;收藏&#…...

编程日记 2023/10/19 9:41:20

亚马逊云科技多项新功能与服务，助力各种规模的组织拥抱生成式 AI

从初创企业到大型企业&#xff0c;各种规模的组织都纷纷开始接触生成式 AI 技术。这些企业希望充分利用生成式 AI&#xff0c;将自身在测试版、原型设计以及演示版中的畅想带到现实场景中&#xff0c;实现生产力的大幅提升并大力进行创新。但是&#xff0c;组织要怎样才能在企业…...

编程日记 2023/10/19 9:40:18

网站布局都有哪些？

网站布局是指网页中各元素的布局方式&#xff0c;以下是一些常见的网站布局&#xff1a; 栅格布局&#xff1a;将页面分成一个个小格子&#xff0c;再把内容放到对应的格子中。这种布局有利于提高网页的视觉一致性和用户体验&#xff0c;是网站设计中最常用的布局方式之一。流…...

编程日记 2023/10/19 9:39:17

第17章 MQ（一）

17.1 谈谈你对MQ的理解 难度：★ 重点：★★ 白话解析 MQ也要有一跟主线，先理解它是什么，从三个方面去理解就好了：1、概念；2、核心功能；3、分类。 1、概念：MQ（Message Queue），消息队列，是基础数据结构中“先进先出”的一种数据结构。指把要传输的数据（消息）放在队…...

编程日记 2023/10/19 9:38:16

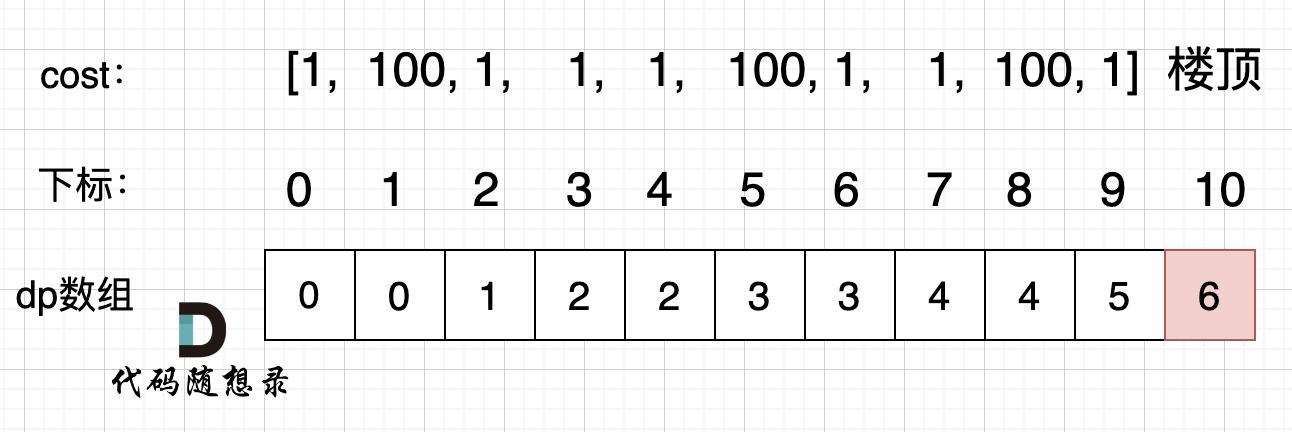
LeetCode算法刷题(python) Day41｜09动态规划｜理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯

目录 动规五部曲LeetCode 509. 斐波那契数LeetCode 70. 爬楼梯LeetCode 746. 使用最小花费爬楼梯 动规五部曲 确定dp数组以及下标的含义确定递归公式dp数组如何初始化确定遍历顺序举例推导dp数组 LeetCode 509. 斐波那契数 力扣题目链接 本题最直观是用递归方法 class Sol…...

编程日记 2023/10/19 9:37:15

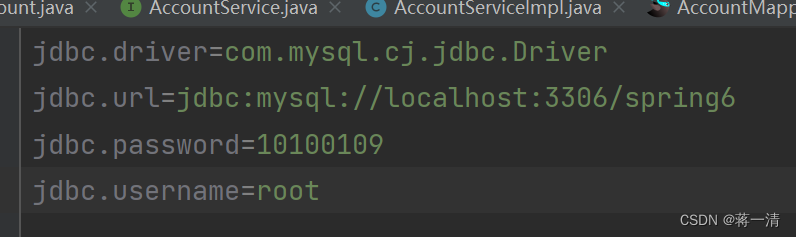
Spring(四)

1、Spring6整合JUnit 1、JUnit4 User类: package com.songzhishu.spring.bean;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component;/*** BelongsProject: Spring6* BelongsPackage: com.songzhishu.spring.bean*…...

编程日记 2023/10/19 9:36:14

2023-10-8讯飞大模型部署2024秋招后端一面（附详解）

1 mybatis的mapper是什么东西 在MyBatis中&#xff0c;mapper是一个核心概念&#xff0c;它起到了桥梁的作用&#xff0c;连接Java对象和数据库之间的数据。具体来说&#xff0c;mapper可以分为以下两个部分&#xff1a; Mapper XML文件&#xff1a; 这是一个XML文件&#xff…...

编程日记 2023/10/19 9:35:13

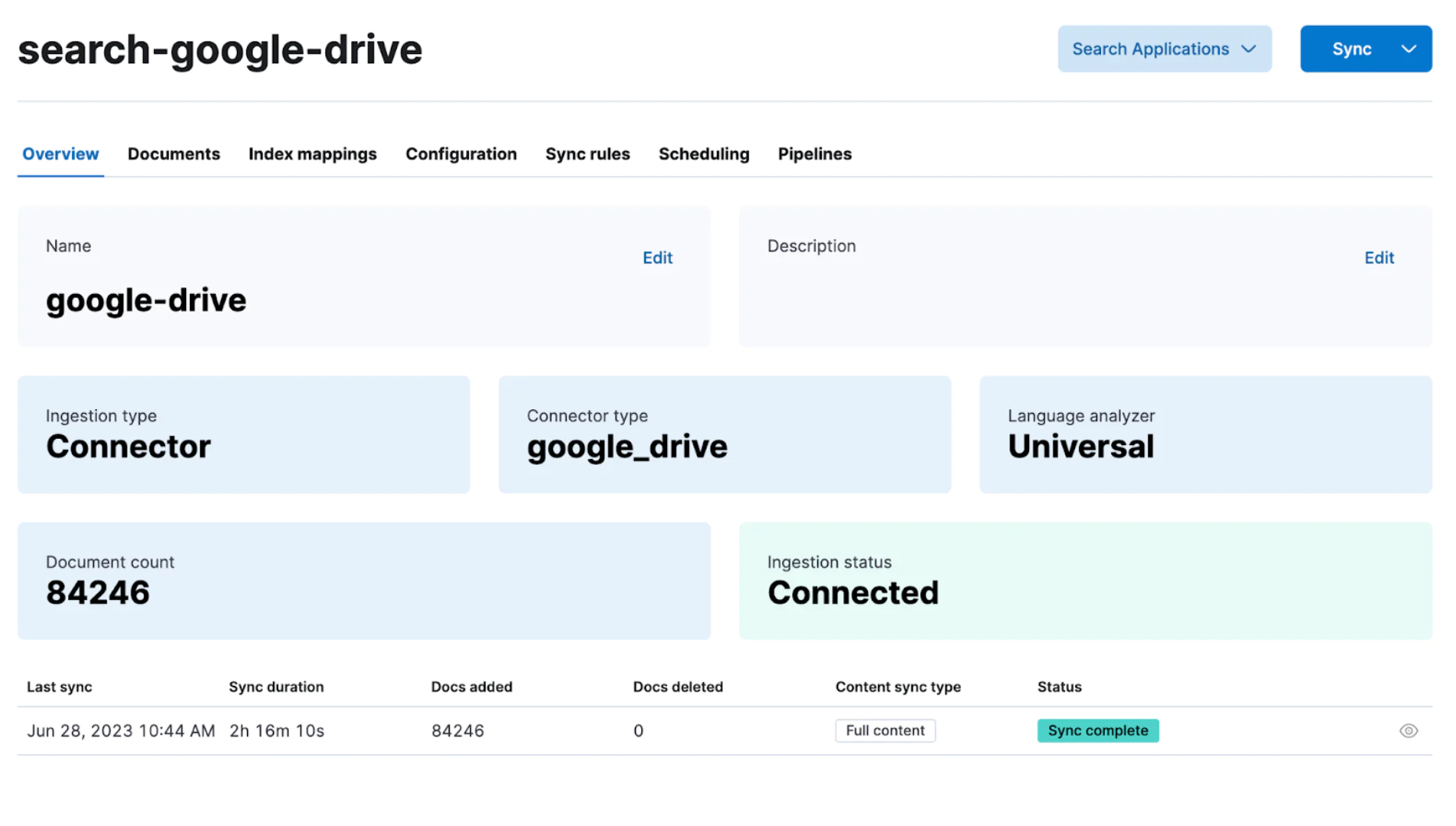
如何为 Elasticsearch 创建自定义连接器

了解如何为 Elasticsearch 创建自定义连接器以简化数据摄取过程。 作者&#xff1a;JEDR BLASZYK Elasticsearch 拥有一个摄取工具库&#xff0c;可以从多个来源获取数据。 但是&#xff0c;有时你的数据源可能与 Elastic 现有的提取工具不兼容。 在这种情况下&#xff0c;你可…...

编程日记 2023/10/19 9:34:11

Debian11 安装 OpenJDK8

1. 下载安装包 wget http://snapshot.debian.org/archive/debian-security/20220210T090326Z/pool/updates/main/o/openjdk-8/openjdk-8-jdk_8u322-b06-1~deb9u1_amd64.deb wget http://snapshot.debian.org/archive/debian-security/20220210T090326Z/pool/updates/main/o/op…...

编程日记 2023/10/19 9:32:09

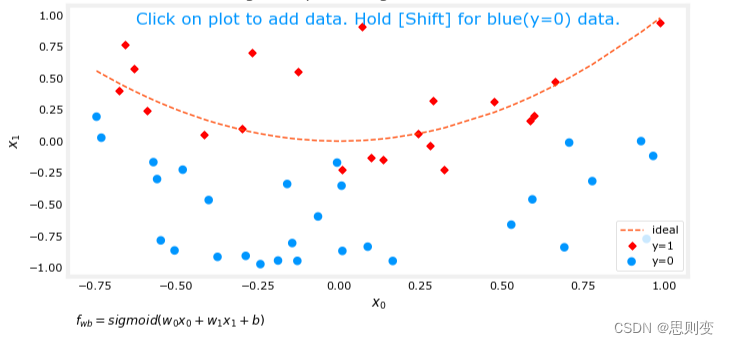
[Machine Learning][Part 6]Cost Function代价函数和梯度正则化

目录 拟合 欠拟合 过拟合 正确的拟合 解决过拟合的方法&#xff1a;正则化 线性回归模型和逻辑回归模型都存在欠拟合和过拟合的情况。 拟合 来自百度的解释&#xff1a; 数据拟合又称曲线拟合&#xff0c;俗称拉曲线&#xff0c;是一种把现有数据透过数学方法来代入一条…...

编程日记 2023/10/19 9:29:07

工业自动化编程与数字图像处理技术

工业自动化编程与数字图像处理技术 编程是计算机领域的基础技能&#xff0c;对于从事软件开发和工程的人来说至关重要。在工业自动化领域&#xff0c;C/C仍然是主流的编程语言&#xff0c;特别是用于工业界面(GUI)编程。工业界面是供车间操作员使用的&#xff0c;使用诸如Hal…...

编程日记 2023/10/19 9:28:06

JY61P.C

/** File Name : JY61P.cDescription : attention © Copyright (c) 2020 STMicroelectronics. All rights reserved.This software component is licensed by ST under Ultimate Liberty licenseSLA0044, the “License”; You may not use this file except in complian…...

编程日记 2023/10/19 9:27:05

Go编程：使用 Colly 库下载Reddit网站的图像

概述 Reddit是一个社交新闻网站&#xff0c;用户可以发布各种主题的内容&#xff0c;包括图片。本文将介绍如何使用Go语言和Colly库编写一个简单的爬虫程序&#xff0c;从Reddit网站上下载指定主题的图片&#xff0c;并保存到本地文件夹中。为了避免被目标网站反爬&#xff0c…...

编程日记 2023/10/19 9:26:04

高性能日志脱敏组件：已支持 log4j2 和 logback 插件

项目介绍 日志脱敏是常见的安全需求。普通的基于工具类方法的方式&#xff0c;对代码的入侵性太强&#xff0c;编写起来又特别麻烦。 sensitive提供基于注解的方式&#xff0c;并且内置了常见的脱敏方式&#xff0c;便于开发。 同时支持 logback 和 log4j2 等常见的日志脱敏…...

编程日记 2023/10/19 9:25:02

一文读懂PostgreSQL中的索引

前言 索引是加速搜索引擎检索数据的一种特殊表查询。简单地说&#xff0c;索引是一个指向表中数据的指针。一个数据库中的索引与一本书的索引目录是非常相似的。 拿汉语字典的目录页&#xff08;索引&#xff09;打比方&#xff0c;我们可以按拼音、笔画、偏旁部首等排序的目录…...

编程日记 2023/10/19 9:24:01

SecGPT-14B完整指南：从镜像拉取、服务启动、参数调优到故障排查

SecGPT-14B完整指南&#xff1a;从镜像拉取、服务启动、参数调优到故障排查 1. SecGPT-14B简介 SecGPT-14B是一款专注于网络安全领域的文本生成模型&#xff0c;基于Qwen2ForCausalLM架构开发&#xff0c;拥有140亿参数规模。该模型专为安全专业人员设计&#xff0c;能够提供…...

编程新知 2026/4/2 18:24:29

Python量化交易系统：专业回测与组合优化

先把最重要的前提说清楚&#xff1a;国内禁止未经许可的程序化自动交易&#xff0c;下面只做量化研究、回测、信号分析&#xff0c;不含实盘自动下单这套是专业完整版量化系统&#xff0c;Python 可直接运行&#xff0c;结构完整、可扩展包含你要的所有高级功能&#xff1a;多股…...

编程新知 2026/4/2 18:01:57

GanttProject：免费开源甘特图工具如何重塑项目管理流程

GanttProject&#xff1a;免费开源甘特图工具如何重塑项目管理流程 【免费下载链接】ganttproject Official GanttProject repository 项目地址: https://gitcode.com/gh_mirrors/ga/ganttproject 在项目管理工具层出不穷的今天&#xff0c;GanttProject以其完全免费开源…...

编程新知 2026/4/2 17:13:08

阿里云物联网平台OTA升级避坑指南：从版本号上报到Bin文件拉取的全流程排错

阿里云物联网平台OTA升级全链路排错实战手册 当设备固件需要远程更新时&#xff0c;OTA技术无疑是救星。但现实往往比理想骨感——版本号莫名失踪、升级包半路"走失"、设备在关键时刻"装聋作哑"。这些问题不仅耽误进度&#xff0c;更可能让生产线停摆。本文…...

编程新知 2026/4/2 16:48:30

TargetMol明星分子—— 2‘,3‘-cGAMP

2,3-cGAMP 是哺乳动物细胞中的内源性 cGAMP。cGAMP 分子属于环状二核苷酸&#xff08;CDNs&#xff09;家族&#xff0c;以三种不同的形式存在&#xff1a;3′3′-cGAMP、2′3′-cGAMP和 3′2′-cGAMP。由哺乳动物细胞中环鸟苷腺苷酸合成酶&#xff08;cyclic guanosine monoph…...

编程新知 2026/4/2 16:15:39

【飞机】倾转旋翼飞机齿轮箱建模与Matlab仿真（含非线性阻尼和立方摩擦效应）

✅作者简介&#xff1a;热爱科研的Matlab仿真开发者&#xff0c;擅长毕业设计辅导、数学建模、数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。&#x1f34e; 往期回顾关注个人主页&#xff1a;Matlab科研工作室&#x1f447; 关注我领取海量matlab电子书和…...

编程新知 2026/4/2 13:34:40

GD32外部晶振配置不当引发串口乱码的时钟树深度解析与修复

1. 时钟树&#xff1a;微控制器的心跳发生器 第一次用GD32调串口的朋友&#xff0c;八成遇到过这样的场景&#xff1a;代码明明和官方例程一模一样&#xff0c;烧录后串口助手却疯狂输出乱码。这种时候千万别急着怀疑人生&#xff0c;问题的根源往往藏在那个不起眼的外部晶振配…...

编程新知 2026/4/2 13:10:23

FadCam 安卓后台视频录制应用，支持屏幕关闭录制，多画质高帧率，隐私保护，适配个人安防与事件记录等正当用途

大家好&#xff0c;我是大飞哥。在个人安防、事件记录、现场取证等场景中&#xff0c;普通安卓录屏应用大多需要保持屏幕常亮&#xff0c;不仅容易暴露录制行为&#xff0c;还会快速消耗电量&#xff0c;无法满足隐蔽、长效录制的需求&#xff0c;而部分后台录制工具又存在隐私…...

编程新知 2026/4/2 12:48:11

Pixiv -直连-手机电脑全平台可用，聚合多个资源一站搞定

功能特点 全平台支持&#xff1a;兼容 Android、iOS、Windows 和 macOS 系统&#xff0c;覆盖主流设备。直连访问&#xff1a;内置优化网络链路&#xff0c;绕过访问限制&#xff0c;无需额外配置或登录即可加载内容。无广告体验&#xff1a;去除官方客户端的广告干扰&#xf…...

编程新知 2026/4/2 11:51:13

javase的第一次博客

1&#xff0c;计算机简介&#xff1a;用于数据计算和处理2&#xff0c;计算机的硬件和软件&#xff1a;计算机硬件&#xff1a;运算器&#xff0c;控制器&#xff0c;存储器&#xff0c;输入设备&#xff0c;输出设备&#xff08;冯 诺依曼模型&#xff09;CPU&#xff1a;运算…...

编程新知 2026/4/2 11:06:26