Apriori(关联规则挖掘算法)
关联规则分析
-
事务库
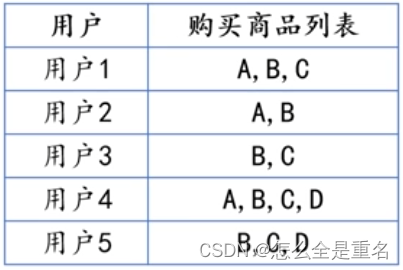
上表所示的购物篮数据即是一个事务库,该事务库记录的是用户行为的数据。 -
事务
上表事务库中的每一条记录被称为一笔事务。在购物篮事务中,每一次购物行为即为一笔事务,例如第一行数据“用户1购买商品A,B,C”即为一条事务。 -
项和项集
在购物篮事务中,每样商品代表一个项,项的集合称为项集。每样商品的组合构成项集,例如“A,B”、 “A,C”、 “B,C”、 “A,B,C”都是一个项集,其实也就是不同商品的组合。 -
关联规则
关联规则是形如X → Y的表达式,X称为前件,Y称为后件。
注意X和Y不是指单一的商品,而是指上面提到的项集,比如其形式可以为:{A, B} →{C},其含义就是如果购买商品A和B的用户也会买C。 -
支持度(Support)
项集的支持度定义为包含该项集的事务在所有事务中所占的比例。 -
频繁项集
支持度大于等于人为设定的阈值(该阈值也称为最小支持度)的项集即为频繁项集,其实也就是指该项集在所有事务中出现的较为频繁。 -
置信度(Confidence)
置信度表示在关联规则的先决条件X发生的条件下,关联结果Y发生的概率
在购物篮事务当中,关联规则X → Y的置信度为购买商品X的基础上购买商品Y的概率P(Y|X),据公式有:
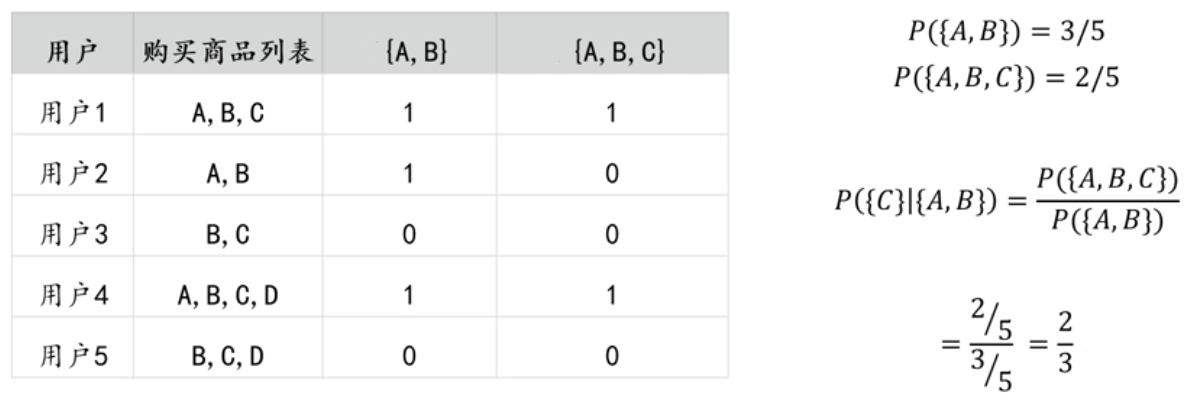
- 强关联规则
寻找强关联规则的主要步骤:
- 先寻找满足最小支持度的频繁项集
- 在频繁项集中寻找到满足最小置信度的关联规则
- 提升度(Lift)
提升度表示先购买X对Y的概率的提升作用,用来判断规则是否有实际价值,即使用规则后商品在购物车中出现的频率是否高于商品单独出现在购物车中的频率。如果大于1说明规则有效,小于1则无效,等于1则表示X与Y相互独立。
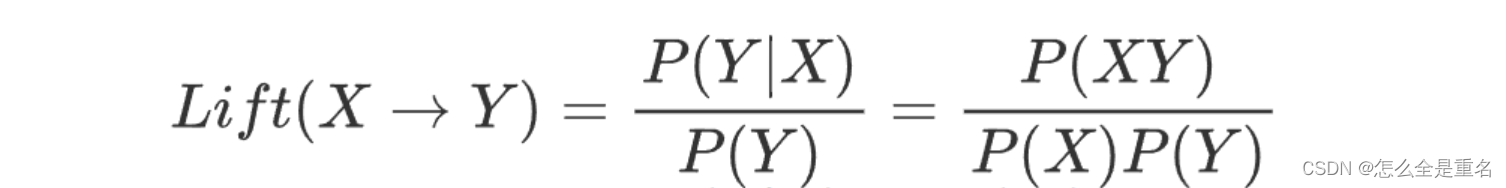
满足最小支持度和最小置信度的规则,叫做“强关联规则”。然而,强关联规则里,又分为有效的强关联规则和无效的强关联规则。具体划分情况如下:
若Lift(X→Y)>1,则规则“X→Y”是有效的强关联规则。
若Lift(X→Y)<1,则规则“X→Y”是无效的强关联规则。
若Lift(X→Y) =1,则表示X与Y相互独立。
注意:
关联规则分析与协同过滤算法都可以用来作为推荐系统的实现,但仍有区别:
- 协同过滤算法是基于用户或商品之间的距离或相似度进行推荐
- 关联规则分析是通过寻找强关联规则后进行推荐
Apriori
Apriori 是一种数据挖掘算法,用于发现数据集中的频繁项集和关联规则。它通常用于市场篮分析,以确定哪些商品通常一起购买。这个算法基于"先验原则",它假设如果一个项集是频繁的,那么它的所有子集也必须是频繁的。这一假设有助于减少搜索空间,提高算法的效率
Apriori算法步骤
- 设定最小支持度和最小置信度
- 根据最小支持度找出所有的频繁项集
- 根据最小置信度发现强关联规则
以购物篮数据演示Apriori算法的计算步骤,数据如下所示:
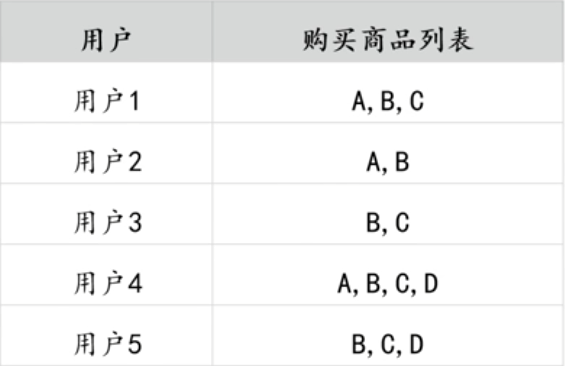
-
设定最小支持度和最小置信度
- 首先设置最小支持度为2/5,也即40%
- 其次设置最小置信度为4/5,也即80%
-
根据最小支持度找出所有的频繁项集
Apriori算法采用了一个精巧的思路来加快运算速度:
先计算长度为1的项集,然后挖掘其中的频繁项集;再将长度为1的频繁项集进行排列组合,从中挖掘长度为2的频繁项集,然后以此推。核心逻辑是一个迭代判断的思想:如果连长度为n-1的项集都不是频繁项集,那就不用考虑长度为n的项集了,例如,如果在迭代的过程发现{A, B, C}不是频繁项集,那么{A, B, C, D}必然不是频繁项集,也就不用去考虑它了。
首先计算长度为1的候选项集,扫描交易数据集,统计每种商品出现的次数,如下表 所示: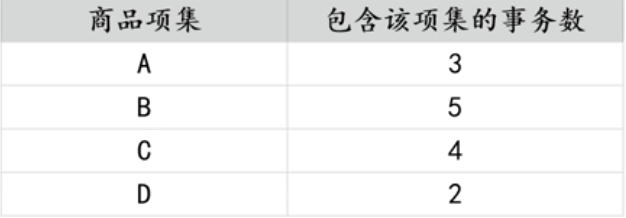
将长度为1的频繁项集进行两两组合,形成长度为2的候选集,扫描交易数据集,统
计各个候选项集在购物篮事务中出现的次数,如下表所示:
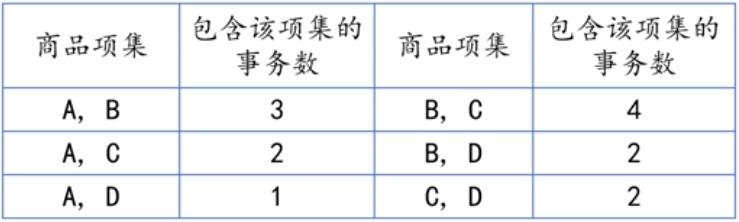
将长度为2的频繁项集进行两两组合,形成长度为3的候选集,扫描交易数据集,统计各个候选项集在购物篮事务中出现的次数,如下表所示:
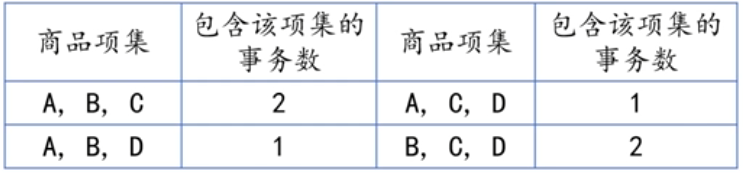
两个数据之间,所以我们需要选择长度大于1的频繁项集,长度大于1的所有频繁项 集,如下表所示:
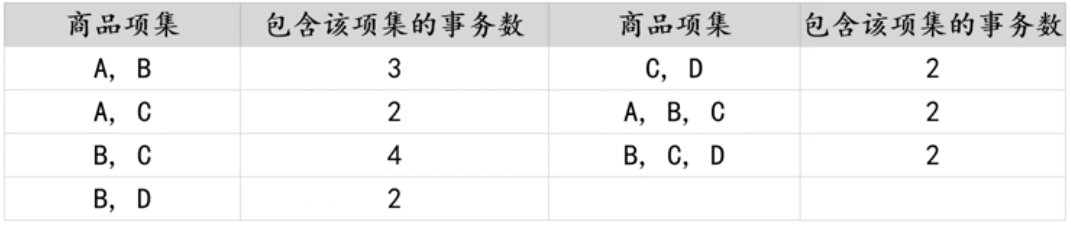
-
根据最小置信度发现强关联规则
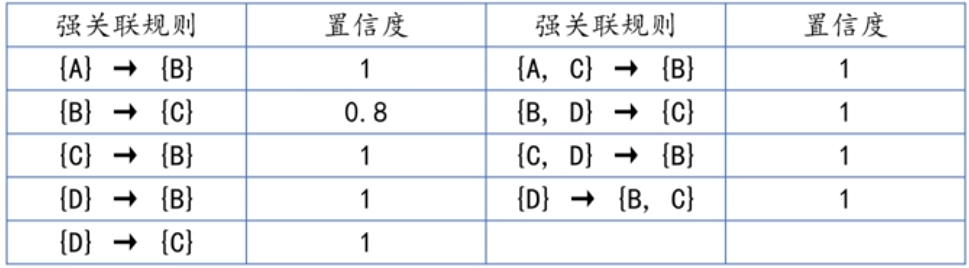
简单代码
transactions = [['A', 'B', 'C'], ['A', 'B'], ['B', 'C'], ['A', 'B', 'C', 'D'], ['B', 'C', 'D']]from apyori import apriori
# 调用apriori函数,指定最小支持度和最小置信度
rules = apriori(transactions, min_support=0.4, min_confidence=0.8)
# 将生成器对象转化成列表
results = list(rules)for i in results: # 遍历results中的每一个频繁项集for j in i.ordered_statistics: # 获取频繁项集中的关联规则X = j.items_base # 关联规则的前件Y = j.items_add # 关联规则的后件x = ', '.join([item for item in X]) # 连接前件中的元素y = ', '.join([item for item in Y]) # 连接后件中的元素if x != '': # 防止出现关联规则前件为空的情况print(x + ' → ' + y) # 通过字符串拼接的方式更好呈现结果
相关文章:

Apriori(关联规则挖掘算法)
关联规则分析 事务库 上表所示的购物篮数据即是一个事务库,该事务库记录的是用户行为的数据。 事务 上表事务库中的每一条记录被称为一笔事务。在购物篮事务中,每一次购物行为即为一笔事务,例如第一行数据“用户1购买商品A,B,C”即为一条事…...

new Object()到底占用几个字节
Java内存模型 对象内存中可以分为三块区域:对象头(Header),实例数据(Instance Data)和对齐填充(Padding),以64位操作系统为例(未开启指针压缩的情况)Java对象布局 如下图所示: 其中对象头中的Mark Word中的详细信息在文章synchr…...

瞬态抑制二极管TVS的工作原理?|深圳比创达电子EMC(上)
TVS二极管具有响应速度快、漏电流小、钳位电压稳以及无寿命衰减的特性,从小到信号线静电防护,大到电力系统抗雷击浪涌,TVS都发挥着至关重要的作用。本章对瞬态抑制二极管TVS工作机理展开分析,供产品选型参考。接下来就跟着深圳比创…...

Nginx 同一端口 同时支持http与https 协议
文章目录 需求分析 需求 通过 nginx ,让同一端口 同时支持http与https 协议 分析 通过使用 Nginx,可以实现同一端口同时支持 HTTP 和 HTTPS 协议。下面是一种可能的配置方式: 配置 HTTP 服务 在 Nginx 配置文件中,添加以下配置…...

【Express】文件上传管理 multer 中间件
Multer是Node.js中用于处理文件上传的中间件。它可以帮助你处理文件上传的相关逻辑,如接收和保存上传的文件、限制文件大小、设置文件类型限制等。只能用于处理 multipart/form-data 类型的表单数据,它主要用于上传文件。 下面是使用Multer中间件的基本…...

性能监控软件是什么?有哪些优势?
在现代科技驱动的世界中,计算机系统的性能对于企业和个人用户都至关重要。性能监控软件是一种不可或缺的工具,可以帮助我们实时跟踪、分析和优化系统的性能。本文将介绍性能监控软件的概念、其重要性以及如何选择和使用这些工具来提高系统效率。 一、性能…...
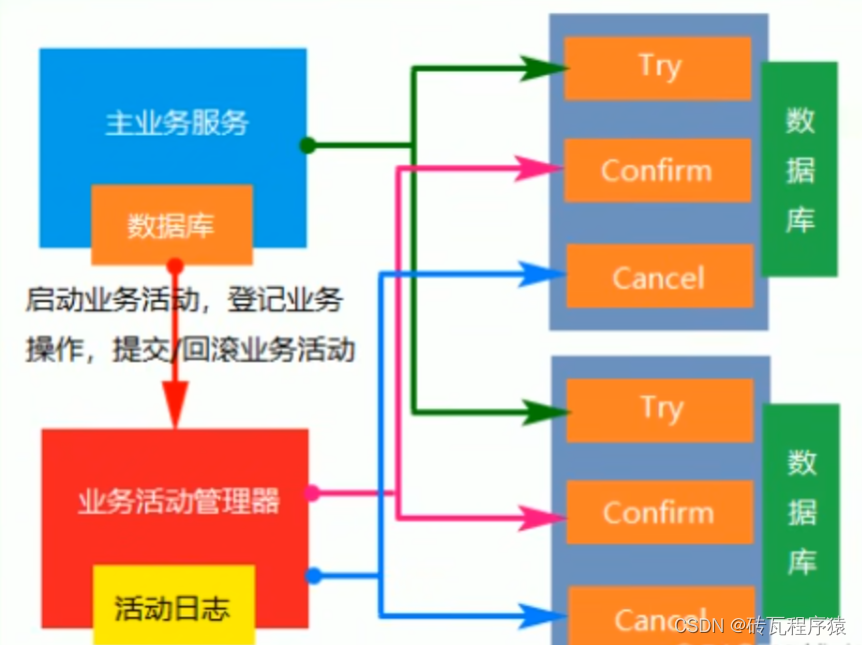
分布式事务及CAP和BASE顶底
一、分布式事务 单体应用肯定就不存在分布式事务了,只有在分布式微服务系统中,各个服务之间通过RPC调用后,每个微服务有自己和数据库的连接,各个微服务的回滚不影响其他的微服务事务,这几必须使用分布式事务来解决分布…...

Django REST Framework完整教程-认证与权限-JWT的使用
文章目录 1.认证(Authentication)与权限(Permission)1.1.视图添加权限1.2.登录验证1.3.常用DRF自带权限类1.4.自定义权限类1.5.全局权限1.6.函数视图权限 2.认证详解2.1.认证方案2.2.如何使用TokenAuthentication? 3.JSON Web Token(JWT)认证3.1.工作原理3.2.安装3.…...
领域内容第18名
恭喜入榜...

[1024]程序员节 一晃6年过去了
加入开发者大军,一晃已是6年有余,从最初的Andoird开发如火如荼,到现在的秋风萧瑟,宛如被秋风吹得只剩躯干的树木,等待来年的焕发新芽。 我本不是一个科班出身的开发者,但是为了生活,说白了为了钱…...

数据结构 | 构造哈夫曼树
template<class T> void Heap<T>::PercolateUp() //为了向上调整为堆,我们需要比较当前节点和其父节点的值,如果父节点的值比当前节点大,则交换它们的值。 { int p size - 1, c (p - 1) / 2;//c表示当前节点的父节点࿰…...

实验室烧杯可以用超声波清洗机吗
实验室烧杯可以用超声波清洗机吗?答案是可以的!超声波清洗机不仅可以清洗实验烧杯,还可以用于清洗实验室中的试管、培养皿、移液管、载玻片、容量瓶、锥形瓶等各类实验器皿。在实验中,如果烧杯清洁不到位,会使得实验数…...
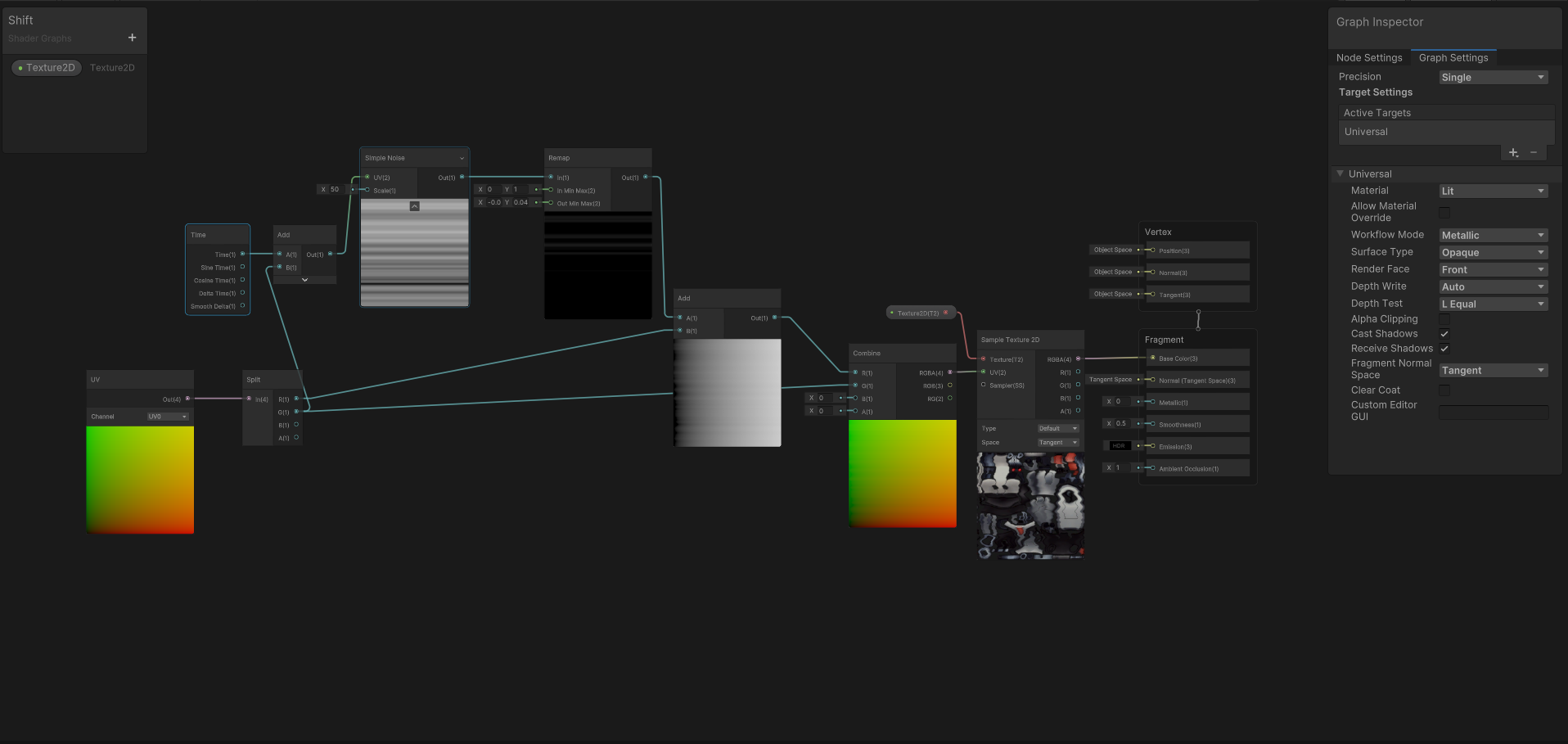
Unity之ShaderGraph如何实现UV抖动
前言 今天我们通过噪波图来实现一个UV抖动的效果。 如下图所示: 关键节点 Time:提供对着色器中各种时间参数的访问 UV:提供对网格顶点或片段的UV坐标的访问。可以使用通道下拉参数选择输出值的坐标通道。 SimpleNoise:根据…...

#力扣:771. 宝石与石头@FDDLC
771. 宝石与石头 - 力扣(LeetCode) 一、Java class Solution {public int numJewelsInStones(String jewels, String stones) {int[] isJewel new int[z 1];for (int i jewels.length() - 1; i > 0; i--) isJewel[jewels.charAt(i)] 1;int cnt …...
【网络协议】聊聊拓扑网络结构与原理
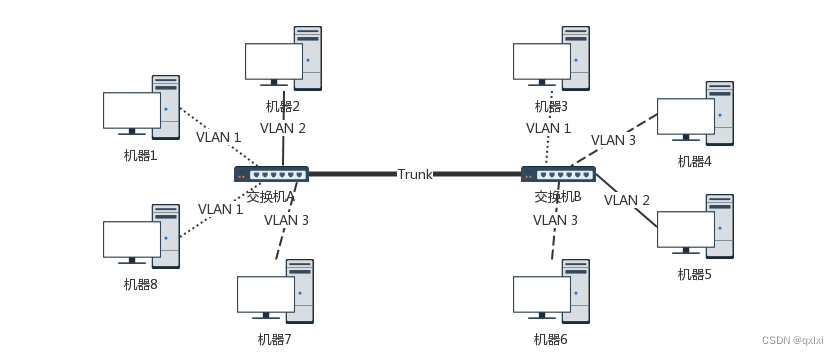
拓扑结构 上一篇我们简单讲述了一种交换机的情况,但是实际的场景是比较复杂的,在一个楼层可能有几十或者上百个接口,那么当知道对方的IP地址,求对方的MAC地址,其实是通过ARP协议进行处理的。 上图是一个两个交换机的…...

uview表单 hooks
在UViewUI库中,使用hooks封装表单二次可以让我们以更灵活的方式使用表单组件。下面是一个示例,展示如何将表单封装成hooks,并以JSON形式传递参数: 首先,我们可以创建一个自定义的Hook来处理表单逻辑。在这个例子中&…...
车载视频如何转换视频格式
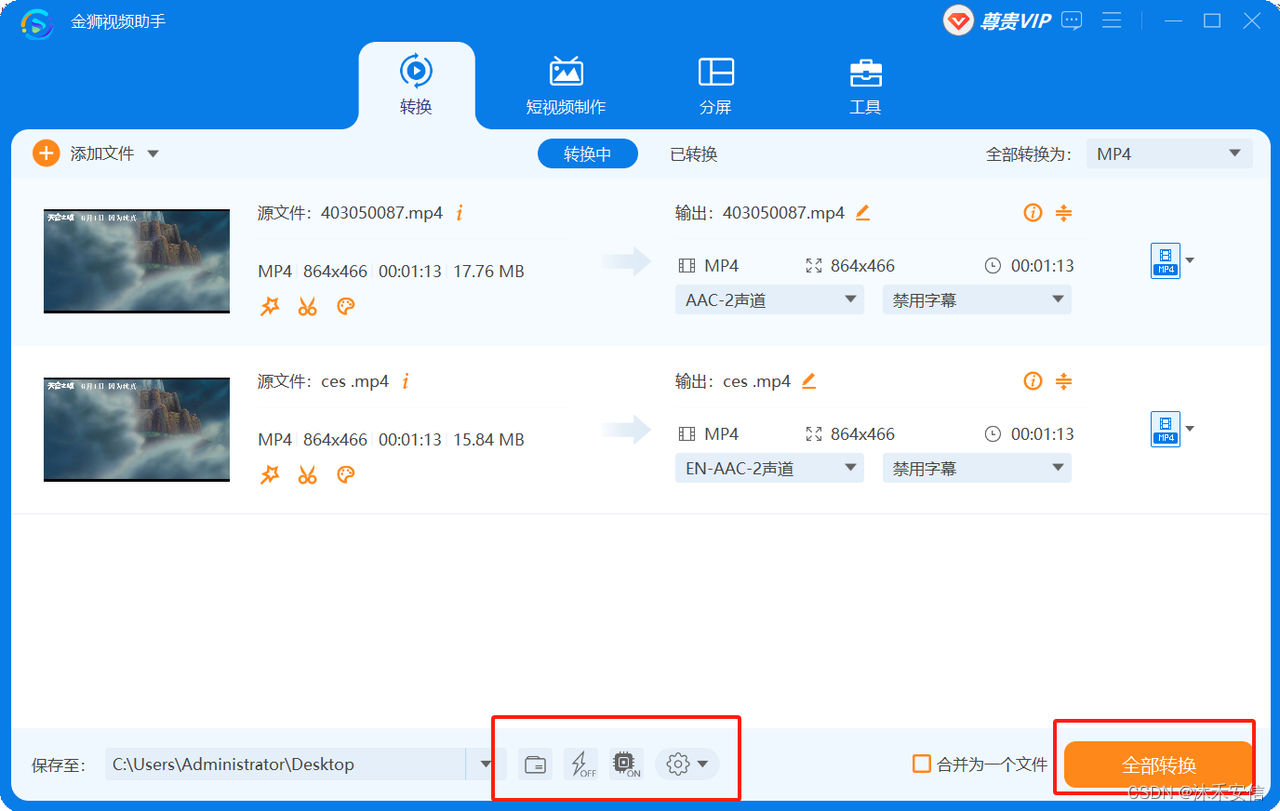
当你收集了多种视频想在车内进行播放,它们可能不会自动播放。你有可能会在屏幕上看到一条消息,显示“文件格式不受支持”,这是因为这些视频可能采用了你的汽车无法识别的格式。 那我们如何才可以转换为车载播放器上运行的最重要且最广泛使用…...
虚拟音频设备软件 Loopback mac中文版软件介绍
创建虚拟音频设备以从应用程序和音频输入设备获取声音,然后将其发送到音频处理应用程序,它就是—Loopback for Mac,Loopback mac为您提供高端工作室混音板的强大功能,有了它在Mac上传递音频会变得很容易。 Loopback for mac中文版…...
Android SurfaceControlViewHost介绍及使用
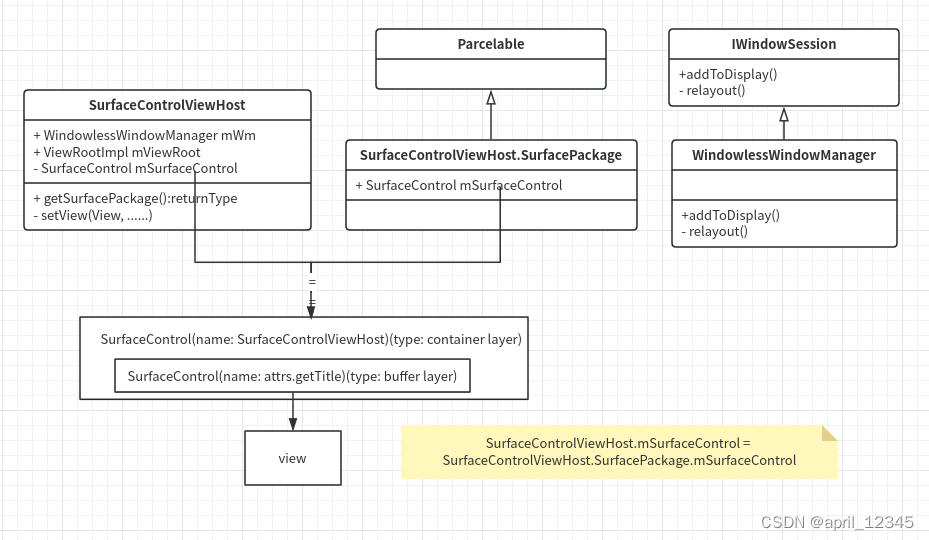
概要介绍 SurfaceControlViewHost是一个工具类, 用于帮助在其他进程中显示本进程的view。 SurfaceControlViewHost 为绘制进程持有,其中的SurfacePackage 交给另外的显示进程,在显示进程中的SurfaceView中通过SurfaceView.setChildSurface…...
微信小程序开发(一)
目录 开发者界面 app.json配置(举例) 组件 样式 像素 flex布局 微信小程序是一种基于微信平台的应用程序开发模式,它可以让开发者使用前端开发技术(如HTML、CSS和JavaScript)开发应用程序,并在微信客户端中运行。以下是微信…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
