Unity Mono和.Net平台浮点算法的区别
static void TestFloat(){{//float speed=2.0f/20;float speed = 0.1f;float distance = 2.0f;long needTime = (long)(distance / speed);Log.Debug($"needTime={needTime}");
#if UNITY_EDITORif (needTime != 19)
#elseif (needTime != 20)//.Net服务器和安卓手机
#endifLog.Warning("平台浮点算法变了");}}static void TestFixInt(){{FixInt fi2 = 20000;FixInt fi1 = 10000;if (fi1 / fi2 != 0.5f){Log.Warning($"TestFixInt,{fi2}/{fi1} != 0.5");}}{FixInt fi2 = 20000;FixInt fi1 = 10000;if (fi2 / fi1 != 2){Log.Warning($"TestFixInt,{fi2}/{fi1} != 2");}}{const long l = 20000;FixInt fi = new(6000);if (l < fi){Log.Warning($"TestFixInt,{l} < {fi}");}}{FixInt fi3 = new(3);FixInt fi5 = new(5);if (fi3 + 1000 < fi5){Log.Warning($"TestFixInt,{fi3} , {fi5}");}}{const long l = 3000;FixInt fi = l;if (fi.RawLong != l){Log.Warning($"TestFixInt,{fi.RawLong} != {l}");}}}static void TestGetPolygonFormation(){var points = TeamFormationComponentSystem.GetPolygonFormation(new(),new() { x = 230.33540344238281f, y = -0.0000019073486328125f, z = 62.280677795410156f },new() { x = -6.1755828857421875f, y = -0.045724689960479736f, z = 9.5355415344238281f },4,2);List<float3> list = new(){new(){x = 230.429f, y = 0.0f, z = 62.135f },new(){ x = 233.077f, y = 0.0f, z = 60.689f },new(){ x = 233.317f, y = 0.0f, z = 57.679f },new(){ x = 230.669f, y = 0.0f, z = 59.125f },};if (points.Count != list.Count){Log.Warning($"TestGetPolygonFormation,{points} != {list}");}for (int i = 0; i <points.Count; ++i){var cal = points[i];var want = list[i];if (!cal.Equals(want)){Log.Warning($"TestGetPolygonFormation,{cal} != {want}");}}}static void TestGetPointOnEllipse(){var radius = 2.82842707633972f;var intervalAngle = 90;var radian = -32.9286422729492f + (intervalAngle * 3);var dChangZhouAngle = -45f;var xShaft = 0.5f * radius;var yShaft = 1f * radius;var ptCenter = new float2(231.872909545898f, 59.9066619873047f);var cal = VectorHelper.GetPointOnEllipse(ptCenter,xShaft,yShaft,radian,dChangZhouAngle); //算出旋转后的向量float3 want = new() { x = 230.669f, y = 0.0f, z = 59.125f };if (!cal.Equals(want)){Log.Warning($"TestGetPointOnEllipse,{cal} != {want}");}}static void TestMath(){var radius = 2.82842707633972f;var intervalAngle = 90;var radian = -32.9286422729492f + (intervalAngle * 3);var dChangZhouAngle = -45f;var xShaft = 0.5f * radius;var yShaft = 1f * radius;var ptCenter = new float2(231.872909545898f, 59.9066619873047f);radian -= dChangZhouAngle;dChangZhouAngle *= VectorHelper.Mathf.Deg2Rad;radian *= VectorHelper.Mathf.Deg2Rad;float dLiXin = math.atan2(yShaft * math.sin(radian), xShaft * math.cos(radian)); //离心角if (dLiXin != -1.46427190303802f){Log.Warning($"TestMath,{dLiXin} ");}if (yShaft != 2.8284270763397221f){Log.Warning($"TestMath,{yShaft} ");}if (dLiXin != -1.4642719030380249f){Log.Warning($"TestMath,{dLiXin} ");}if (dChangZhouAngle != -0.78539818525314298f){Log.Warning($"TestMath,{dChangZhouAngle} ");}if (xShaft != 1.4142135381698611f){Log.Warning($"TestMath,{xShaft} ");}var cosLiXin = math.cos(dLiXin);var sinChangZhouAngle = math.sin(dChangZhouAngle);var sinLiXin = math.sin(dLiXin);var cosChangZhouAngle = math.cos(dChangZhouAngle);if (cosLiXin != 0.10632307827472701f){Log.Warning($"TestMath,{xShaft} ");}if (sinChangZhouAngle != -0.70710676908492998f){Log.Warning($"TestMath,{xShaft} ");}if (sinLiXin != -0.99433165788650502f){Log.Warning($"TestMath,{xShaft} ");}if (cosChangZhouAngle != 0.70710676908492998f){Log.Warning($"TestMath,{xShaft} ");}var x = yShaft * cosLiXin * sinChangZhouAngle + xShaft * sinLiXin * cosChangZhouAngle + ptCenter.x;
#if UNITY_EDITORif (x != 230.665939331055f)
#elseif (x != 230.66592407226563f)
#endif{Log.Warning($"平台浮点加法或乘法算法变了,{x} ");}float y = yShaft * math.cos(dLiXin) * math.cos(dChangZhouAngle) - xShaft * math.sin(dLiXin) * math.sin(dChangZhouAngle) + ptCenter.y;}结论
.Net和安卓手机IL2CPP算法相同
Windows下Unity的Mono算法不同,就它不同
相关文章:

Unity Mono和.Net平台浮点算法的区别
static void TestFloat(){{//float speed2.0f/20;float speed 0.1f;float distance 2.0f;long needTime (long)(distance / speed);Log.Debug($"needTime{needTime}"); #if UNITY_EDITORif (needTime ! 19) #elseif (needTime ! 20)//.Net服务器和安卓手机 #endif…...
】64 - QNX 与 Android GVM 显示 Dump 图片方法汇总)
【SA8295P 源码分析 (二)】64 - QNX 与 Android GVM 显示 Dump 图片方法汇总
【SA8295P 源码分析】64 - QNX 与 Android GVM 显示 Dump 图片方法汇总 一、QNX侧1.1 surfacedump 功能1.2 screenshot 功能二、Android GVM 侧2.1 screencap -p 导出 PNG 图片2.2 screencap 不加 -p 参数,导出 RGB32 图片2.3 dumpsys SurfaceFlinger --display-id 方法系列文…...
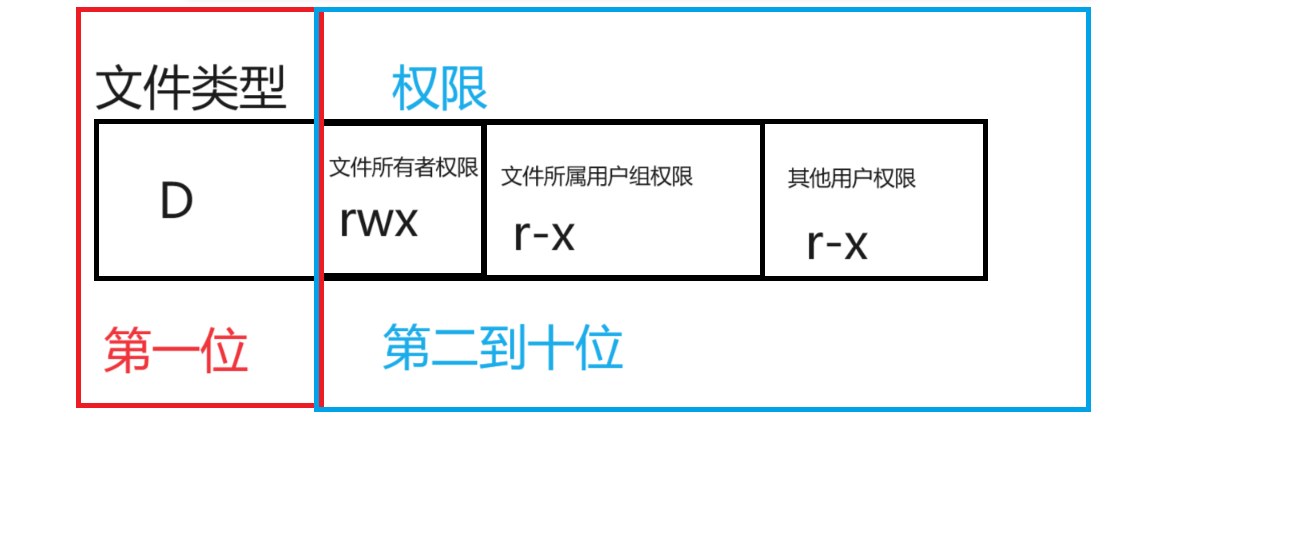
shell命令以及运行原理和lLinux权限
shell命令以及运行原理 什么是shell shell是操作系统的外壳程序统称,我们是通过shell去和操作系统沟通的。 从技术角度,shell最简单的定义就是命令行解释器,主要包含两个功能: 将使用者的命令翻译给核心处理 将核心的处理结果…...
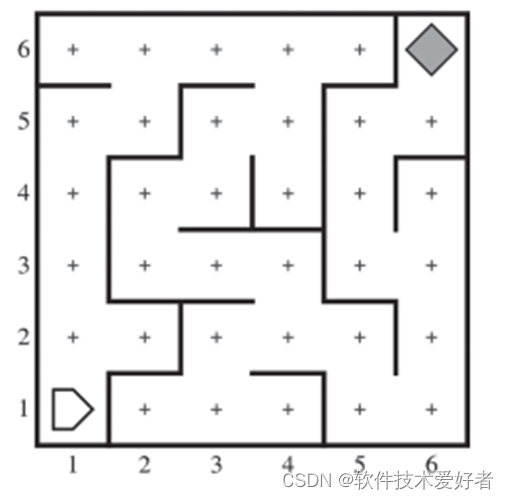
斯坦福JSKarel编程机器人使用介绍
斯坦福JSKarel编程机器人使用介绍 为了避免被编程语言固有的复杂性所困扰,有一个被称为卡雷尔(Karel)机器人的微型世界(microworld)的简化环境,可以让编程初学者从中学习理解编程的基本概念,而…...

SpringBoot中pom.xml不引入依赖, 怎么使用parent父项目的依赖
在Spring Boot项目中,如果你想使用父项目的依赖,而不想在pom.xml中显式引入依赖,你可以使用Maven的继承机制。 首先,确保你的Spring Boot项目是一个子项目,即它继承自一个父项目。要实现这一点,在pom.xml文…...

基于vue3+ts5+vue-router4+pinia2的PC端项目搭建教程
导语:在日常开发中,有时候会在项目中引入 ts 来解决一些 js 的问题,下面就简单介绍一下如何使用 vue3tsrouterpinia 来搭建一个项目。 目录 简介创建安装配置实战 简介 vue3 目前是常用的 vue 版本,提供了组合式 API 以及一些新…...
6个无版权、免费、高清图片素材库
找免费无版权图片素材,就上这6个网站,超高质量,可商用,赶紧收藏! 1、菜鸟图库 https://www.sucai999.com/pic.html?vNTYwNDUx 网站主要为新手设计师提供免费素材,这些素材的质量都很高,类别也…...

什么是响应式设计?响应式设计的基本原理是什么?如何兼容低版本的 IE?
什么是响应式设计: 响应式设计(Responsive Design)是一种Web设计和开发方法,旨在使网站在不同设备和屏幕尺寸上都能提供一致的用户体验。响应式设计的目标是适应多种终端,包括桌面计算机、笔记本电脑、平板电脑和移动设备&#x…...

LeetCode 2906. 构造乘积矩阵【前后缀分解,数组】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

vue3+koa+axios实现前后端通信
vue3koaaxios实现前后端通信 写了一个小demo来实现前后端通信,涉及跨域问题,非常简单可以给大家平时开发的时候参考 服务端: 目录结构如下: router index.js // router的入口文件 // 引入路由 const Router require("koa-router&quo…...
Required MultipartFile parameter ‘file‘ is not present
出现这个原因我们首先想到的是加一个RequestParam("file"),但是还有可能的原因是因为我们的名字有错误 <span class"input-group-addon must">模板上传 </span> <input id"uploadFileUpdate" name"importFileU…...

vue3后台管理系统之layout组件的搭建
1.1静态布局 <template><div class"layout_container"><!-- 左侧导航 --><div class"layout_slider"></div><!-- 顶部导航 --><div class"layout_tabbar"></div><!-- 内容展示区 --><…...

Minio 文件上传(后端处理同文件判断,同一文件秒传)
记录minio 文件上传 MinIO提供多个语言版本SDK的支持,下边找到java版本的文档: 地址:https://docs.min.io/docs/java-client-quickstart-guide.html maven依赖如下: XML <dependency><groupId>io.minio</groupId…...
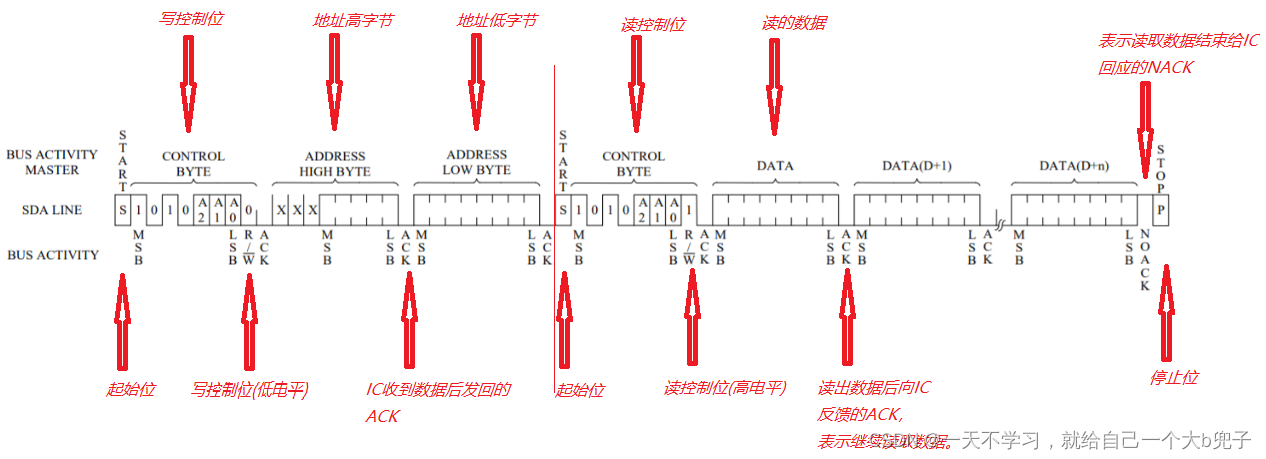
模拟IIC通讯协议(stm32)(硬件iic后面在补)
一、IIC基础知识总结。 1、IIC通讯需要两条线就可以,SCL、SDA。 2、IIC的数据传输的速率,不同的ic是不同的,根据电平维持的延时函数的时间来确定IIC数据传输的速率. 3、IIC的延时函数可以使用延时函数,延时函数一般使用系统滴答时…...

使用注解读取properties配置文件
文章目录 1、背景2、注解方式2.1 PropertySource 、 ConfigurationProperties2.2 读取properties中全部字段值ConfigurationProperties2.3 读取properties中部分字段值:value("${自定义key}") 1、背景 服务中使用到了redis,需要配置redis连接…...

Python---练习:求世界杯小组赛的总成绩(涉及:布尔类型转换为整型)
案例 世界杯案例 需求: 世界杯案例,世界杯小组赛的比赛规则是我们的球队与其他三支球队进行比赛,然后根据总成绩(积分)确定出线资格。小组赛球队实力已知(提示用户输入各球队实力),我们通过一个数字表示。如果我们赢…...

vue3学习源码笔记(小白入门系列)------KeepAlive 原理
目录 说明组件是如何被缓存的,什么时候被激活对于KeepAlive 中组件 如何完成激活的对于KeepAlive 中组件 如何完成休眠的 总结 说明 Vue 内置了 KeepAlive 组件,实现缓存多个组件实例切换时,完成对卸载组件实例的缓存,从而使得组…...
边写代码边学习之mlflow
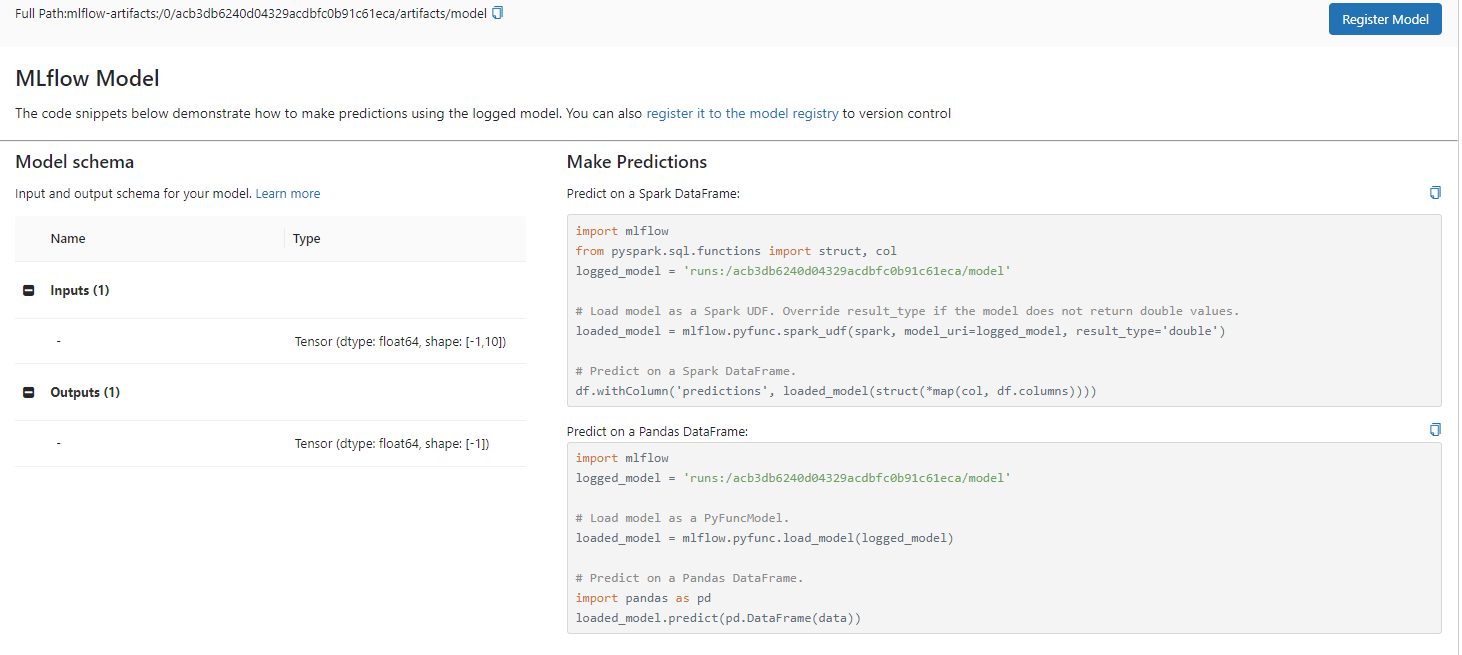
1. 简介 MLflow 是一个多功能、可扩展的开源平台,用于管理整个机器学习生命周期的工作流程和工件。 它与许多流行的 ML 库内置集成,但可以与任何库、算法或部署工具一起使用。 它被设计为可扩展的,因此您可以编写插件来支持新的工作流程、库和…...

基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码
基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码 文章目录 基于吉萨金字塔建造优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.吉萨金字塔建造优化BP神经网络3.1 BP神经网络参数设置3.2 吉萨金字…...

axios的post请求所有传参方式
Axios支持多种方式来传递参数给POST请求。以下是一些常见的方式: 作为请求体: 你可以将参数作为请求体的一部分,通常用于发送表单数据或JSON数据。例如: const data { key1: value1, key2: value2 }; axios.post(/api/endpoint, …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
