统计学习方法 感知机
文章目录
- 统计学习方法 感知机
- 模型定义
- 学习策略
- 学习算法
- 原始算法
- 对偶算法
- 学习算法的收敛性
统计学习方法 感知机
读李航的《统计机器学习》时,关于感知机的笔记。
感知机(perceptron)是一种二元分类的线性分类模型,属于判别模型,是 NN 和 SVM 的基础。
模型定义
感知机:输入空间 X ⊆ R n \mathcal{X}\subseteq \R^n X⊆Rn ,输出空间是 Y = { 1 , − 1 } \mathcal{Y}=\set{1,\,-1} Y={1,−1} ;输入 x ∈ X x\in \mathcal{X} x∈X 表示实例的特征向量,输出 y ∈ Y y\in\mathcal{Y} y∈Y 表示实例的类别。由输入空间到输出空间的如下函数:
f ( x ) = sign ( w ⋅ x + b ) f(x)=\text{sign}(w \cdot x+b) f(x)=sign(w⋅x+b)
称为感知机。其中 w ∈ R n w \in \R^n w∈Rn 称为权重, b ∈ R b\in\R b∈R 称为偏置。
线性方程 w ⋅ x + b w \cdot x+b w⋅x+b 对应特征空间 R n \R^n Rn 中的一个超平面 S S S ,位于两边的点(特征向量)则被分为正、负两类:
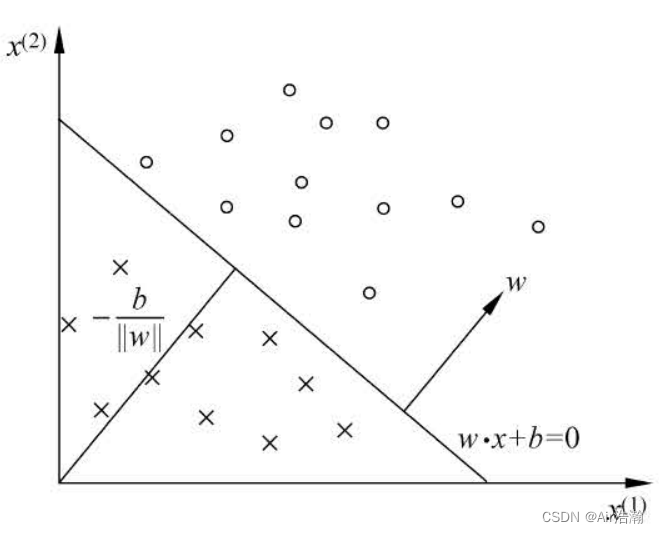
学习策略
当训练数据是完全线性可分的,我们则可以找到一个超平面将正负类的数据完全分开。但数据不完全线性可分时,我们则要定义损失函数,找到一个感知机使得损失函数极小化。(但其实即使完全线性可分,也要定义损失函数,不然怎么学习 [乐.jpg])
很容易想到用分类错误的点的总数作为损失函数,但是这样对 w w w 和 b b b 就不是连续可导的了,不好优化。所以我们选择所有误分类点到超平面 S S S 的总距离作为损失函数。
空间中任意一点 x 0 ∈ R n x_0\in \R^n x0∈Rn 到超平面 S S S 的距离为:
dis ( x 0 , S ) = 1 ∣ ∣ w ∣ ∣ ∣ w ⋅ x 0 + b ∣ \text{dis}(x_0,S)=\frac{1}{||w||}|w\cdot x_0+b| dis(x0,S)=∣∣w∣∣1∣w⋅x0+b∣
- ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 是 w w w 的 L 2 L_2 L2 范数;
其次,对于误分类的数据 ( x i , y i ) (x_i,y_i) (xi,yi) 来说, y i y_i yi 与 f ( x ) f(x) f(x) 符号相反,因此:
− y i ( w ⋅ x i + b ) > 0 -y_i(w\cdot x_i+b)\gt 0 −yi(w⋅xi+b)>0
我们利用这个大于零的性质,可以将误分类点到超平面的距离表示为(因为 y i y_i yi 只有可能是正负 1,所以乘上去也不会改变距离的大小):
dis ( x 0 , S ) = − 1 ∣ ∣ w ∣ ∣ y i ( w ⋅ x i + b ) \text{dis}(x_0,S)=-\frac{1}{||w||}y_i(w\cdot x_i+b) dis(x0,S)=−∣∣w∣∣1yi(w⋅xi+b)
因此,所有误分类点到超平面 S S S 的距离之和:
− 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w ⋅ x i + b ) -\frac{1}{||w||}\sum_{x_i\in M} y_i(w\cdot x_i+b) −∣∣w∣∣1xi∈M∑yi(w⋅xi+b)
- M M M 为被误分类点的集合;
这里不考虑 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 ,即得到感知机的损失函数:
L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) L(w,\,b)=-\sum_{x_i\in M} y_i(w\cdot x_i+b) L(w,b)=−xi∈M∑yi(w⋅xi+b)
去掉 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 对损失函数的优化至关重要, y i ( w ⋅ x i + b ) y_i(w\cdot x_i+b) yi(w⋅xi+b) 被称为样本点的函数间隔,在 SVM 中会涉及到。
学习算法
感知机学习算法的原始形式和对偶形式与第7支待向量机学习法的原始形式和偶形式相对应。
原始算法
给定一个训练数据集:
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1,\,y_1),\,(x_2,\,y_2),\,\cdots,\,(x_N,\,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中 x i ∈ X = R n x_i\in\mathcal{X}=\bold{R}^n xi∈X=Rn , y i ∈ Y = { − 1 , 1 } y_i\in\mathcal{Y}=\{-1,\,1\} yi∈Y={−1,1} , i = 1 , 2 , ⋯ , N i=1,\,2,\,\cdots,\,N i=1,2,⋯,N ,求参数 w w w 和 b b b ,使得以下损失函数极小化:
min w , b L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) \min_{w,\,b}L(w,\,b)=-\sum_{x_i\in M}y_i(w\cdot x_i +b) w,bminL(w,b)=−xi∈M∑yi(w⋅xi+b)
我们采用随机梯度下降法来学习参数 w w w 和 b b b ,梯度为:
∇ w L ( w , b ) = − ∑ x i ∈ M y i x i ∇ b L ( w , b ) = − ∑ x i ∈ M y i \begin{align} \nabla_wL(w,\,b)=&\,-\sum\limits_{x_i\in M}y_ix_i \\ \nabla_bL(w,\,b)=&\,-\sum\limits_{x_i\in M}y_i \\ \end{align} ∇wL(w,b)=∇bL(w,b)=−xi∈M∑yixi−xi∈M∑yi
但学习的时候并不是一次使 M M M 中所有的误分类点都梯度下降,而是一次随机选取一个误分类点使其梯度下降。
算法:感知机学习算法的原始形式
输入:训练数据集 T T T ,学习率 η \eta η ( 0 < η ≤ 1 0 \lt\eta\leq 1 0<η≤1);
输出: w w w , b b b ,感知机模型 f ( x ) = sign ( w ⋅ x + b ) f(x)=\text{sign}(w\cdot x+b) f(x)=sign(w⋅x+b) ;
- 选取初值 w 0 w_0 w0 和 b 0 b_0 b0 ;
- 在训练集中选取数据 ( x i , y i ) (x_i,\,y_i) (xi,yi) ;
- 若 y i ( w ⋅ x i + b ) ≤ 0 y_i(w\cdot x_i+b) \leq 0 yi(w⋅xi+b)≤0 :
w ← w + η y i x i b ← b + η y i \begin{align} w \leftarrow&\, w+\eta y_ix_i \\ b \leftarrow&\, b+\eta y_i \end{align} w←b←w+ηyixib+ηyi
- 若当前训练集中仍有误分类点,则跳转至 2. ,否则结束;
对偶算法
我们前面对误分类点修改参数时的形式为:
w ← w + η y i x i b ← b + η y i \begin{align} w \leftarrow&\, w+\eta y_ix_i \\ b \leftarrow&\, b+\eta y_i \end{align} w←b←w+ηyixib+ηyi
因此,我们可以认为模型参数是训练样本值的线性组合,即最后学习到的 w w w 和 b b b 可以表示为:
w = ∑ i = 1 N α i y i x i b = ∑ i = 1 N α i y i \begin{array}{c} w=\sum\limits_{i=1}^N \alpha_iy_ix_i \\ b=\sum\limits_{i=1}^{N}\alpha_iy_i \end{array} w=i=1∑Nαiyixib=i=1∑Nαiyi
这里 α i ≥ 0 \alpha_i \geq 0 αi≥0 ( i = 1 , 2 , ⋯ , N i=1,2,\cdots,N i=1,2,⋯,N)。
算法:感知机学习算法的对偶形式
输入:训练数据集 T T T ,学习率 η \eta η ( 0 < η ≤ 1 0 \lt\eta\leq 1 0<η≤1);
输出: α \alpha α , b b b ,感知机模型 f ( x ) = sign ( ∑ j = 1 N α j y j x j ⋅ x + b ) f(x)=\text{sign}(\sum\limits_{j=1}^N \alpha_jy_jx_j\cdot x+b) f(x)=sign(j=1∑Nαjyjxj⋅x+b) ;
- 初始化: α ← 0 \alpha \leftarrow 0 α←0 , b ← 0 b \leftarrow 0 b←0 ;
- 在训练集中选取数据 ( x i , y i ) (x_i,\,y_i) (xi,yi) ;
- 若 y i ( ∑ j = 1 N α j y j x j ⋅ x + b ) ≤ 0 y_i(\sum\limits_{j=1}^N \alpha_jy_jx_j\cdot x+b) \leq 0 yi(j=1∑Nαjyjxj⋅x+b)≤0 ,
α i ← α i + η b ← b + η y i \begin{align} \alpha_i \leftarrow&\, \alpha_i+\eta \\ b \leftarrow&\, b+\eta y_i \end{align} αi←b←αi+ηb+ηyi
- 若当前训练集中仍有误分类点,则跳转至 2. ,否则结束;
为了方便,可以预先将训练集中的实例间的内积计算出来并以矩阵的形式存储,即 Gram 矩阵:
G = [ x i ⋅ x j ] N × N \bold{G}=[x_i \cdot x_j]_{N\times N} G=[xi⋅xj]N×N
学习算法的收敛性
当数据集不可分时,显然上述算法会震荡。现在证明,对于线性可分数据集,感知机学习算法原始形式收敛,即经过有限次迭代就可以得到一个将数据集完全正确划分的分离超平面及感知机模型。
为了数学推导方面,我们将偏置 b b b 放入权重向量 w w w ,记作 w ^ = [ w t , b ] T \hat{w}=[w^t,\,b]^T w^=[wt,b]T 。同样将输入向量进行增广,得到 x ^ = [ x T , 1 ] T \hat{x}=[x^T,\,1]^T x^=[xT,1]T ,显然:
w ^ ⋅ x ^ = w ⋅ x + b \hat{w}\cdot\hat{x}=w\cdot x+b w^⋅x^=w⋅x+b
Th 2.1(Novikoff) 设训练数据集 T T T 是线性可分的,则:
- 存在满足条件 ∣ ∣ w ^ o p t ∣ ∣ = 1 ||\hat{w}_{opt}||=1 ∣∣w^opt∣∣=1 的超平面 w ^ o p t ⋅ x ^ = 0 \hat{w}_{opt}\cdot \hat{x}=0 w^opt⋅x^=0 将训练数据集完全正确分开,且存在 γ > 0 \gamma >0 γ>0 ,对所有 i = 1 , 2 , ⋯ , N i=1,\,2,\,\cdots,\,N i=1,2,⋯,N ,都有:
y i ( w ^ o p t ⋅ x ^ i ) = y i ( w o p t ⋅ x i + b o p t ) ≥ γ y_i(\hat{w}_{opt}\cdot \hat{x}_{i})=y_i(w_{opt}\cdot x_{i}+b_{opt})\geq \gamma yi(w^opt⋅x^i)=yi(wopt⋅xi+bopt)≥γ
- 令 R = max 1 ≤ i ≤ N ∣ ∣ x ^ i ∣ ∣ R=\max\limits_{1\leq i\leq N}||\hat{x}_{i}|| R=1≤i≤Nmax∣∣x^i∣∣ ,则感知机算法在训练数据集上的误分类次数 k k k 满足:
k ≤ ( R γ ) 2 k\leq \left(\frac{R}{\gamma}\right)^2 k≤(γR)2
证明:第一点较为简单。因为训练数据集线性可分,因此存在超平面 ( w o p t , b o p t ) (w_{opt},\,b_{opt}) (wopt,bopt) 可将数据集完全正确分开。只要令:
γ = min i { y i ( w o p t ⋅ x i + b o p t ) } \gamma=\min_{i}\{ y_i(w_{opt}\cdot x_i+b_{opt}) \} γ=imin{yi(wopt⋅xi+bopt)}
就有:
y i ( w ^ o p t ⋅ x ^ i ) = y i ( w o p t ⋅ x i + b o p t ) ≥ γ y_i(\hat{w}_{opt}\cdot \hat{x}_{i})=y_i(w_{opt}\cdot x_{i}+b_{opt})\geq \gamma yi(w^opt⋅x^i)=yi(wopt⋅xi+bopt)≥γ
现在来看第二点,看起来还蛮神奇的。感知机算法从 w ^ 0 = 0 \hat{w}_0=0 w^0=0 开始,记每一次迭代得到的参数为 w ^ k \hat{w}_k w^k 。第 k k k 个参数下,记 ( x i , y i ) (x_i,\,y_i) (xi,yi) 是被误分类的实例,则条件是:
y i ( w ^ k − 1 ⋅ x ^ i ) = y i ( w k − 1 ⋅ x i + b k − 1 ) ≤ 0 y_i(\hat{w}_{k-1}\cdot \hat{x}_i)=y_i(w_{k-1}\cdot x_i + b_{k-1})\leq 0 yi(w^k−1⋅x^i)=yi(wk−1⋅xi+bk−1)≤0
w w w 和 b b b 的更新是:
w k ← w k − 1 + η y i x i b k ← b k − 1 + η y i \begin{align} w_k \leftarrow&\, w_{k-1}+\eta y_ix_i \\ b_k \leftarrow&\, b_{k-1}+\eta y_i \end{align} wk←bk←wk−1+ηyixibk−1+ηyi
即:
w ^ k = w ^ k − 1 + η y i x ^ i \hat{w}_k=\hat{w}_{k-1}+\eta y_i\hat{x}_i w^k=w^k−1+ηyix^i
下面证明两个不等式:
① 由于我们是从 w ^ 0 = 0 \hat{w}_0=0 w^0=0 开始的,因此迭代过程中的参数应当从小到大越来越接近 w ^ o p t \hat{w}_{opt} w^opt ,即 w k w_{k} wk 与 w o p t w_{opt} wopt 的内积越来越大:
$$
\begin{align}
\hat{w}k\cdot \hat{w}{opt} =&, \hat{w}{k-1}\cdot \hat{w}{opt}+\eta y_i\hat{w}{opt}\cdot\hat{x}i \
\geq &, \hat{w}{k-1}\cdot \hat{w}{opt}+\eta \gamma \
\geq &, \hat{w}{k-2}\cdot \hat{w}{opt}+2\eta \gamma \
\geq &, \cdots \
\geq &, k\eta \gamma
\end{align}
$$
- 第二个大于等于是因为,我们已经假设了 γ \gamma γ 是最小的 y i w ^ o p t x ^ i y_i\hat{w}_{opt}\hat{x}_i yiw^optx^i ,因此任意 i i i 都有 y i w ^ o p t x ^ i ≥ γ y_i\hat{w}_{opt}\hat{x}_i\geq \gamma yiw^optx^i≥γ ;
即:
w ^ k ⋅ w ^ o p t ≥ k η γ \hat{w}_k\cdot \hat{w}_{opt}\geq k\eta \gamma w^k⋅w^opt≥kηγ
② 由于我们是从 w ^ 0 = 0 \hat{w}_0=0 w^0=0 开始的,因此迭代过程中的参数更新过大时,就会被后续的迭代给“拉”回来:
$$
\begin{align}
||\hat{w}k||2=&,||\hat{w}_{k-1}||2+2\eta y_i\hat{w}{k-1}\cdot \hat{x}i+\eta2||\hat{x}_i||2 \
\leq &, ||\hat{w}{k-1}||2+\eta||\hat{x}_i||2 \
\leq &, ||\hat{w}{k-1}||^2+\eta R^2 \
\leq &, ||\hat{w}{k-2}||^2+2\eta R^2 \
\leq &, \cdots \
\leq &, k\eta2R2
\end{align}
$$
- 第一个等号是因为:
∣ ∣ w ^ k ∣ ∣ 2 = w ^ k T w ^ k = ( w ^ k − 1 + η y i x ^ i ) T ( w ^ k − 1 + η y i x ^ i ) = ( w ^ k − 1 T + η y i x ^ i T ) ( w ^ k − 1 + η y i x ^ i ) = w ^ k − 1 T w ^ k − 1 + η y i ( w ^ k − 1 T x ^ i + x ^ i T w ^ k − 1 ) + η 2 y i 2 x ^ i T x ^ i = ∣ ∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 ⋅ x ^ i + η 2 ∣ ∣ x ^ i ∣ ∣ 2 (有 y i 2 = 1 ) \begin{align} ||\hat{w}_k||^2=&\,\hat{w}_k^T\hat{w}_k \\ =&\,(\hat{w}_{k-1}+\eta y_i\hat{x}_i)^T(\hat{w}_{k-1}+\eta y_i\hat{x}_i) \\ =&\,(\hat{w}_{k-1}^T+\eta y_i\hat{x}_i^T)(\hat{w}_{k-1}+\eta y_i\hat{x}_i) \\ =&\,\hat{w}_{k-1}^T\hat{w}_{k-1}+\eta y_i(\hat{w}_{k-1}^T\hat{x}_i+\hat{x}_i^T\hat{w}_{k-1})+\eta^2y_i^2\hat{x}_i^T\hat{x}_i \\ =&\,||\hat{w}_{k-1}||^2+2\eta y_i\hat{w}_{k-1}\cdot \hat{x}_i+\eta^2||\hat{x}_i||^2 \quad\text{(有$\,y_i^2=1$)} \end{align} ∣∣w^k∣∣2=====w^kTw^k(w^k−1+ηyix^i)T(w^k−1+ηyix^i)(w^k−1T+ηyix^iT)(w^k−1+ηyix^i)w^k−1Tw^k−1+ηyi(w^k−1Tx^i+x^iTw^k−1)+η2yi2x^iTx^i∣∣w^k−1∣∣2+2ηyiw^k−1⋅x^i+η2∣∣x^i∣∣2(有yi2=1)
- 第二个小于等于是因为我们假设 ( x i , y i ) (x_i,\,y_i) (xi,yi) 是被误分类的实例,因此 y i w ^ k − 1 ⋅ x ^ i < 0 y_i\hat{w}_{k-1}\cdot \hat{x}_i<0 yiw^k−1⋅x^i<0 ;
- 第三个小于等于是因为我们假设 R R R 是最大的特征向量的模,因此对于任意 i i i 都有 R ≥ ∣ ∣ x ^ i ∣ ∣ R \geq ||\hat{x}_i|| R≥∣∣x^i∣∣ ;
即:
∣ ∣ w ^ k ∣ ∣ 2 ≤ k η 2 R 2 ||\hat{w}_k||^2\leq k\eta^2R^2 ∣∣w^k∣∣2≤kη2R2
综合不等式 ① 和 ② 得:
k η γ ≤ w ^ k ⋅ w ^ o p t ≤ ∣ ∣ w ^ k ∣ ∣ ∣ ∣ w ^ o p t ∣ ∣ ≤ k η R ⇒ k 2 γ 2 ≤ k R 2 \begin{array}{c} k\eta \gamma \leq \hat{w}_k\cdot \hat{w}_{opt} \leq ||\hat{w}_{k}||\,||\hat{w}_{opt}|| \leq \sqrt{k}\eta R \\ \Rightarrow k^2\gamma^2 \leq kR^2 \end{array} kηγ≤w^k⋅w^opt≤∣∣w^k∣∣∣∣w^opt∣∣≤kηR⇒k2γ2≤kR2
- 第二个小于等于是柯西不等式, x ⋅ y = ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ cos θ ≤ ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ x\cdot y=||x||\,||y||\,\cos\theta\leq ||x||\,||y|| x⋅y=∣∣x∣∣∣∣y∣∣cosθ≤∣∣x∣∣∣∣y∣∣ ,其中 θ \theta θ 是两个向量的夹角。
于是:
k ≤ ( R γ ) 2 k\leq \left(\frac{R}{\gamma}\right)^2 k≤(γR)2
该定理表明,误分类次数 k k k 是有上界的,即训练集线性可分时,感知机学习算法原始形式迭代是收敛的。
相关文章:

统计学习方法 感知机
文章目录 统计学习方法 感知机模型定义学习策略学习算法原始算法对偶算法 学习算法的收敛性 统计学习方法 感知机 读李航的《统计机器学习》时,关于感知机的笔记。 感知机(perceptron)是一种二元分类的线性分类模型,属于判别模型…...
之wc)
Linux命令(103)之wc
linux命令之wc 1.wc介绍 linux命令wc是用来统计文件的字数、行数和字节数 2.wc用法 wc [参数] [filename] wc参数 参数说明-l统计总行数,备注:常用于查看进程是否启动-L统计最长一行的字符数-c统计字节数-m统计字符数-w统计单词数 3.实例 3.1.统计…...

京东店铺公司名爬虫
内容仅供学习参考,如有侵权联系删除 先通过京东非自营的店铺名拿到的公司名,再通过公司名称去其他平台拿到联系方式(代码省略) from aioscrapy.spiders import Spider from aioscrapy.http import Request, FormRequest import dd…...

如何解决不同浏览器的样式兼容性问题?
目录 1. 理解浏览器差异: 2. 使用标准CSS属性和值: 3. CSS Reset 或 Normalize: 4. 使用浏览器引擎前缀: 5. 使用CSS兼容性工具: 6. 测试和调试: 7. 使用Polyfill: 8. 条件注释…...

C++ 中迭代器的使用
在C中,"iter"通常是一个缩写,代表迭代器(iterator),用于遍历容器类(如数组、列表、向量等)中的元素。迭代器允许你按顺序访问容器中的元素,而无需了解底层容器的实现细节。…...
如何使用BERT生成单词嵌入?
阿比贾特萨拉里 一、说明 BERT,或来自变形金刚(Transformer)的双向编码器表示,是由谷歌开发的强大语言模型。它已广泛用于自然语言处理任务,例如情感分析、文本分类和命名实体识别。BERT的主要特征之一是它能够生成单词…...
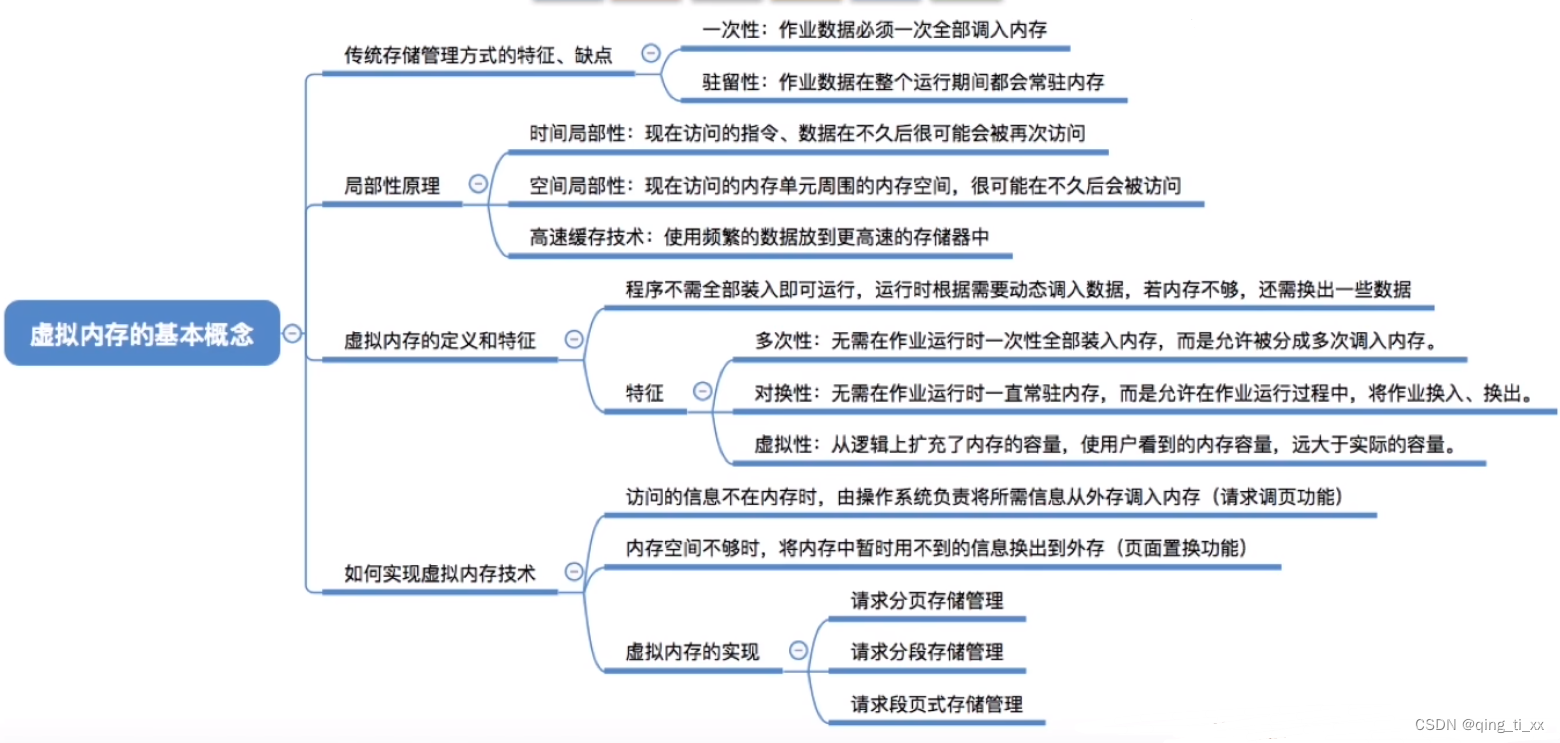
第三章 内存管理 十一、虚拟内存的基本概念
目录 一、传统存储管理 1、缺点 二、局部性原理 1、时间局部性: 2、空间局部性: 三、虚拟内存的定义和特征 1、结构 编辑 2、定义 3、特征 (1)多次性: (2)对换性: (3)…...

web前端面试-- http的各个版本的区别(HTTP/0.9、HTTP/1.0、HTTP/1.1、HTTP/2.0、HTTP/3.0)
本人是一个web前端开发工程师,主要是vue框架,整理了一些面试题,今后也会一直更新,有好题目的同学欢迎评论区分享 ;-) web面试题专栏:点击此处 http的各个版本的区别 HTTP(超文本传输协议&…...
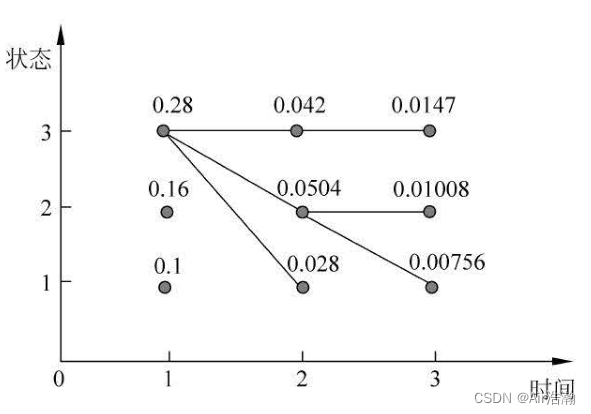
统计学习方法 隐马尔可夫模型
文章目录 统计学习方法 隐马尔可夫模型基本概念概率计算问题直接计算法前向算法后向算法前向概率和后向概率 学习问题监督学习算法Baum-Welch 算法E 步M 步参数估计公式算法描述 解码问题近似算法Viterbi 算法 统计学习方法 隐马尔可夫模型 读李航的《统计学习方法》时&#x…...

Cypress 与 Selenium WebDriver
功能测试自动化工具的王座出现了新的争夺:Cypress.io。赛普拉斯速度快吗?是的。赛普拉斯是交互式的吗?是的。赛普拉斯可靠吗?你打赌。最重要的是……这很酷! 但 Cypress 是Selenium WebDriver的替代品吗?S…...

Leetcode 第 365 场周赛题解
Leetcode 第 365 场周赛题解 Leetcode 第 365 场周赛题解题目1:2873. 有序三元组中的最大值 I思路代码复杂度分析 题目2:2874. 有序三元组中的最大值 II思路代码复杂度分析思路2 题目3:2875. 无限数组的最短子数组思路代码复杂度分析 题目4&a…...

什么是软件测试? 软件测试都有什么岗位 ?软件测试和调试的区别? 软件测试和开发的区别?软件测试等相关概念入门篇
1、什么是软件测试? 常见理解: 软件测试就是找BUG,发现缺陷 真正理解: 软件测试就是验证软件产品特性是否满足用户的需求 测试定义: 测试人员验证软件是否符合需求的这个过程就是测试 2、为什么要有测试 标准情况下&a…...

VI/VIM的使用
1、vi的基本概念 基本上vi可以分为三种状态,分别是命令模式(command mode)、插入模式(Insert mode)和底行模式(last line mode),各模式的功能区分如下: 1) 命令行模…...

【虹科干货】Redis Enterprise vs ElastiCache——如何选择缓存解决方案?
使用Redis 或 Amazon ElastiCache 来作为缓存加速已经是业界主流的解决方案,二者各有什么优势?又有哪些区别呢? 文况速览: - Redis 是什么? - Redis Enterprise 是什么? - Amazon ElastiCache 是什么&…...
2.2.2 交换机间相同vlan的通信
实验2.2.2 交换机间相同vlan的通信 一、任务描述二、任务分析三、实验拓扑四、具体要求五、任务实施1.设置交换机的名称,创建VLAN,配置access并分配接口。对两台交换机进行相同的VLAN划分,下面是SWA配置过程,同理可实现SWB的配置。…...

C的魅力在于指针
原有的adrv9025 代理框架很好用,在其原有的平台上做改进...

【Linux常用命令14】Linux系统监控常用命令
proc文件系统 /proc/cmdline 加载kernel时的相关指令与参数 /proc/cpuinfo CPU相关信息,包含频率、类型与运算功能 /proc/devices 记录了系统各个主要设备的主设备号码 /proc/filesystems 记录系统加载的文件系统 /proc/loadavg 平均负载值 top看到就是这个 /proc/…...

Python Watchdog:高效的文件系统监控
1. 写在前面 在软件开发中,有时候需要通过 Python 去监听指定区域文件或目录的创建、修改,或者删除,从而引发特定的事件处理。本篇博客为你介绍第三方模块 Watchdog 实现对文件事件的监控。 公众号: 滑翔的纸飞机 2. Watchdog 2…...

C++中多态的原理【精华】
虚函数表 通过一道题我们先感受一下编译器针对多态的处理 #include <iostream> using namespace std;class Base { public:virtual void Func1(){cout << "Func1()" << endl;} private:int _b 1;char _c };int main() {cout << sizeof(B…...

亿赛通电子文档安全管理系统 Update.jsp SQL注入
目录 0x01 漏洞介绍 0x02 影响产品 0x03 语法特征 0x04 漏洞复现页面 0x05 漏洞修复建议 0x01 漏洞介绍 亿赛通电子文档安全管理系统是国内最早基于文件过滤驱动技术的文档加解密产品之一,保护范围涵盖终端电脑(Windows、Mac、Linux系统平台&#…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
