线性代数3:矢量方程

一、前言
欢迎回到系列文章的第三篇文章,内容是线性代数的基础知识,线性代数是机器学习背后的基础数学。在我之前的文章中,我介绍了梯队矩阵形式。本文将介绍向量、跨度和线性组合,并将这些新想法与我们已经学到的内容联系起来。本文最好与David C. Lay,Steven R. Lay和Judi J. McDonald的线性代数及其应用一起阅读。将此系列视为配套资源。
二、R²、R³ 和 Rⁿ 中的矢量
到目前为止,我们已经了解了矩阵,它是数字数组,如果我们只有一个数字数组(单数)怎么办?看向量:一种特殊类型的矩阵,大小为 m x 1,其中 m 表示向量中的行数或条目数。回想一下,矩阵大小的表示法是 m x n,其中 m 等于行数,而 n 对应于列数。向量将始终只有一列,但具有任意数量的行。


具有两个条目的所有向量的集合是 R²。R 封装了整个实数集,因此 R² 是实数的所有可能点 (x, y) 的二维空间是有道理的。
向量可以是 R²、R³、R⁴ ...Rⁿ,请注意向量空间的维度对应于向量中的条目数。

您最终可能会遇到奇特的零向量(简单地写为 0),这是一个所有条目均为零的向量。虽然这看起来像是一个小细节,但我们稍后会发现它对线性代数中一些最重要的思想具有重要意义。
三、几何可视化
到目前为止,矩阵和向量已经被描述、解释和注释为数学上的,而物理学中的向量被描述为具有大小和方向的量。两者都同样正确;下面以 R² 为单位的矢量图形可视化将矢量的两个定义统一起来。

重要的是要记住,R² 中的向量是有序对,而高维向量空间中的向量是有序元组(具有定义顺序的数字列表)。两个向量可能与它们的条目具有完全相同的数字,但如果它们的条目顺序不同,则向量也不相同,如上图所示。
R³ 中的向量也可以可视化,我们只需添加一个第三个轴,因为我们有一个额外的条目。除了R³之外,图形向量变得更加复杂,因为很难处理描绘高维空间。

四、向量的代数性质
对于任何给定向量空间中的所有向量 u、v、w 以及标量 c 和 d:以下代数性质¹ 成立:
(i) 交换*:u + v = v + u
(二) 结合*: (u + v) + w = w + (v + w )
(三)加性恒等式:U+0=0+U=U
(iv) 加法逆: u + (-u) = -u + u = 0
(v) 向量分布:c(u + v) = c u + cv
(vi) 使用标量分布:(c + d)u = c u + d u
(vii) 与标量关联:c(d u) = (cd)u
这些属性与向量加法和标量乘法的操作相关联。
要添加两个向量,将相应的条目相加以生成向量和。这意味着两个不同大小的向量的向量加法是未定义的。为了添加两个向量,它们必须具有相同数量的条目!此条件源于向量加法的执行方式。

使用标量乘法,对于给定的标量 c 和向量 u,标量倍数为 c u,其中 u 中的每个条目都已乘以标量 c。

这两个操作可以一起使用;正如您将在下一节中发现的那样,组合形成线性代数的核心概念:线性组合。
五、线性组合
假设我们有向量 v₁、v₂、...Rⁿ 中的 vₐ 我们得到了标量(也称为权重)c₁、c₂、...cₐ,可以是任何实数,包括零。线性组合是由标量倍数之和定义的向量,c₁v₁ + c₂v₂ + ... + cₐvₐ。²

之前,我们已经探讨了线性代数中的存在概念,给定一个矩阵,是否至少存在一个解决方案?换句话说,矩阵的缩减/行梯队形式是否存在不一致?如果是这样,则不存在解决方案。如果没有,那么至少有一个解决方案可以。这个基本存在问题与线性代数中的许多思想有关,线性组合也不例外。
我们说向量 b 是一组向量 v₁、v₂、. 的线性组合。Rⁿ 中的 vₐp,如果存在一组权重 c₁、c₂、...Cₐ(溶液),使得 C₁v₁ + C₂v₂ + ... + CₐVₐ = b。
为了确定 b 是否是线性组合,我们可以使用向量加法和标量乘法的运算将我们的线性组合方程重新排列:c₁v₁ + c₂v₂ + ... + cₐvₐp = b 成我们已经非常熟悉的符号。这种重排过程也揭示了为什么弄清楚向量b是否是一组向量的线性组合是一个存在问题。

上述解释旨在强调为什么存在问题和矩阵行约简与线性组合有关,并在一般意义上演示了这一思想。让我们看一个更具体的例子。
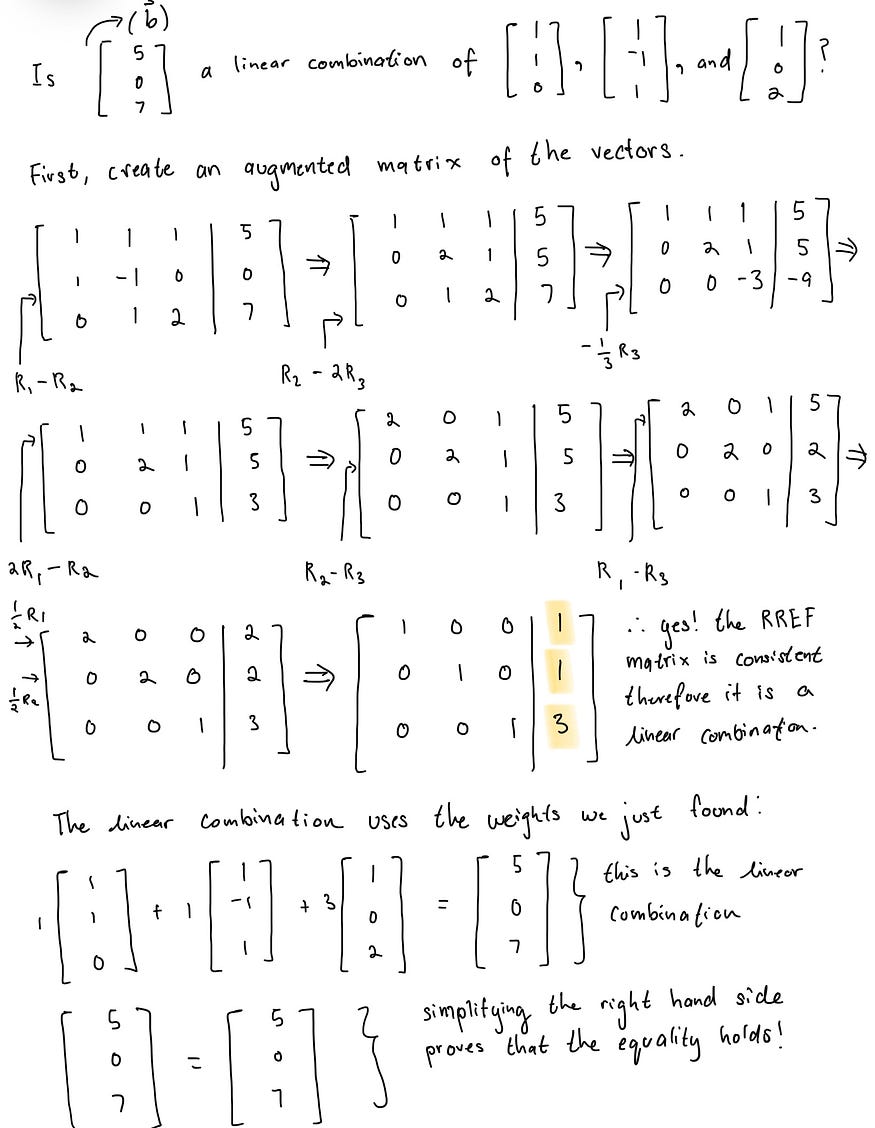
在上面的例子中,将行约简矩阵缩减为缩减行梯队形式后,我们发现解决方案确实存在!
但是,让我们考虑行缩减梯队形式的增强矩阵的情况,行 [0, 0, ... |b],其中 b ≠ 0,这意味着向量 b 不能写成一组向量的线性组合。换句话说,向量 b 对于我们的向量集来说是遥不可及的,或者(这是下一节的一个很好的续集)向量 b 不在向量集的范围内。
六、一组向量的跨度
向量 v₁、v₂、...Rⁿ 中的 vₐ 被称为 Rⁿ 的子集,由 v₁、v₂、...Vₐ。矢量 v₁、v₂、...vₐ 表示为 Span{v₁, v₂, ...vₐ} 并且是可以写为 c₁v₁ + c₂v₂ + ... + cₐvₐ.³ 另一种思考方式是跨度包含所有可以写为向量 v₁、v₂、...Vₐ。
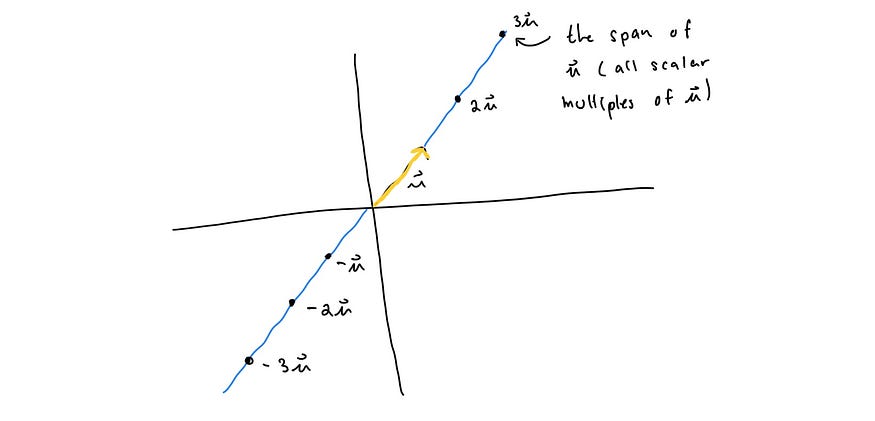
我们可以找到给定任意数量的向量的集合的跨度。假设我们有一组奇异向量 v₁。然后,Span{v₁} 将是 v₁ 的所有标量倍数,因为在这种情况下唯一可以应用的操作是标量乘法(至少需要两个向量来执行向量加法)。Span{v₁} 包含 v₁ 可以到达的所有向量。
如果我们要可视化跨度,它将是一条穿过 v₁ 和原点的直线,因为只有一个向量,线性组合(向量倍数)无法改变方向。下图进一步说明了这一点。
考虑两个向量在不同方向上的跨度(R²),这两个向量可以做出哪些可能的线性组合?换句话说,R² 中的向量可以写成这两个向量的线性组合是什么?

对于上述情况,经过进一步调查,似乎 u 和 v 跨越了整个 R²!这意味着 R² 中的任何向量都可以写为 u 和 v 的线性组合。在以后的文章中,我们将探讨线性独立性的概念,该概念将用于具体证明u和v跨越R²。
七、结论
向量、线性组合和跨度使我们更深入地进入了线性代数的丰富领域。这些基本概念有助于我们理解向量空间的结构以及不同向量集之间的关系。随着我们的进一步发展,您会发现这些想法不断浮出水面,因为它们与其他核心概念相关联。同样,我希望你能花一些时间思考一下我们迄今为止学到的一切(解决方案的存在、行梯队形式)是如何与这些新概念紧密相连的。
八、总结
在本章中,我们了解了:
- R²、R³ 和 Rⁿ 中的向量:向量是一种特殊类型的矩阵,大小为 m x 1。 一个向量可以有任意数量的条目,但只有一列。我们发现也可以有一个零向量,一个所有条目均为零的向量。
- 矢量的几何可视化:矢量可以用图形表示,这有助于理解大小和方向的想法来自哪里。
- 向量的代数性质:向量的以下代数性质适用于所有向量和标量;交换、关联、加性恒等式、加法逆、与向量分布、与标量分布以及与标量相关联。
- 线性组合:线性组合是由标量倍数 c₁v₁ + c₂v₂ + ... + cₐvₐ 之和定义的向量。砝码 c₁, c₂, ...Cₐ 可以是任何标量,包括零。
- 向量跨度:向量 v₁、v₂、...vₐ 表示为 Span{v₁, v₂, ...vₐ} 并且是可以写为 C₁v₁ + C₂v₂ + ... + CₐVₐ 的向量集合。
参考资料
¹引用自 Algebraic Properties of Vectors 向量的代数性质
²线性组合的定义,参考自《线性代数及其应用》第6版,作者:David C. Lay、Steven R. Lay和Judi J. McDonald。
³跨度的定义引用自David C. Lay,Steven R. Lay和Judi J. McDonald的线性代数及其应用第6版。
*除非另有说明,否则所有图片均由作者创建。
相关文章:

线性代数3:矢量方程
一、前言 欢迎回到系列文章的第三篇文章,内容是线性代数的基础知识,线性代数是机器学习背后的基础数学。在我之前的文章中,我介绍了梯队矩阵形式。本文将介绍向量、跨度和线性组合,并将这些新想法与我们已经学到的内容联系起来。本…...

线性代数的本质笔记
课程来自b站发现的《线性代数的本质》,可以帮助从直觉层面理解线性代数的一些基础概念,以及把一些看似不同的数学概念解释之后,发现其实有内在的关联。 这里只对部分内容做一个记录,完整内容请自行观看视频~ 01-向量究竟是什么 …...
[SQL | MyBatis] MyBatis 简介
目录 一、MyBatis 简介 1、MyBatis 简介 2、工作流程 二、入门案例 1、准备工作 2、示例 三、Mapper 代理开发 1、问题简介 2、工作流程 3、注意事项 4、测试 四、核心配置文件 mybatis-config.xml 1、environment 2、typeAilases 五、基于 xml 的查询操作 1、…...
FreeRTOS介绍 和 将FreeRTOS移植到STM32F103C8T6
一、FreeRTOS 介绍 什么是 FreeRTOS ? Free即免费的,RTOS的全称是Real time operating system,中文就是实时操作系统。 注意:RTOS不是指某一个确定的系统,而是指一类操作系统。比如:uc/OS,Fr…...

zookeeper(目前只有安装)
安装 流程 学kafka的时候安装 Apache ZooKeeper 安装地址:https://archive.apache.org/dist/zookeeper/zookeeper-3.5.7/apache-zookeeper-3.5.7-bin.tar.gz 解压 tar -zxvf kafka_2.12-3.0.0.tgz -C /export/server/ 改配置 cd config cp zoo_sample.cfg z…...
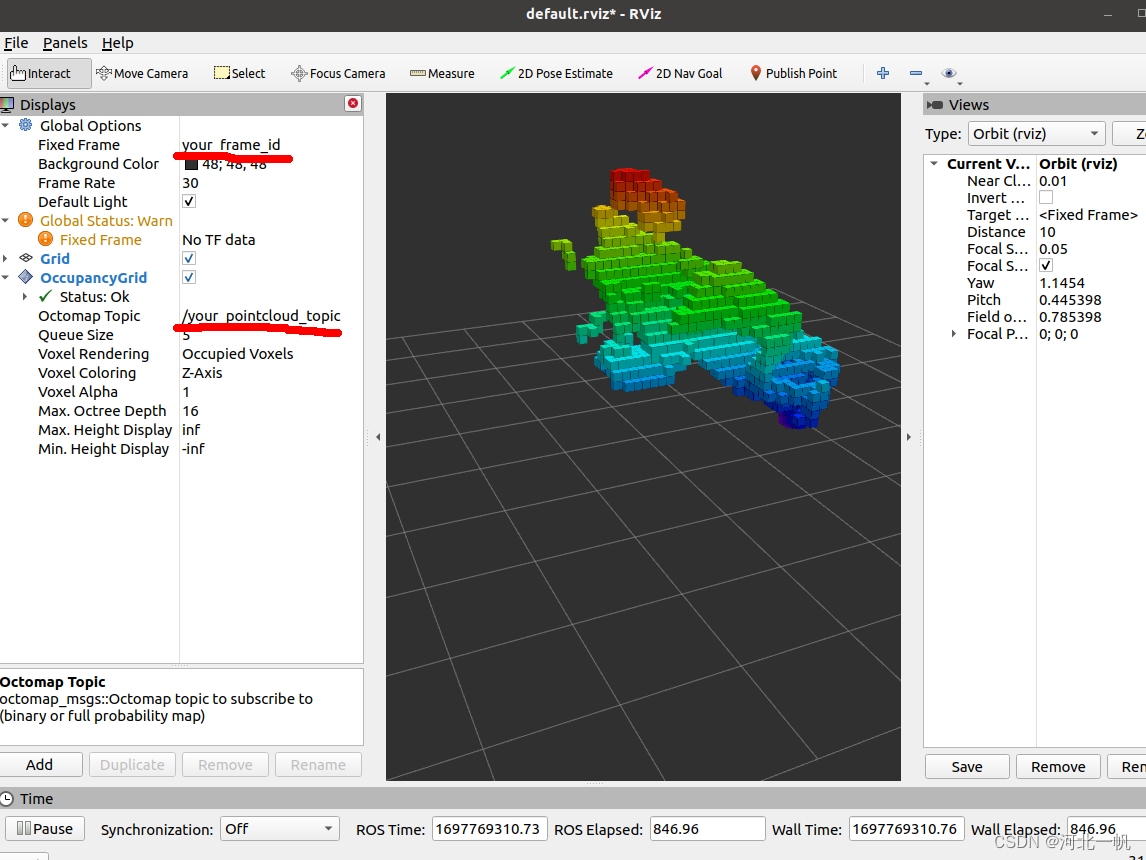
点云cloudpoint生成octomap的OcTree的两种方法以及rviz可视化
第一种:在自己的项目中将点云通过ros的topic发布,用octomap_server订阅点云消息,在octomap_server中生成ocTree 再用rviz进行可视化。 创建工作空间,记得source mkdir temp_ocotmap_test/src cd temp_ocotmap_test catkin_make…...
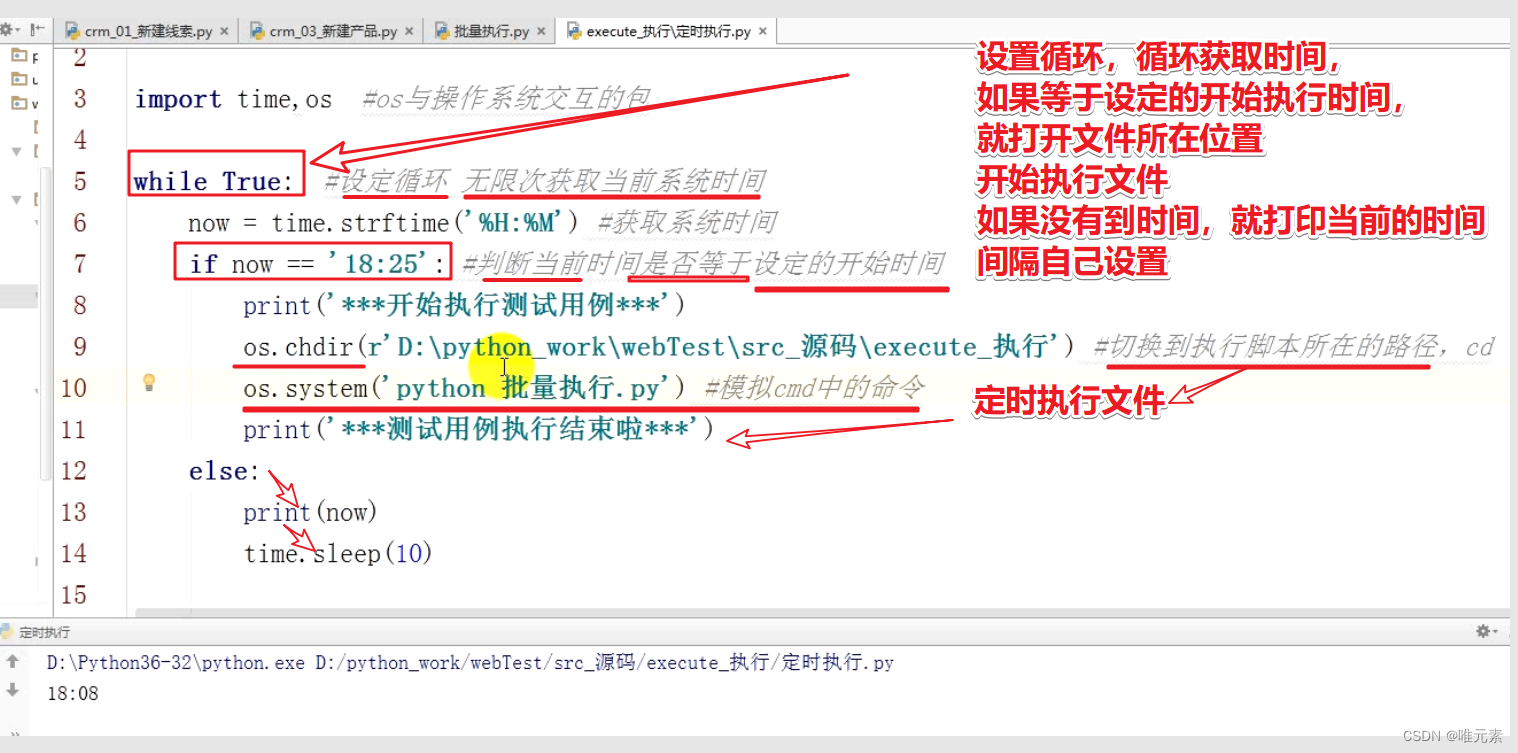
Python---死循环概念---while True
在编程中一个靠自身控制无法终止的程序称为“死循环”。 在Python中,我们也可以使用while True来模拟死循环: 代码: while True: print(每天进步一点点) 图示 应用: 比如,在测试里面,自动化测试用例…...
)
ElasticSearch容器化从0到1实践(问题汇总)
文章目录 ik插件如何安装?6.8.0版本JVM参数调整 ik插件如何安装? ik插件(中文分词插件)无法直接通过install指定插件名称的方式进行安装,可以通过指定zip包的方式对插件进行安装,需要注意的是通过zip包方式…...
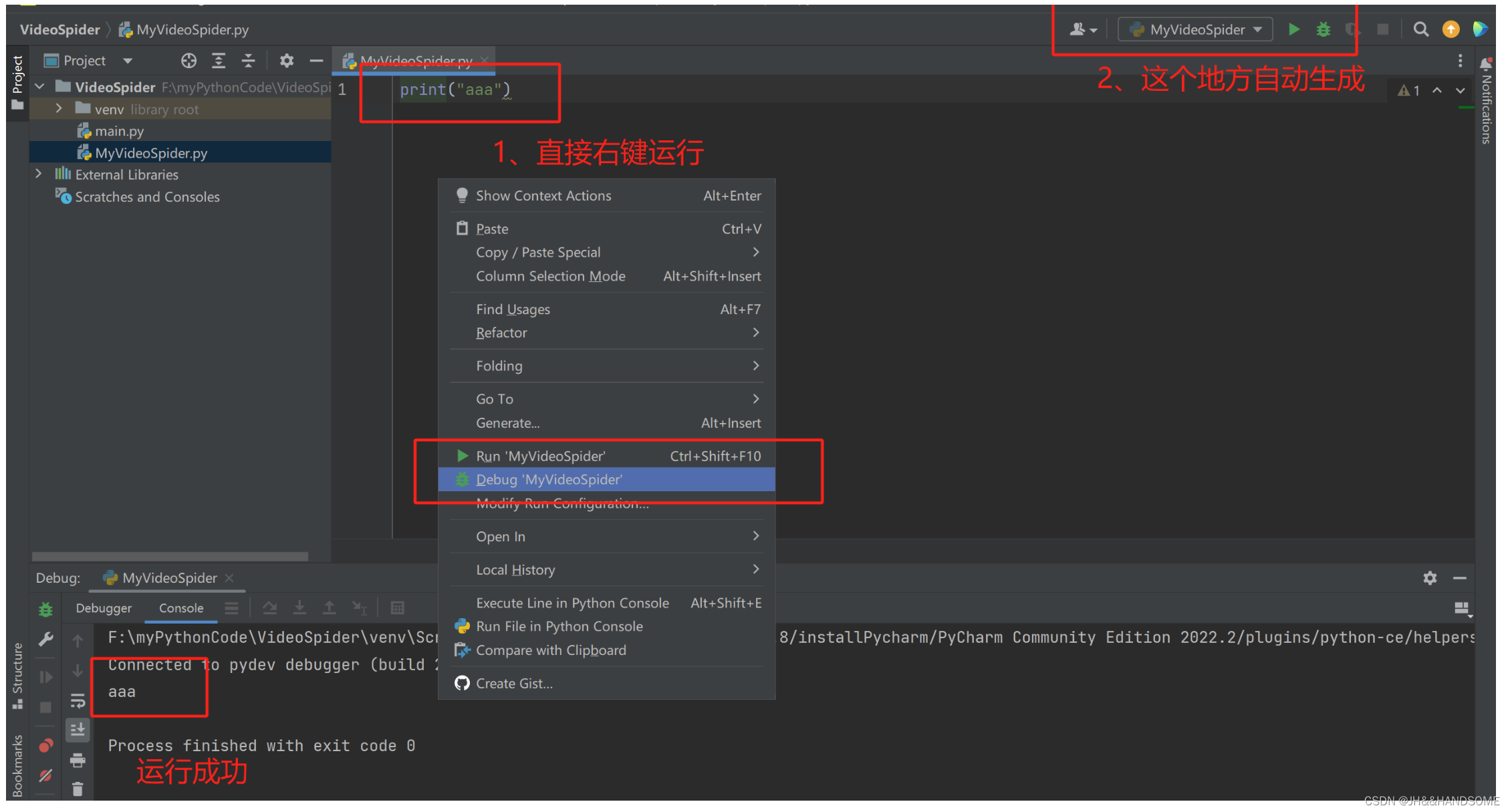
01、Python 安装 ,Pycharm 安装
目录 安装安装 Python安装 Pycharm 创建项目简单添加文件运行 简单爬取下载小视频 安装 python-3.8.10-amd64.exe – 先安装这个 pycharm-community-2022.2.exe 再安装这个 安装 Python python-3.8.10-amd64.exe 安装(这个是其他版本的安装,步骤一样…...
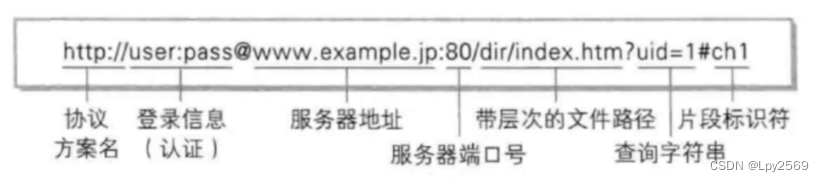
从输入URL到展示出页面
目录 了解URL 1. 输入URL 2. 域名解析 3. 建立连接 4. 服务器处理请求: 5. 返回响应: 6. 浏览器解析HTML: 7. 加载资源: 8. 渲染页面: 9. 执行JavaScript: 10. 页面展示: 从输入URL到…...

【C++】哈希的应用 -- 位图
文章目录 一、位图的概念二、位图的实现三、库中的 bitset四、位图的应用五、哈希切割 一、位图的概念 我们以一道面试题来引入位图的概念: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中 我…...
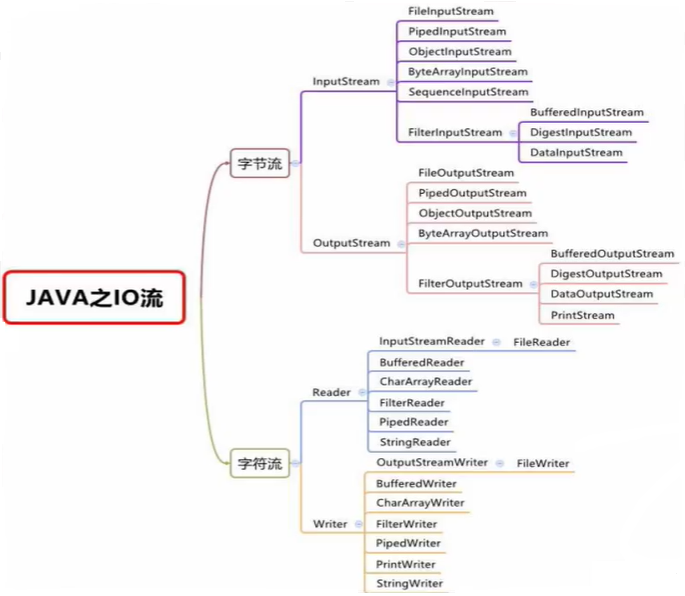
系列二、IO流原理及流的分类
一、概述 IO是Input、Output的缩写,IO流技术是非常实用的技术,用于处理数据传输,例如读写文件,网络通讯等。在Java程序中,对于数据的输入/输出操作以"流(stream)"的方式进行ÿ…...

【算法教程】排列与组合的实现
数据准备 在讲排列与组合之前,我们先定义数据元素类型Fruit class Fruit{constructor(name,price){this.name namethis.price price} }排列 对N个不同元素进行排序,总共有多少不同的排列方式? Step1: 从N个元素中取1个,共N种…...

uniapp实现简单的九宫格抽奖(附源码)
效果展示 uniapp实现大转盘抽奖 实现步骤: 1.该页面可设置8个奖品,每个奖品可设置中奖机会的权重,如下chance越大,中奖概率越高(大于0) // 示例代码 prizeList: [{id: 1,image: "https://img.alicdn…...
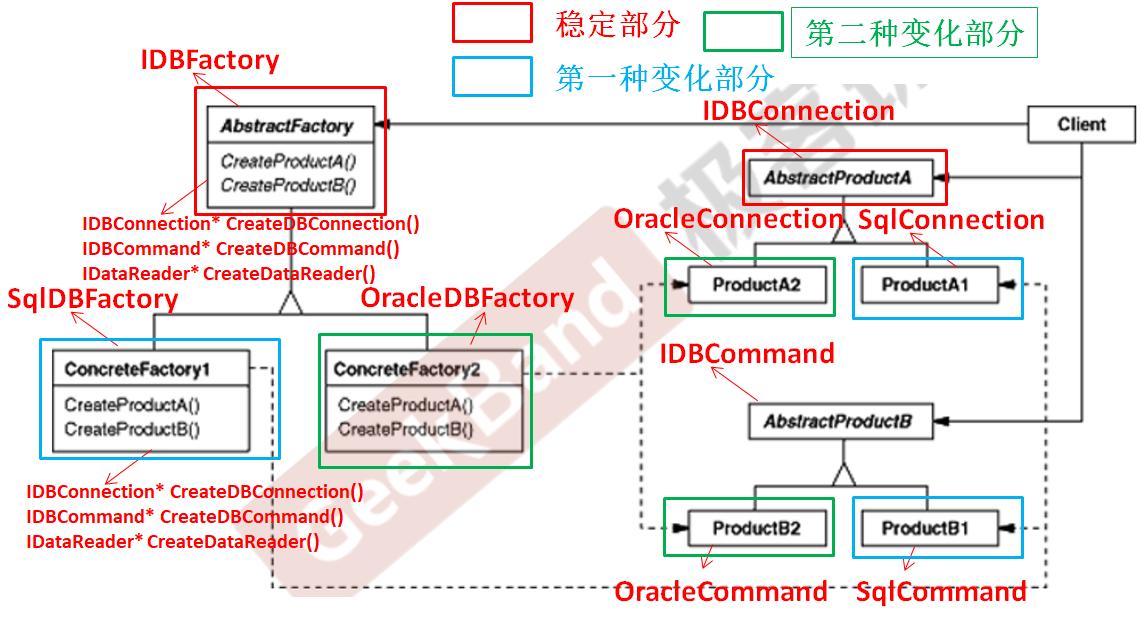
C++设计模式_09_Abstract Factory 抽象工厂
与上篇介绍的Factory Method工厂方法模式一样,Abstract Factory 抽象工厂模式也属于典型的“对象创建模式”模式,解决的问题也极其相似,在理解了Factory Method工厂方法模式的基础上再去理解Abstract Factory 抽象工厂模式就会变得更加容易。…...
一些前端面试思考
回流和重绘 先牢记这句话,回流必将引起重绘,而重绘不一定会引起回流。回流的代价要远大于重绘。 当你给一个元素更换颜色,这样的行为是不会影响页面布局的,DOM树不会变化,但颜色变了,渲染树得重新渲染页面&…...
)
Spring MVC(上)
1、Spring MVC简介: MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体类Bean:专…...
ORACLE内存结构
内存体系结构 目录 内存体系结构 2.1自动内存管理 2.2自动SGA内存管理 2.3手动SGA内存管理 2.3.1数据库缓冲区 2.3.1.1保留池 2.3.1.2回收池 2.3.2共享池 2.3.2.1SQL查询结果和函数查询结果 2.3.2.2库缓存 2.3.2.3数据字典缓存 2.3.3大池 2.3.4 …...

excel常用的几个函数
1、MID函数 通常用来返回返回指定字符串中的子串。 函数公式: MID(string, starting_at, extract_length) String(必填):包含要提取字符的文本字符串 starting_at(必填):文本中要提取的第一个字…...

【Bug】【内存相关】偶然发现一个内存溢出Bug复盘
一、问题 跑自动化用例的时候,uat-sg环境,发现SGW经常会返回 502 Bad Gateway响应 二、原因 经过SRE和BE Dev共同排查,502 是从ALB-- > 后端服务 后端服务无法响应导致,ALB会直接给客户端返回502。 服务端:由于c…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...
