数据结构预算法之买卖股票的最好时机(三)动态规划
目录:
一.题目
知识点:动态规划
二.动态规划数组思路确定
1.dp数组以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
一.题目



知识点:动态规划
动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果
二.动态规划数组思路
这道题目相对前面两道题目难了不少。
关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。
接来下我用动态规划五部曲详细分析一下:
确定dp数组以及下标的含义
一天一共就有五个状态,
(0)没有操作 (其实我们也可以不设置这个状态)
(1)第一次持有股票
(2)第一次不持有股票
(3)第二次持有股票
(4)第二次不持有股票
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
需要注意:dp[i][1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。
例如 dp[i][1] ,并不是说 第i天一定买入股票,有可能 第 i-1天 就买入了,那么 dp[i][1] 延续买入股票的这个状态。
2.确定递推公式
达到dp[i][1]状态,有两个具体操作:
操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i]
操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
那么dp[i][1]究竟选 dp[i-1][0] - prices[i],还是dp[i - 1][1]呢?
一定是选最大的,所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
同理dp[i][2]也有两个操作:
操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
同理可推出剩下状态部分:
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
3.dp数组如何初始化
第0天没有操作,这个最容易想到,就是0,即:dp[0][0] = 0;
第0天做第一次买入的操作,dp[0][1] = -prices[0];
第0天做第一次卖出的操作,这个初始值应该是多少呢?
此时还没有买入,怎么就卖出呢? 其实大家可以理解当天买入,当天卖出,所以dp[0][2] = 0;
第0天第二次买入操作,初始值应该是多少呢?应该不少同学疑惑,第一次还没买入呢,怎么初始化第二次买入呢?
第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后再买入一次(第二次买入),那么现在手头上没有现金,只要买入,现金就做相应的减少。
所以第二次买入操作,初始化为:dp[0][3] = -prices[0];
同理第二次卖出初始化dp[0][4] = 0;
4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
5.举例推导dp数组
以输入[1,2,3,4,5]为例

大家可以看到红色框为最后两次卖出的状态。
现在最大的时候一定是卖出的状态,而两次卖出的状态现金最大一定是最后一次卖出。如果想不明白的录友也可以这么理解:如果第一次卖出已经是最大值了,那么我们可以在当天立刻买入再立刻卖出。所以dp[4][4]已经包含了dp[4][2]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。
所以最终最大利润是dp[4][4]
以上五部都分析完了,不难写出如下代码:
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for (int i = 1; i < prices.size(); i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[prices.size() - 1][4];}
};时间复杂度:O(n)
空间复杂度:O(n × 5)
java实现
class Solution {public int maxProfit(int[] prices) {int len = prices.length;// 边界判断, 题目中 length >= 1, 所以可省去if (prices.length == 0) return 0;/** 定义 5 种状态:* 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出*/int[][] dp = new int[len][5];dp[0][1] = -prices[0];// 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润dp[0][3] = -prices[0];for (int i = 1; i < len; i++) {dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);dp[i][2] = Math.max(dp[i - 1][2], dp[i][1] + prices[i]);dp[i][3] = Math.max(dp[i - 1][3], dp[i][2] - prices[i]);dp[i][4] = Math.max(dp[i - 1][4], dp[i][3] + prices[i]);}return dp[len - 1][4];}
}相关文章:

数据结构预算法之买卖股票的最好时机(三)动态规划
目录:一.题目知识点:动态规划二.动态规划数组思路确定1.dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组一.题目知识点:动态规划动态规划算法的基本思想是:将待求解的问题分解成若干个相互联…...
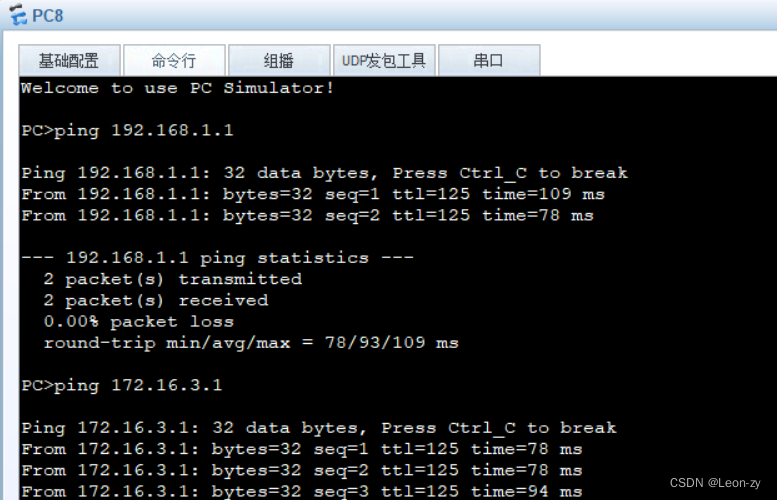
【数通网络交换基础梳理2】三层设备、网关、ARP表、VLAN、路由表及跨网段路由下一跳转发原理
一、不同网段如何通讯 同网段可以依靠二层交换机通讯,网络中存在多个网段192.168.1.1/24 172.16.1.1/24 173.73.1.1/24情况下如何互相通讯?上节留一下的问题,这节继续讲解。 1、这里以Ping命令讲解,PC1 ping173.73.1.2…...
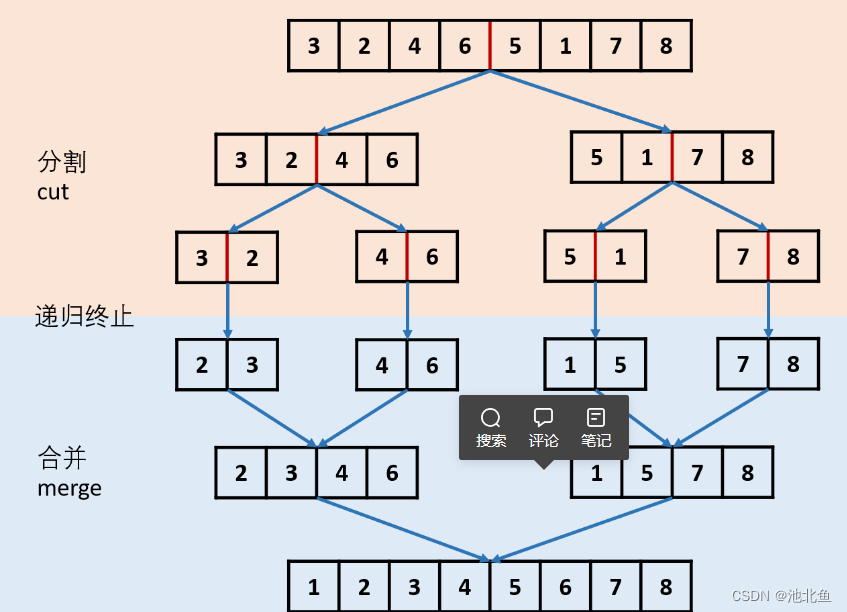
Java-排序链表问题
Java-排序链表问题题目题解方法:自顶向下归并排序算法题目 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 示例 1: 示例 2: 示例 3: 提示: *链表中节点的数目在范围 [0, 5 * 104]…...
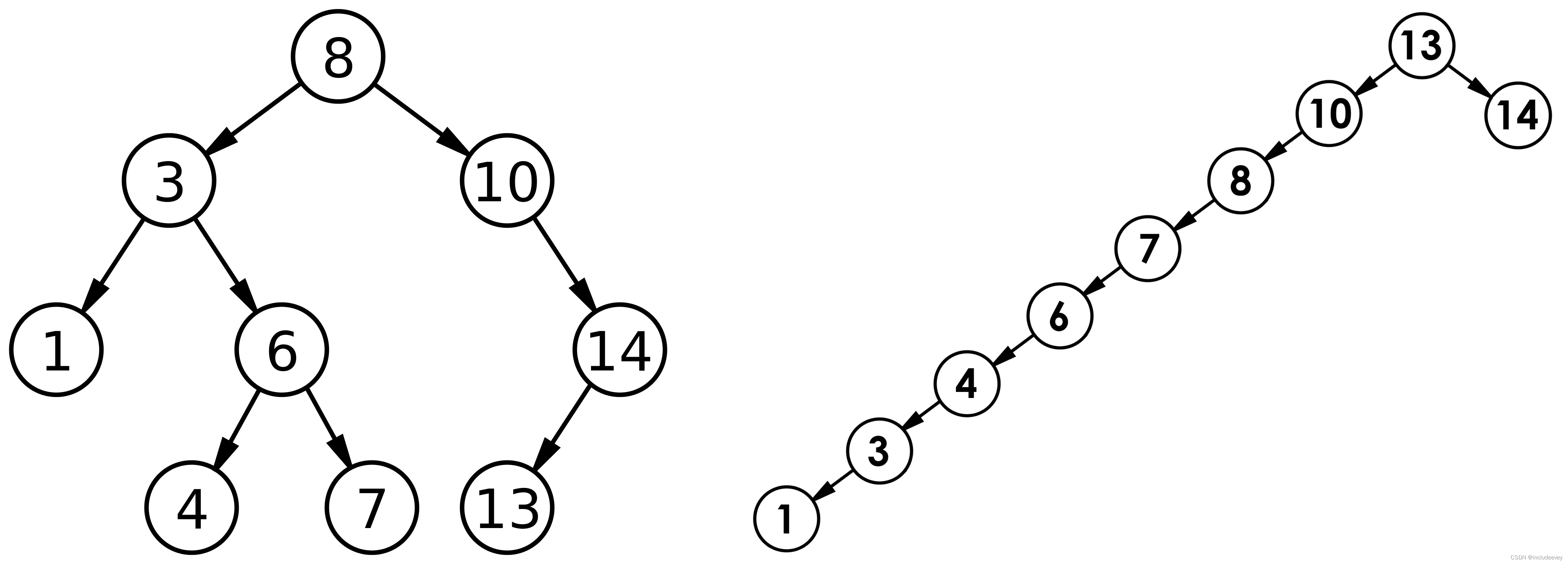
c++之二叉树【进阶版】
前言 在c语言阶段的数据结构系列中已经学习过二叉树,但是这篇文章是二叉树的进阶版,因为首先就会讲到一种树形结构“二叉搜索树”,学习二叉搜索树的目标是为了更好的理解map和set的特性。二叉搜索树的特性就是左子树键值小于根,右…...
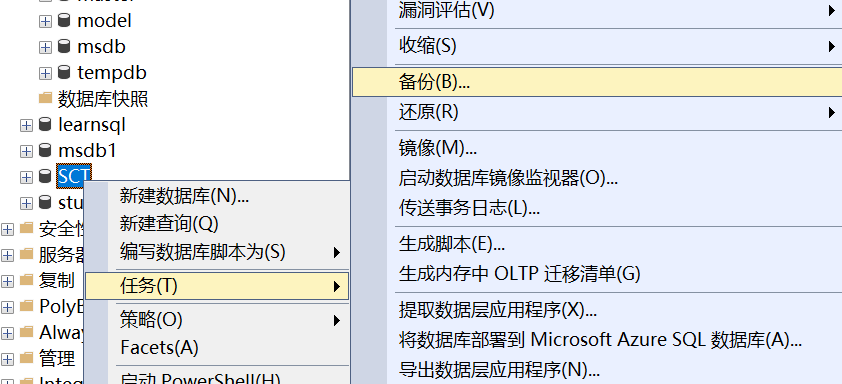
【数据库】 SQLServer
SQL Server 安装 配置 修改SQL Server默认的数据库文件保存路径_ 认识 master :是SQL Server中最重要的系统数据 库,存储SQL Server中的元数据。 Model:模板数据库,在创建新的数据库时,SQL Server 将会复制此数据…...

Linux 4.19 内核中 spinlock 概览
Linux内核中 spinlock相关数据结构和代码实现涉及的文件还是挺多的,这篇博客尝试从文件的角度来梳理一下 spinlock的相关数据结构和代码实现,适合想大概了解 Linux内核中 spinlock从上层 API到底层实现间的调用路径和传参变化,尤其适合了解 s…...
:基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错)
TensorFlow 1.x学习(系列二 :1):基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错
目录1.基本介绍2.图的结构3.会话,会话的run方法4.placeholder5.返回值异常写在前边的话:之前发布过一个关于TensorFlow1.x的转载系列,自己将基本的TensorFlow操作敲了一遍,但是仍然有很多地方理解的不够深入。所以重开一个系列&am…...
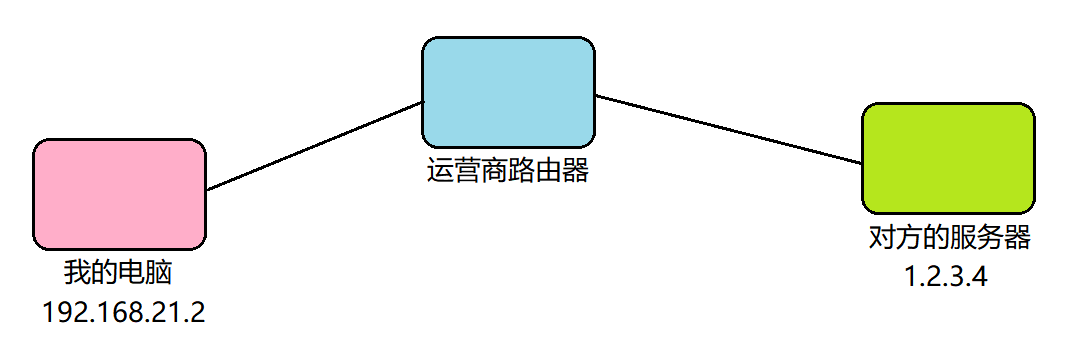
javaEE 初阶 — 关于 IPv4、IPv6 协议、NAT(网络地址转换)、动态分配 IP 地址 的介绍
文章目录1. IPv42. IPv63. NAT4. 动态分配 IP 地址1. IPv4 在互联网的世界中只有 0 和1 ,所以每个人都有一个由 0 和 1 组成的地址来让别人找到你。 这段由 0 和 1 组成的地址叫 IP 地址,这是互联网的基础资源,可以简单的理解为互联网的土地。…...
《Qt 6 C++开发指南》简介
我们编写的新书《Qt 6 C开发指南》在2月份终于正式发行销售了,这本书是对2018年5月出版的《Qt 5.9 C开发指南》的重磅升级。以下是本书前言的部分内容,算是对《Qt 6 C开发指南》的一个简介。1.编写本书的目的《Qt 5.9C开发指南》是我写的第一…...
CleanMyMac是什么清理软件?及使用教程
你知道CleanMyMac是什么吗?它的字面意思为“清理我的Mac”,作为软件,那就是一款Mac清理工具,Mac OS X 系统下知名系统清理软件,是数以万计的Mac用户的选择。它可以流畅地与系统性能相结合,只需简单的步骤就…...

Linux小黑板(9):共享内存
"My poor lost soul"上章花了不少的篇幅讲了讲基于管道((匿名、命名))技术实现的进程间通信。进程为什么需要通信?目的是为了完成进程间的"协同",提高处理数据的能力、优化业务逻辑的实现等等,在linux中我们已经谈过了一个通信的大类…...
Detr源码解读(mmdetection)
Detr源码解读(mmdetection) 1、原理简要介绍 整体流程: 在给定一张输入图像后,1)特征向量提取: 首先经过ResNet提取图像的最后一层特征图F。注意此处仅仅用了一层特征图,是因为后续计算复杂度原因,另外&am…...
一个.Net Core开发的,撑起月6亿PV开源监控解决方案
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 项目发布后,对于我们程序员来说,项目还不是真正的结束,保证项目的稳定运行也是非常重要的,而对于服务器的监控,就是保证稳定运行的手段之一。对数据库、…...
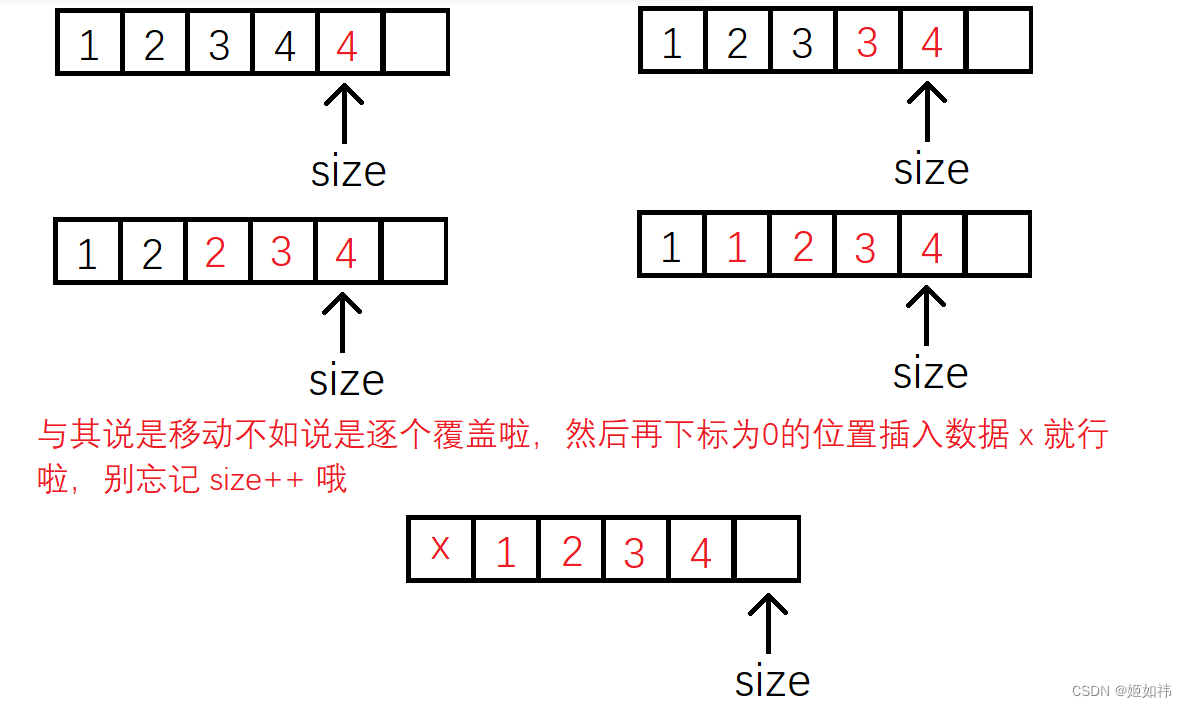
C语言数据结构初阶(2)----顺序表
目录 1. 顺序表的概念及结构 2. 动态顺序表的接口实现 2.1 SLInit(SL* ps) 的实现 2.2 SLDestory(SL* ps) 的实现 2.3 SLPrint(SL* ps) 的实现 2.4 SLCheckCapacity(SL* ps) 的实现 2.5 SLPushBack(SL* ps, SLDataType x) 的实现 2.6 SLPopBack(SL* ps) 的实现 2.7 SLP…...
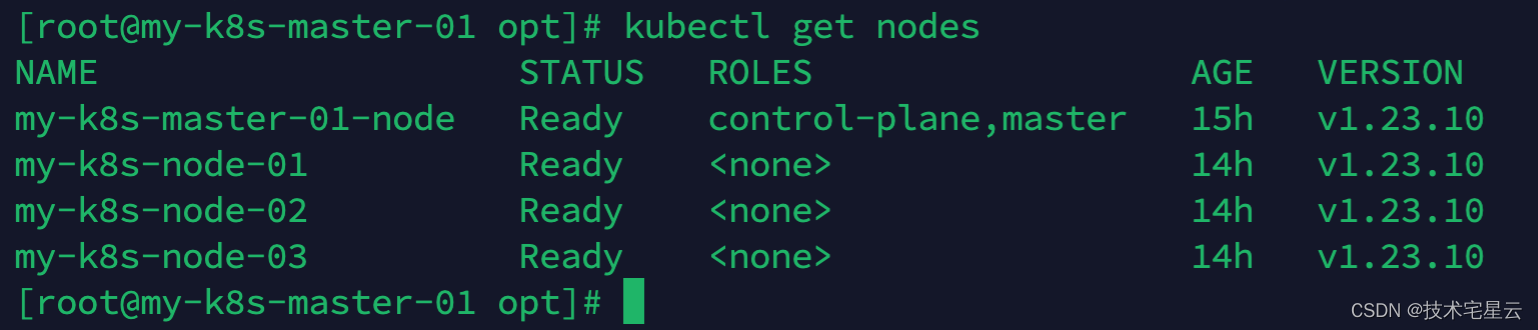
K8S常用命令速查手册
K8S常用命令速查手册一. K8S日常维护常用命令1.1 查看kubectl版本1.2 启动kubelet1.3 master节点执行查看所有的work-node节点列表1.4 查看所有的pod1.5 检查kubelet运行状态排查问题1.6 诊断某pod故障1.7 诊断kubelet故障方式一1.8 诊断kubelet故障方式二二. 端口策略相关2.1 …...

Linux系统下命令行安装MySQL5.6+详细步骤
1、因为想在腾讯云的服务器上创建自己的数据库,所以我在这里是通过使用Xshell 7来连接腾讯云的远程服务器; 2、Xshell 7与服务器连接好之后,就可以开始进行数据库的安装了(如果服务器曾经安装过数据库,得将之前安装的…...
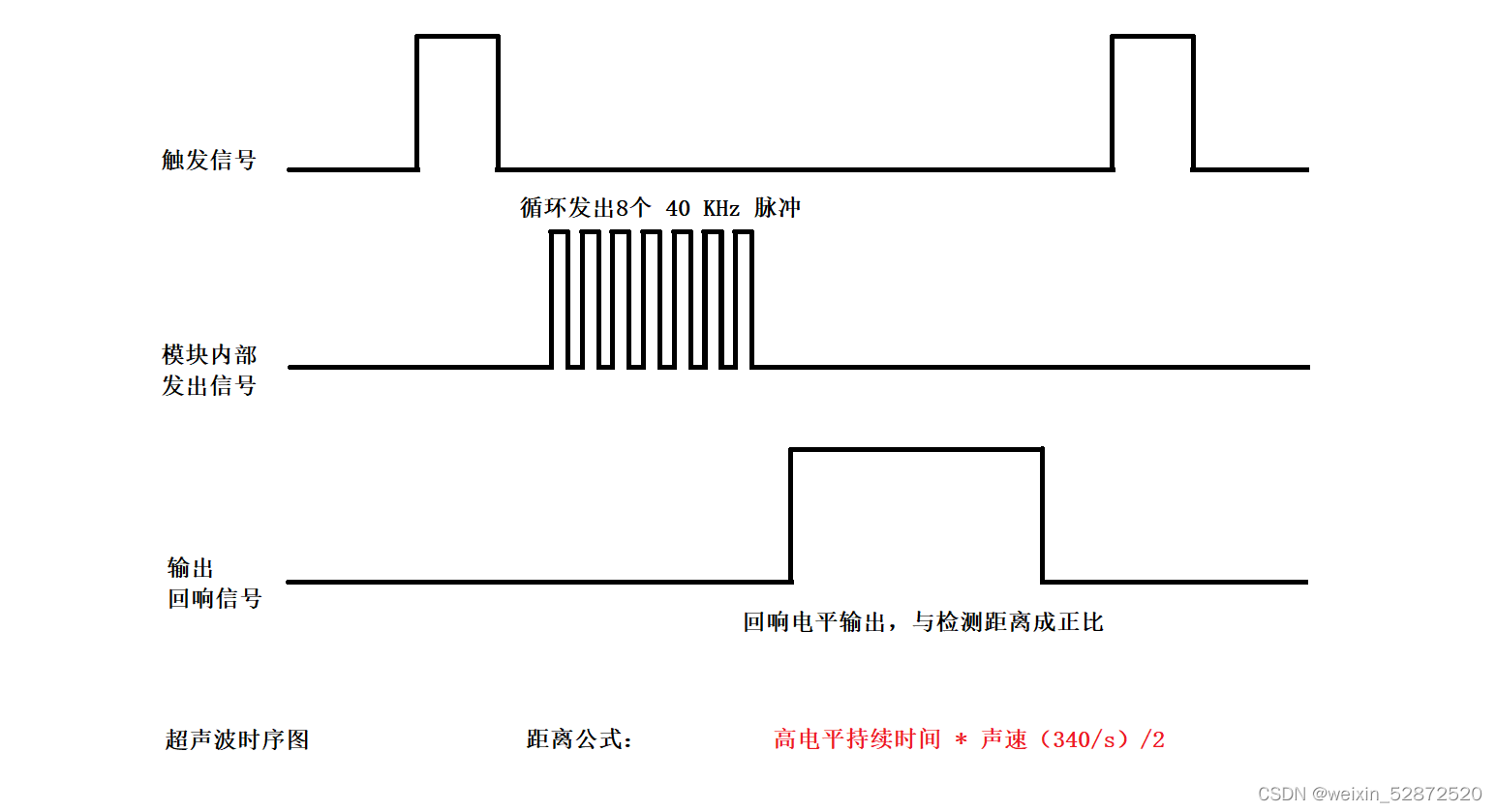
13.STM32超声波模块讲解与实战
目录 1.超声波模块讲解 2.超声波时序图 3.超声波测距步骤 4.项目实战 1.超声波模块讲解 超声波传感器模块上面通常有两个超声波元器件,一个用于发射,一个用于接收。电路板上有4个引脚:VCC GND Trig(触发)ÿ…...

逆向之Windows PE结构
写在前面 对于Windows PE文件结构,个人认为还是非常有必要掌握和了解的,不管是在做逆向分析、免杀、病毒分析,脱壳加壳都是有着非常重要的技能。但是PE文件的学习又是一个非常枯燥过程,希望本文可以帮你有一个了解。 PE文件结构…...

ACL是什么
目录 一、ACL是什么 二、ACL的使用:setacl与getacl 1)针对特定使用者的方式: 1. 创建acl_test1后设置其权限 2. 读取acl_test1的权限 2)针对特定群组的方式: 3)针对有效权限 mask 的设置方式…...
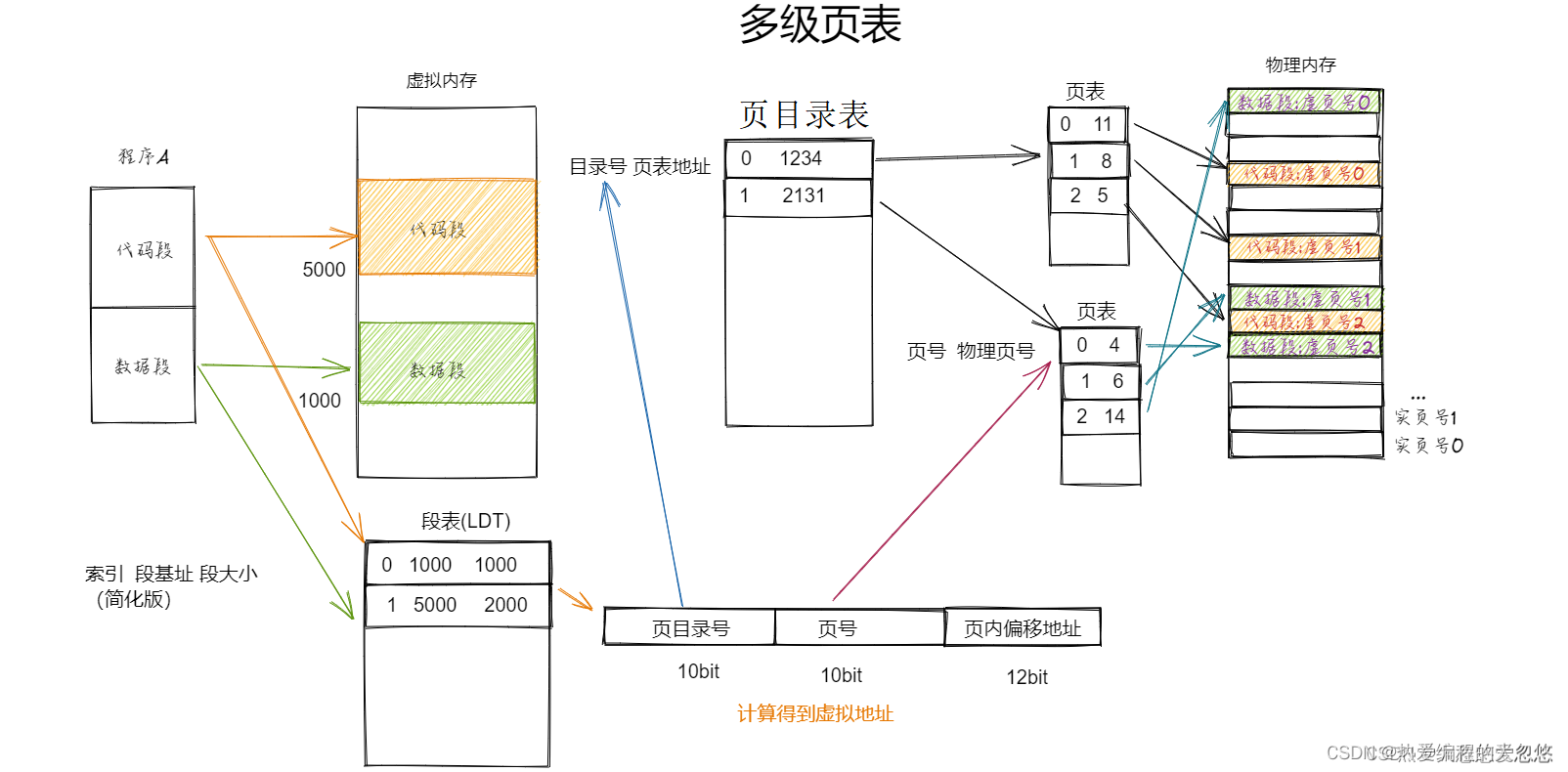
操作系统核心知识点整理--内存篇
操作系统核心知识点整理--内存篇按段对内存进行管理内存分区内存分页为什么需要多级页表TLB解决了多级页表什么样的缺陷?TLB缓存命中率高的原理是什么?段页结合: 为什么需要虚拟内存?虚拟地址到物理地址的转换过程段页式管理下程序如何载入内存?页面置…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
