Verilog 逻辑与()、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别
逻辑与(&&)
逻辑与是一个双目运算符,当符号两边为1时输出1,符号两边为0时输出0。
真值表:
&& | 0 | 1 | x | z |
0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | x | x |
x | 0 | x | x | x |
z | 0 | x | x | x |
两个4bit的数字相与;A=4'b0x1z;B=4'b01xx;C=4'b00xz;求A&&B;A&&C;是什么值?当逻辑与&&操作符两边的数字均含有“1”,则输出1。
那么怎么判断A、B、C为是否含有“1”呢。当A为0的时候,A等于4'b0,即每位都为0,即只需A的4位矢量之间做一下“逻辑或”运算,A[3] || A[2] || A[1] || A[0],也可写成(|A);当4位矢量中只需有一位为1,那么A就含有“1”。即哪怕A中具有不定态x或者高阻态z,A = 4'b0x1z在逻辑与的判断下会判定为“1”。
故 A && B = 4'b0x1z && 4'b01xx = 1
C = 4'b00xz,其中没有bit位为1,所以在逻辑与的眼中,C为“1”,进而有:
A && C = 4'b0x1z && 4'b00xz = 0
按位与(&)
按位与有两种使用方式,一种是双目操作,即一个操作符对应两个操作数A&B;另一种是单目操作,即一个操作符对应一个操作数&A。
双目操作
一个4bit的数和一个4bit的数按位与的结果还是一个4bit数,例如A[3:0] & B[3:0] = { A[3] && B[3] , A[2] && B[2], A[1] && B[1], A[0] && B[0] }
假设A = 4'b10xz;B = 4'b0011;C = 4'bz011;
A & B = 4'b00xx;A & C =4'bx0xx;
单目操作
一个4bit的数对自己进行按位与,输出的结果为1bit的数。
假设A = 4'b10xz;B = 4'b0011;
& A = A[3] && A[2] && A[1] && A[0] = 0
& B = 0
因为4bit数A和B中间都有0,所以A、B按位与结果都为0。
若C = 4'b11xz;则 & C = x
逻辑或(||)
逻辑或是一个双目运算符,当符号两边有1时输出1,符号两边全0时输出0。
|| | 0 | 1 | x | z |
0 | 0 | 1 | x | x |
1 | 1 | 1 | 1 | 1 |
x | x | 1 | x | x |
z | x | 1 | x | x |
两个4bit的数字相与;A=4'b0x1z;B=4'b01xx;C=4'b00xz;求A&&B;A&&C;是什么值?当逻辑与&&操作符两边的有数字含有“1”,则输出1。
当4位矢量中只需有一位为1,那么A就含有“1”。即哪怕A中具有不定态x或者高阻态z,A = 4'b0x1z在逻辑与的判断下会判定为“1”。
所以A || B = 1;A || C = 1
按位或(|)
同按位与一样,按位或也有两种使用方式,一种是双目操作,即一个操作符对应两个操作数A|B;另一种是单目操作,即一个操作符对应一个操作数|A。
双目操作
一个4bit的数和一个4bit的数按位或的结果还是一个4bit数,例如A[3:0] & B[3:0] = { A[3] || B[3] , A[2] || B[2], A[1] || B[1], A[0] || B[0] }
假设A = 4'b10xz;B = 4'b0011;C = 4'bz011;
A | B = 4'b10xz | 4'b0011 = 4'b1011;
A | C = 4'b10xz | 4'bz011 = 4'b1011;
单目操作
一个4bit的数对自己进行按位或,输出的结果为1bit的数。
假设A = 4'b10xz;B = 4'b0011;
| A = A[3] || A[2] || A[1] || A[0] = 1
| B = 1
因为4bit数A和B中间都有1,所以A、B按位或结果都为1。
若C = 4'b00xz;则 | C = x
相等运算符(==)
参与比较的两个操作数必须逐位相等,其相等比较的结果才为 1, 如果某些位是不定态或高阻值,其相等比较得到的结果是不定值。
相等运算符的比较,只要等式的两端有x或者高阻态z出现,那么结果就是一定是x,譬如:
(4'b1010 == 4'b101x)= x
(4'b101z == 4'b1010)= x
(4'b10x1 == 4'b10x1)= x
(4'b1011 == 4'b1011)= 1
(4'b1010 == 4'b1011)= 0
全等运算符(===)
全等比较是对这些不定态或高阻值的位也进行比较,两个操作数必须完全一致,其结果才是 1,否则结果是 0。
(4'b1010 === 4'b101x)= 0
(4'b101z === 4'b1010)= 0
(4'b101z === 4'b101z)= 1
(4'b101x === 4'b101x)= 1
相等运算符和全等运算符的真值表
== | 0 | 1 | x | z | === | 0 | 1 | x | z |
0 | 1 | 0 | x | x | 0 | 1 | 0 | 0 | 0 |
1 | 0 | 1 | x | x | 1 | 0 | 1 | 0 | 0 |
x | x | x | x | x | x | 0 | 0 | 1 | 0 |
z | x | x | x | x | z | 0 | 0 | 0 | 1 |
相关文章:
、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别)
Verilog 逻辑与()、按位与()、逻辑或(||)、按位或(|)、等于(==)、全等(===)的区别
逻辑与(&&)逻辑与是一个双目运算符,当符号两边为1时输出1,符号两边为0时输出0。真值表:&&01xz00000101xxx0xxxz0xxx两个4bit的数字相与;A4b0x1z;B4b01xx;C4b00xz&am…...

剑指 Offer 22. 链表中倒数第k个节点
剑指 Offer 22. 链表中倒数第k个节点 难度:easy\color{Green}{easy}easy 题目描述 输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。 例如,一个链…...

数据结构预算法之买卖股票的最好时机(三)动态规划
目录:一.题目知识点:动态规划二.动态规划数组思路确定1.dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组一.题目知识点:动态规划动态规划算法的基本思想是:将待求解的问题分解成若干个相互联…...
【数通网络交换基础梳理2】三层设备、网关、ARP表、VLAN、路由表及跨网段路由下一跳转发原理
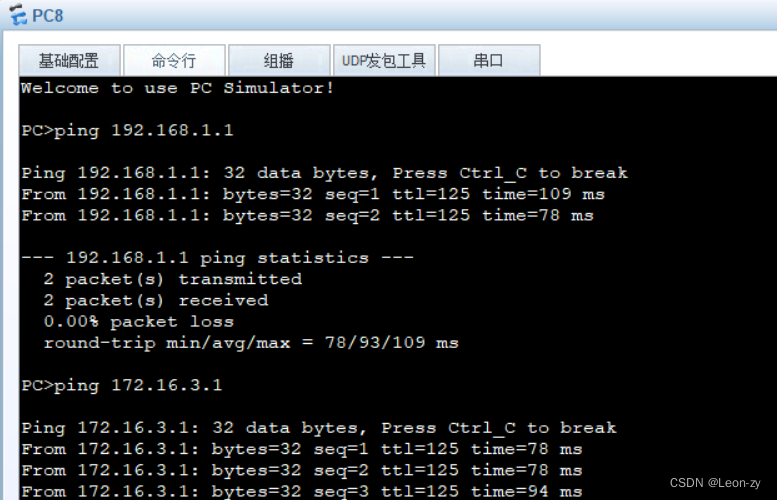
一、不同网段如何通讯 同网段可以依靠二层交换机通讯,网络中存在多个网段192.168.1.1/24 172.16.1.1/24 173.73.1.1/24情况下如何互相通讯?上节留一下的问题,这节继续讲解。 1、这里以Ping命令讲解,PC1 ping173.73.1.2…...
Java-排序链表问题
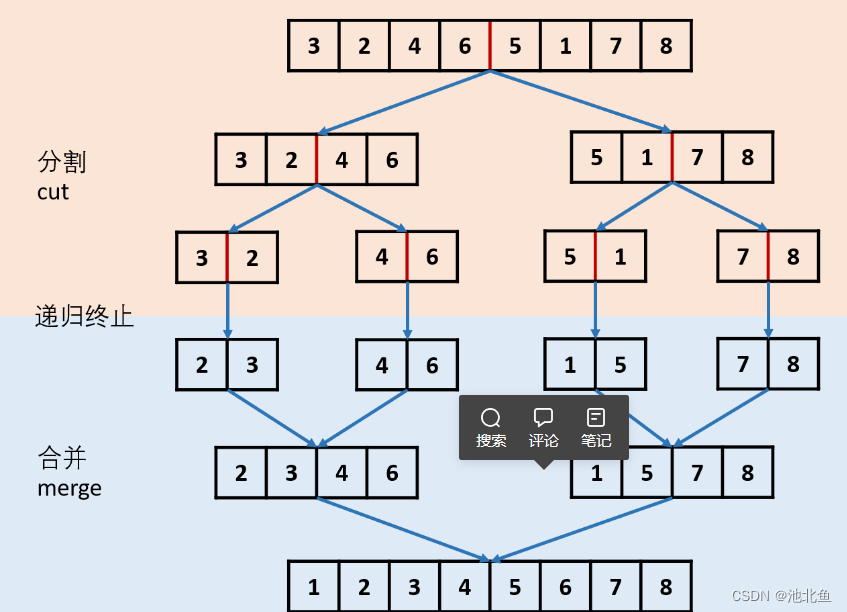
Java-排序链表问题题目题解方法:自顶向下归并排序算法题目 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 示例 1: 示例 2: 示例 3: 提示: *链表中节点的数目在范围 [0, 5 * 104]…...
c++之二叉树【进阶版】
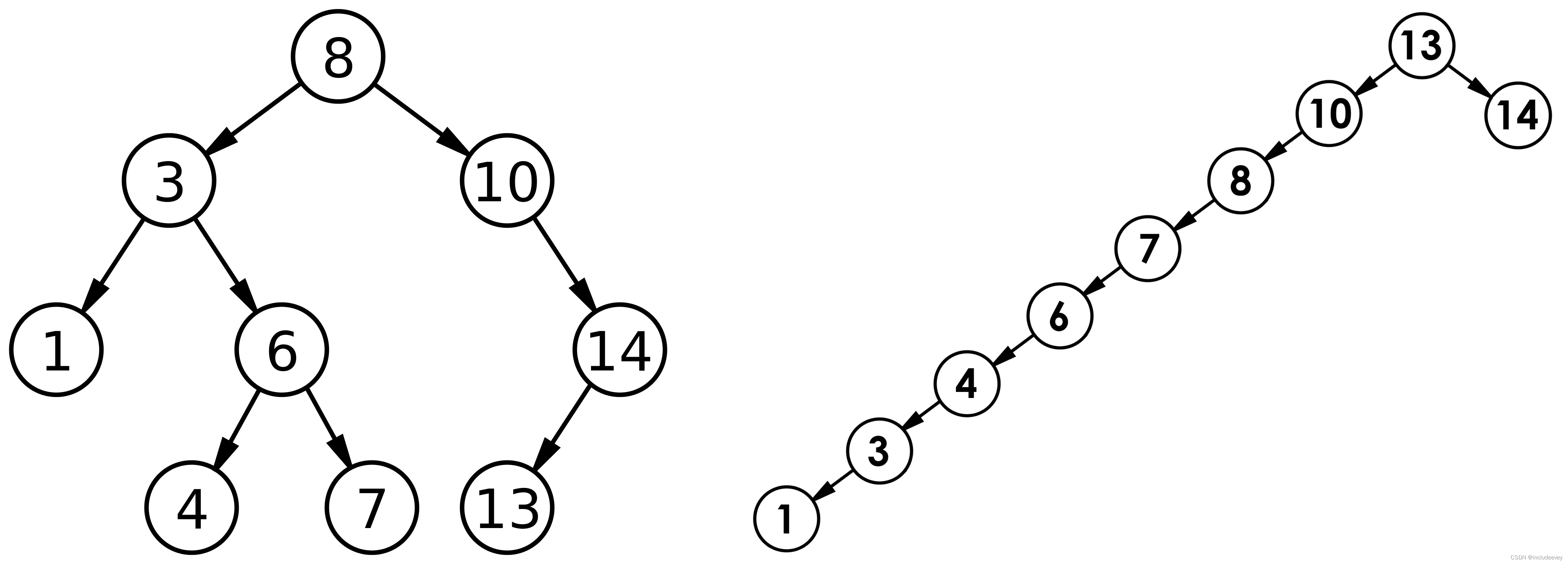
前言 在c语言阶段的数据结构系列中已经学习过二叉树,但是这篇文章是二叉树的进阶版,因为首先就会讲到一种树形结构“二叉搜索树”,学习二叉搜索树的目标是为了更好的理解map和set的特性。二叉搜索树的特性就是左子树键值小于根,右…...
【数据库】 SQLServer
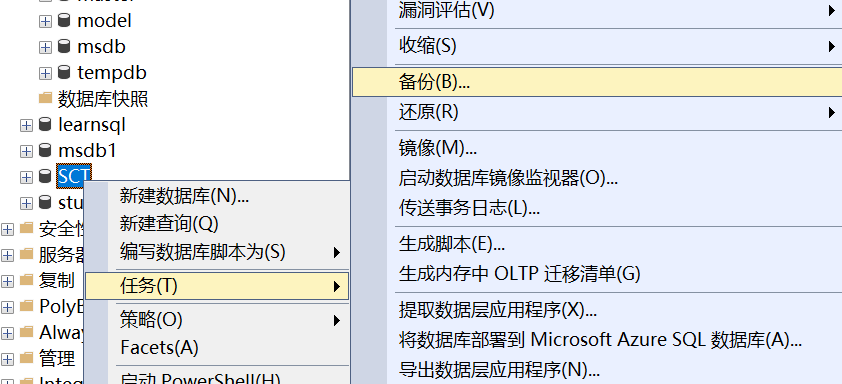
SQL Server 安装 配置 修改SQL Server默认的数据库文件保存路径_ 认识 master :是SQL Server中最重要的系统数据 库,存储SQL Server中的元数据。 Model:模板数据库,在创建新的数据库时,SQL Server 将会复制此数据…...

Linux 4.19 内核中 spinlock 概览
Linux内核中 spinlock相关数据结构和代码实现涉及的文件还是挺多的,这篇博客尝试从文件的角度来梳理一下 spinlock的相关数据结构和代码实现,适合想大概了解 Linux内核中 spinlock从上层 API到底层实现间的调用路径和传参变化,尤其适合了解 s…...
:基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错)
TensorFlow 1.x学习(系列二 :1):基本概念TensorFlow的基本介绍,图,会话,会话中的run(),placeholder(),常见的报错
目录1.基本介绍2.图的结构3.会话,会话的run方法4.placeholder5.返回值异常写在前边的话:之前发布过一个关于TensorFlow1.x的转载系列,自己将基本的TensorFlow操作敲了一遍,但是仍然有很多地方理解的不够深入。所以重开一个系列&am…...
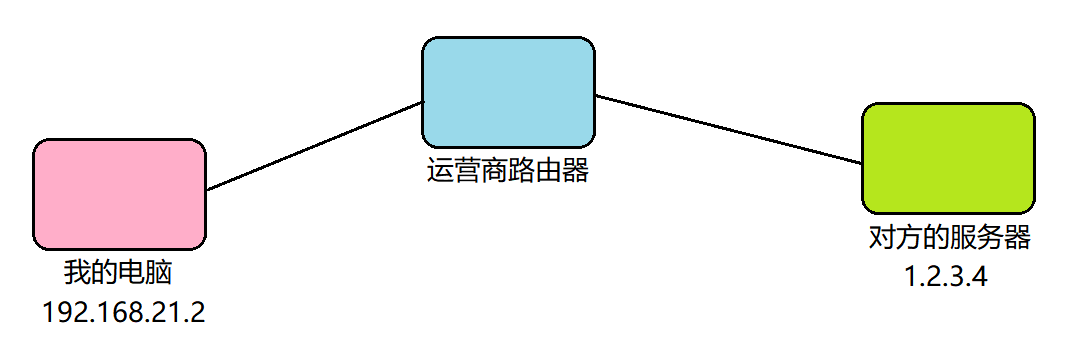
javaEE 初阶 — 关于 IPv4、IPv6 协议、NAT(网络地址转换)、动态分配 IP 地址 的介绍
文章目录1. IPv42. IPv63. NAT4. 动态分配 IP 地址1. IPv4 在互联网的世界中只有 0 和1 ,所以每个人都有一个由 0 和 1 组成的地址来让别人找到你。 这段由 0 和 1 组成的地址叫 IP 地址,这是互联网的基础资源,可以简单的理解为互联网的土地。…...
《Qt 6 C++开发指南》简介
我们编写的新书《Qt 6 C开发指南》在2月份终于正式发行销售了,这本书是对2018年5月出版的《Qt 5.9 C开发指南》的重磅升级。以下是本书前言的部分内容,算是对《Qt 6 C开发指南》的一个简介。1.编写本书的目的《Qt 5.9C开发指南》是我写的第一…...
CleanMyMac是什么清理软件?及使用教程
你知道CleanMyMac是什么吗?它的字面意思为“清理我的Mac”,作为软件,那就是一款Mac清理工具,Mac OS X 系统下知名系统清理软件,是数以万计的Mac用户的选择。它可以流畅地与系统性能相结合,只需简单的步骤就…...

Linux小黑板(9):共享内存
"My poor lost soul"上章花了不少的篇幅讲了讲基于管道((匿名、命名))技术实现的进程间通信。进程为什么需要通信?目的是为了完成进程间的"协同",提高处理数据的能力、优化业务逻辑的实现等等,在linux中我们已经谈过了一个通信的大类…...
Detr源码解读(mmdetection)
Detr源码解读(mmdetection) 1、原理简要介绍 整体流程: 在给定一张输入图像后,1)特征向量提取: 首先经过ResNet提取图像的最后一层特征图F。注意此处仅仅用了一层特征图,是因为后续计算复杂度原因,另外&am…...
一个.Net Core开发的,撑起月6亿PV开源监控解决方案
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 项目发布后,对于我们程序员来说,项目还不是真正的结束,保证项目的稳定运行也是非常重要的,而对于服务器的监控,就是保证稳定运行的手段之一。对数据库、…...
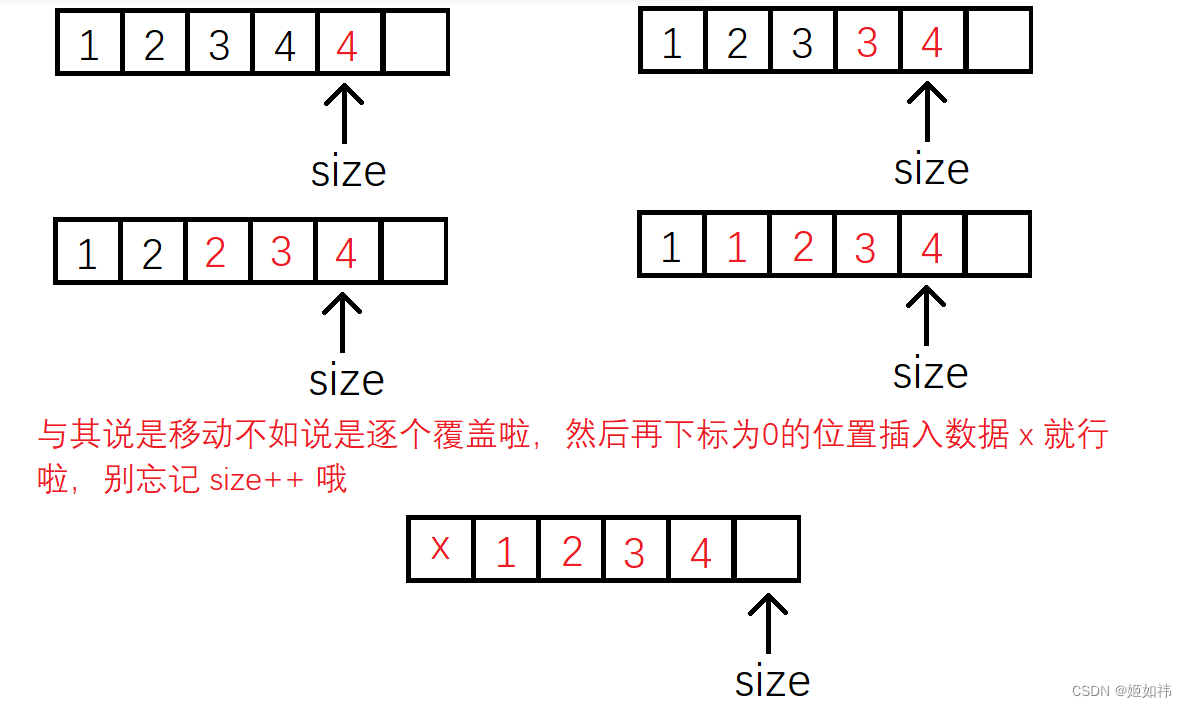
C语言数据结构初阶(2)----顺序表
目录 1. 顺序表的概念及结构 2. 动态顺序表的接口实现 2.1 SLInit(SL* ps) 的实现 2.2 SLDestory(SL* ps) 的实现 2.3 SLPrint(SL* ps) 的实现 2.4 SLCheckCapacity(SL* ps) 的实现 2.5 SLPushBack(SL* ps, SLDataType x) 的实现 2.6 SLPopBack(SL* ps) 的实现 2.7 SLP…...
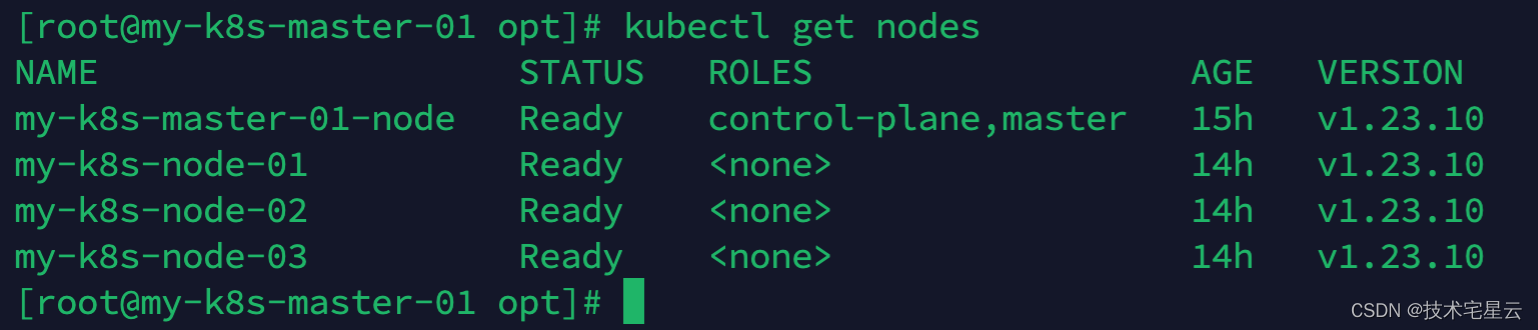
K8S常用命令速查手册
K8S常用命令速查手册一. K8S日常维护常用命令1.1 查看kubectl版本1.2 启动kubelet1.3 master节点执行查看所有的work-node节点列表1.4 查看所有的pod1.5 检查kubelet运行状态排查问题1.6 诊断某pod故障1.7 诊断kubelet故障方式一1.8 诊断kubelet故障方式二二. 端口策略相关2.1 …...

Linux系统下命令行安装MySQL5.6+详细步骤
1、因为想在腾讯云的服务器上创建自己的数据库,所以我在这里是通过使用Xshell 7来连接腾讯云的远程服务器; 2、Xshell 7与服务器连接好之后,就可以开始进行数据库的安装了(如果服务器曾经安装过数据库,得将之前安装的…...
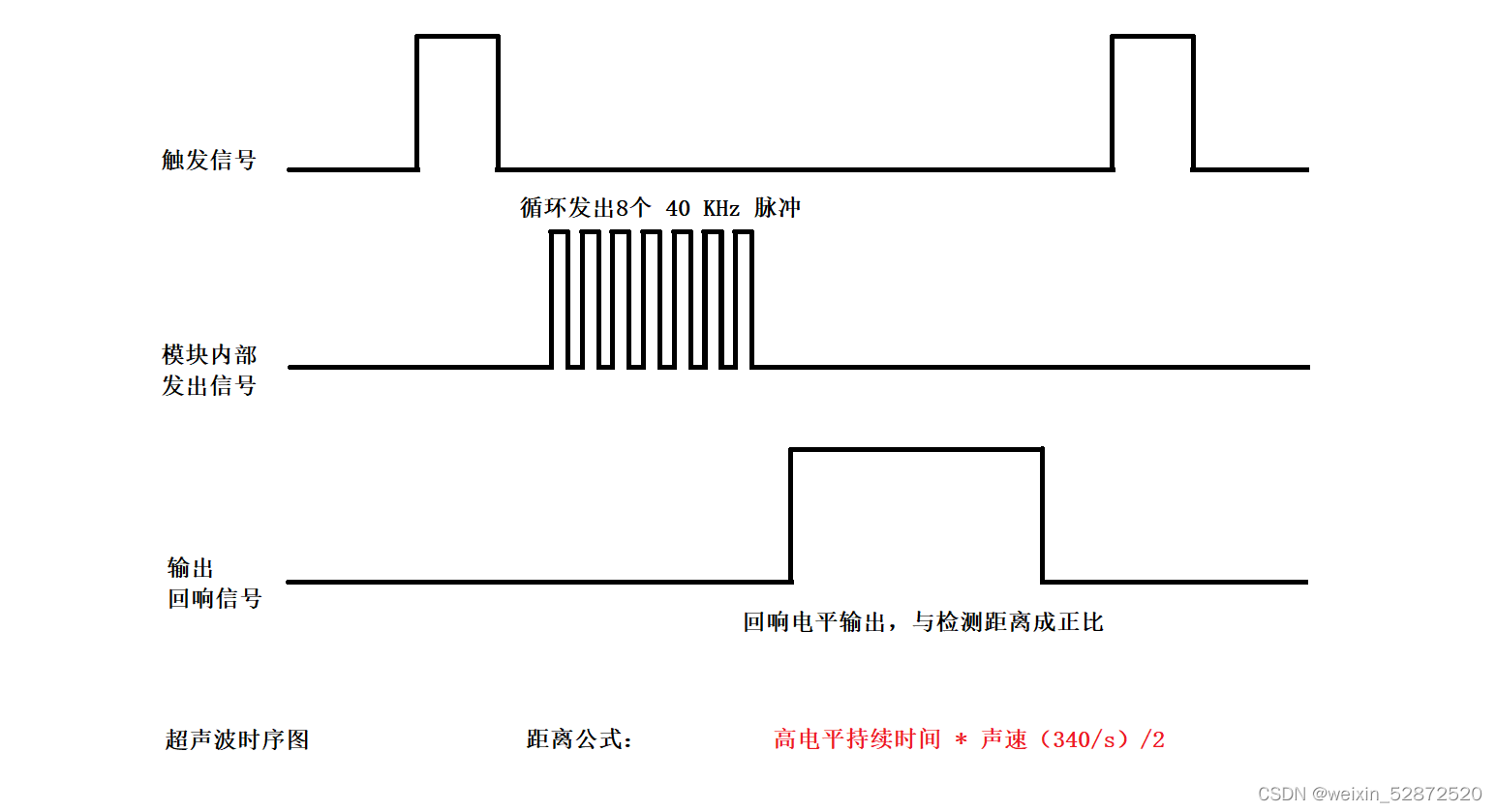
13.STM32超声波模块讲解与实战
目录 1.超声波模块讲解 2.超声波时序图 3.超声波测距步骤 4.项目实战 1.超声波模块讲解 超声波传感器模块上面通常有两个超声波元器件,一个用于发射,一个用于接收。电路板上有4个引脚:VCC GND Trig(触发)ÿ…...

逆向之Windows PE结构
写在前面 对于Windows PE文件结构,个人认为还是非常有必要掌握和了解的,不管是在做逆向分析、免杀、病毒分析,脱壳加壳都是有着非常重要的技能。但是PE文件的学习又是一个非常枯燥过程,希望本文可以帮你有一个了解。 PE文件结构…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
