当前位置： 首页 > news >正文

SLAM中相机姿态估计算法推导基础数学总结

news 2026/2/9 22:42:36

相机模型

基本模型

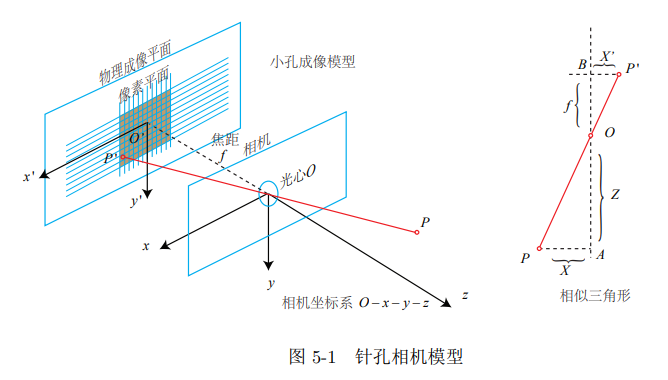
在这里插入图片描述
内参
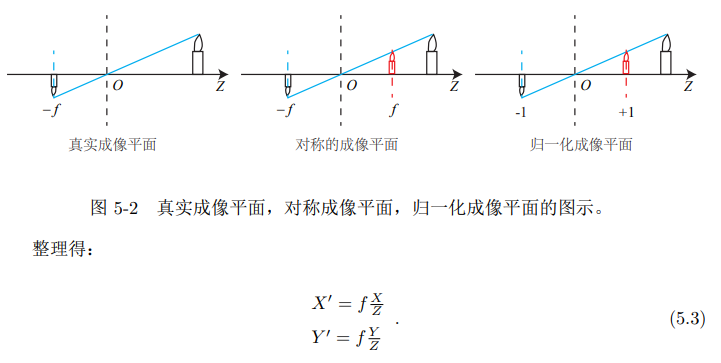
在这里插入图片描述
在这里插入图片描述
外参
在这里插入图片描述
在这里插入图片描述

对极几何

对极约束

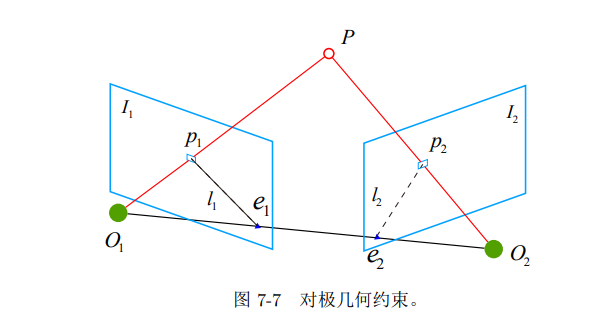
在这里插入图片描述
在这里插入图片描述
外积符号
在这里插入图片描述
基础矩阵F和本质矩阵E
在这里插入图片描述
在这里插入图片描述
相机姿态估计问题分为如下两步:

在这里插入图片描述

本质矩阵

E = t ∧ R E=t^{\wedge}R E=t∧R因为 t ∧ t^{\wedge} t∧其实就是个3x3的反对称矩阵，所以 E E E也是一个3x3的矩阵

用八点法估计E
在这里插入图片描述
在这里插入图片描述

零空间矩阵的讲解

要通过E获得R和t就需要进行 E E E的奇异值(SVD)分解
在这里插入图片描述在这里插入图片描述
带入之后的看相机的正深度，就只有第一种情况满足

单应矩阵

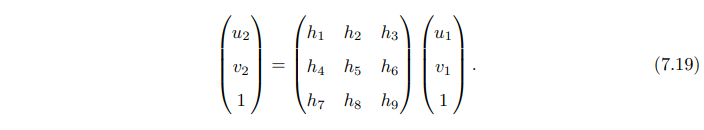
在这里插入图片描述
在这里插入图片描述

这个等式只有在非零因子情况下才成立，所以可以除以非零因子把 h 9 h_9 h9​变为0
在这里插入图片描述

三角测量

在这里插入图片描述在这里插入图片描述

3D-2D:PnP

直接线性变换

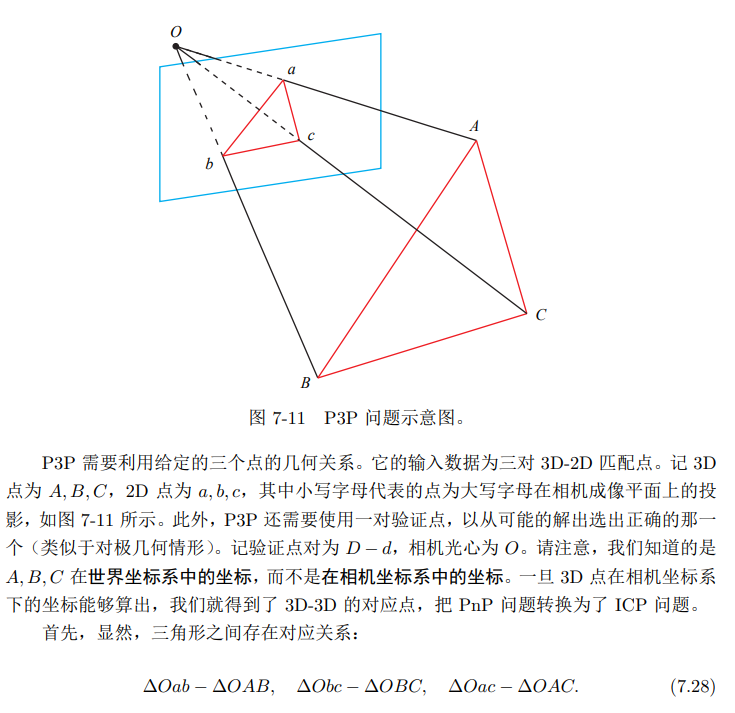
在这里插入图片描述

P3P

在这里插入图片描述
在这里插入图片描述
最后要求得未知量只有x,y,这是一个二元二次多项式方程，用吴消元法求解，最多得四个解，根据第四个点进行验证即可求得A，B,C 的3D坐标

Bundle Ajustment

在这里插入图片描述
这部分略显复杂，建议直接看视觉SLAM十四讲
在这里插入图片描述

相关文章：

SLAM中相机姿态估计算法推导基础数学总结

相机模型 基本模型 内参 外参 对极几何 对极约束 外积符号 基础矩阵F和本质矩阵E 相机姿态估计问题分为如下两步: 本质矩阵 E t ∧ R Et^{\wedge}R Et∧R因为 t ∧ t^{\wedge} t∧其实就是个3x3的反对称矩阵，所以 E E E也是一个3x3的矩阵 用八点法估计E…...

编程日记 2023/10/22 22:36:57

【RS】遥感影像/图片64位、16位（64bit、16bit）的意义和区别

在数字图像处理中，我们常常会听到不同的位数术语，比如64位、16位和8位（64bit、16bit、8bit）。这些位数指的是图像的深度，也就是图像中每个像素可以显示的颜色数。位数越高，图像可以显示的颜色数就越多&…...

编程日记 2023/10/22 22:35:55

【单元测试】--基础知识

一、什么是单元测试 单元测试是软件开发中的一种测试方法，用于验证代码中的单个组件（通常是函数、方法或类）是否按预期工作。它旨在隔离和测试代码的最小单元，以确保其功能正确，提高代码质量和可维护性。单元测试通常…...

编程日记 2023/10/22 22:34:53

golang 反射机制

在 go 语言中，实现反射能力的是 reflect包，能够让程序操作不同类型的对象。其中，在反射包中有两个非常重要的 类型和 函数，两个函数分别是： reflect.TypeOfreflect.ValueOf 两个类型是 reflect.Type 和 reflect.Value…...

编程日记 2023/10/22 22:33:52

【Javascript】创建对象的几种方式

通过字面量创建对象 通过构造函数创建对象 Object()-------------构造函数 通过构造函数来实例化对象 给person注入属性 Factory工厂 this指向的是对象的本身使⽤new 实例化⼀个对象，就像⼯⼚⼀样...

编程日记 2023/10/22 22:32:51

深度学习_3_实战_房价预测

梯度 实战 代码： # %matplotlib inline import random import torch import matplotlib.pyplot as plt # from d21 import torch as d21def synthetic_data(w, b, num_examples):"""生成 Y XW b 噪声。"""X torch.normal(0,…...

编程日记 2023/10/22 22:31:50

HCIA -- 动态路由协议之RIP

一、静态协议的优缺点： 缺点： 1、中大型网络配置量过大 2、不能基于拓扑的变化而实时的变化 优点： 1、不会额外暂用物理资源 2、安全问题 3、计算路径问题 简单、小型网络建议使用静态路由；中大型较复杂网络，建议使用…...

编程日记 2023/10/22 22:29:48

JS常用时间操作moment.js参考文档

Moment.js是一个轻量级的JavaScript时间库，它方便了日常开发中对时间的操作，提高了开发效率。日常开发中，通常会对时间进行下面这几个操作：比如获取时间，设置时间，格式化时间，比较时间等等。下面…...

编程日记 2023/10/22 22:27:46

基于 FFmpeg 的跨平台视频播放器简明教程（九）：Seek 策略

系列文章目录 基于 FFmpeg 的跨平台视频播放器简明教程（一）：FFMPEG Conan 环境集成基于 FFmpeg 的跨平台视频播放器简明教程（二）：基础知识和解封装（demux）基于 FFmpeg 的跨平台视频…...

编程日记 2023/10/22 22:25:45

设计模式_备忘录模式

备忘录模式 介绍 设计模式定义案例问题堆积在哪里解决办法备忘录模式行为型模式， 保存了数据某一个时间点的状态 在需要的时候进行回档单机游戏的角色 数据保存并且回档保存和回档加一个状态管理类 类图 代码 MomentData using UnityEngine;public class MomentD…...

编程日记 2023/10/22 22:24:44

双势阱模型

双势阱模型 原子钟 传统的原子钟利用氨分子 由于隧道效应，上顶点的氮原子可以贯穿三个氢原子形成的势垒，到达下顶点对体系注入微波能量后，氮原子在上下定点之间振荡，体系的能量在两个稳定态之间交替变换，其振荡频率决…...

编程日记 2023/10/22 22:21:40

文献阅读：The Reversal Curse: LLMs trained on “A is B” fail to learn “B is A”

文献阅读：The Reversal Curse: LLMs trained on “A is B” fail to learn “B is A” 1. 文章简介2. 实验 & 结果考察 1. finetune实验2. 真实知识问答 3. 结论 & 思考 文献链接：https://arxiv.org/abs/2309.12288 1. 文章简介 这篇文章是前…...

编程日记 2023/10/22 22:20:39

真实感受：是智能家居在选择合适的技术！

科技从来都是为了让我们的生活更加的简单、舒适，而智能家居的智能，体现在如何更更更方便的使用我需要控制的家居。 例如：下班躺在床上想休息，房间和大厅的灯还开着，这时你会选择什么产品躺着解决问题？ 红外…...

编程日记 2023/10/22 22:19:38

前端 TS 快速入门之二：接口

1. 接口有什么用 通过 interface 定义接口。 检测对象的属性，不会去检查属性的顺序，只要相应的属性存在并且类型也是对的就可以。 interface IPerson {name: string;age: number; } function say(person: IPerson): void {console.log(my name is ${pers…...

编程日记 2023/10/22 22:18:36

论文生成器（论文、文献综述、开题报告……），Java、Python、C++

“让论文生成器为您省时省力，轻松写出高质量的论文！” 2022年，腾讯全球数字生态大会腾讯云智能专场发布。 链接：http://xiezuo.saiertewl.cn/tb/xrWQed?dCodeh1xDrXmuhZbKPKgI&couponCodexiaoweilunwen...

编程日记 2023/10/22 22:17:35

【Java基础面试三十六】、遇到过异常吗，如何处理？

文章底部有个人公众号：热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享？ 踩过的坑没必要让别人在再踩，自己复盘也能加深记忆。利己利人、所谓双赢。 面试官：遇到过异常吗&#xff0…...

编程日记 2023/10/22 22:16:33

DASCTF-CBCTF-2023 Crypto部分复现

文章目录 EzRSACB backpack 这次比赛没打，记错时间了，看了一下，如果去做的话大概也只能做出那两道简单的题，还是太菜啦 EzRSA 题目描述： from Crypto.Util.number import * import random from gmpy2 import * from …...

编程日记 2023/10/22 22:15:30

为什么要做字节对齐 alignment？

下面这段 C 代码的输出是什么&#xff1f;定义的 Type 占用的字节数&#xff08;下面简称为字节数&#xff09;是多少呢&#xff1f; #include <iostream>struct Type {char a;int b; };int main(void) {std::cout << sizeof(Type) << \n; }经过编译运行&am…...

编程日记 2023/10/22 22:14:29

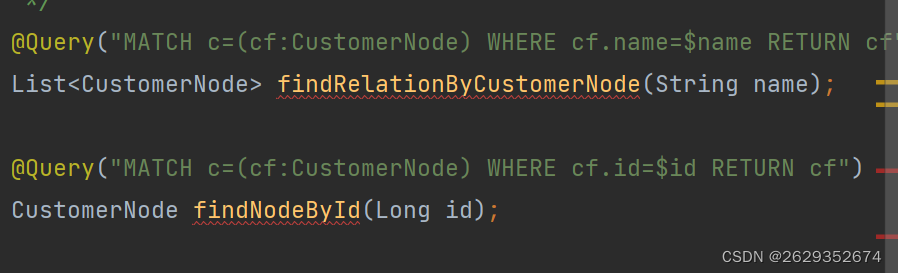
（零基础学习）Neo4j+Spring boot 自行定义属性

前置知识 1.Neo4j :属性 节点和关系都可以设置自己的属性。 属性是由Key-Value键值对组成&#xff0c;键名是字符串。属性值是要么是原始值&#xff0c;要么是原始值类型的一个数组。比如String&#xff0c;int和iint[]都是合法的。 注意 null不是一个合法的属性值。 Nulls能…...

编程日记 2023/10/22 22:13:29

【JavaEE】Java的文件IO

文件IO操作 Linux 下的文件操作讲解Java中的文件操作 -- 对文件的增删改查Java中对文件内容的操作 -- 读写操作使用案例 Linux 下的文件操作讲解 在我的Linux栏目下有, 如有需要, 点击下面进行跳转: 内存级文件系统语言级别的文教操作磁盘文件 Java中的文件操作 – 对文件的…...

编程日记 2023/10/22 22:12:28

华为云AI开发平台ModelArts

华为云ModelArts&#xff1a;重塑AI开发流程的“智能引擎”与“创新加速器”&#xff01; 在人工智能浪潮席卷全球的2025年&#xff0c;企业拥抱AI的意愿空前高涨&#xff0c;但技术门槛高、流程复杂、资源投入巨大的现实&#xff0c;却让许多创新构想止步于实验室。数据科学家…...

编程新知 2026/2/8 4:37:19

XCTF-web-easyupload

试了试php&#xff0c;php7&#xff0c;pht&#xff0c;phtml等&#xff0c;都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接&#xff0c;得到flag...

编程新知 2026/2/8 3:54:15

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾&#xff1a; 在上一篇中&#xff0c;我们成功地为应用集成了数据库&#xff0c;并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了&#xff01;但是&#xff0c;如果你仔细审视那些 API&#xff0c;会发现它们还很“粗糙”&#xff1a;有…...

编程新知 2026/1/22 20:46:43

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

Python如何给视频添加音频和字幕

在Python中&#xff0c;给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加&#xff0c;包括必要的代码示例和详细解释。 环境准备 在开始之前&#xff0c;需要安装以下Python库&#xff1a;…...

编程新知 2025/9/3 4:12:17

SpringCloudGateway 自定义局部过滤器

场景&#xff1a; 将所有请求转化为同一路径请求&#xff08;方便穿网配置&#xff09;在请求头内标识原来路径&#xff0c;然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

编程新知 2026/2/1 4:53:36

jmeter聚合报告中参数详解

sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample&#xff08;样本数&#xff09; 表示测试中发送的请求数量&#xff0c;即测试执行了多少次请求。 单位&#xff0c;以个或者次数表示。 示例&#xff1a;…...

编程新知 2025/12/18 6:00:45

LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别（二）

在上一篇文章中，我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调，以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后，如何调用这个模型进行人脸情感识别的具体代码实现，包括详细的步骤和注释。 模型调用步骤 环境准备：确保安装了必要的Python库。…...

编程新知 2025/11/4 0:47:29

QT开发技术【ffmpeg + QAudioOutput】音乐播放器

一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下&#xff0c;音视频内容犹如璀璨繁星&#xff0c;点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频&#xff0c;到在线课堂中知识渊博的专家授课&#xff0c;再到影视平台上扣人心弦的高清大片&#xff0c;音…...

编程新知 2026/2/8 23:54:57

图解JavaScript原型：原型链及其分析 | JavaScript图解

​​ 忽略该图的细节&#xff08;如内存地址值没有用二进制&#xff09; 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么&#xff1a;保存在堆中一块区域&#xff0c;同时在栈中有一块区域保存其在堆中的地址&#xff08;也就是我们通常说的该变量指向谁&…...

编程新知 2026/2/5 3:03:00