【蓝桥每日一题]-动态规划 (保姆级教程 篇10)#方格取数
高能预警:讲了这么久动态规划了,该上点有难度的题吧
目录
题目:方格取数
思路(解法一):
解法二:
题目:方格取数



思路(解法一):
如果只有两个方向的话,动态规划就很简单了,因为很容易就能根据已确定点推出未确定点(因为每个未知点都可以由上方和左方的已知点推出)。但是三个方向就不行了,因为全是未确定点。
既然这样的话我们就设置 up[i][j],down[i][j] 分别代表从下面向上面走到(i,j),从上面向下面走到(i,j)能取到的最大值;f[i][j]表示(i,j)处最终可取到的最大值
转移方程就好写了:
up[i][j]=max(up[i+1][j],f[i][j-1])+a[i][j];//可以从两个方向过来
down[i][j]=max(down[i-1][j],f[i][j-1])+a[i][j];//同理
f[i][j]=max(up[i][j],down[i][j]);//取最大值呀
因为数据比较大,所以我们要压缩成一维(因为我们在状态转移的时候只用到了j-1列的数据,故可以降一维,只需我们把列放外面即可。不明白的可以看动归最开始讲的那里)
故得到://这个f[i]是上一列的,初始化时候别搞错了
up[i]=max(up[i+1],f[i])+a[i][j];down[i]=max(down[i-1],f[i])+a[i][j];
f[i]=max(up[i],down[i])
#include <bits/stdc++.h> //(单向)方格取数
using namespace std;//动态规划
int n,m,a[1001][1001];
long long up[1005],down[1005],f[1005];
int main(){cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>a[i][j];f[1]=a[1][1];for(int i=2;i<=n;i++) f[i]=f[i-1]+a[i][1];//初始化第一列的每行for(int j=2;j<m;j++){//每次用上一列的数据memset(down,0,sizeof(down));//我们只需要关注行的数据即可,故需要循环一次初始化一次memset(up,0,sizeof(up));down[1]=f[1]+a[1][j];up[n]=f[n]+a[n][j];for(int i=2;i<=n;i++) down[i]=max(f[i],down[i-1])+a[i][j];for(int i=n-1;i>=1;i--) up[i]=max(f[i],up[i+1])+a[i][j];for(int i=1;i<=n;i++) f[i]=max(down[i],up[i]);//因为每列要么只向上,要么只向下,故取优即可}f[1]+=a[1][m];//因为最后一列只能向下走,故单独处理for(int i=2;i<=n;i++) f[i]=max(f[i],f[i-1])+a[i][m];//向下处理printf("%lld",f[n]);return 0;
}
解法二:
都说dp不好理解,那就再来个dfs吧
我们设置 f(i, j, 0)表示从下面走到该各格子(i, j)对应最优解,f(i, j, 1)表示从上面走到该格子对应最优解。
那么递推公式:
f(i,j,0)=max(f(i+1,j,0),f(i,j-1,0),f(i,j-1,1))
f(i,j,1)=max(f(i-1,j,1),f(i,j-1,0),f(i,j-1,1))
这样的话一共只需要跑n*m*2即可获得所有结果,所以和dp一样快
#include <stdio.h>
typedef long long LL; //记忆化搜索(和dp一样快)
const LL min_ll=-1e18;
int n,m;
LL w[1005][1005],f[1005][1005][2];
inline LL mx(LL p,LL q,LL r) {return p>q ? (p>r ? p:r) : (q>r ? q:r);}//三叶判断最快
inline LL dfs(int x, int y, int from) {if (x<1 || x>n || y<1 || y>m) return min_ll;if (f[x][y][from] != min_ll) return f[x][y][from];//记忆化if (from == 0) f[x][y][from] = mx(dfs(x+1,y,0), dfs(x,y-1,0), dfs(x,y-1,1))+w[x][y];else f[x][y][from] = mx(dfs(x-1,y,1), dfs(x,y-1,0), dfs(x,y-1,1))+w[x][y];return f[x][y][from];
}
int main(void) {scanf("%d %d", &n, &m);for (int i=1; i<=n; ++i)for (int j=1; j<=m; ++j) {scanf("%lld", &w[i][j]);f[i][j][0]=f[i][j][1]=min_ll;}f[1][1][0]=f[1][1][1]=w[1][1];//标记终点的值,到这个状态就直接返回,也就是dfs的结束条件printf("%lld\n",dfs(n,m,1));return 0;
}好,那么好,如果你能看到这里,那么你真的很厉害了已经,下面讲双向类型的。
相关文章:

【蓝桥每日一题]-动态规划 (保姆级教程 篇10)#方格取数
高能预警:讲了这么久动态规划了,该上点有难度的题吧 目录 题目:方格取数 思路(解法一): 解法二: 题目:方格取数 思路(解法一): 如果只有两个方向…...
Git GUI工具:SourceTree代码管理
Git GUI工具:SourceTree SourceTreeSourceTree的安装SourceTree的使用 总结 SourceTree 当我们对Git的提交、分支已经非常熟悉,可以熟练使用命令操作Git后,再使用GUI工具,就可以更高效。 Git有很多图形界面工具,这里…...

4 OpenCV实现多目三维重建(多张图片增量式生成稀疏点云)【附源码】
本文是基于 OpenCV4.80 进行的,关于环境的配置可能之后会单独说,先提一嘴 vcpkg 真好用 1 大致流程 从多张图片逐步生成稀疏点云,这个过程通常包括以下步骤: 初始重建: 初始两张图片的选择十分重要,这是整…...

【Java基础面试三十九】、 finally是无条件执行的吗?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: finally是无条件执行的…...

【讲座笔记】基于 Apache Calcite 的多引擎指标管理最佳实践|CommunityOverCode Asia 2023 | 字节开源
引言 三个问题 (问题解法) 1套SQL 2种语法 统一SQL的实践案例 虚拟列的实践案例 SQL Define Function 指标管理的实现 在这里插入图片描述...
蓝桥杯 (猜生日、棋盘放麦子、MP3储存 C++)
思路: 1、用循环。 2、满足条件,能整除2012、3、12且month等于6、day<30 #include<iostream> using namespace std; int main() {for (int i 19000101; i < 20120312; i){int month i / 100 % 100;int day i % 100;if (i % 2012 0 &…...
)
求 k 整除最大元素和(dp)
Description 给你一个整数数组,请你在其中选取若干个元素, 使得其和值能被 k 整除,输出和值最大的那个和值。 最后的数字可能很大,所以结果需要对 19260817 取模。 Input 第一行是两个正整数 n,k:表示数…...
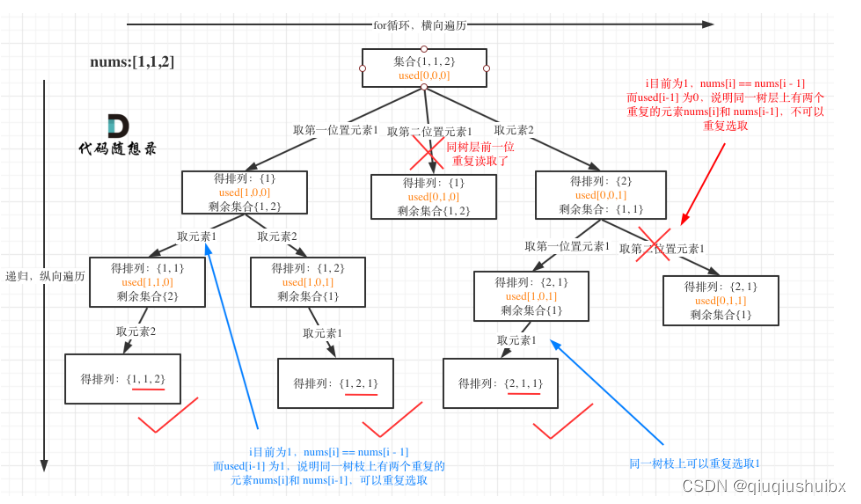
代码随想录Day24 LeetCode T491 递增子序列 LeetCode T46 全排列 LrrtCode T47 全排列II
LeetCode T491 递增子序列 题目链接:491. 递增子序列 - 力扣(LeetCode) 题目思路: 首先这里的测试用例很容易误导我们,这道题不能使用上次子集的思路对数组先排序,使用一个used数组来解决问题. 我们用[4,7,6,7]举例这道题的递增序列不存在[4,6,7,7]这个…...
【六:(mock数据)spring boot+mybatis+yml】
目录 1.1、代码编写Demo类User类启动类 APplication 1.2、配置类查询语句的配置 mysql.ymlspringboot的配置 application.yml日志的配置 logback.xml数据库的配置 mybatis-config.xml 1.3、测试:1.3.1、测试获取用户数1.3.2、添加用户1.3.3、数据的更新1.3.4、数据的…...

51单片机KeyWard
eg1: 单片机键盘的分类 键盘分为编码键盘和非编码键盘,键盘上闭合键的识别由专用的硬件编码器实现,并产生键编码号或键值得称为编码键盘,如计算机键盘,而靠软件来识别的称为非编码键盘,在单片机组成的各种…...

【简记】getprop, setprop 命令使用
getprop, setprop 命令使用 1、终端设置、读取系统属性 // 例 adb shell setprop "test" "1" adb shell getprop "test"2、安卓读取系统配置 部分属性需要通过反射 android.os.SystemProperties 的方法获取,参见 android 获取手机…...

Ubuntu22.04安装nvidia-docker
安装docker 参考这篇文章:Ubuntu22.04安装docker - 掘金 安装nvidia-docker 参考这篇文章:Ubuntu 22.04 LTS : NVIDIA Container Toolkit : Install : Server World 流程: curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | …...
)
简单的代码优化(后端)
上一篇谈了谈简单的前端的优化,这次就以下几点谈谈后端的优化。 书写时常见的。 循环里面不要走IO流。 走IO,是要对硬盘进读写操作的。就结论而言,硬盘的读写速度是低于内存的,比如说硬盘上读一次数据,需要1秒&#…...

3.Node-事件循环的用法
题记 node.js事件循环的使用方法 Node.js 是单进程单线程应用程序,但是因为 V8 引擎提供的异步执行回调接口,通过这些接口可以处理大量的并发,所以性能非常高。 Node.js 几乎每一个 API 都是支持回调函数的。 Node.js 基本上所有的事件机制都…...
2525.根据规则将箱子分类/并查集/动态规划
2525. 根据规则将箱子分类 - 力扣(LeetCode) 给你四个整数 length ,width ,height 和 mass ,分别表示一个箱子的三个维度和质量,请你返回一个表示箱子 类别 的字符串。 如果满足以下条件,那么…...
2023年10月小程序云开发cms内容管理无法使用,无法同步内容模型到云开发数据库的解决方案
一,问题描述 最近越来越多的同学找石头哥,说cms用不了,其实是小程序官方最近又搞大动作了,偷偷的升级的云开发cms(内容管理)以下都称cms,不升级不要紧,这一升级,就导致我…...

无论有没有按钮,iPhone都可以进行截屏操作!如何在iPhone上截屏
通过简单的按键组合,可以很容易地将iPhone屏幕的图片捕获到图像文件中,并保存到照片库中。以下是操作方法。 什么是屏幕截图 屏幕截图是指通常包含你在设备屏幕上看到的内容的精确副本的图像。在设备内拍摄的数字屏幕截图通常使用相机拍摄物理屏幕的照…...

笔记本平台信号讲解
1、power button:这个信号会引起SMI#或者SCI来表示系统请求进入到睡眠状态。如果系统已经处于睡眠状态,这将导致唤醒事件信号。 如果PWRBTN#键超过4秒,这将导致一个无条件的过渡(电源按钮替代)到S5状态。即使系统是在S1-S4的状态,覆盖也会发生。 这个信号有一个内部上拉…...
什么是Sectigo证书?
Sectigo证书,早前被称为Comodo证书,是一种SSL(安全套接层)证书,用于保护互联网上的数据传输的安全性和隐私性。这些证书由全球领先的SSL证书颁发机构Sectigo颁发,被广泛用于网站、应用程序和服务器上。本文…...

虹科 | 测试方案 | 汽车示波器 通讯网络(LIN/CAN/FlexRay)测试方案
通讯网络(LIN/CAN/FlexRay)测试 虹科CAN总线示波器把你的PC电脑变成一台功能强大的汽车测试工具,用于检测车辆网络各类通讯信号,如CAN Bus、CAN FD、LIN、FlexRay,还可以检测车上所有传感器和执行器的信号 串行译码 …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
