简单单调栈的运用,悬线法---最大子矩阵,整除分块(规律+分块边界)
简单单调栈的运用
牛客一站到底 最优屏障
题意:有n座山,高度位ai,山上的士兵能相互监督当且仅当max(ai+1...aj-1)<min(ai,aj)
M国的防守能力大小为相互监视的哨兵对数,H国家可以放一块巨大屏障在某山前,以便最大消弱M方式能力
计算最优的屏障放置位置和最大的防守力减少量
n≤50000
思路:屏障的放置将大区间分为左右两个独立区间,知道大区间的的值
在枚举屏障放置点,关键在与预处理左右两个独立区间
用栈处理左右区间,分为从后往前看,从前往后看两种
处理,添加一个数进来,能产生对数的是前面比之小的单调递减区间
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define endl '\n'
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define fr(i,z,n) for(int i = z;i <= n; i++)
#define ufr(i,n,z) for(int i = n;i >= z; i--)
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ;
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
int v1[maxn]; //记录从后往前看
int v2[maxn]; //从前往后看
stack<int>s;signed main()
{int t;scanf("%d", &t);for (int Case = 1; Case <= t; Case++) {memset(v1, 0, sizeof(v1));memset(v2, 0, sizeof(v2));while (!s.empty()) {s.pop();}int n;scanf("%d", &n);fr(i, 1, n) {scanf("%d", &a[i]);}for (int i = 1; i <= n; i++) { //从后往前看v1[i] = v1[i - 1];int t = 0;while (!s.empty() && s.top() < a[i]) {s.pop();t++;}if (!s.empty()) v1[i] += t + 1;else v1[i] += t;s.push(a[i]);}while (!s.empty()) {s.pop();}for (int i = n; i >= 1; i--) { //从前往后看v2[i] = v2[i + 1];int t = 0;while (!s.empty() && s.top() < a[i]) {s.pop();t++;}if (!s.empty()) v2[i] += t + 1;else v2[i] += t;s.push(a[i]);}int ans = 0, id = 0;fr(i, 1, n) {int x = v1[n] - (v1[i] + v2[i + 1]);if (x > ans) {ans = x;id = i;}}id += 1;//Case #1: 2 2cout << "Case #" << Case << ": " << id << ' ' << ans << '\n';}
}
悬线法---最大子矩阵
HISTOGRA - Largest Rectangle in a Histogram
在一条水平线上有 n 个宽为1 的矩形,求包含于这些矩形的最大子矩形面积、
时间复杂度O(n)
#include <algorithm>
#include <cstdio>
using std::max;
const int N = 100010;
int n, a[N];
int l[N], r[N]; //l[i]表示a[i]向左能扩展到的位置,r[i]表示向右能扩展到的位置
long long ans;int main() {while (scanf("%d", &n) != EOF && n) {ans = 0;for (int i = 1; i <= n; i++) scanf("%d", &a[i]), l[i] = r[i] = i;for (int i = 1; i <= n; i++)while (l[i] > 1 && a[i] <= a[l[i] - 1]) l[i] = l[l[i] - 1];for (int i = n; i >= 1; i--)while (r[i] < n && a[i] <= a[r[i] + 1]) r[i] = r[r[i] + 1];for (int i = 1; i <= n; i++)ans = max(ans, (long long)(r[i] - l[i] + 1) * a[i]);printf("%lld\n", ans);}return 0;
}
P4147 玉蟾宫
给定n*m的矩阵,每一格为F或R,找到最大的全为F的矩形土地,输出面积*3
n<=m<=1000
思路:同HISTOGRA - Largest Rectangle in a Histogram,将每一行的位置向上扩展作为悬线长度
时间复杂度O(n*m)
#include <algorithm>
#include <cstdio>
#include<iostream>
using namespace std;
int m, n, a[1010], l[1010], r[1010], ans;
int main() {cin >> n >> m;int ans = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {l[j] = r[j] = j;}char s;for (int j = 1; j <= m; j++) {cin >> s;if (s == 'F') {a[j]++;}else {a[j] = 0;}} for (int j = 1; j <= m; j++) {while (l[j] > 1 && a[j] <= a[l[j] - 1])l[j] = l[l[j] - 1];}for (int j = m; j >=1; j--) {while (r[j] < m && a[j] <= a[r[j] + 1]) r[j] = r[r[j] + 1];}for (int j = 1; j <= m; j++) {ans = max(ans, a[j] * (r[j] - l[j] + 1));}} cout << 3*ans << '\n';
}
洛谷
感觉不错 Feel Good
给出正整数n 和一个长度为n 的数列a,要求找出一个子区间[l, r],
使这个子区间的数字和乘上子区间中的最小值最大。输出这个最大值与区间的两个端点
在答案相等的情况下最小化区间长度,最小化长度的情况下最小化左端点序号。
思路:寻找每一个结点的左右扩展,利用前缀和求出答案
#include <cstdio>
#include <cstring>
const int N = 100010;
int n, a[N], l[N], r[N];
long long sum[N];
long long ans;
int ansl, ansr;
bool fir = 1;int main() {while (scanf("%d", &n) != EOF) {memset(a, -1, sizeof(a));if (!fir)printf("\n");elsefir = 0;ans = 0;ansl = ansr = 1;for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);sum[i] = sum[i - 1] + a[i];l[i] = r[i] = i;}for (int i = 1; i <= n; i++)while (a[l[i] - 1] >= a[i]) l[i] = l[l[i] - 1];for (int i = n; i >= 1; i--)while (a[r[i] + 1] >= a[i]) r[i] = r[r[i] + 1];for (int i = 1; i <= n; i++) {long long x = a[i] * (sum[r[i]] - sum[l[i] - 1]);if (ans < x || (ans == x && ansr - ansl > r[i] - l[i]))ans = x, ansl = l[i], ansr = r[i];}printf("%lld\n%d %d\n", ans, ansl, ansr);}return 0;
}整除分块(规律+分块边界)
1.f(n)=n/i的和 (1<=i<=n)
以l为左边界,k=n/l, 右边界r为k的最大下标i,找到最大的i满足i<=n/k
带入k,r=n/(n/l)
#include<iostream>
using namespace std;
int main()
{ int ans = 0;int n;cin >> n;for (int l = 1, r; l <= n; l = r + 1) {r = n / (n / l);cout << l << ' ' << r << '\n';ans += (n / l) * (r - l + 1);}cout << ans << '\n';return 0;
}
P1403 [AHOI2005] 约数研究
f(n)表示n的约数的个数
求f(i)的和 (1<=i<=n)
思路:约数的性质满足每个正约数i在1~n中出现的个为n/i
直接套用整除分块板子
#include<iostream>
using namespace std;
int main()
{int ans = 0;int n;cin >> n;for (int l = 1, r; l <= n; l = r + 1) {r = n / (n / l);//cout << l << ' ' << r << '\n';ans += (n / l) * (r - l + 1);}cout << ans << '\n';return 0;
}
P2424 约数和
f(x)表示x的所有约数和,求f(x)+f(x+1)...+f(y)
思路:约数的性质满足每个正约数i在1~n中出现的个为n/i,于是约数对总和的贡献为i*n/i
在区间[l,r]满足n/i为常数,等差数列求出
ans=cal(y)-cla(x-1)
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
int a[1000];
int cal(int n) {int res = 0;for (int l = 1, r; l <= n; l = r + 1) {r = n / (n / l);//res += (n / l) * (r - l + 1) / 2;res += (n / l) * (l + r) * (r - l + 1) / 2;}return res;
}
signed main()
{int x, y;cin >> x >> y;cout << cal(y) - cal(x - 1) << '\n';return 0;
}
P2261 [CQOI2007] 余数求和
给定n,k,计算k%i的和,求(1<=i<=n)
n,k<=1e9
思路:对于a%b -> a-b*(a/b)
k%i ->k-i*(k/i)
ans=k-i*(k/i)的和 (1<=i<=n)
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
signed main()
{int n, k;cin >> n >> k;int ans = n*k;for (int l = 1, r; l <= n; l = r + 1) {if (k / l != 0) //防止rer = min(k / (k / l), n);elser = n;ans -= (k / l) * (l + r) * (r - l + 1) / 2;}cout << ans << '\n';return 0;
}相关文章:
)
简单单调栈的运用,悬线法---最大子矩阵,整除分块(规律+分块边界)
简单单调栈的运用 牛客一站到底 最优屏障 题意:有n座山,高度位ai,山上的士兵能相互监督当且仅当max(ai1...aj-1)<min(ai,aj) M国的防守能力大小为相互监视的哨兵对数,H国家可以放一块巨大屏障在某山前,以便最大消弱M方式能力 计算最优的屏…...
【java】A卷+B卷)
华为OD 数组求和(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

Go语言入门心法(十):Go语言操作MYSQL(CRUD)|事务处理
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 Go语言入门心法(六): HTTP面向客户端|服务端编程 Go语言入门心法(七): 并发与通道 Go语言入门心法(八): mysql驱动安装报错o…...

【鸿蒙软件开发】进度条Progress
文章目录 前言一、进度条Progress1.1 创建进度条1.2 进度条样式进度条样式ProgressType.Linear(线性样式)ProgressType.Ring(环形无刻度样式)ProgressType.ScaleRing(环形有刻度样式)ProgressType.Eclipse&…...
-- idea(2022版)将commit(未push)的 本地仓库 的 多条commit记录 进行撤销)
Java后端开发(九)-- idea(2022版)将commit(未push)的 本地仓库 的 多条commit记录 进行撤销
目录 1.多次 修改Test01类后,提交到本地仓库 。 2.多次重复 1 的步骤,多次commit成功后,在Git =》Log中会显示,commit记录...

【蓝桥每日一题]-动态规划 (保姆级教程 篇10)#方格取数
高能预警:讲了这么久动态规划了,该上点有难度的题吧 目录 题目:方格取数 思路(解法一): 解法二: 题目:方格取数 思路(解法一): 如果只有两个方向…...
Git GUI工具:SourceTree代码管理
Git GUI工具:SourceTree SourceTreeSourceTree的安装SourceTree的使用 总结 SourceTree 当我们对Git的提交、分支已经非常熟悉,可以熟练使用命令操作Git后,再使用GUI工具,就可以更高效。 Git有很多图形界面工具,这里…...

4 OpenCV实现多目三维重建(多张图片增量式生成稀疏点云)【附源码】
本文是基于 OpenCV4.80 进行的,关于环境的配置可能之后会单独说,先提一嘴 vcpkg 真好用 1 大致流程 从多张图片逐步生成稀疏点云,这个过程通常包括以下步骤: 初始重建: 初始两张图片的选择十分重要,这是整…...

【Java基础面试三十九】、 finally是无条件执行的吗?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: finally是无条件执行的…...

【讲座笔记】基于 Apache Calcite 的多引擎指标管理最佳实践|CommunityOverCode Asia 2023 | 字节开源
引言 三个问题 (问题解法) 1套SQL 2种语法 统一SQL的实践案例 虚拟列的实践案例 SQL Define Function 指标管理的实现 在这里插入图片描述...
蓝桥杯 (猜生日、棋盘放麦子、MP3储存 C++)
思路: 1、用循环。 2、满足条件,能整除2012、3、12且month等于6、day<30 #include<iostream> using namespace std; int main() {for (int i 19000101; i < 20120312; i){int month i / 100 % 100;int day i % 100;if (i % 2012 0 &…...
)
求 k 整除最大元素和(dp)
Description 给你一个整数数组,请你在其中选取若干个元素, 使得其和值能被 k 整除,输出和值最大的那个和值。 最后的数字可能很大,所以结果需要对 19260817 取模。 Input 第一行是两个正整数 n,k:表示数…...
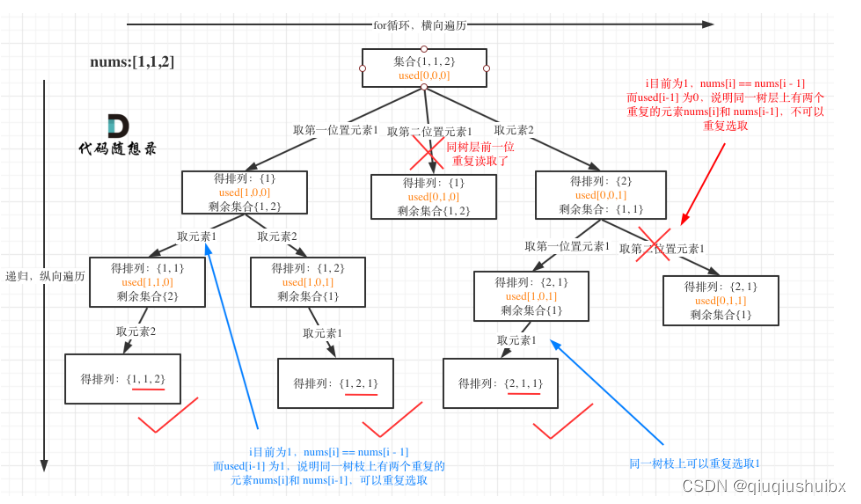
代码随想录Day24 LeetCode T491 递增子序列 LeetCode T46 全排列 LrrtCode T47 全排列II
LeetCode T491 递增子序列 题目链接:491. 递增子序列 - 力扣(LeetCode) 题目思路: 首先这里的测试用例很容易误导我们,这道题不能使用上次子集的思路对数组先排序,使用一个used数组来解决问题. 我们用[4,7,6,7]举例这道题的递增序列不存在[4,6,7,7]这个…...
【六:(mock数据)spring boot+mybatis+yml】
目录 1.1、代码编写Demo类User类启动类 APplication 1.2、配置类查询语句的配置 mysql.ymlspringboot的配置 application.yml日志的配置 logback.xml数据库的配置 mybatis-config.xml 1.3、测试:1.3.1、测试获取用户数1.3.2、添加用户1.3.3、数据的更新1.3.4、数据的…...

51单片机KeyWard
eg1: 单片机键盘的分类 键盘分为编码键盘和非编码键盘,键盘上闭合键的识别由专用的硬件编码器实现,并产生键编码号或键值得称为编码键盘,如计算机键盘,而靠软件来识别的称为非编码键盘,在单片机组成的各种…...

【简记】getprop, setprop 命令使用
getprop, setprop 命令使用 1、终端设置、读取系统属性 // 例 adb shell setprop "test" "1" adb shell getprop "test"2、安卓读取系统配置 部分属性需要通过反射 android.os.SystemProperties 的方法获取,参见 android 获取手机…...

Ubuntu22.04安装nvidia-docker
安装docker 参考这篇文章:Ubuntu22.04安装docker - 掘金 安装nvidia-docker 参考这篇文章:Ubuntu 22.04 LTS : NVIDIA Container Toolkit : Install : Server World 流程: curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | …...
)
简单的代码优化(后端)
上一篇谈了谈简单的前端的优化,这次就以下几点谈谈后端的优化。 书写时常见的。 循环里面不要走IO流。 走IO,是要对硬盘进读写操作的。就结论而言,硬盘的读写速度是低于内存的,比如说硬盘上读一次数据,需要1秒&#…...

3.Node-事件循环的用法
题记 node.js事件循环的使用方法 Node.js 是单进程单线程应用程序,但是因为 V8 引擎提供的异步执行回调接口,通过这些接口可以处理大量的并发,所以性能非常高。 Node.js 几乎每一个 API 都是支持回调函数的。 Node.js 基本上所有的事件机制都…...
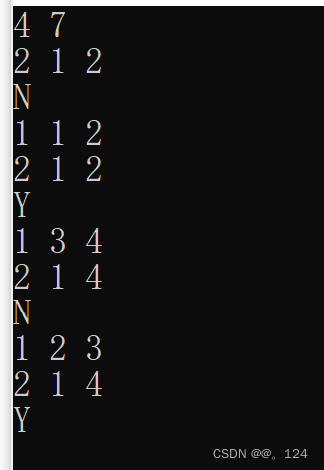
2525.根据规则将箱子分类/并查集/动态规划
2525. 根据规则将箱子分类 - 力扣(LeetCode) 给你四个整数 length ,width ,height 和 mass ,分别表示一个箱子的三个维度和质量,请你返回一个表示箱子 类别 的字符串。 如果满足以下条件,那么…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
