Leetcode 第 364 场周赛题解
Leetcode 第 364 场周赛题解
- Leetcode 第 364 场周赛题解
- 题目1:2864. 最大二进制奇数
- 思路
- 代码
- 复杂度分析
- 题目2:美丽塔 I
- 思路
- 代码
- 复杂度分析
- 题目3:美丽塔 II
- 思路
- 代码
- 复杂度分析
- 题目4:统计树中的合法路径数目
- 思路
- 代码
- 复杂度分析
Leetcode 第 364 场周赛题解
题目1:2864. 最大二进制奇数
思路
贪心。
要得到最大二进制奇数,则高位尽可能放 1,为了是奇数,最后一位必须是 1。
设原字符串的长度为 n,统计原字符串中 ‘1’ 的个数,记为 count_one。
新字符串 = count_one - 1 个 ‘1’ + n - count_one 个 ‘0’ + ‘1’。
代码
/** @lc app=leetcode.cn id=2864 lang=cpp** [2864] 最大二进制奇数*/// @lc code=start
class Solution
{
public:string maximumOddBinaryNumber(string s){int n = s.size(), count_one = 0;for (char &c : s)if (c == '1')count_one++;string ans;for (int i = 0; i < count_one - 1; i++)ans += '1';for (int i = 0; i < n - count_one; i++)ans += '0';ans += '1';return ans;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 是字符串的长度。
空间复杂度:O(1)。
题目2:美丽塔 I
思路
枚举峰值的位置,向左、向右求高度和,更新高度和的最大值。
代码
/** @lc app=leetcode.cn id=2865 lang=cpp** [2865] 美丽塔 I*/// @lc code=start
class Solution
{
public:long long maximumSumOfHeights(vector<int> &maxHeights){int n = maxHeights.size();long long max_sum = 0;// 枚举峰值的位置for (int i = 0; i < n; i++){long long cur_sum = maxHeights[i];// 向左求和int left_height = maxHeights[i];for (int j = i - 1; j >= 0; j--){left_height = min(left_height, maxHeights[j]);cur_sum += left_height;}// 向右求和int right_height = maxHeights[i];for (int j = i + 1; j < n; j++){right_height = min(right_height, maxHeights[j]);cur_sum += right_height;}// 更新答案max_sum = max(max_sum, cur_sum);}return max_sum;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n2),其中 n 是数组 maxHeights 的长度。
空间复杂度:O(1)。
题目3:美丽塔 II
思路
思考优化:
以示例 [6,5,3,9,2,7] 为例,我们观察以 3 和 9 作为山顶的两个方案:
- 以 3 作为山顶:3 3 |3 3| 2 2
- 以 9 作为山顶:3 3 |3 9| 2 2
可以发现:以 3 作为山顶的左侧与以 9 为山顶的右侧在两个方案之间是可以复用的,至此发现解决方法:我们可以分别预处理出以每个节点作为山顶的前缀和后缀的和:
- prev[i] 表示以 maxHeights[i] 作为山顶时左侧段的前缀和;
- suffix[i] 表示以 maxHeights[i] 作为山顶时右侧段的后缀和。
那么,最佳方案就是 prev[i]+suffix[i]−maxHeight[i] 的最大值。 现在,最后的问题是如何以均摊 O(1) 的时间复杂度计算出每个元素前后缀的和?
继续以示例 [6,5,3,9,2,7] 为例:
- 以 6 为山顶,前缀为 [6]
- 以 5 为山顶,需要保证左侧元素不大于 5,因此找到 666 并修改为 555,前缀为 [5,5]
- 以 3 为山顶,需要保证左侧元素不大于 3,因此找到两个 555 并修改为 333,前缀为 [3,3,3]
- 以 9 为山顶,需要保证左侧元素不大于 9,不需要修改,前缀为 [3,3,3,9]
- 以 2 为山顶,需要保证左侧元素不大于 2,修改后为 [2,2,2,2,2]
- 以 7 为山顶,需要保证左侧元素不大于 7,不需要修改,前缀为 [2,2,2,2,2,7]
观察以上步骤,问题的关键在于修改操作:由于数组是递增的,因此修改的步骤就是在「寻找小于等于当前元素 x 的上一个元素」,再将中间的元素削减为 x。「寻找上一个更小元素」,这是单调栈的典型场景。
代码
/** @lc app=leetcode.cn id=2866 lang=cpp** [2866] 美丽塔 II*/// @lc code=start
class Solution
{
public:long long maximumSumOfHeights(vector<int> &maxHeights){int n = maxHeights.size();vector<long long> suffix(n + 1, 0);vector<long long> prev(n + 1, 0);stack<int> s;// 单调栈求前缀for (int i = 0; i < n; i++){// 弹出栈顶while (!s.empty() && maxHeights[s.top()] > maxHeights[i])s.pop();int j = s.empty() ? -1 : s.top();prev[i + 1] = prev[j + 1] + (long long)(i - j) * maxHeights[i];s.push(i);}// 清空栈while (!s.empty())s.pop();// 单调栈求后缀for (int i = n - 1; i >= 0; i--){// 弹出栈顶while (!s.empty() && maxHeights[s.top()] > maxHeights[i])s.pop();int j = s.empty() ? n : s.top();suffix[i] = suffix[j] + (long long)(j - i) * maxHeights[i];s.push(i);}// 合并long long max_sum = 0;for (int i = 0; i < n; i++)max_sum = max(max_sum, prev[i + 1] + suffix[i] - maxHeights[i]);return max_sum;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 是数组 maxHeights 的长度。在一侧的计算中,每个元素最多如何和出栈 1 次。
空间复杂度:O(n),其中 n 是数组 maxHeights 的长度。
题目4:统计树中的合法路径数目
超出能力范围。
思路
经典的树型 DP 模型。维护以下值:
- fu 表示以节点 u 为起点,以 u 的子树中某个节点为终点的路径中,所有点编号都是合数的路径有几条。
- gu 表示以节点 u 为起点,以 u 的子树中某个节点为终点的路径中,有一个点的编号为质数的路径有几条。
answer += f[u] * g[v] + f[v] * g[u]。
题解:
https://leetcode.cn/problems/count-valid-paths-in-a-tree/solutions/2456568/shu-dp-by-tsreaper-of6v/
【图解】O(n) 线性做法(Python/Java/C++/Go)
代码
/** @lc app=leetcode.cn id=2867 lang=cpp** [2867] 统计树中的合法路径数目*/// @lc code=start// 树型 DPclass Solution
{
private:#define MAXN (int)1e5bool inited = false;bool flag[MAXN + 10];// 筛法预处理 1e5 以内的质数void init(){if (inited)return;inited = true;memset(flag, 0, sizeof(flag));flag[0] = flag[1] = true;for (int i = 2; i * i <= MAXN; i++)if (!flag[i])for (int j = i << 1; j <= MAXN; j += i)flag[j] = true;}public:long long countPaths(int n, vector<vector<int>> &edges){init();vector<int> e[n + 1];for (auto &edge : edges){e[edge[0]].push_back(edge[1]);e[edge[1]].push_back(edge[0]);}long long ans = 0;int f[n + 1], g[n + 1];// 树 dpfunction<void(int, int)> dfs = [&](int sn, int fa){if (flag[sn])f[sn] = 1, g[sn] = 0;elsef[sn] = 0, g[sn] = 1;for (int fn : e[sn])if (fn != fa){dfs(fn, sn);// 路径上深度最低的节点为 sn,这样的合法路径有几条ans += f[sn] * g[fn] + g[sn] * f[fn];// 更新以 sn 为起点,且走到子树里的路径数量if (flag[sn]){f[sn] += f[fn];g[sn] += g[fn];}else{g[sn] += f[fn];}}};dfs(1, 0);return ans;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 是数组 edges 的长度。
空间复杂度:O(n),其中 n 是数组 edges 的长度。
相关文章:

Leetcode 第 364 场周赛题解
Leetcode 第 364 场周赛题解 Leetcode 第 364 场周赛题解题目1:2864. 最大二进制奇数思路代码复杂度分析 题目2:美丽塔 I思路代码复杂度分析 题目3:美丽塔 II思路代码复杂度分析 题目4:统计树中的合法路径数目思路代码复杂度分析 …...
)
简单单调栈的运用,悬线法---最大子矩阵,整除分块(规律+分块边界)
简单单调栈的运用 牛客一站到底 最优屏障 题意:有n座山,高度位ai,山上的士兵能相互监督当且仅当max(ai1...aj-1)<min(ai,aj) M国的防守能力大小为相互监视的哨兵对数,H国家可以放一块巨大屏障在某山前,以便最大消弱M方式能力 计算最优的屏…...
【java】A卷+B卷)
华为OD 数组求和(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

Go语言入门心法(十):Go语言操作MYSQL(CRUD)|事务处理
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 Go语言入门心法(六): HTTP面向客户端|服务端编程 Go语言入门心法(七): 并发与通道 Go语言入门心法(八): mysql驱动安装报错o…...

【鸿蒙软件开发】进度条Progress
文章目录 前言一、进度条Progress1.1 创建进度条1.2 进度条样式进度条样式ProgressType.Linear(线性样式)ProgressType.Ring(环形无刻度样式)ProgressType.ScaleRing(环形有刻度样式)ProgressType.Eclipse&…...
-- idea(2022版)将commit(未push)的 本地仓库 的 多条commit记录 进行撤销)
Java后端开发(九)-- idea(2022版)将commit(未push)的 本地仓库 的 多条commit记录 进行撤销
目录 1.多次 修改Test01类后,提交到本地仓库 。 2.多次重复 1 的步骤,多次commit成功后,在Git =》Log中会显示,commit记录...

【蓝桥每日一题]-动态规划 (保姆级教程 篇10)#方格取数
高能预警:讲了这么久动态规划了,该上点有难度的题吧 目录 题目:方格取数 思路(解法一): 解法二: 题目:方格取数 思路(解法一): 如果只有两个方向…...
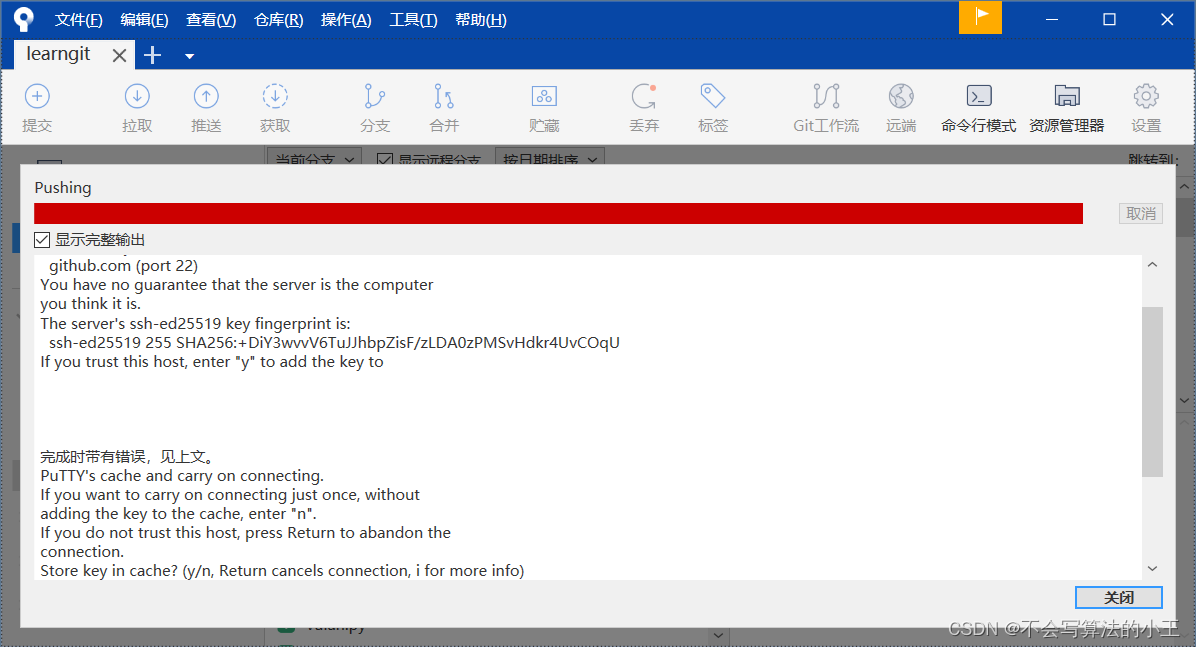
Git GUI工具:SourceTree代码管理
Git GUI工具:SourceTree SourceTreeSourceTree的安装SourceTree的使用 总结 SourceTree 当我们对Git的提交、分支已经非常熟悉,可以熟练使用命令操作Git后,再使用GUI工具,就可以更高效。 Git有很多图形界面工具,这里…...

4 OpenCV实现多目三维重建(多张图片增量式生成稀疏点云)【附源码】
本文是基于 OpenCV4.80 进行的,关于环境的配置可能之后会单独说,先提一嘴 vcpkg 真好用 1 大致流程 从多张图片逐步生成稀疏点云,这个过程通常包括以下步骤: 初始重建: 初始两张图片的选择十分重要,这是整…...

【Java基础面试三十九】、 finally是无条件执行的吗?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: finally是无条件执行的…...

【讲座笔记】基于 Apache Calcite 的多引擎指标管理最佳实践|CommunityOverCode Asia 2023 | 字节开源
引言 三个问题 (问题解法) 1套SQL 2种语法 统一SQL的实践案例 虚拟列的实践案例 SQL Define Function 指标管理的实现 在这里插入图片描述...
蓝桥杯 (猜生日、棋盘放麦子、MP3储存 C++)
思路: 1、用循环。 2、满足条件,能整除2012、3、12且month等于6、day<30 #include<iostream> using namespace std; int main() {for (int i 19000101; i < 20120312; i){int month i / 100 % 100;int day i % 100;if (i % 2012 0 &…...
)
求 k 整除最大元素和(dp)
Description 给你一个整数数组,请你在其中选取若干个元素, 使得其和值能被 k 整除,输出和值最大的那个和值。 最后的数字可能很大,所以结果需要对 19260817 取模。 Input 第一行是两个正整数 n,k:表示数…...
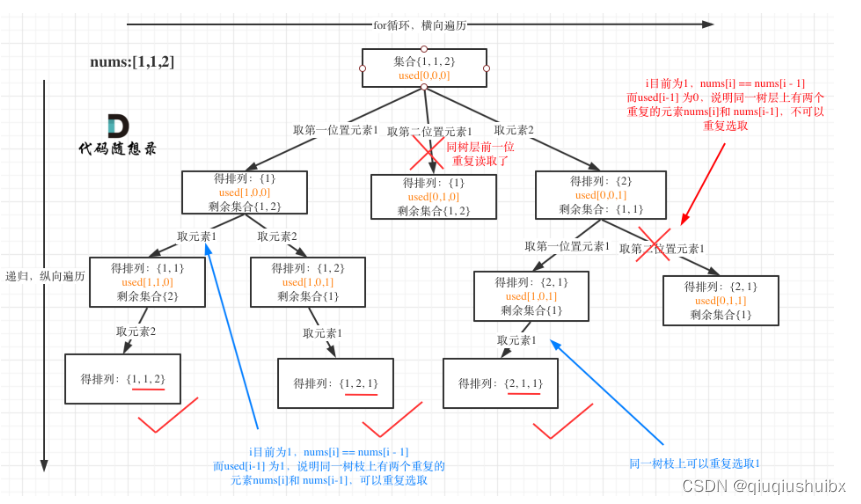
代码随想录Day24 LeetCode T491 递增子序列 LeetCode T46 全排列 LrrtCode T47 全排列II
LeetCode T491 递增子序列 题目链接:491. 递增子序列 - 力扣(LeetCode) 题目思路: 首先这里的测试用例很容易误导我们,这道题不能使用上次子集的思路对数组先排序,使用一个used数组来解决问题. 我们用[4,7,6,7]举例这道题的递增序列不存在[4,6,7,7]这个…...
【六:(mock数据)spring boot+mybatis+yml】
目录 1.1、代码编写Demo类User类启动类 APplication 1.2、配置类查询语句的配置 mysql.ymlspringboot的配置 application.yml日志的配置 logback.xml数据库的配置 mybatis-config.xml 1.3、测试:1.3.1、测试获取用户数1.3.2、添加用户1.3.3、数据的更新1.3.4、数据的…...

51单片机KeyWard
eg1: 单片机键盘的分类 键盘分为编码键盘和非编码键盘,键盘上闭合键的识别由专用的硬件编码器实现,并产生键编码号或键值得称为编码键盘,如计算机键盘,而靠软件来识别的称为非编码键盘,在单片机组成的各种…...

【简记】getprop, setprop 命令使用
getprop, setprop 命令使用 1、终端设置、读取系统属性 // 例 adb shell setprop "test" "1" adb shell getprop "test"2、安卓读取系统配置 部分属性需要通过反射 android.os.SystemProperties 的方法获取,参见 android 获取手机…...

Ubuntu22.04安装nvidia-docker
安装docker 参考这篇文章:Ubuntu22.04安装docker - 掘金 安装nvidia-docker 参考这篇文章:Ubuntu 22.04 LTS : NVIDIA Container Toolkit : Install : Server World 流程: curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | …...
)
简单的代码优化(后端)
上一篇谈了谈简单的前端的优化,这次就以下几点谈谈后端的优化。 书写时常见的。 循环里面不要走IO流。 走IO,是要对硬盘进读写操作的。就结论而言,硬盘的读写速度是低于内存的,比如说硬盘上读一次数据,需要1秒&#…...

3.Node-事件循环的用法
题记 node.js事件循环的使用方法 Node.js 是单进程单线程应用程序,但是因为 V8 引擎提供的异步执行回调接口,通过这些接口可以处理大量的并发,所以性能非常高。 Node.js 几乎每一个 API 都是支持回调函数的。 Node.js 基本上所有的事件机制都…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
