Leetcode 2911. Minimum Changes to Make K Semi-palindromes
- Leetcode 2911. Minimum Changes to Make K Semi-palindromes
- 1. 解题思路
- 2. 代码实现
- 题目链接:2911. Minimum Changes to Make K Semi-palindromes
1. 解题思路
这一题属实也是把我坑惨了……
坦率地说,这道题本身并没有啥难度,但是坑爹的是题目表述简直有毒,有两个细节题目里面压根没提,一个是我从中文版本的题目当中发现的,另一个则是我根据失败的样例当中反推出来的,这简直有毒……
这道题本身思路上还是挺直接的,就是一个动态规划的题目,考虑每一种切分的方式,然后考察其中最小的变化次数即可。
然后对于每一个切分得到的子串,我们要求其变化所需的最小变化次数,我们只需要找到其所有对长度 l l l整除的 d d d,然后切分semi子串,再考察其中每一种分法下所需的变化次数之和,最后取最小值即可。
因此,我们就将上述题目拆分完成了,后续只要对其实现一下即可,测试发现是可以在有效时间内完成所有测试样例的。
但是,这里但是就来了,题目中遗漏了两个非常非常重要的说明,把我给坑惨了!!!
首先,这里semi-palindrome的定义事实上要求将其使用d进行切分后,每一个子串都得是回文,其次,题中也没有具体说,但是实际测试发现,这里对子串的切分要求每一个子串长度至少为2。
这简直就是简直了!!!
到底谁出的题目啊,只能说,出来挨打!!!
2. 代码实现
给出python代码实现如下:
class Solution:def minimumChanges(self, s: str, k: int) -> int:n = len(s)@lru_cache(None)def count(sub):cnt = 0n = len(sub)for i in range(n//2):if sub[i] != sub[n-1-i]:cnt += 1return cnt@lru_cache(None)def count_change(s):if s == s[::-1]:return 0n = len(s)ans = count(s)for d in range(len(s)//2, 0, -1):if n % d != 0:continuek = n // dcnt = 0for i in range(d):sub = "".join([s[i+j*d] for j in range(k)])cnt += count(sub)ans = min(ans, cnt)return ans@lru_cache(None)def dp(idx, k):if idx+2*k > n:return math.infelif k == 1:return count_change(s[idx:])return min(count_change(s[idx:j]) + dp(j, k-1) for j in range(idx+2, n))ans = dp(0, k)return ans
提交代码评测得到:耗时5650ms,占用内存71.8MB。
相关文章:

Leetcode 2911. Minimum Changes to Make K Semi-palindromes
Leetcode 2911. Minimum Changes to Make K Semi-palindromes 1. 解题思路2. 代码实现 题目链接:2911. Minimum Changes to Make K Semi-palindromes 1. 解题思路 这一题属实也是把我坑惨了…… 坦率地说,这道题本身并没有啥难度,但是坑爹…...
Node学习笔记之包管理工具
一、概念介绍 1.1 包是什么 『包』英文单词是package ,代表了一组特定功能的源码集合 1.2 包管理工具 管理『包』的应用软件,可以对「包」进行 下载安装 , 更新 , 删除 , 上传 等操作 借助包管理工具,可…...
分发糖果[困难]
优质博文:IT-BLOG-CN 一、题目 n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果: 【1】每个孩子至少分配到1个糖果。 【2】相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩…...

Java验证邮箱格式是否正确的正则表达式
Java验证邮箱格式是否正确的正则表达式 import java.util.regex.Pattern;public class EmailUtil {final static Pattern partern Pattern.compile("[a-zA-Z0-9][\\.]{0,1}[a-zA-Z0-9][a-zA-Z0-9]\\.[a-zA-Z]");/*** 验证输入的邮箱格式是否符合* param email* ret…...

快速排序原理JAVA和Scala实现-函数式编程的简洁演示
快速排序原理JAVA和Scala实现-函数式编程的简洁演示 目录 快速排序原理JAVA和Scala实现-函数式编程的简洁演示 C语言快速排序实现 Java 快速排序实现 Scala 快速排序实现 本文章向大家介绍快速排序原理JAVA和Scala实现-函数式编程的简洁演示,主要内容包括C语言…...
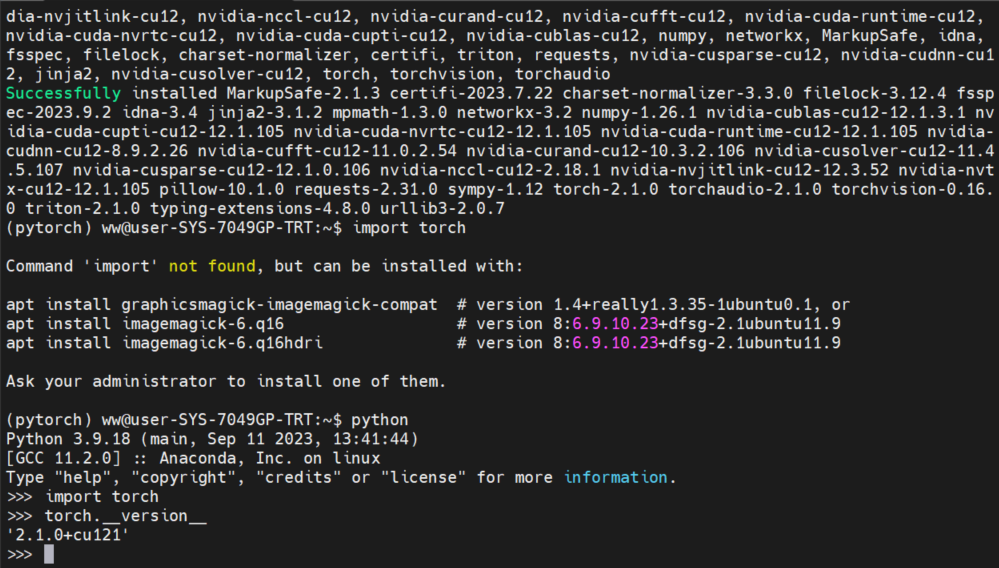
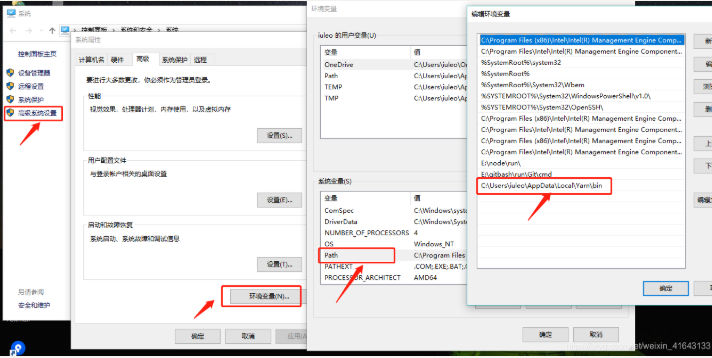
如何在linux服务器上安装Anaconda与pytorch
如何在linux服务器上安装Anaconda与pytorch 1,安装anaconda1.1 下载anaconda安装包1.2 安装anaconda1.3 设计环境变量1.4 安装完成验证 2 Anaconda安装pytorch2.1 创建虚拟环境2.2 查看现存环境2.3 激活环境2.4 选择合适的pytorch版本下载2.5 检测是否安装成功&…...
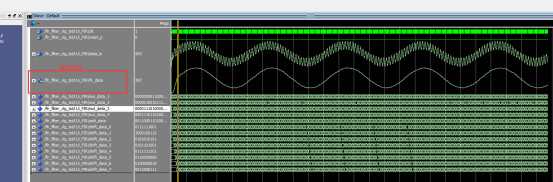
FPGA设计FIR滤波器低通滤波器,代码及视频
名称:FIR滤波器低通滤波器 软件:Quartus 语言:Verilog/VHDL 本资源含有verilog及VHDL两种语言设计的工程,每个工程均可实现以下FIR滤波器的功能。 代码功能: 设计一个8阶FIR滤波器(低通滤波器ÿ…...
【数据结构】排序--快速排序
目录 一 概念 二 快速排序的实现 1. hoare版本 (1)代码实现 (2)单趟排序图解 (3) 递归实现图解 (4)细节控制 (5)时间复杂度 (6)三数取中优化 2 挖坑法 (1)代码实现 (2)单趟图解 3 前后指针法 (1) 代码实现 (2) 单趟图解 4 优化子区间 5 非递归快速排序 …...
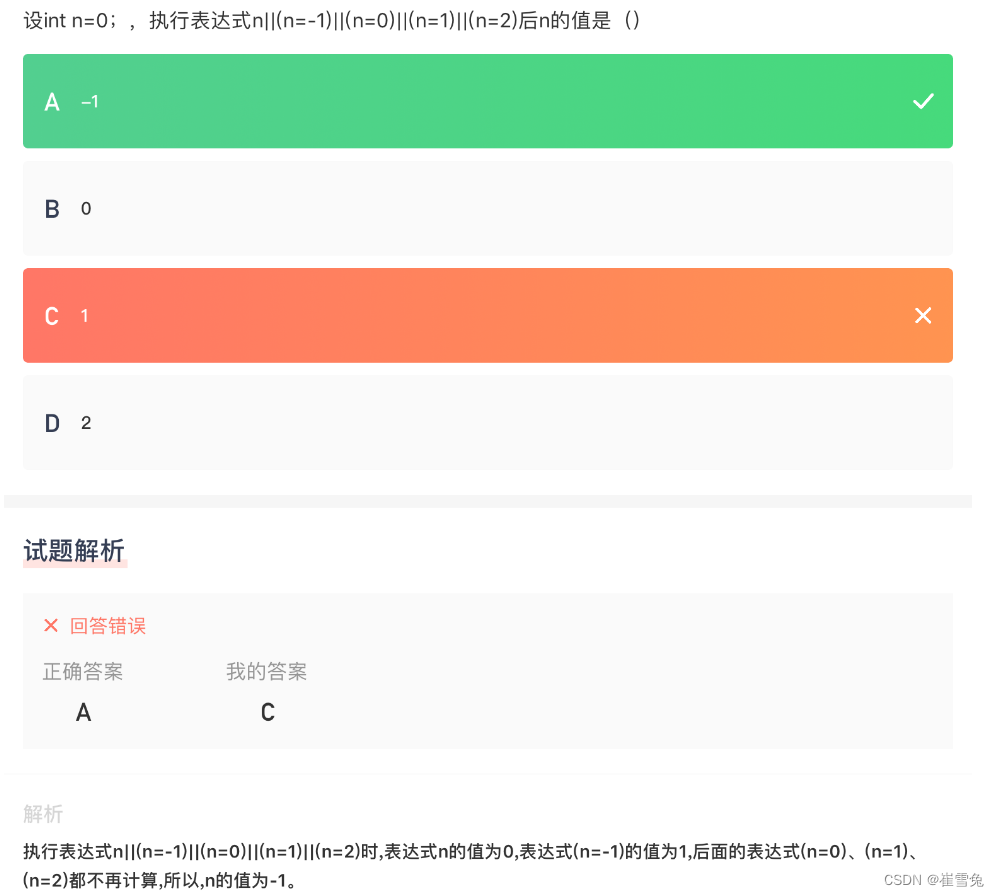
【试题040】多个逻辑或例题2
1.题目:设int n0;,执行表达式n ||(n-1) ||(n0)||(n1)||(n2)后n的值是 ? 2.代码解析: 逻辑或 || 运算符是一个短路运算符,它从左到右依次计算表达式,如果遇到一个为真(非零)的值&am…...

自然语言处理---Self Attention自注意力机制
Self-attention介绍 Self-attention是一种特殊的attention,是应用在transformer中最重要的结构之一。attention机制,它能够帮助找到子序列和全局的attention的关系,也就是找到权重值wi。Self-attention相对于attention的变化,其实…...
推荐收藏系列!2万字图解Hadoop
今天我用图解的方式讲解pandas的用法,内容较长建议收藏,梳理不易,点赞支持。 学习 Python 编程,给我的经验就是:技术要学会分享、交流,不建议闭门造车。一个人可能走的很快、但一堆人可以走的更远。如果你…...
:生成器)
Python高级篇(08):生成器
一、生成器定义和作用 定义:Python中,一边循环一边计算的机制,生成器对象也是迭代器对象,支持for循环、next()方法…等。作用:循环的过程中不断推算出后续的元素,这样就不必创建完整的list,从而…...
)
力扣100114. 元素和最小的山形三元组 II(中等)
题目描述: 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < knums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 nums 中 元素和最小 的山形三元组…...
--lcdseg - 段式lcd)
LuatOS-SOC接口文档(air780E)--lcdseg - 段式lcd
常量 常量 类型 解释 lcdseg.BIAS_STATIC number 没偏置电压(bias) lcdseg.BIAS_ONEHALF number 1/2偏置电压(bias) lcdseg.BIAS_ONETHIRD number 1/3偏置电压(bias) lcdseg.BIAS_ONEFOURTH number 1/4偏置电压(bias) lcdseg.DUTY_STATIC number 100%占空比(d…...

实现图像处理和分析的关键技术
在计算机视觉中,我们可以利用摄像头捕捉到的图像来进行各种分析和处理。以下是一些常见的计算机视觉任务: 对象检测:识别图像中的特定对象并标注其位置。人脸识别:识别和验证人脸身份。姿态估计:估计人体的姿态和动作…...

【C++学习笔记】内联函数
1. 概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数提升程序运行的效率。 如果在上述函数前增加inline关键字将其改成内联函数,在编译期间编译器会用函数…...
macOS Sonoma 14.1RC(23B73)发布
黑果魏叔10 月 18 日消息,苹果今日向 Mac 电脑用户推送了 macOS 14.1 RC更新(内部版本号:23B73),本次更新距离上次发布隔了 7 天。 macOS Sonoma 14.1RC(23B73)的更新内容主要包括以下方面&…...
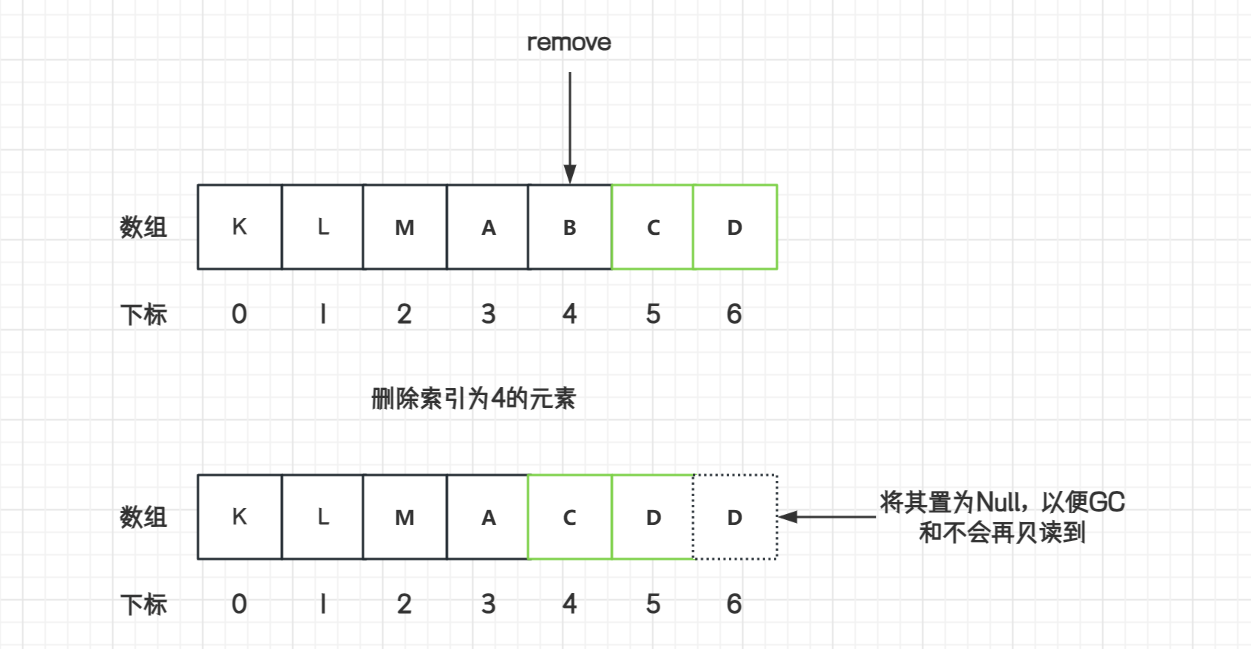
数据结构数组 Array 手写实现,扩容原理
数组数据结构 数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型数据的集合。 数组的特点: 数组是相同数据类型的元素集合(int 不能存放 double)数组中各元素的存储是有先…...
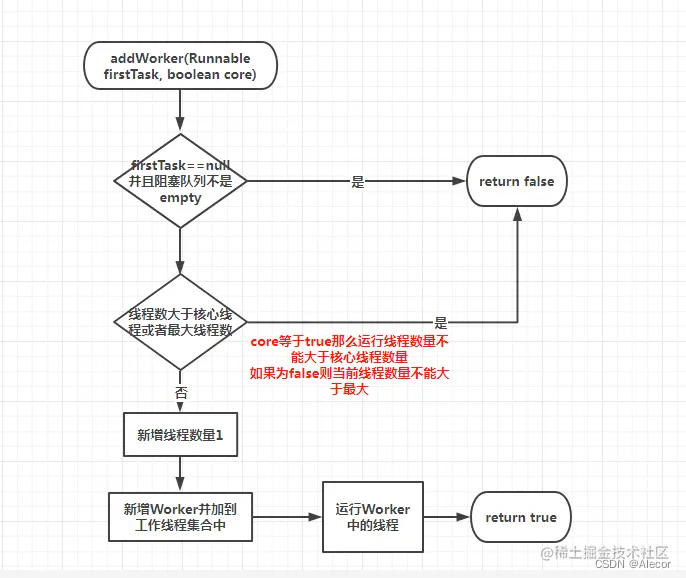
工作中几个问题的思考
对于需要并行多公司并行处理的任务,方案是什么? 多线程、并行流、并发库(ExecutorService、Futrue、Callable),分布式计算(1)按照公司ID分片 (2)按照业务类型分片 处理…...
Jmeter的性能测试
性能测试的概念 定义:软件的性能是软件的一种非功能特性,它关注的不是软件是否能够完成特定的功能,而是在完成该功能时展示出来的及时性。 由定义可知性能关注的是软件的非功能特性,所以一般来说性能测试介入的时机是在功能测试…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
