分发糖果[困难]
优质博文:IT-BLOG-CN
一、题目
n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果:
【1】每个孩子至少分配到1个糖果。
【2】相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发2、1、2颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发1、2、1颗糖果。第三个孩子只得到1颗糖果,这满足题面中的两个条件。
n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104
二、代码
【1】两次遍历: 我们可以将「相邻的孩子中,评分高的孩子必须获得更多的糖果」这句话拆分为两个规则,分别处理。
左规则: 当ratings[i−1] < ratings[i]时,i号学生的糖果数量将比i−1号孩子的糖果数量多。
右规则: 当ratings[i] > ratings[i+1]时,i号学生的糖果数量将比i+1号孩子的糖果数量多。
我们遍历该数组两次,处理出每一个学生分别满足左规则或右规则时,最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。
具体地,以左规则为例:我们从左到右遍历该数组,假设当前遍历到位置i,如果有ratings[i−1] < ratings[i]那么i号学生的糖果数量将比i−1号孩子的糖果数量多,我们令left[i]=left[i−1] + 1即可,否则我们令left[i] = 1。在实际代码中,我们先计算出左规则left数组,在计算右规则的时候只需要用单个变量记录当前位置的右规则,同时计算答案即可。
class Solution {public int candy(int[] ratings) {// 1、定义left[]数组,计算每个小朋友符合左侧规则时,能获取到的糖果// 2、定义两个变量,第一个计算前一个小朋友的糖果,第二个计算总的糖果数量,从右侧开始计算if (ratings.length == 0) {return 0;}// 创建数组int[] left = new int[ratings.length];left[0] = 1;for(int i = 1; i < ratings.length; i++) {if (ratings[i] > ratings[i - 1]) {left[i] = left[i - 1] + 1;} else {left[i] = 1;}}// 先初始化最后一个小朋友的糖果int next = 1, count = Math.max(1, left[ratings.length - 1]);for(int i = ratings.length - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {next += 1;} else {next = 1;}count += Math.max(next, left[i]);}return count;}
}
时间复杂度: O(2n)其中n是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
空间复杂度: O(n)其中n是孩子的数量。我们需要保存所有的左规则对应的糖果数量。
【2】常数空间遍历: 定义两个变量,第一个计算当前小朋友的糖果pre,第一个小朋友默认为1,第二个计算总的糖果数量count,如果时递增的,那么就比较简单,我们给pre+1,如果递减了,我们重置pre = 1即可。下面考虑两个特殊场景:
● 当pre=1时,开始递减时,我们需要再创建一个变量decr,来表示递减的次数,然后将其累积到count中,也就达到了将递减转化为递增的效果。
● 当递减的队列长度,超过了递减前小朋友的糖果时,我们需要对递减前的小朋友的糖果+n,例如下图: 从左侧遍历时,第三个小朋友应该是3个糖果,所以定义inc记录递减前小朋友的糖果,如果递减的糖果decr等于递减前的糖果inc,就需要对inc + 1;
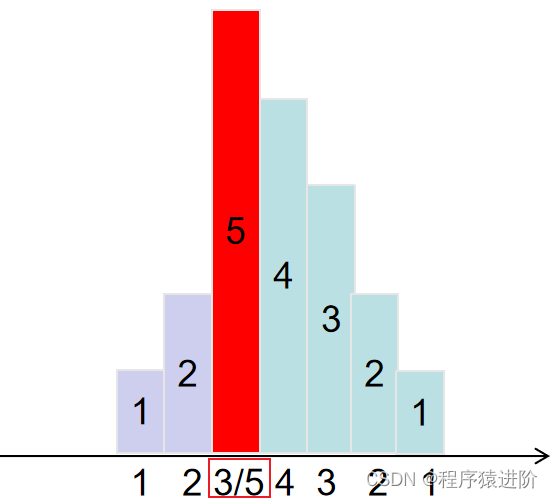
class Solution {public int candy(int[] ratings) {// 1、定义两个变量,第一个计算当前小朋友的糖果pre,第二个计算总的糖果数量count。// 2、左侧遍历时,如果时递减的情况,需要再创建一个变量,计算递减的次数 decr。// 3、特殊处理:递减的时候,如果我拥有的糖果和递减前小朋友的糖果个数相同时,需要++,举例:5321的时候,5有3个糖果,此时的3再递减中也会有5个糖果,所以就需要对5的糖果+1if (ratings.length == 0) {return 0;}// 先初始化最后一个小朋友的糖果int pre = 1, count = 1, decr = 0, inc = 1;for(int i = 1; i < ratings.length; i++) {if (ratings[i] >= ratings[i - 1]) {pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;;// 如果时递增的,当前递减序列结束decr = 0;count += pre;// pre表示当前小朋友用于的当过inc = pre;} else {// 如果开始了递减序列,我们就开始记录递减序列的长度decr++;// 递减的时候,如果我拥有的糖果和递减的小朋友的个数相同时,需要++,举例:5321的时候,5有3个糖果,此时的3再递减中也会有5个糖果,所以就需要对5+1if (inc == decr) {decr++;}// 重置糖果为1pre = 1;count += decr;}}return count;}
}
时间复杂度: O(n)其中n是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
空间复杂度: O(1)我们只需要常数的空间保存若干变量。
相关文章:

分发糖果[困难]
优质博文:IT-BLOG-CN 一、题目 n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果: 【1】每个孩子至少分配到1个糖果。 【2】相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩…...

Java验证邮箱格式是否正确的正则表达式
Java验证邮箱格式是否正确的正则表达式 import java.util.regex.Pattern;public class EmailUtil {final static Pattern partern Pattern.compile("[a-zA-Z0-9][\\.]{0,1}[a-zA-Z0-9][a-zA-Z0-9]\\.[a-zA-Z]");/*** 验证输入的邮箱格式是否符合* param email* ret…...

快速排序原理JAVA和Scala实现-函数式编程的简洁演示
快速排序原理JAVA和Scala实现-函数式编程的简洁演示 目录 快速排序原理JAVA和Scala实现-函数式编程的简洁演示 C语言快速排序实现 Java 快速排序实现 Scala 快速排序实现 本文章向大家介绍快速排序原理JAVA和Scala实现-函数式编程的简洁演示,主要内容包括C语言…...
如何在linux服务器上安装Anaconda与pytorch
如何在linux服务器上安装Anaconda与pytorch 1,安装anaconda1.1 下载anaconda安装包1.2 安装anaconda1.3 设计环境变量1.4 安装完成验证 2 Anaconda安装pytorch2.1 创建虚拟环境2.2 查看现存环境2.3 激活环境2.4 选择合适的pytorch版本下载2.5 检测是否安装成功&…...
FPGA设计FIR滤波器低通滤波器,代码及视频
名称:FIR滤波器低通滤波器 软件:Quartus 语言:Verilog/VHDL 本资源含有verilog及VHDL两种语言设计的工程,每个工程均可实现以下FIR滤波器的功能。 代码功能: 设计一个8阶FIR滤波器(低通滤波器ÿ…...
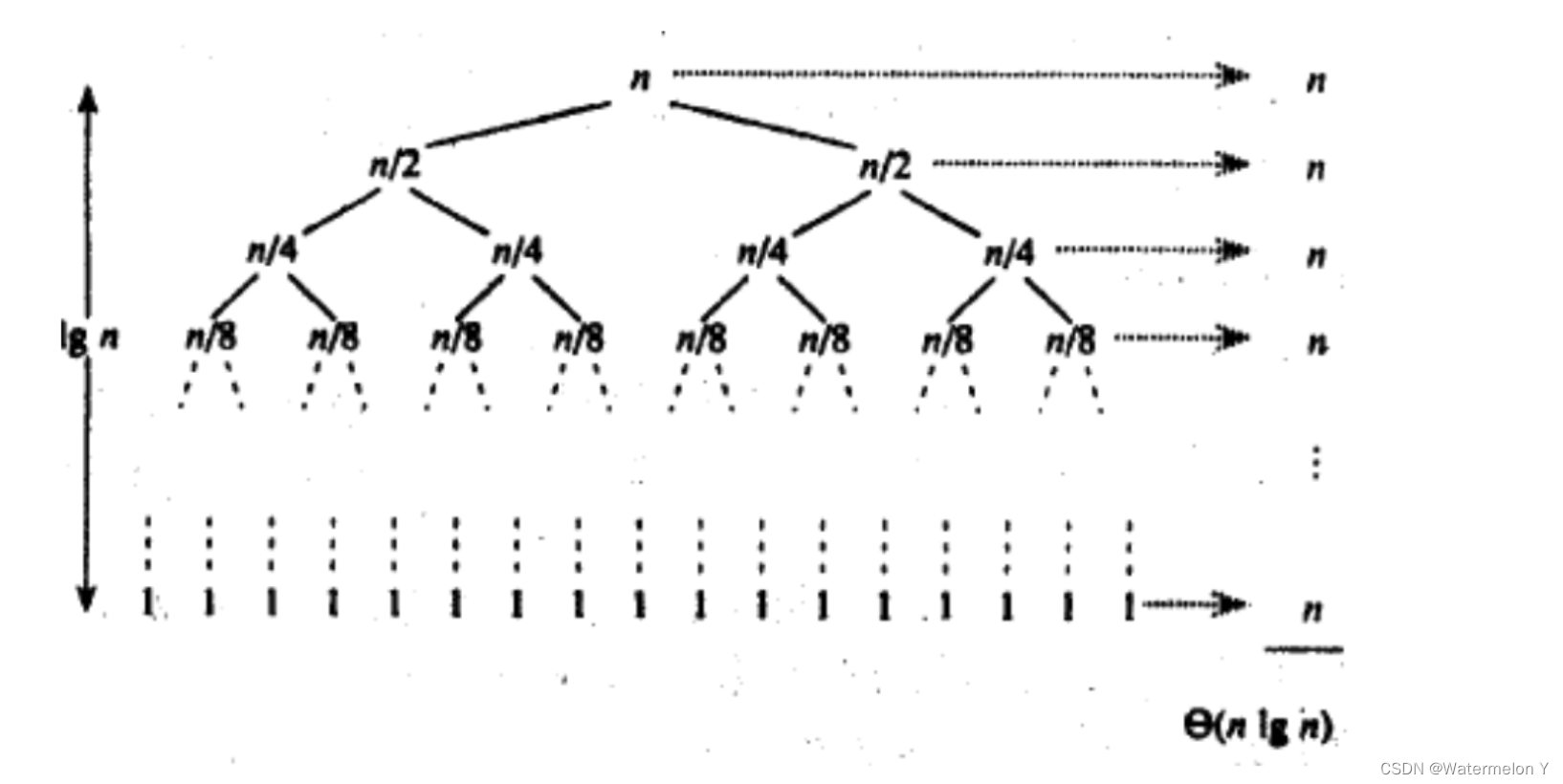
【数据结构】排序--快速排序
目录 一 概念 二 快速排序的实现 1. hoare版本 (1)代码实现 (2)单趟排序图解 (3) 递归实现图解 (4)细节控制 (5)时间复杂度 (6)三数取中优化 2 挖坑法 (1)代码实现 (2)单趟图解 3 前后指针法 (1) 代码实现 (2) 单趟图解 4 优化子区间 5 非递归快速排序 …...
【试题040】多个逻辑或例题2
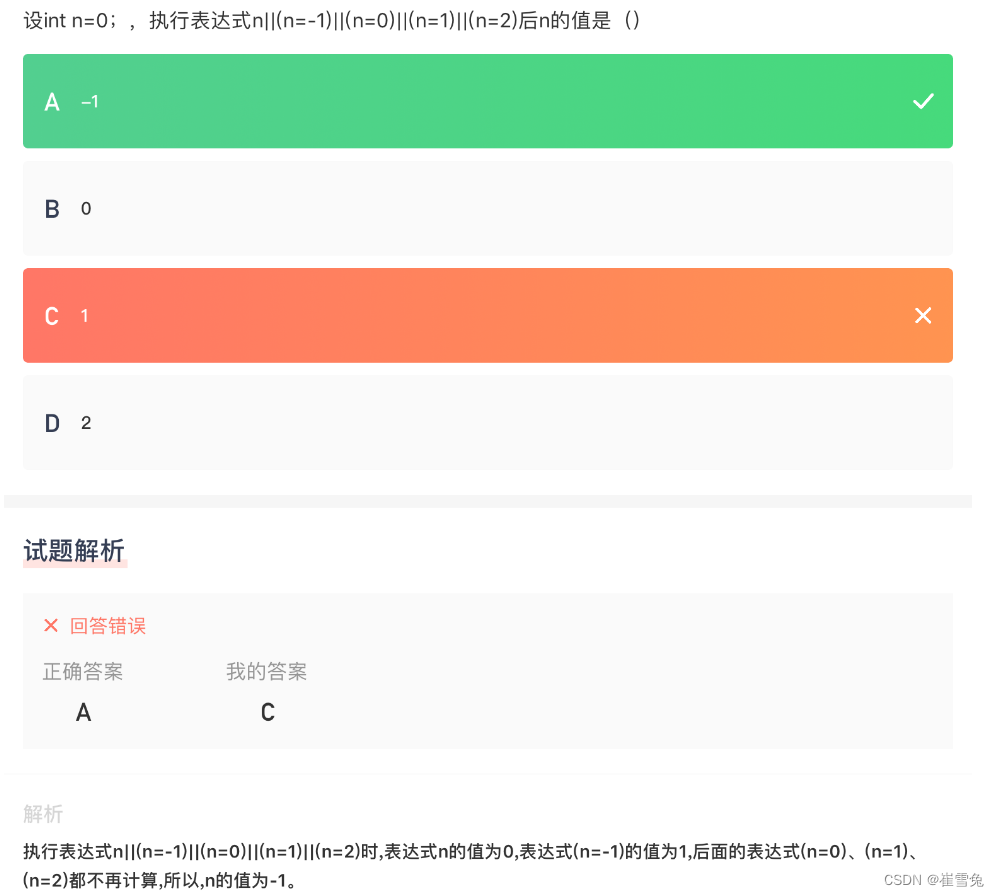
1.题目:设int n0;,执行表达式n ||(n-1) ||(n0)||(n1)||(n2)后n的值是 ? 2.代码解析: 逻辑或 || 运算符是一个短路运算符,它从左到右依次计算表达式,如果遇到一个为真(非零)的值&am…...

自然语言处理---Self Attention自注意力机制
Self-attention介绍 Self-attention是一种特殊的attention,是应用在transformer中最重要的结构之一。attention机制,它能够帮助找到子序列和全局的attention的关系,也就是找到权重值wi。Self-attention相对于attention的变化,其实…...
推荐收藏系列!2万字图解Hadoop
今天我用图解的方式讲解pandas的用法,内容较长建议收藏,梳理不易,点赞支持。 学习 Python 编程,给我的经验就是:技术要学会分享、交流,不建议闭门造车。一个人可能走的很快、但一堆人可以走的更远。如果你…...
:生成器)
Python高级篇(08):生成器
一、生成器定义和作用 定义:Python中,一边循环一边计算的机制,生成器对象也是迭代器对象,支持for循环、next()方法…等。作用:循环的过程中不断推算出后续的元素,这样就不必创建完整的list,从而…...
)
力扣100114. 元素和最小的山形三元组 II(中等)
题目描述: 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < knums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 nums 中 元素和最小 的山形三元组…...
--lcdseg - 段式lcd)
LuatOS-SOC接口文档(air780E)--lcdseg - 段式lcd
常量 常量 类型 解释 lcdseg.BIAS_STATIC number 没偏置电压(bias) lcdseg.BIAS_ONEHALF number 1/2偏置电压(bias) lcdseg.BIAS_ONETHIRD number 1/3偏置电压(bias) lcdseg.BIAS_ONEFOURTH number 1/4偏置电压(bias) lcdseg.DUTY_STATIC number 100%占空比(d…...

实现图像处理和分析的关键技术
在计算机视觉中,我们可以利用摄像头捕捉到的图像来进行各种分析和处理。以下是一些常见的计算机视觉任务: 对象检测:识别图像中的特定对象并标注其位置。人脸识别:识别和验证人脸身份。姿态估计:估计人体的姿态和动作…...

【C++学习笔记】内联函数
1. 概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数提升程序运行的效率。 如果在上述函数前增加inline关键字将其改成内联函数,在编译期间编译器会用函数…...
macOS Sonoma 14.1RC(23B73)发布
黑果魏叔10 月 18 日消息,苹果今日向 Mac 电脑用户推送了 macOS 14.1 RC更新(内部版本号:23B73),本次更新距离上次发布隔了 7 天。 macOS Sonoma 14.1RC(23B73)的更新内容主要包括以下方面&…...
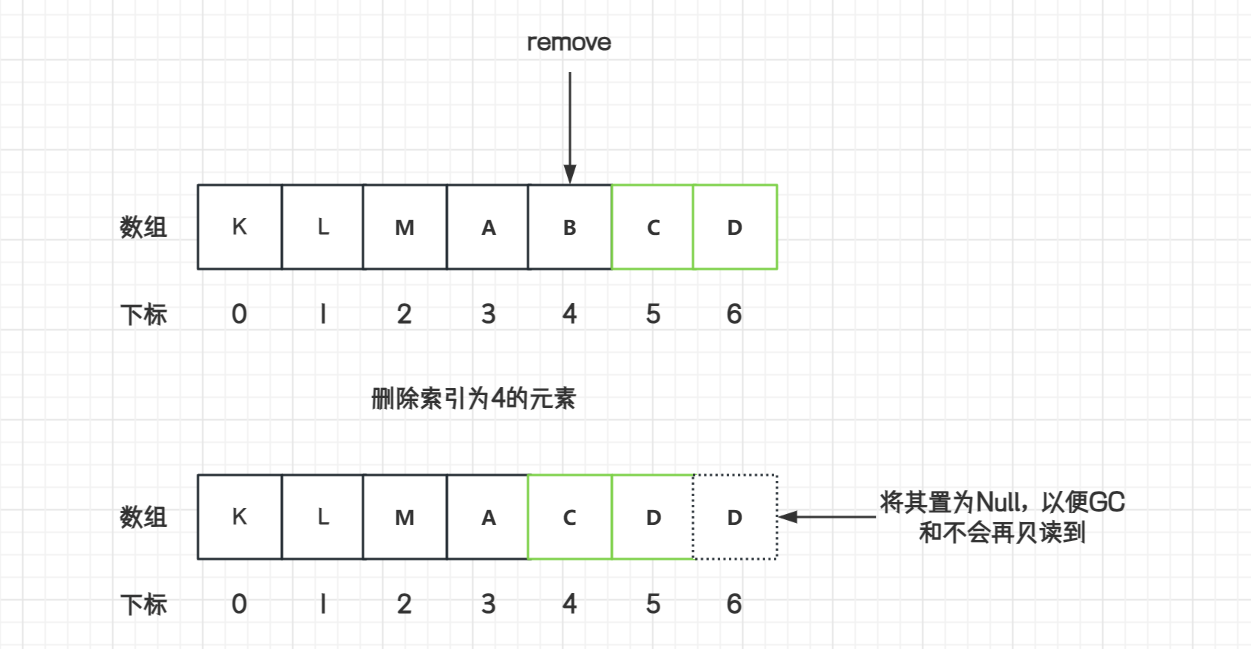
数据结构数组 Array 手写实现,扩容原理
数组数据结构 数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型数据的集合。 数组的特点: 数组是相同数据类型的元素集合(int 不能存放 double)数组中各元素的存储是有先…...
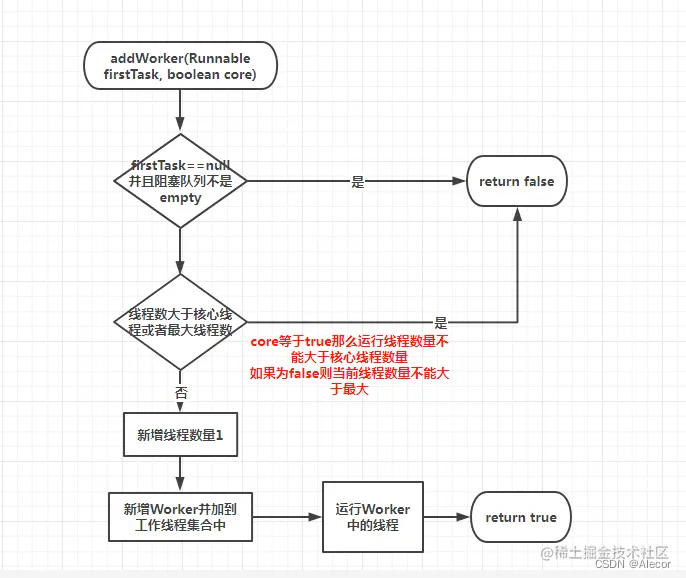
工作中几个问题的思考
对于需要并行多公司并行处理的任务,方案是什么? 多线程、并行流、并发库(ExecutorService、Futrue、Callable),分布式计算(1)按照公司ID分片 (2)按照业务类型分片 处理…...
Jmeter的性能测试
性能测试的概念 定义:软件的性能是软件的一种非功能特性,它关注的不是软件是否能够完成特定的功能,而是在完成该功能时展示出来的及时性。 由定义可知性能关注的是软件的非功能特性,所以一般来说性能测试介入的时机是在功能测试…...
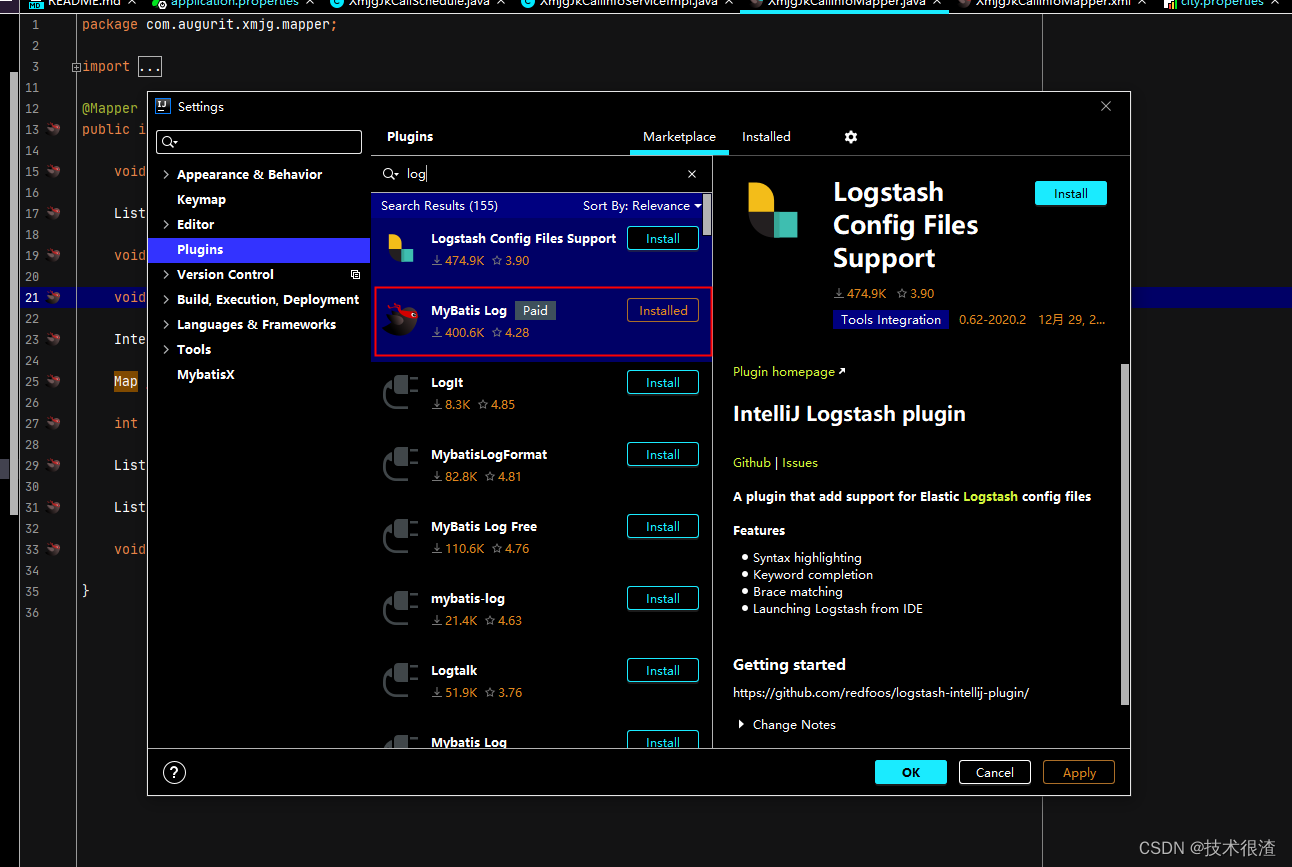
IntelliJ IDEA 2020.2.1白票安装使用方法
先安装好idear Plugins 内手动添加第三方插件仓库地址:https://plugins.zhile.io 搜索:IDE Eval Reset插件进行安装 输入https://plugins.zhile.io 手动安装离线插件方法 安装包可以去笔者的CSDN资源库下载 安装mybaties插件...

【UCAS自然语言处理作业一】利用BeautifulSoup爬取中英文数据,计算熵,验证齐夫定律
文章目录 前言中文数据爬取爬取界面爬取代码 数据清洗数据分析实验结果 英文数据爬取爬取界面动态爬取 数据清洗数据分析实验结果 结论 前言 本文分别针对中文,英文语料进行爬虫,并在两种语言上计算其对应的熵,验证齐夫定律github: ShiyuNee…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
