机器学习中的核方法

一、说明
线性模型很棒,因为它们易于理解且易于优化。他们受苦是因为他们只能学习非常简单的决策边界。神经网络可以学习更复杂的决策边界,但失去了线性模型良好的凸性特性。
使线性模型表现出非线性的一种方法是转换输入。例如,通过添加特征对作为附加输入。在这种表示上学习线性模型是凸的,但在除了非常低维的空间之外的所有空间中,计算量都是令人望而却步的。有人可能会问:是否可以保留原始数据表示,而不是显式扩展特征空间,并且所有特征都会破坏隐式?令人惊讶的是,答案通常是“是”,而使这成为可能的技术系列被称为内核方法。
二、从特征组合到内核
增加线性模型表达能力的一种方法是爆炸特征空间。例如,“二次”特征爆炸可能会将特征向量x = <x_1, x_2,x_3,…,x_D> 映射到表示为 φ(x) 的扩展版本:
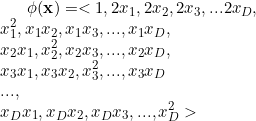
然后我们可以在扩展的特征空间上训练分类器。这样做有两个主要问题。第一个是计算性的:如果您的线性算法在特征数量上线性扩展,那么您只需对需要执行的计算量进行平方即可;您还计算了所需内存量的平方。第二个是统计方面的:如果您按照启发式,每个特征应该有大约两个示例,那么您现在将需要二次方数量的训练示例,以避免过度拟合。
我们将在这篇文章中尝试解决计算问题。
基于内核的学习的关键见解是,您可以以不需要显式计算 φ( x) 的方式重写许多线性模型。首先,您可以将其视为纯粹的计算“技巧”,使您能够使用二次特征映射的强大功能,而无需实际计算和存储映射向量。稍后你会发现它更深一些。我们讨论的大多数算法在执行特征映射后都涉及w · φ( x )形式的乘积。目标是重写这些算法,以便它们只依赖于两个示例(例如x和z)之间的点积;即,它们取决于 φ( x ) · φ( z )。要理解为什么这很有用,请考虑上面的二次展开和两个向量之间的点积。你得到:
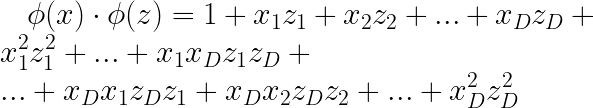

![]()
![]()
因此,计算 φ( x ) · φ( z ) 所需的时间与计算x · z所用的时间完全相同(加上执行加法和乘法所需的时间)。
其余的实际挑战是重写算法,以便它们依赖于示例之间的点积,而不是任何显式的权重向量。
三、核化感知器
让我们考虑上一篇文章中的原始感知器算法,这里使用线性代数符号和特征扩展符号 φ(x ) 进行重复。
PerceptronTrain(D,MaxIter) w <- 0 // initialize weights
b <- 0 // initialize bias
for iter=1 to MaxIter dofor all (x,y) ∈ D doa ← w · φ( x) + b // compute activation for this exampleif ya <= 0 thenw ← w + y φ(x ) // update weightsb <- b + y // update bias endifendfor
endfor
return w, b 在这个算法中,有两个地方明确使用了φ( x ) 。第一个是计算激活(第 4 行),第二个是更新权重(第 6 行)。目标是消除该算法对 φ 和权重向量的显式依赖。
为此,您可以观察到在算法中的任何点,权重向量w都可以写成扩展训练数据的线性组合。特别是,在任意点,对于某些参数 α, w = Σ α_nφ(x_n)。最初,w = 0,因此选择α = 0 会产生此结果。如果第一次更新发生在第 n 个训练样本上,则分辨率权重向量就是 y_n φ(x_n),相当于设置 α_n = y_n。如果第二次更新发生在第 m 个训练样本上,那么您所需要做的就是更新 α_m ← α_m + y_m。这一观察结果引出了以下表示定理,该定理指出感知器的权重向量位于训练数据的范围内。
感知器表示定理:在感知器算法运行期间,权重向量w始终位于(假设非空)训练数据φ(x_1 ), 的范围内。。。, φ (x_N)。
证明。通过归纳法。基本情况:任何非空集的跨度都包含零向量,即初始权重向量。归纳情况:假设定理在第 k 次更新之前为真,并假设第 k 次更新发生在示例 n 上。根据归纳假设,可以在更新前写出w = Σ α_i φ(x_i) 。新的权重向量为 [Σ α_i φ(x_i )] + y_n φ( x_n ) = Σ (α_i + y_n [ i = n])φ (x_i ),仍然在训练数据的范围内。
并不是说我们知道对于某些 α_is 总是可以写出w = Σα_nφ(x_n),我们还可以将激活(第 4 行)计算为:
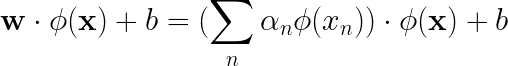

现在,这仅取决于数据点之间的点积,并且从不明确需要权重向量。您现在可以重写整个感知器算法,以便它永远不会明确引用权重,而仅依赖于示例之间的成对点积
这种“核化”算法的优点是,您可以“免费”执行特征扩展,例如简介中的二次特征扩展。例如,对于与二次特征完全相同的成本,您可以使用三次特征图,计算为 φ( ̈ x)φ(z) = (1 + x · z)³,它对应于变量之间的三向交互。(而且,一般来说,您可以在相同的计算复杂度下对任何多项式次数 p 执行此操作。)
四、什么构成了内核?
内核只是广义点积的一种形式。您也可以将其视为 φ( x ) · φ( z ) 的简单简写。这通常称为xa和z之间的内核乘积。
从这个角度来看,我们在上一节中看到的是,您可以重写感知器算法(这同样适用于许多其他算法),以便它们仅依赖于数据点之间的内核乘积,而不依赖于实际数据点他们自己。这是一个非常强大的概念,因为它使得大量非线性算法的开发基本上“免费”(通过应用所谓的内核技巧)。
4.1 核函数的特点
机器学习(包括 SVM(支持向量机))中使用的核函数具有几个重要特征,包括:
- Mercer 条件:核函数必须满足 Mercer 条件才有效。这个条件确保核函数是半正定的,这意味着它总是大于或等于零。
- 正定性:如果核函数始终大于零(除非输入彼此相等),则该核函数是正定的。
- 非负性:核函数是非负的,这意味着它为所有输入生成非负值。
- 对称性:核函数是对称的,这意味着无论输入的顺序如何,它都会产生相同的值。
- 再现性:如果核函数可以用来重建特征空间中的输入数据,则它满足再现性。
- 平滑度:如果核函数能够将输入数据平滑地变换到特征空间,则称该核函数是平滑的。
- 复杂性:核函数的复杂性是一个重要的考虑因素,因为更复杂的核函数可能会导致过度拟合并降低泛化性能。
基本上,核函数的选择取决于具体问题和数据的特征,选择合适的核函数可以显着影响机器学习算法的性能。
4.2 内核函数
核是用于将原始输入数据点映射到高维特征空间的数学函数,因此,即使数据点在原始输入空间中不是线性可分的,也可以轻松找到超平面。一些常见的核函数包括线性核函数、多项式核函数、径向基函数 (RBF) 和 sigmoid 核函数。
标准核函数方程:
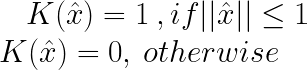
高斯核:
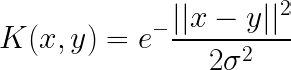
高斯核用于在没有数据先验知识的情况下执行变换。
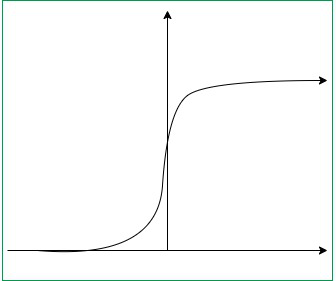
sigmoid函数:
该函数相当于神经网络的第二层感知器模型l,用作人工神经元的激活函数。
![]()
五、结论
弗朗西斯科·佛朗哥
相关文章:

机器学习中的核方法
一、说明 线性模型很棒,因为它们易于理解且易于优化。他们受苦是因为他们只能学习非常简单的决策边界。神经网络可以学习更复杂的决策边界,但失去了线性模型良好的凸性特性。 使线性模型表现出非线性的一种方法是转换输入。例如,通过添加特征…...
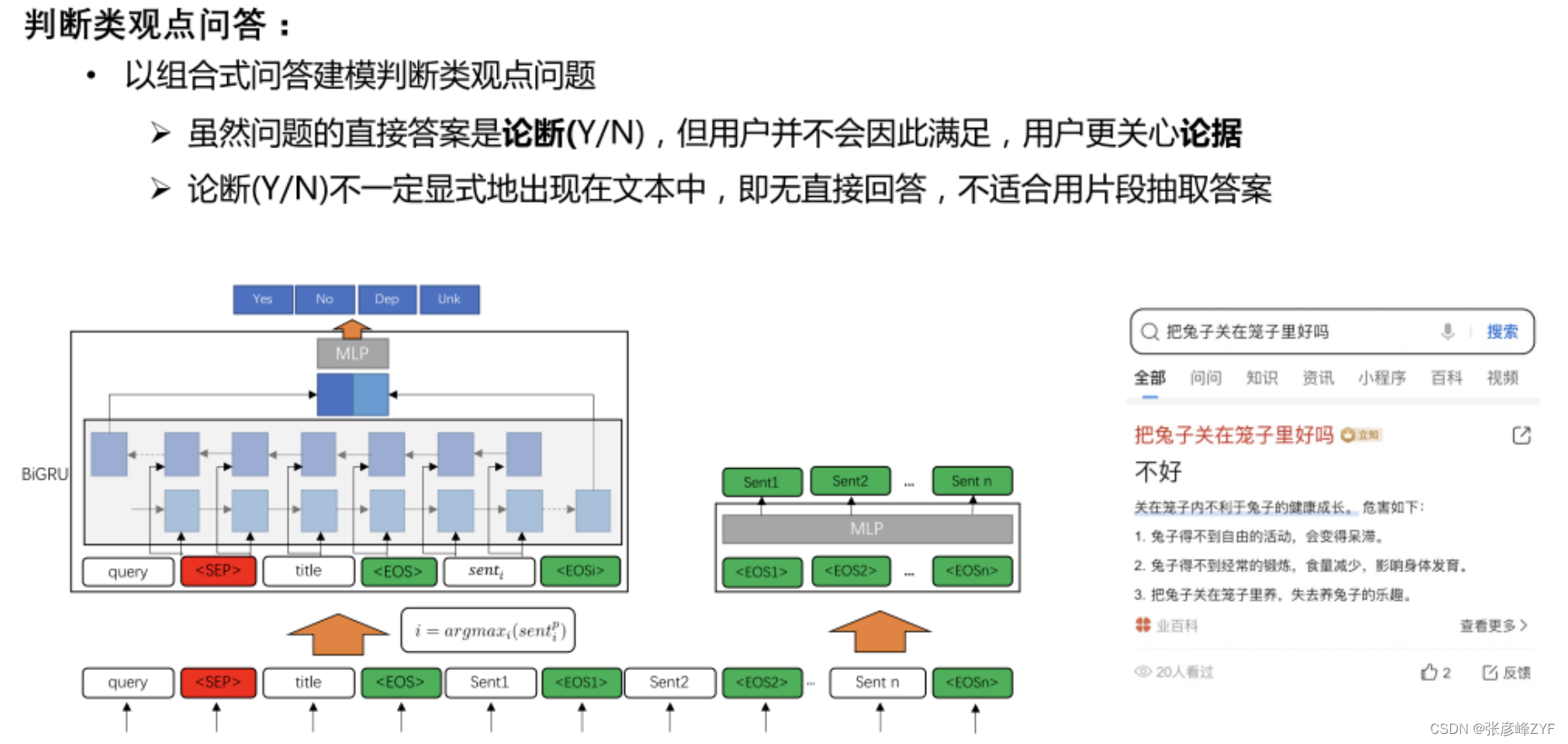
搜索问答技术学习:基于知识图谱+基于搜索和机器阅读理解(MRC)
目录 一、问答系统应用分析 二、搜索问答技术与系统 (一)需求和信息分析 问答需求类型 多样的数据源 文本组织形态 (二)主要问答技术介绍 发展和成熟度分析 重点问答技术基础:KBQA和DeepQA KBQA(…...
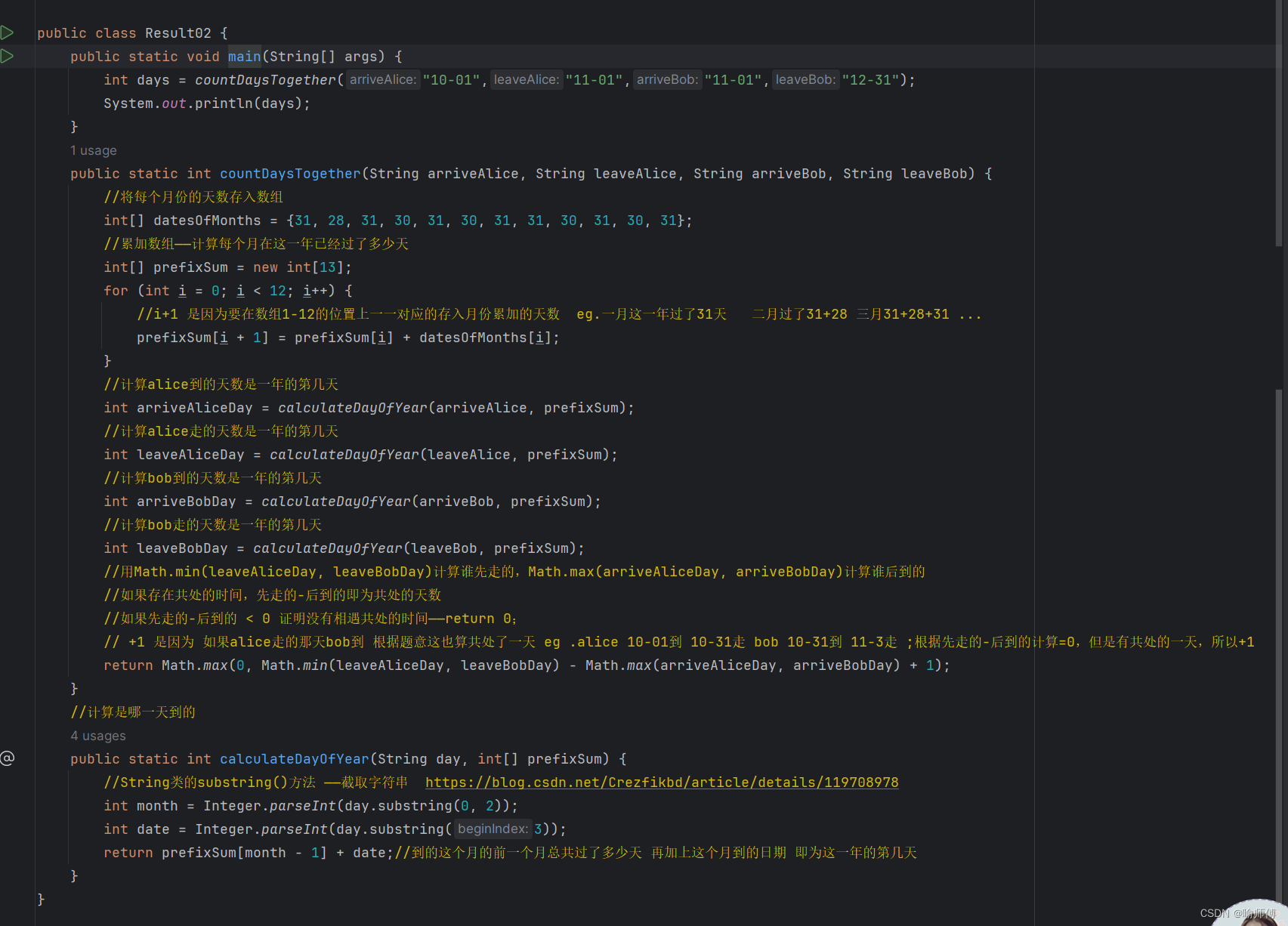
LeetCode2409——统计共同度过的日子数
博主的解法过于冗长,是一直对着不同的案例debug修改出来的,不建议学习。虽然提交成功了,但是自己最后都不知道写的是啥了哈哈哈。 package keepcoding.leetcode.leetcode2409; /*Alice 和 Bob 计划分别去罗马开会。给你四个字符串 arriveA…...

【MyBatisPlus】快速入门、常用注解、常用配置
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 MyBatisPlus 一、快速入门1.1 引入MyBatisP…...

【USRP】通信之:光通信
光通信: 光通信是使用光信号(通常是红外或可见光信号)在光纤或空气中传输信息的技术。由于光信号的特性,光通信具有非常高的数据传输率和长距离传输能力。以下是光通信的一些关键组件和概念: 光纤: 是由非常纯净的玻璃…...

bpf对内核的观测
目录 1 bpftrace常用命令1.1 列出bpftrace 相关命令的list1. 2bpftrace -e 是执行1.3 查看参数 -lv 2 bpftrace 可以用到的变量3 高级3.1 内置函数3.2 文件系统3.3 内核内存 栈3.4 Malloc 调用 统计3.5 系统调用 brk 的 统计3.6 脚本调用 4 应用5 怎么串联起来呢 bpftrace 总的…...

Tiktok shop api 调试
记录一下调试Tiktok shop api 踩坑记录。 主要是在按官网api上规则和加密生成sign时候一直通不过的问题: 官网地址:https://partner.tiktokshop.com/doc/page/63fd743e715d622a338c4eab 直接贴代码了 import lombok.extern.slf4j.Slf4j;import javax.cr…...

QFSFileEngine::open: No file name specified解决方案
问题 使用QFile类进行文件操作时,报错QFSFileEngine::open: No file name specified。 原因 QFile::open: No file name specified是Qt中的一个错误消息,提示没有指定文件名导致文件无法打开。这个错误通常出现在使用QFile::open()函数时没有提供有效…...

Flappy bird项目
一、功能分析 1、小鸟自动向右滑行 2、按下空格小鸟上升,不按下落 3、显示小鸟需要穿过的管道 4、管道自动左移和创建 5、小鸟和管道碰撞,游戏结束 6、技术 7、 项目框图 8、Ncurses 1)创建窗口界面,移动光标,产…...

高校教务系统登录页面JS分析——西安科技大学
高校教务系统密码加密逻辑及JS逆向 本文将介绍高校教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习,勿用于非法用途。 一、密码加…...

Mysql 事务的实现原理
Mysql 里面的事务,满足 ACID 特性,所以Mysql 的事务实现原理,就是InnoDB 是如何保证 ACID 特性的。 ACID A 表示 Atomic 原子性,也就是需要保证多个 DML 操作是原子的,要么都成功,要么都失败。那么…...
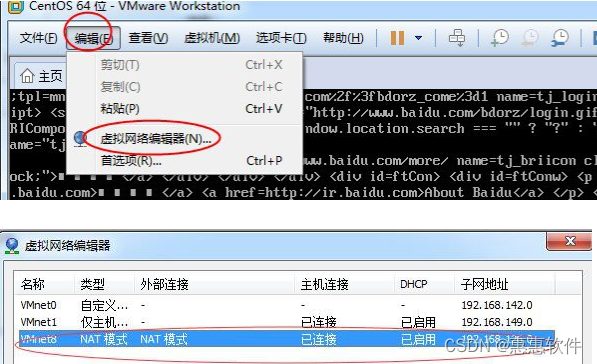
使用vscode搭建虚拟机
首先vscode插件安装 名称: Remote - SSH ID: ms-vscode-remote.remote-ssh 说明: Open any folder on a remote machine using SSH and take advantage of VS Codes full feature set. 版本: 0.51.0 VS Marketplace 链接: https://marketplace.visualstudio.com/items?it…...

C# 使用 LibUsbDotNet 实现 USB 设备检测
国庆节回来后的工作内容,基本都在围绕着各种各样的硬件展开,这无疑让本就漫长的 “七天班” ,更加平添了三分枯燥,我甚至在不知不觉中学会了,如何给打印机装上不同尺寸的纸张。华为的 Mate 60 发布以后,人群…...

系统安全分析与设计
系统安全分析与设计(2分) 内容提要 对称加密与非对称加密 加密技术与认证技术 加密技术(只能防止第三方窃听) 讲解地址:对称加密与非对称加密_哔哩哔哩_bilibili 认证技术 骚戴理解:数字签名是用私钥签名…...
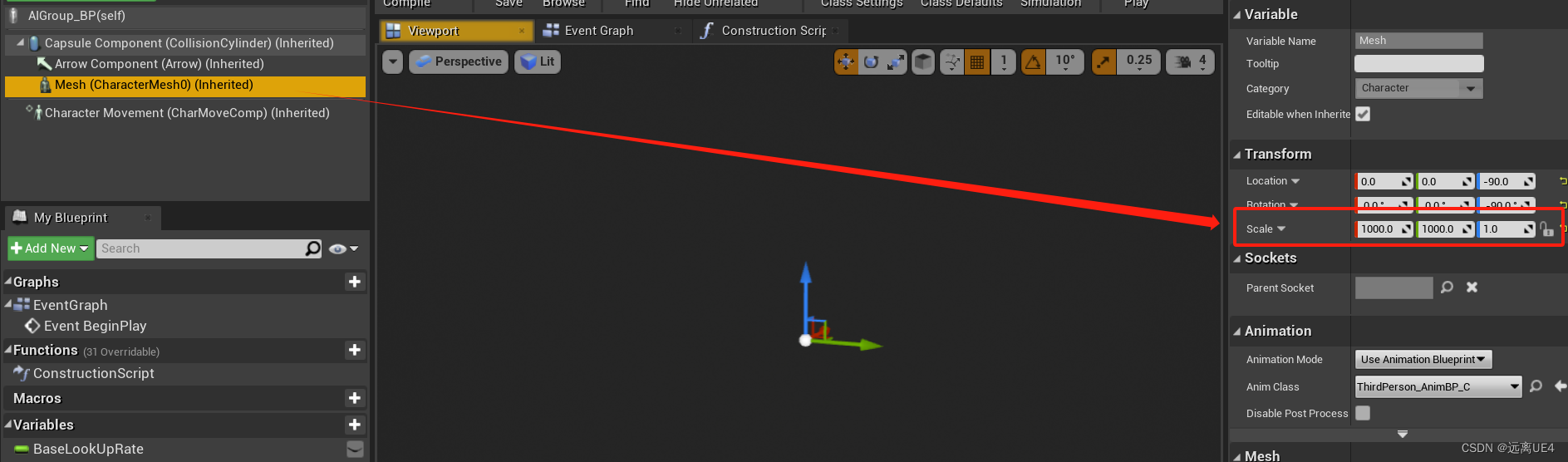
UE4 AI群集实现
逻辑就不用说了,就是计算对应图形位置让每个Pawn移动到该位置 因为有时候AI与AI会卡住 所以加上这个Bool为true,以及设置两个AI之间至少隔的距离,设置在一个合理的参数即可 有时候AI群集,AI与AI会比较紧密,可以将Caps…...
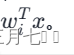
机器学习---CNN(创建和训练一个卷积神经网络并评估其性能)下
import numpy as np import matplotlib.pyplot as plt from cnn_operations import cnn_operations as cnn_opr convolutional_neural_network模块: 1. 卷积神经网络类 def __init__(self):# 网络的层数self.n_layers 0# list,网络中的各层self.layers…...
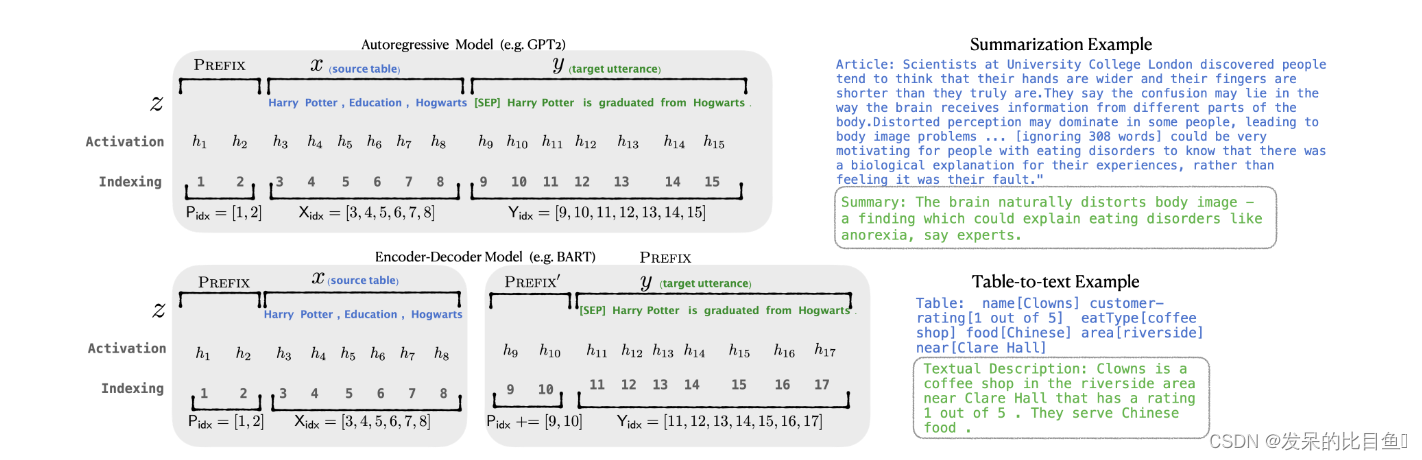
2021-arxiv-Prefix-Tuning- Optimizing Continuous Prompts for Generation
2021-arxiv-Prefix-Tuning- Optimizing Continuous Prompts for Generation Paper:https://arxiv.org/pdf/2101.00190.pdf Code:https://github.com/XiangLi1999/PrefixTuning 前缀调优:优化生成的连续提示 prefix-tunning 的基本思想也是想…...

使用CMakeLists.txt简化项目构建过程
在软件开发过程中,项目的构建是一个不可避免的环节。而随着项目规模的增大,手动管理编译过程变得越来越繁琐。为了简化构建流程并实现跨平台支持,CMake作为一种流行的构建系统被广泛采用。本文将介绍CMakeLists.txt文件的结构,以及…...

构建并训练简单的CNN
1. 构建并训练深度神经网络模型 1.1 准备数据集 本次使用自己生成的一些数据,如下生成代码: # 准备数据集 # 此处自己生成一些原始的数据点 dataset_X=np.linspace(-10,10,100) dataset_y=2*np.square(dataset_X)+7...

Axi_Lite接口的IP核与地址与缓冲与AxiGP0
AXI Interconnect互连内核将一个或多个 AXI 内存映射主设备连接到一个或多个内存映射从设备。 AXI_GP 接口 AXI_GP 接口是直接连接主机互联和从机互联的端口的。 AXI_HP 接口具有一个 1kB 的数据 FIFO 来做缓冲 [4],但是 AXI_GP 接口与它不同,没…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
