第 368 场 LeetCode 周赛题解
A 元素和最小的山形三元组 I

前后缀操作:求出前后缀上的最小值数组,然后枚举 j j j
class Solution {
public:int minimumSum(vector<int> &nums) {int n = nums.size();vector<int> l(n), r(n);//l[i]=min{nums[0],...,nums[i]}, r[i]=min{nums[i],...,nums[n-1]}l[0] = nums[0];for (int i = 1; i < n; i++)l[i] = min(l[i - 1], nums[i]);r[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--)r[i] = min(r[i + 1], nums[i]);int res = INT32_MAX;for (int j = 1; j < n - 1; j++)if (l[j - 1] < nums[j] && r[j + 1] < nums[j])res = min(res, l[j - 1] + nums[j] + r[j + 1]);return res == INT32_MAX ? -1 : res;}
};
B 元素和最小的山形三元组 II

同 A …
class Solution {
public:int minimumSum(vector<int> &nums) {int n = nums.size();vector<int> l(n), r(n);//l[i]=min{nums[0],...,nums[i]}, r[i]=min{nums[i],...,nums[n-1]}l[0] = nums[0];for (int i = 1; i < n; i++)l[i] = min(l[i - 1], nums[i]);r[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--)r[i] = min(r[i + 1], nums[i]);int res = INT32_MAX;for (int j = 1; j < n - 1; j++)if (l[j - 1] < nums[j] && r[j + 1] < nums[j])res = min(res, l[j - 1] + nums[j] + r[j + 1]);return res == INT32_MAX ? -1 : res;}
};
C 合法分组的最少组数

枚举:枚举分组中有最多下标的组的下标数 i i i ,设一个数 v a l val val 在 n u m s nums nums 的出现次数为 c i ci ci ,若 v a l val val 可以满足条件的被分为若干组,则有 c i = a × i + b × ( i − 1 ) , a ≥ 0 , b ≥ 0 ci=a\times i+b\times(i-1), a\ge0,b\ge 0 ci=a×i+b×(i−1),a≥0,b≥0,等价于 c i = a b × i − b , a b ≥ b ≥ 0 ci=ab\times i - b,ab\ge b\ge0 ci=ab×i−b,ab≥b≥0,即 ⌈ c i i ⌉ ≥ ⌈ c i i ⌉ × i − c i \left \lceil \frac {ci} i \right \rceil \ge \left \lceil \frac {ci} i \right \rceil\times i-ci ⌈ici⌉≥⌈ici⌉×i−ci
class Solution {
public:int minGroupsForValidAssignment(vector<int> &nums) {unordered_map<int, int> cnt;for (auto x: nums)cnt[x]++;unordered_map<int, int> can;int m = cnt.size();//nums中不同的数val的个数for (auto &[_, ci]: cnt) {for (int i = 1; i <= ci + 1; i++) {int ab = (ci - 1) / i + 1;int b = ab * i - ci;if (ab >= b)can[i]++;}}int mx = 1;for (auto &[gs, ci]: can)if (ci == m)//对nums中每个数val都可以划分为若干大小为gs-1和若干大小为g的组mx = max(mx, gs);int res = 0;for (auto &[_, ci]: cnt)res += (ci - 1) / mx + 1;return res;}
};
D 得到 K 个半回文串的最少修改次数

动态规划:首先需要预处理求出 c o s t cost cost 数组( c o s t [ i ] [ j ] cost[i][j] cost[i][j] 为将字符串 s [ i , j ] s[i,j] s[i,j] 修改为半回文串的最少修改次数),然后设 p [ i ] [ j ] p[i][j] p[i][j] 为使 s [ 0 , i ] s[0,i] s[0,i] 可分为 j j j 个半回文串的最少操作数,枚举其第 j j j 个半回文串可能的长度来进行状态转移
class Solution {
public:vector<vector<int>> cost;string s;int n;void comp_cost(int i, int j, int d) {//以d为模数(题目描述中的d)更新cost[i][j]int g = (j - i + 1) / d;//分组大小int tot = 0;for (int ind = 0; ind < d; ind++) {//枚举d个分组,若s[i,j]是半回文串则每个分组都是回文串for (int l = i + ind, r = i + ind + d * (g - 1); l <= r; l += d, r -= d)if (s[l] != s[r])tot++;}cost[i][j] = min(cost[i][j], tot);//更新cost[i][j]}int minimumChanges(string s, int k) {this->s = s;n = s.size();cost = vector<vector<int>>(n, vector<int>(n, INT32_MAX));for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {//s[i,j]int len = j - i + 1;for (int d = 1; d * d <= len; d++)if (len % d == 0) {//len的因子dcomp_cost(i, j, d);if (d != len / d && d != 1)//len的因子len/dcomp_cost(i, j, len / d);}}}int p[n][n + 1];// loc, kfor (int i = 0; i < n; i++)for (int j = 0; j <= n; j++)p[i][j] = INT32_MAX;//无效状态标志for (int i = 1; i < n; i++) {for (int j = 1; j <= (i + 1) / 2; j++) {if (j == 1)p[i][j] = cost[0][i];for (int pre = 0; i - pre > 1; pre++)if (p[pre][j - 1] != INT32_MAX)p[i][j] = min(p[i][j], p[pre][j - 1] + cost[pre + 1][i]);//考虑最后一个半回文串为s[pre+1][i]的情况}}return p[n - 1][k];}
};
相关文章:

第 368 场 LeetCode 周赛题解
A 元素和最小的山形三元组 I 前后缀操作:求出前后缀上的最小值数组,然后枚举 j j j class Solution { public:int minimumSum(vector<int> &nums) {int n nums.size();vector<int> l(n), r(n);//l[i]min{nums[0],...,nums[i]}, r[i]mi…...

Qt中QFile、QByteArray QDataStream和QTextStream区别及示例
在Qt中,QFile、QByteArray、QDataStream和QTextStream是常用的文件和数据处理类。 主要功能和区别 QFile: QFile是用于读写文本和二进制文件以及资源的I/O设备。可以单独使用QFile,或者更方便地与QTextStream或QDataStream一起使用。 通常在…...

【操作系统】32进制小数转16进制
要将32进制的小数转换为16进制,可以按照以下步骤进行: 将32进制小数转换为10进制。可以使用上述提到的方法,将32进制小数转换为对应的10进制数。 将10进制数转换为16进制。使用常规的方法将10进制数转换为16进制数。可以将10进制数不断除以1…...
C#实现数据导出任一Word图表的通用呈现方法及一些体会
疲惫的修改 应人才测评产品的需求,导出测评报告是其中一个重要的环节,报告的文件类型也多种多样,其中WORD输出也扮演了一个重要的角色。 实现方法比较简单,结合分析结果数据,通过WORD模板文件进行替换输出。在实现的…...

2023-10 字节跳动面试整个过程 golang营销服务开发岗位
面试整个过程大约1个小时回答的中规中矩吧 很多问题回答的不具体 难受死我了非常简单的算法题下面列出来了面试步骤这里面有一点就是面试官本来想问问我数据结构这一块的问题 但是我说不太熟悉 他就没问了 1. 简单介绍个人信息 略2. 介绍简历上的项目 略3. 什么是分布式事务 主…...

Java类名的命名规范
Java中的类名必须以字母或者下划线开头,不能以数字开头。 类名的每个单词的首字母必须大写,这被称为帕斯卡命名法。 此外,类名不能使用关键字或保留字,不能使用数字除了_和$之外的任何符号,中间不能添加空格。 如果…...
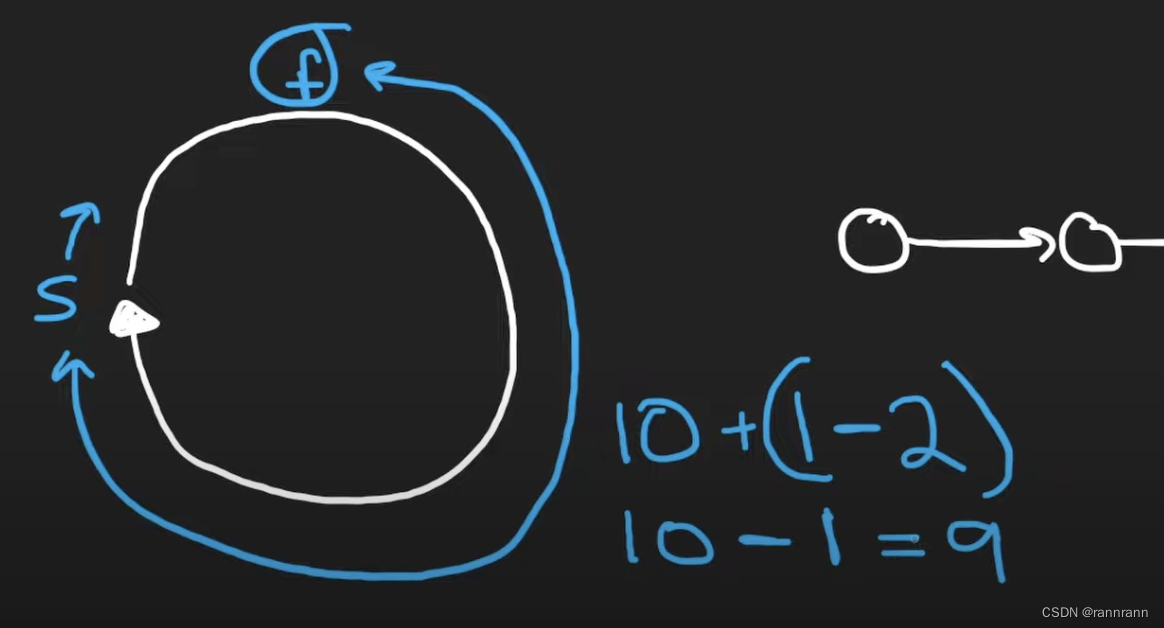
【c++Leetcode】141. Linked List Cycle
问题入口 思想:Floyds Tortoise and Hare 这个算法简单来说就是设置一个慢指针(一次移动一个位置)和一个快指针(一次移动两个位置)。在遍历过程中,如果慢指针和快指针都指向同一个元素,证明环…...
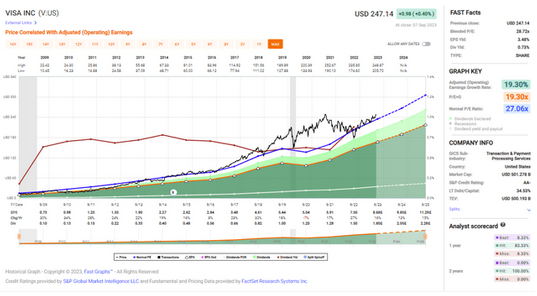
Visa股票仍然值得投资
来源:猛兽财经 作者:猛兽财经 总结: (1)尽管Visa(V)的估值高于市场平均水平,但仍值得买入。 (2)Visa拥有强劲的基本面,销售额和每股收益一直在稳定增长,股息…...

【Android知识笔记】RecyclerView专题
RecyclerView工作流程 RecyclerView 的使用方法简单回顾: // 1. 添加gradle依赖 implementation androidx.recyclerview:recyclerview:1.1.0// 2. 布局文件 <?xml version="1.0" encoding="utf-8"?> <FrameLayout xmlns:android="http:…...
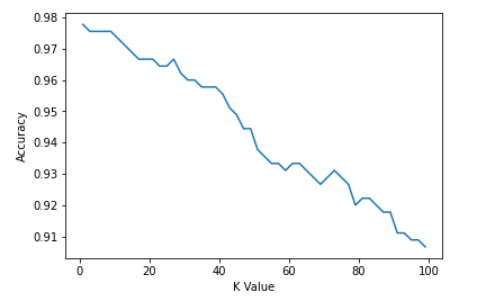
从头开始使用 KNN 进行 KNN 和 MNIST 手写数字识别的初学者指南
一、说明 MNIST (“修改后的国家标准与技术研究所”)是事实上的计算机视觉“hello world”数据集。自 1999 年发布以来,这个经典的手写图像数据集一直作为分类算法基准测试的基础。随着新的机器学习技术的出现,MNIST 仍然是研究人…...
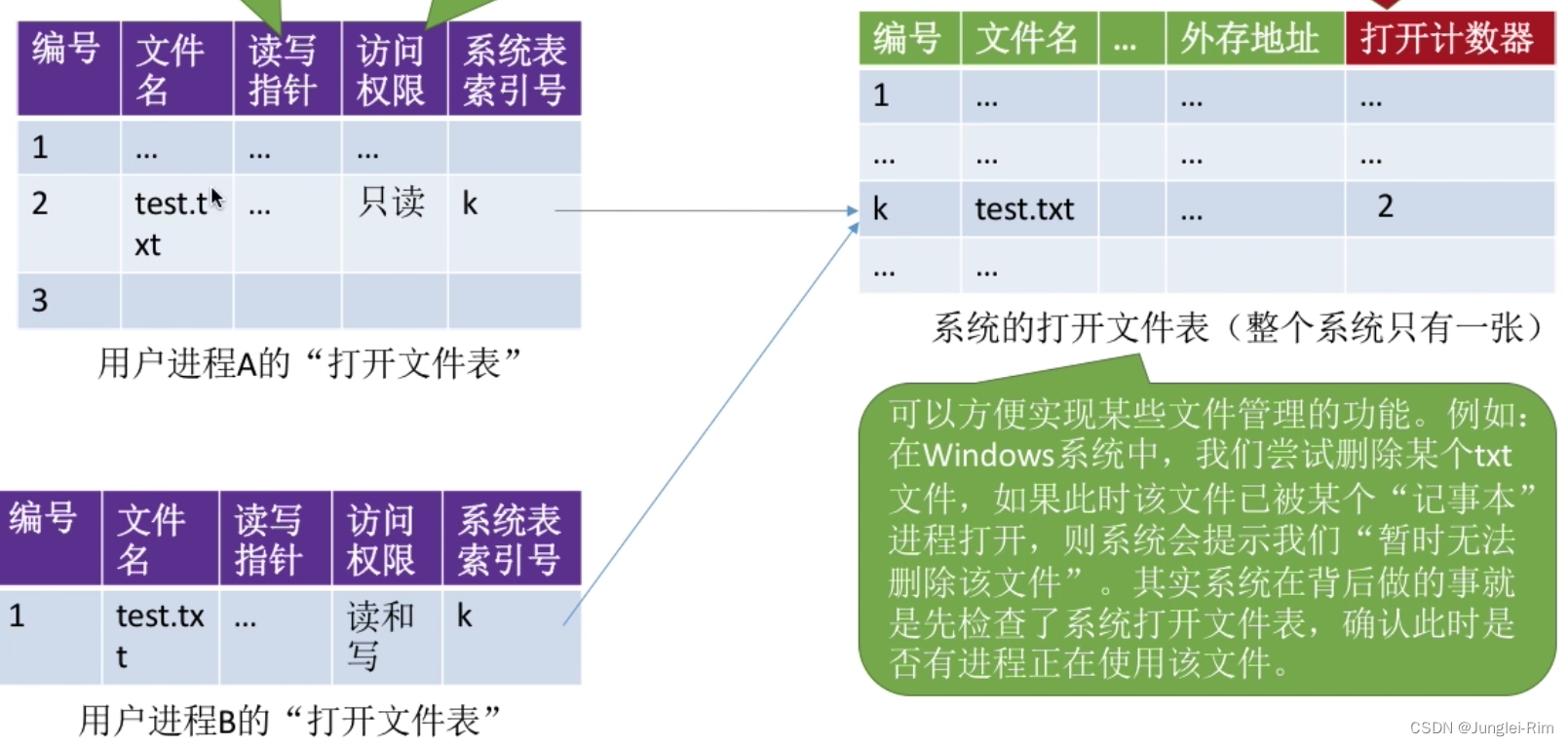
文件的基本操作(创建文件,删除文件,读写文件,打开文件,关闭文件)
1.创建文件(create系统调用) 1.进行Create系统调用时, 需要提供的几个主要参数: 1.所需的外存空间大小(如:一个盘块,即1KB) 2.文件存放路径(“D:/Demo”) 3.文件名(这个地方默认为“新建文本文档.txt”) …...

微积分(二) 导数与微分
前言 导数反映了函数值相对于自变量的变化快慢程度,而微分则表明当自变量有微小变化时,函数值大体上变化多少 瞬时速度的解决——极限 牛顿采用了一种无限逼近的方法。 平均速度的定义:如果一个物体在一段时间△t内位移了s,它在这段时间内的平均速度…...
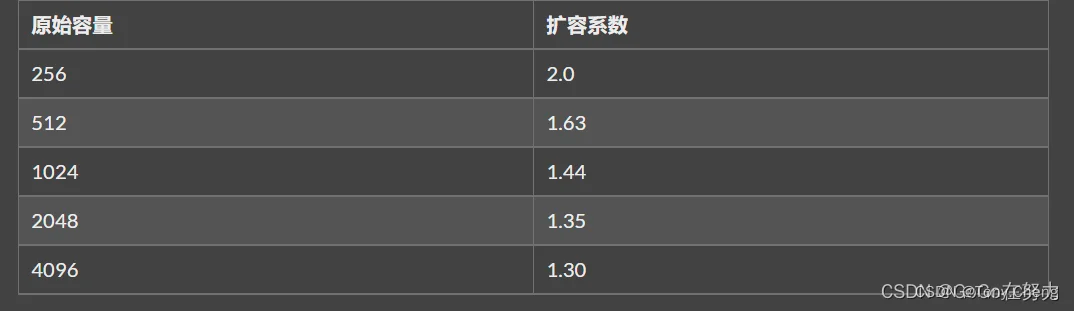
go语言Array 与 Slice
有的语言会把数组用作常用的基本的数据结构,比如 JavaScript,而 Golang 中的数组(Array),更倾向定位于一种底层的数据结构,记录的是一段连续的内存空间数据。但是在 Go 语言中平时直接用数组的时候不多,大多数场景下我…...

Ubuntu自启动设置
ubuntu中编写shell脚本开机自动启动(推荐)_Linux_脚本之家 1. vim test.sh 2. #!/bin/bash ### BEGIN INIT INFO # Provides: test # Required-Start: $remote_fs $syslog # Required-Stop: $remote_fs $syslog # Default-Start: 2 3 4 5 # Default-Stop: 0 1 6 …...

Qwen 通义千问 14B 模型,长文本问答效果测试
千问的config: seq_len2k max_position_embedding8k 注意,以下实验结果的字数是token数,不是中文字符数。 不使用动态ntk 12000字输入: 乱码5000字输入:乱码1500字输入:正常 不使用动态ntk,…...

Prefix-Tuning源码解析
Prefix-Tuning源码解析 Prefix-Tuning在PEFT包中的源码实现 改写自Based on https://github.com/THUDM/P-tuning-v2/blob/main/model/prefix_encoder.py import torch from transformers import PretrainedConfigclass PrefixEncoder(torch.nn.Module):rThe torch.nn model t…...
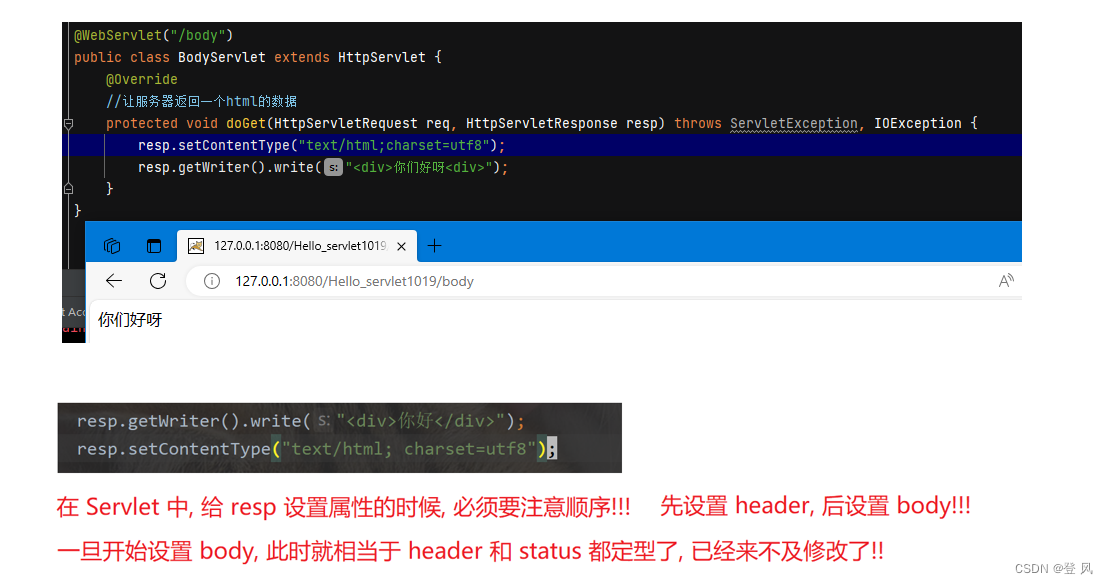
Java EE-servlet API 三种主要的类
上述的代码如下: import javax.servlet.ServletException; import javax.servlet.annotation.WebServlet; import javax.servlet.http.HttpServlet; import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletResponse; import java.i…...

简单谈谈我参加数据分析省赛的感受与体会
数据分析省赛的感受与体会 概要考试前的感受与体会考试注意事项小结 概要 大数据分析省赛指的是在省级范围内举办的大数据分析竞赛活动。该竞赛旨在鼓励和推动大数据分析领域的技术创新和人才培养,促进大数据技术与应用的深度融合,切实解决实际问题。参…...
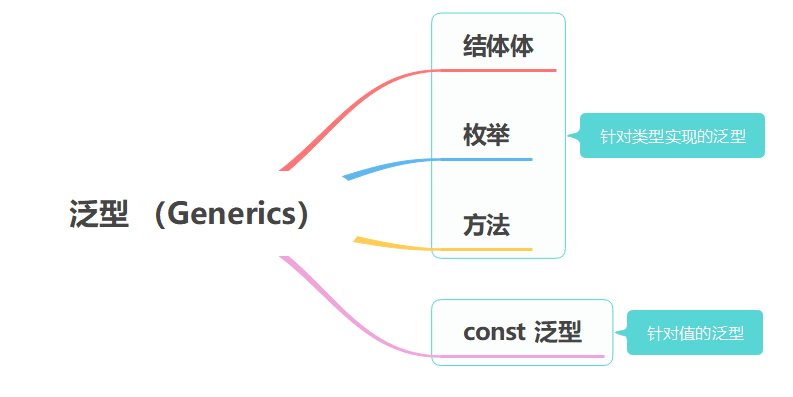
rust学习——泛型 (Generics)
文章目录 泛型 Generics泛型详解结构体中使用泛型枚举中使用泛型方法中使用泛型为具体的泛型类型实现方法 const 泛型(Rust 1.51 版本引入的重要特性)const 泛型表达式 泛型的性能 泛型 Generics Go 语言在 2022 年,就要正式引入泛型…...

【USRP】通信之有线通信
有线通信: 有线通信是指使用物理线路或媒体(例如,铜线、同轴电缆、光纤)进行数据、声音和视频传输的通信方式。由于它依赖于实体传输媒介,有线通信通常具有较高的稳定性和可靠性,并能支持长距离的高带宽通…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
