【算法练习Day26】分发饼干摆动序列 最大子数组和

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 分发饼干
- 摆动序列
- 最大子数组和
- 总结:
本期开始新的篇章,贪心算法题目的讲解。
贪心算法,没有固定的套路,通常根据做题人的做题经验,才能写出贪心算法。且算法有难度,并不总是简单的。贪心算法是一种常识思想,需要在做题中慢慢感觉和领悟。
分发饼干
455. 分发饼干 - 力扣(LeetCode)
分发饼干,是一道贪心算法的启蒙题(但是实际上我三道题都未能自己做出来,对贪心算法一无所知)。

题目大意是将一些饼干分发给一些小孩子们,小孩子们胃口各不相同,且每个孩子只能喂食一块饼干,要求是饼干的尺寸大于等于孩子的胃口值,求最多可以使几个孩子吃饱?解题的思路是我们可以创建一个变量count来记述我们已经满足了几个孩子,然后将孩子数组和饼干数组分别排序,使它们变得有序方便操作,用一个循环控制两个变量,当满足时候让饼干下标和孩子下标分别往后走,count自增,不满足只让饼干下标向后走,这样的原因是两数组有序,那么满足这个孩子的饼干如果存在,那么只可能在后面的饼干,而如果连这个孩子都无法满足,那肯定后面的孩子也无法满足。这就是排序的好处,如果不排序,那一个孩子需要遍历全部饼干,同样也要遍历所有孩子,这样会严重影响代码效率,时间为O(N^2)。
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int count=0;for(int i=0,j=0;i<g.size()&&j<s.size();){if(s[j]>=g[i]){count++;i++;j++;continue;}j++;}return count;}
};
排序起初我没有想到,但是看了题解我想到了这种方法,代码看起来略显冗余,下面看一个思路一样但是代码却很精简也不用count来计数的方法。
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int index=0;for(int i=0;i<s.size();i++){if(index<g.size()&&g[index]<=s[i]){index++;}}return index;}
};
我们用index来代替count和小孩数组的下标,用i来代替饼干下标,核心的思路是相同的,保证不要越界,然后当饼干能够满足小孩,index就自增,怎么样是不是简洁了不少,而且还巧妙的用孩子下标做了返回值。
摆动序列
376. 摆动序列 - 力扣(LeetCode)

在做这道题时候特别懵,没有任何思路,看了题解也很懵,后来想了一阵才慢慢明白。
题的大意是求摆动序列,可以删除改定序列的若干个元素,最后构成一个摆动序列,摆动序列的定义是严格按照数字之间的差值,在正数和负数之间来回摆动。实现预判式的在一个序列里删除某些节点而达到拼成最大摆动序列是十分困难的。
我们给出另一种解题思路,让我们不用删除节点,却起到了删除节点的效果。具体做法为,将一个序列模拟成山峰和山谷的示意图,也就是说把这些数都画出来,看它们的拐向,我们只要拐向一次向上一次向下的那种,如果中间是连续向上或者向下亦或者是平的(两个相邻数相等)我们全都统统不要。那么如何知道中间要删除这些节点,然后还能将删除后的两段连上呢?这是十分巧妙的做法,我们先定义两个变量一个代表上一次两个数的差值,另一个代表的是现在的相邻两个数的差值,如果两个差值是有正负变化的(前一个差值是0现在的差值是大于0或者小于0的同样符合摆动,反过来也是),那么就将计数器加1,且上一个的差值被改成当前的,然后进行下一次的循环。
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size()<=1)return nums.size();int cur=0;int pre=0;int count=1;for(int i=0;i<nums.size()-1;i++){cur=nums[i+1]-nums[i];if((cur>0&&pre<=0)||(cur<0&&pre>=0)){count++;pre=cur;}}return count;}
};
还有一些细节,需要交代一下,首先我们知道如果有摆动序列,那么至少要有1个数据来组成该序列,所以我们count要从1开始起,这是很关键的,由于我们让count从1开始,那么有几个拐点直接加在一起,就是此时最大摆动序列的总长度,而为什么要将pre=cur写到if的里面呢?如果if没进去我们就不改写前一个差的数值?实际上我们可以通过模拟得知,这种写法和把它写到外面在一般的测试用例下,跑出来的答案是一样的
但是如果碰到了序列走势是向上–平–向上这种情况呢?这种情况把pre写在if的外面会使拐点多算一次,实际上我们摆动序列是2,这样算起来是3,所以不能这样写,摆动序列的定义不能连续向上,即使中间有平也不行,况且平本来就不算在内,这也是代码的关键所在,它模拟出了,我们在真实删除数据时,是如何将删除后两段又重新链接在一起了,由于判断摆动符合我们才改变pre的值,所以不符合时候它一直是上一次符合时候的差值,当再次符合时进入if我们才改动pre,这也就相当于联系起了删除中间节点后两个链条的连接,这里的代码虽然简短,但是每一步的思路,尤其重要,建议大家用心去体会其过程的巧妙之处。
最大子数组和
53. 最大子数组和 - 力扣(LeetCode)
求最大的子数组连续和,这道题的题目大意和题目名字相同,首先能想到的一种思路是暴力法,双for来解决问题,一个for循环控制数组起始位置遍历,一个控制终点,两层遍历后,找到最大子数组和是多少返回,这种方法貌似以前是可以通过的,但是现在不行了,直接提交这种暴力解法会提示超时,这道题同样我们也是可以用贪心来做出来的。
思路其实很简单,我们用sum来记录当前总和,再用一个变量result来记录我们历史记录中取到的最大值,和它作比较,比result大则与之交换,而贪的是如果sum小于0,直接sum=0再从当前位置向后与sum相加,再记录,而暴力解法中的数组结束位置,我们用每次的result判断来代替,每一次循环都判断一次也就相当于这一步骤了
class Solution {
public:int maxSubArray(vector<int>& nums) {int result=INT_MIN;int sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i];if(sum>result)result=sum;if(sum<0)sum=0;}return result;}
};
如果数据全是-1呢?那它会求得答案为0吗?肯定是不会的,自行调试便知道,在sum=0之前由于我们result取得是int里最小的数,我们先行进行交换使result=-1,然后sum=0后再加上-1,结果还是-1它不可能变成0,这也就是为什么要把sum+=数据写在前面,result=最小数,是为了避免有负数和的产生。
从以上三题中,我个人认为,求某个条件下的最大的某某数这类题,应该是可以考虑用贪心算法做一下的,除了第二题有些难想外,第一题和第三题实际上确实是“常识”类的解题思路,但是有时候确实没有做过的话,还是无法做得出来,重要的是多多积累和总结,第一题实际上我觉得最重要的是排序,没有排序我们不可能那么轻易的解出来,而不用遍历那么多的数据,第二题是运用峰值的巧妙之处,求取了最长的摆动序列数据个数,第三道题贪的是sum小于0立刻重新计数
为什么当它为负数时候,直接sum=0了却不从之前数组统计的下一个开始计数,而是直接从当前位置向后计数呢?因为之前的数相加时候我们已经用resul来记录了这一段数据中最大的数是多少,数据是要连续的遍历相加。还不懂,不妨举一个例子,例如数据整体序列为{-5,3,4,-8,5}我们知道最大子数组和肯定是5,那我们看前面,走到-5直接跳了出来,然后3+4-8才跳了出来,那你说4-8会比3+4-8还要大吗?
肯定不能,这是一种情况说明了如果前一个数和后一个数都是正数那么实际上从它的下一个位置开始走,不可能找得到比从刚才那个数还大的组合了,那有人会说如果前一个数是负数后一个数是正数不就能找的到了吗也同样的可以模拟如果还是{-5,3,4,-8,5}那样的话第一个-5遇到了后面直接sum=0了,如果是{-5,3,-2,7,5}那从3向后遍历的和实际上是比从正数7大的,很多时候我们都可以用模拟来解决问题。
总结:
今天我们完成了分发饼干、摆动序列、最大子数组和三道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day26】分发饼干摆动序列 最大子数组和
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 分发饼干摆动序列最大子数组…...

redis缓存击穿/穿透/雪崩面试回答
面试官:什么是缓存穿透 ? 怎么解决 ? 候选人: 嗯~~,我想一下 缓存穿透是指查询一个一定不存在的数据,如果从存储层查不到数据则不写入缓存,这将导致这个不存在的数据每次请求都要到 DB 去查询,可能导致…...

Jmeter性能测试 —— TPS拐点寻找
寻找TPS性能拐点1、准备脚本①在本地电脑调试Jmeter压测脚本 ②上传到压测机Jmeter所在的服务器 2、执行压力测试①执行压测脚本 jmeter –n –t xianchengzuse.jmx ②记录业务压测数据 3、监控服务器性能指标 ①监控CPU输入top命令 ②监控内存 free –m ③jstat监控sweep和…...

科技资讯|苹果穿戴新专利,表带、服装等织物可变身柔性屏幕或扬声器
根据美国商标和专利局(USPTO)本周公示的清单,苹果公司获得了一项新的技术专利,可以在 Apple Watch 表带、服装等物品上,引入基于织物的柔性扬声器。 根据专利描述,通过在织物中嵌入声学组件(例…...
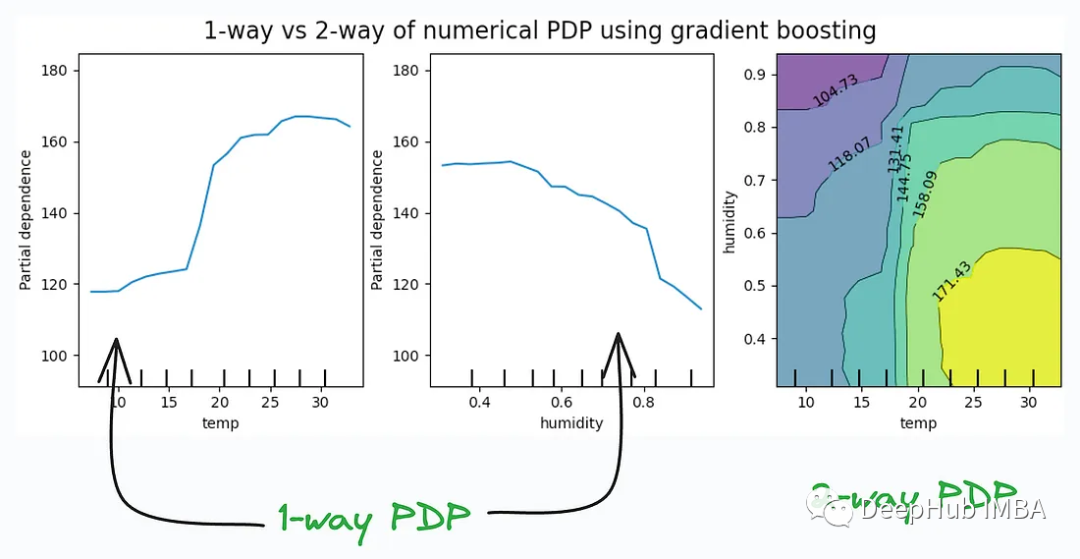
数据分析和机器学习的11个高级可视化图表介绍
可视化是一种强大的工具,用于以直观和可理解的方式传达复杂的数据模式和关系。它们在数据分析中发挥着至关重要的作用,提供了通常难以从原始数据或传统数字表示中辨别出来的见解。 可视化对于理解复杂的数据模式和关系至关重要,我们将介绍11…...
祝所有的程序猿们2023年的1024节快乐~
许久没更新Bolg了,眼看就要到1024节,其实也是没有可以更新的东西,目前在PhD,发现很多东西都还需要慢慢沉淀,放一doctoral college 开学的时候ppt的老图。 越往深处研究会陷入泥潭,考虑的细节将会越来越多&…...

Win10/Win11系统bitlocker正在等待激活如何解决?
有同学升级Win10系统后,发现C盘与D盘分区盘符中出现了黄色的锁定感叹号,还显示“bitlocker正在等待激活”,这可能是用户开启了bitlocker加密所导致的。下面就来看看解决的办法吧。 一、bitlocker正在等待激活的解决方法 打开控制面板-系统和安…...
酷开科技 | 酷开系统,为居家生活打开更精彩的窗口
电视在我们的日常生活中扮演着重要的角色。虽然,作为客厅C位的扛把子——电视的娱乐作用深入人心,但是,它的涵义和影响力却因我们每个人的具体生活环境而存在着种种差异,而我们的生活环境又受到我们所处的社会及文化环境的影响。 …...

谷歌真的不喜欢 Node.js ?
有人在 Quora 上提问,为什么谷歌不喜欢 Node.js 呢,Google 的 UX 工程师和来自 Node.js 团队的开发者分别回答了他们对这个问题的看法,对于编程语言来说,每一门语言都有它自己的优势,重要的是如何用它去解决问题。 谷…...

前端项目如何找到所有未被引用的文件
要找到 React 项目中所有未被引用的文件,可以使用工具来进行静态代码分析。以下是一些方法: 使用静态代码分析工具unimported: 静态代码分析工具可以找到未被引用的 JSX 文件。一个常用的工具是 “unimported”。以下是使用它的步骤ÿ…...

CANoe-使用IG Ethernet Packet Builder实现IP包分片的若干问题
在文章《CANoe-Ethernet IG和Ethernet Packet Builder的使用和区别》中,我们讲过Packet Builder可以组装多种类型的以太网报文: 当我们想组装一条icmpv4 echo request报文,payload只有1个字节的数据FF时,选择ICMPv4 Packet,创建一条ICMPv4报文,把payload改为1个字节: 然…...
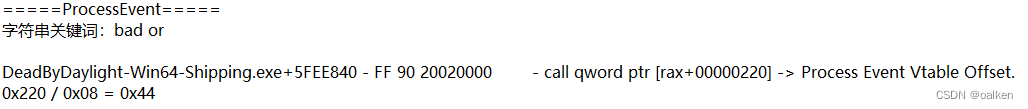
UE4逆向篇-2_各类数据的查找方式
写在前面 1.通过前面的文章,相信各位已经能够自己找到GNames并使用DUMP工具导出GNames了。 2.本篇文章将介绍各种所需数据的查找方法。 一、准备工作 1.CheatEngine,本篇以及后续篇幅的重要工具。 2.一个记事本,保证你能记录下关键信息。…...
)
JDBC-day07(Apache-DBUtils实现CRUD操作)
九:Apache-DBUtils实现CRUD操作 1 Apache-DBUtils简介 Apache-DbUtils 是 Apache 组织提供的开源 JDBC工具类库,它是对JDBC的简单封装,学习成本极低,并且使用DbUtils能极大简化JDBC编码的工作量,同时也不会影响程序的…...
零代码编程:用ChatGPT多线程批量将PDF文档转换为word格式
pdf2docx是Python的一个库,可以很方便的将PDF文档转换为word格式,首先安装这个库。 然后在ChatGPT中输入提示词: 你是一个Python编程专家,要完成一个文档格式转换的任务,具体步骤如下: 打开F盘的Books文件…...
codeshell安装配置
codeshell安装配置 1 注意事项1.1 Python版本问题 2 codeshell环境搭建2.1 codeshell使用软件各版本2.2 软件下载2.3 codeshell使用环境安装2.3.1 python-3.10.9-amd64.exe安装2.3.2 Anaconda3-2022.10-Windows-x86_64.exe安装2.3.3 创建环境2.3.4 Pytorch安装2.3.5 transforme…...

mfc140u.dll丢失的详细解决方法,最详细修复mfc140u.dll丢失的办法分享
在计算机技术日益发展的今天,我们不可避免地会遇到各种各样的技术问题。其中,“MFC140U.DLL丢失”是一个常见的错误,它可能会影响我们的电脑性能和软件运行。本文将详细介绍四种解决“MFC140U.DLL丢失”问题的方法。 首先,我们需…...

CMake
文章目录 前言一、快速开始编译C/C代码1. 只有源码的项目2. 包含库的项目3. 编译成库给他人使用使用cmake的流程1. 生成构建系统2. 执行构建3. 执行测试4. 安装 && 打包 二、cmake 语法简介1 变量2 条件语句3 脚本命令**消息打印****if-else**:**list命令**:…...

互联网Java工程师面试题·Spring篇·第二弹
目录 3、Beans 3.1、什么是 spring bean? 3.2、spring 提供了哪些配置方式? 3.3、spring 支持集中 bean scope? 3.4、spring bean 容器的生命周期是什么样的? 3.5、什么是 spring 的内部 bean? 3.6、什么是 spri…...
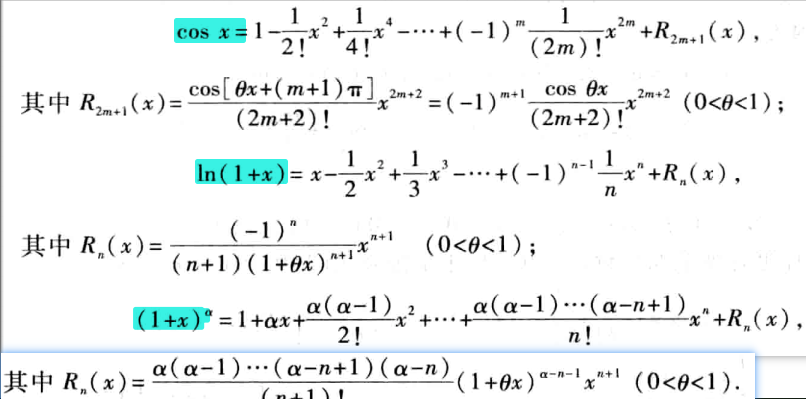
AM@两种余项型泰勒公式的对比和总结@常用函数的麦克劳林公式
文章目录 abstract两种余项型泰勒公式的对比和总结Maclaurin公式常用函数的Maclaurin公式推导例求极限按幂展开 abstract 泰勒公式的两种余项型(Penao&Lagrange)泰勒公式的对比和总结常用的Maclaurin公式列举(Peano余项型为主) 两种余项型泰勒公式的对比和总结 Taylor公式…...

Django实现音乐网站 (22)
使用Python Django框架做一个音乐网站, 本篇音乐播放器功能完善:顺序播放、设置播放数、歌词滚动等功能。 目录 顺序播放 设置顺序播放 单曲播放数 添加路由 视图处理 模板处理 歌词滚动 视图内容返回修改 样式设置 模板内容 歌词滚动脚本 歌…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
