酷开科技 | 酷开系统,为居家生活打开更精彩的窗口
电视在我们的日常生活中扮演着重要的角色。虽然,作为客厅C位的扛把子——电视的娱乐作用深入人心,但是,它的涵义和影响力却因我们每个人的具体生活环境而存在着种种差异,而我们的生活环境又受到我们所处的社会及文化环境的影响。
随着互联网的发展,电视也承载了更多的功能。相比于传统的电视,如今的智能电视屏幕更大、分辨率更高、色彩更加鲜艳,能够呈现出更加逼真的画面效果。当观众观看大屏电视时,仿佛置身于电影大幕的场景之中,感受到更为震撼和刺激的视觉冲击。酷开系统,用电视为你的居家生活打开世界更精彩的窗口。
酷开科技,一直聚焦智能电视系统研发,以内容技术服务和数字营销服务为核心,自主研发的智能电视操作系统——“酷开系统”,打造了业界领跑的智能电视系统运营技术平台,内容涉及影视、购物、游戏、教育、音乐等版块,让消费者通过一台电视轻松掌控更多精彩生活,涵盖生活中的方方面面,简单、便捷、好用、方便。
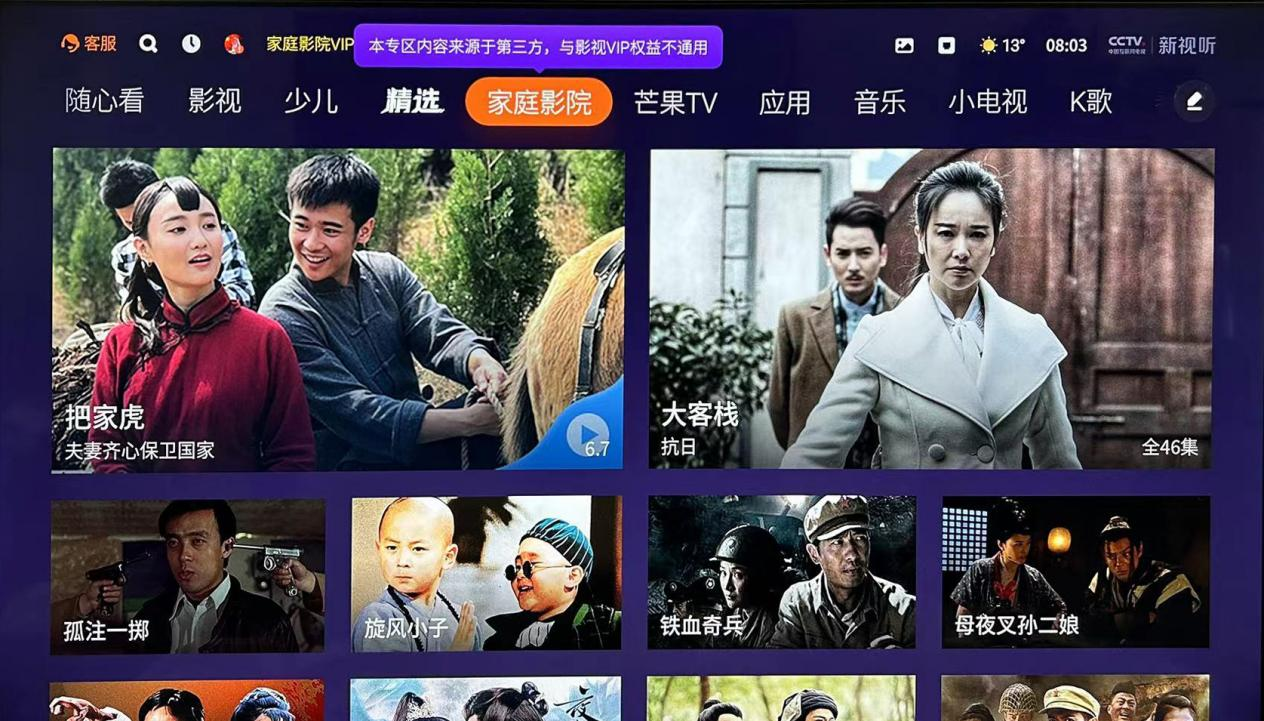
酷开科技还联手腾讯、爱奇艺两大视频巨头,在酷开系统中打造了海量影视库,让精彩不断档。不管是家庭娱乐还是个人放松,在这里都能找到适合的内容!匠心升级5大片库,12个频道,内含万余部电影,上万部电视剧和综艺节目,不管是看综艺、追剧、观影还是刷视频,多种精彩内容倾情奉献,应有尽有,欢乐享不停,分分钟满足消费者的不同需求。
相关文章:

酷开科技 | 酷开系统,为居家生活打开更精彩的窗口
电视在我们的日常生活中扮演着重要的角色。虽然,作为客厅C位的扛把子——电视的娱乐作用深入人心,但是,它的涵义和影响力却因我们每个人的具体生活环境而存在着种种差异,而我们的生活环境又受到我们所处的社会及文化环境的影响。 …...

谷歌真的不喜欢 Node.js ?
有人在 Quora 上提问,为什么谷歌不喜欢 Node.js 呢,Google 的 UX 工程师和来自 Node.js 团队的开发者分别回答了他们对这个问题的看法,对于编程语言来说,每一门语言都有它自己的优势,重要的是如何用它去解决问题。 谷…...

前端项目如何找到所有未被引用的文件
要找到 React 项目中所有未被引用的文件,可以使用工具来进行静态代码分析。以下是一些方法: 使用静态代码分析工具unimported: 静态代码分析工具可以找到未被引用的 JSX 文件。一个常用的工具是 “unimported”。以下是使用它的步骤ÿ…...

CANoe-使用IG Ethernet Packet Builder实现IP包分片的若干问题
在文章《CANoe-Ethernet IG和Ethernet Packet Builder的使用和区别》中,我们讲过Packet Builder可以组装多种类型的以太网报文: 当我们想组装一条icmpv4 echo request报文,payload只有1个字节的数据FF时,选择ICMPv4 Packet,创建一条ICMPv4报文,把payload改为1个字节: 然…...
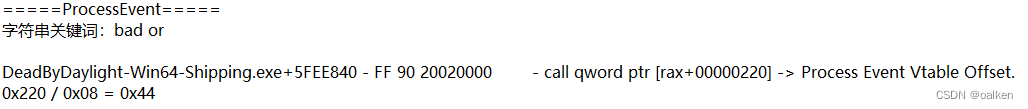
UE4逆向篇-2_各类数据的查找方式
写在前面 1.通过前面的文章,相信各位已经能够自己找到GNames并使用DUMP工具导出GNames了。 2.本篇文章将介绍各种所需数据的查找方法。 一、准备工作 1.CheatEngine,本篇以及后续篇幅的重要工具。 2.一个记事本,保证你能记录下关键信息。…...
)
JDBC-day07(Apache-DBUtils实现CRUD操作)
九:Apache-DBUtils实现CRUD操作 1 Apache-DBUtils简介 Apache-DbUtils 是 Apache 组织提供的开源 JDBC工具类库,它是对JDBC的简单封装,学习成本极低,并且使用DbUtils能极大简化JDBC编码的工作量,同时也不会影响程序的…...
零代码编程:用ChatGPT多线程批量将PDF文档转换为word格式
pdf2docx是Python的一个库,可以很方便的将PDF文档转换为word格式,首先安装这个库。 然后在ChatGPT中输入提示词: 你是一个Python编程专家,要完成一个文档格式转换的任务,具体步骤如下: 打开F盘的Books文件…...
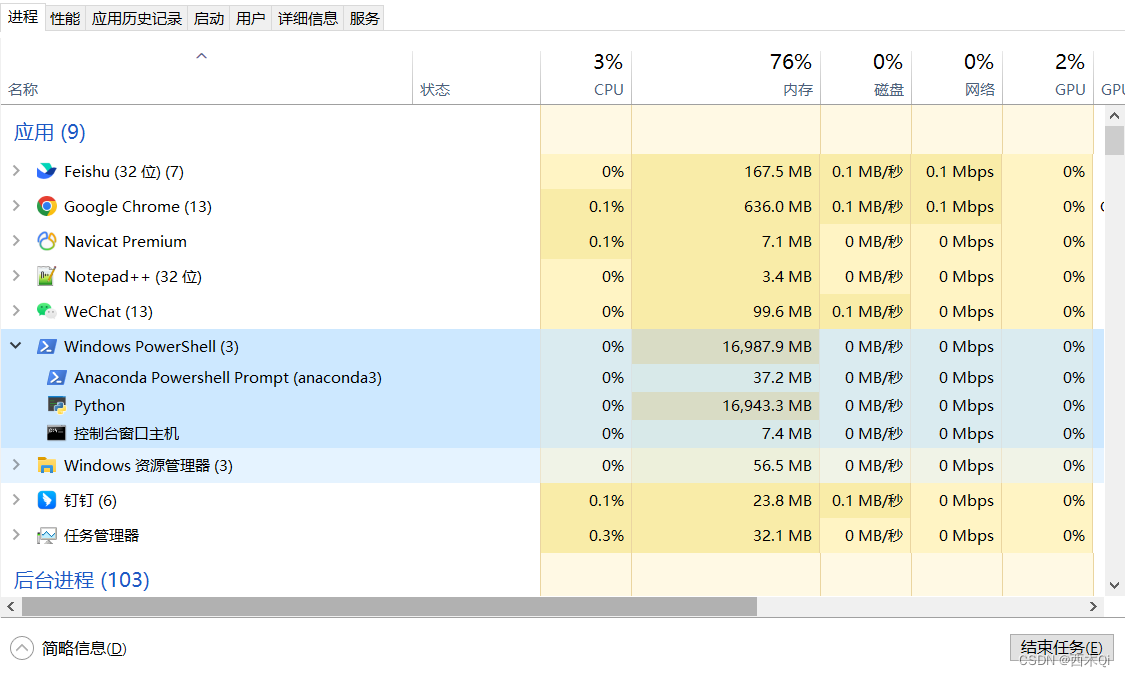
codeshell安装配置
codeshell安装配置 1 注意事项1.1 Python版本问题 2 codeshell环境搭建2.1 codeshell使用软件各版本2.2 软件下载2.3 codeshell使用环境安装2.3.1 python-3.10.9-amd64.exe安装2.3.2 Anaconda3-2022.10-Windows-x86_64.exe安装2.3.3 创建环境2.3.4 Pytorch安装2.3.5 transforme…...

mfc140u.dll丢失的详细解决方法,最详细修复mfc140u.dll丢失的办法分享
在计算机技术日益发展的今天,我们不可避免地会遇到各种各样的技术问题。其中,“MFC140U.DLL丢失”是一个常见的错误,它可能会影响我们的电脑性能和软件运行。本文将详细介绍四种解决“MFC140U.DLL丢失”问题的方法。 首先,我们需…...

CMake
文章目录 前言一、快速开始编译C/C代码1. 只有源码的项目2. 包含库的项目3. 编译成库给他人使用使用cmake的流程1. 生成构建系统2. 执行构建3. 执行测试4. 安装 && 打包 二、cmake 语法简介1 变量2 条件语句3 脚本命令**消息打印****if-else**:**list命令**:…...

互联网Java工程师面试题·Spring篇·第二弹
目录 3、Beans 3.1、什么是 spring bean? 3.2、spring 提供了哪些配置方式? 3.3、spring 支持集中 bean scope? 3.4、spring bean 容器的生命周期是什么样的? 3.5、什么是 spring 的内部 bean? 3.6、什么是 spri…...
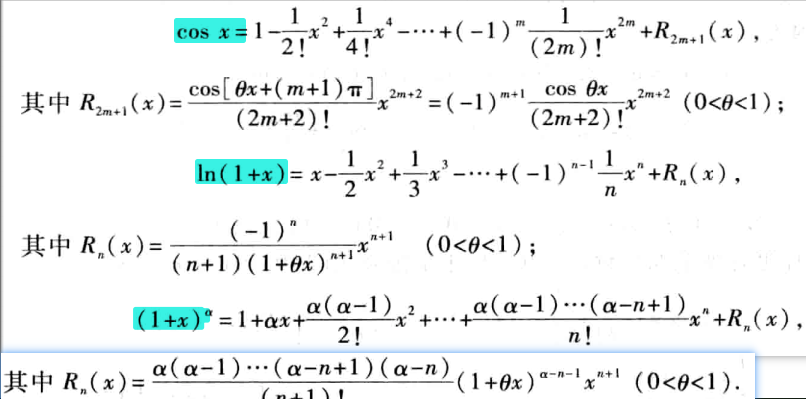
AM@两种余项型泰勒公式的对比和总结@常用函数的麦克劳林公式
文章目录 abstract两种余项型泰勒公式的对比和总结Maclaurin公式常用函数的Maclaurin公式推导例求极限按幂展开 abstract 泰勒公式的两种余项型(Penao&Lagrange)泰勒公式的对比和总结常用的Maclaurin公式列举(Peano余项型为主) 两种余项型泰勒公式的对比和总结 Taylor公式…...

Django实现音乐网站 (22)
使用Python Django框架做一个音乐网站, 本篇音乐播放器功能完善:顺序播放、设置播放数、歌词滚动等功能。 目录 顺序播放 设置顺序播放 单曲播放数 添加路由 视图处理 模板处理 歌词滚动 视图内容返回修改 样式设置 模板内容 歌词滚动脚本 歌…...

pnpm ERR_PNPM_ADDING_TO_ROOT
ERR_PNPM_ADDING_TO_ROOT Running this command will add the dependency to the workspace root, which might not be what you want - if you really meant it, make it explicit by running this command again with the -w flag (or --workspace-root). If you don’t wa…...

统计学习方法 拉格朗日对偶性
文章目录 统计学习方法 拉格朗日对偶性原始问题对偶问题原始问题和对偶问题的关系 统计学习方法 拉格朗日对偶性 读李航的《统计学习方法》时,关于拉格朗日对偶性的笔记。 在许多统计学习的约束最优化问题中,例如最大熵模型和支持向量机,常…...
.rancher-pipeline.yml
一、注意点 其实下文二的image是基于这个镜像作为基础镜像在这个镜像中执行打包,shellScript 当前路径是你代码块与上图settings.xml,图中的settings.xml可以替换下你当前镜像的settings.xml 示例 二、.rancher-pipeline.yml ${CICD_GIT_BRANCH}这些从官…...
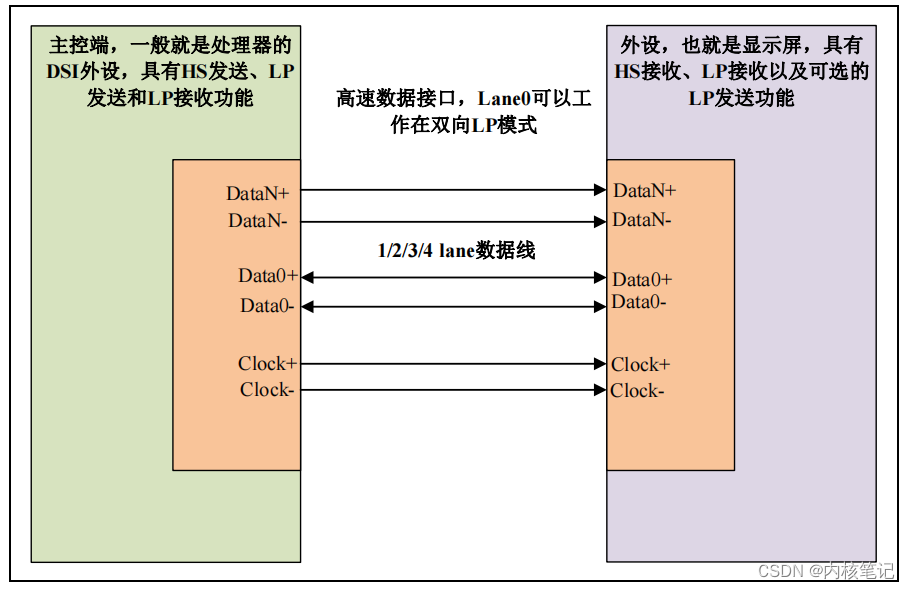
RK3588平台开发系列讲解(显示篇)MIPI DSI协议介绍之分层
🚀返回专栏总目录 文章目录 一、MIPI DSI 分层1.1、应用层1.2、协议层1.3、链路层1.4、物理层沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 DSI 全称是 Display Serial Interface,是主控和显示模组之间的串行连接接口。 MIPI DSI 接口分为数据线和时钟线,均为…...

前端学成在线项目详细解析三
19-推荐课程-内容样式 HTML结构 <ul><li><a href"#"><div class"pic"><img src"./uploads/course01.png" alt""></div><div class"text"><h4>JavaScript数据看板项目实战…...
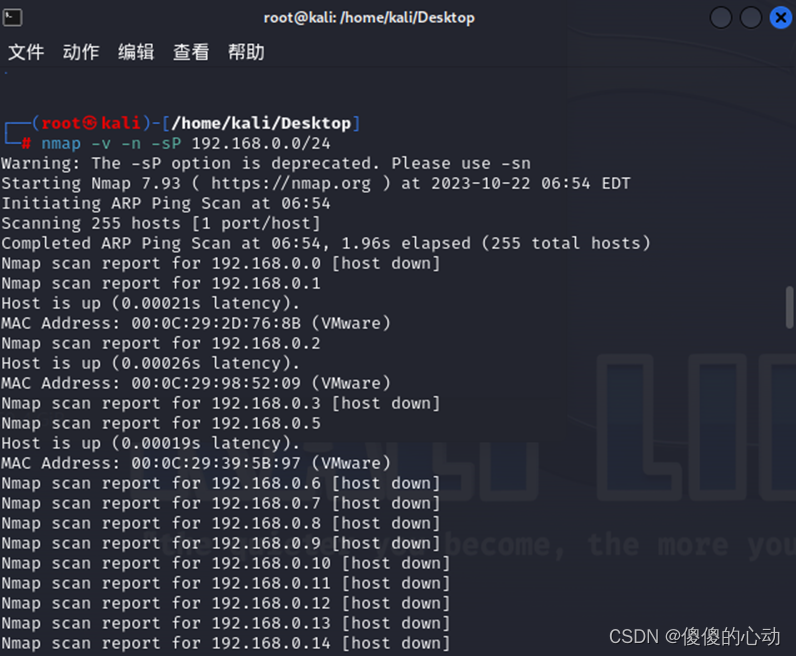
使用Kali进行实验---主机发现
主机发现 【实训目的】 掌握主机扫描的工作原理,学会使用ping等扫描工具,发现网络当中活跃的主机。 【场景描述】 在虚拟机环境下配置4个虚拟系统“Win XP1” “Win XP2” “Kali Linux”和“Metasploitable2”,使得4个系统之间能够相互通…...
)
美团笔试真题2023第一场(4题)
点评: 题目总体来说偏向于中下难度 1.字符串前缀 题目描述: 现在有两个字符串S和T,你需要对S进行若干次操作,使得S是T的一个前缀(空串也是一个前缀)。每次操作可以修改S的一个字符,或者删除一个…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
